文档内容
高二开学考数学
一、单选题(每小题5分,共40分)
1. 样本数据24,13,14,18,12,14,20,16的75%分位数为( )
A. 17 B. 18 C. 19 D. 20
【答案】C
【解析】
【分析】由百分位数的定义即可得解.
【详解】数据从小到大排序为12,13,14,14,16,18,20,24,则 ,
所以75%分位数为 .
故选:C.
2. 设事件A,B,已知P(A)= ,P(B)= ,P(A∪B)= ,则A,B之间 的关系一定为( )
.
A 两个任意事件 B. 互斥事件
C. 非互斥事件 D. 对立事件
【答案】B
【解析】
【分析】由题意先求P(A)+P(B),然后检验P(A)+P(B)是否与P(A∪B)相等,从而可判断是否
满足互斥关系
【详解】因为P(A)+P(B)= =P(A∪B),所以A,B之间的关系一定为互斥事件.
故选:B
【点睛】此题考查了互斥事件的概率公式的简单应用,属于基础题
3. 某圆台上底面圆半径为1,下底面圆半径为2,母线长为 ,则该圆台的体积为( )
A. B. C. D.
【答案】A
【解析】
【分析】先求出圆台的高,再由圆台的体积公式求出即可.
第1页/共21页
学科网(北京)股份有限公司【详解】设圆台的母线长为l,高为h,
因为圆台上底面圆的半径 为1,下底面圆半径 为2,母线 ,
因此圆台的高为 ,
所以圆台的体积为 .
故选:A
4. 已知向量 , 满足 , ,且 , 的夹角为 ,则向量 在向量 方向上的投影向量为
( )
A. B. C. D.
【答案】D
【解析】
【分析】利用投影向量的公式即可求解.
【详解】向量 在向量 方向上的投影向量 ,
故选:D.
5. 已知非零向量 满足 ,且向量 在向量 上的投影向量为 ,则 与 的夹角为( )
A. B. C. D.
【答案】C
【解析】
【分析】由投影向量计算可得.
【详解】因为 ,且 ,
所以 ,即夹角为 ,
第2页/共21页
学科网(北京)股份有限公司故选:C.
6. 在 中,内角 的对边分别为 ,且 ,则 的最大值
是( )
A. B. C. D.
【答案】D
【解析】
【分析】利用正弦定理、余弦定理进行角化边整理得到 ,再通过余弦定理消元得到
,然后利用基本不等式得出 的最小值,从而可以得到 的最大值.
【详解】因为 ,
由正弦定理得 ,
所以 ,
所以 ,
由余弦定理得 ,
,
当且仅当 ,即 时,等号成立,
第3页/共21页
学科网(北京)股份有限公司所以 ,
所以当 时, 取得最大值,
此时 ,
所以 的最大值是 .
故选:D.
7. 已知函数 ,若对任意的实数 , 在区间 上的值域
均为 ,则 的取值范围为( )
A. B. C. D.
【答案】D
【解析】
【分析】根据三角恒等变换化简函数解析式,再根据余弦型函数的值域与周期性可得解.
【详解】由 ,
函数值域为 ,
又对任意的实数 , 在区间 上的值域均为 ,
则 ,
解得 ,
故选:D.
第4页/共21页
学科网(北京)股份有限公司8. 某高校的入学面试中有3道难度相当的题目,李华答对每道题目的概率都是 ,若每位面试者共有三次
机会,一旦某次答对抽到的题目,则面试通过,否则就一直抽题到第3次为止,假设对抽到的不同题目能
否答对是独立的,则李华最终通过面试的概率为( )
A. B. C. D.
【答案】D
【解析】
【分析】利用相互独立事件及对立事件的概率公式计算即得.
【详解】依题意,李华3道题都没有答对的概率为 ,
所以李华最终通过面试的概率为 .
故选:D
二、多选题(本题共3小题,每小题6分,共18分,在每小题给出的选项中,有多项符合题
目要求,全部选对的得6分,部分选对的得部分分,有选错的得0分)
9. 已知平面向量 , ,则( )
A. 当 时, B. 若 ,则
C. 若 ,则 D. 若 与 的夹角为钝角,则
【答案】ACD
【解析】
【分析】根据向量加法坐标公式计算可判断A;根据向量平行的坐标公式计算即可判断 B;根据向量垂直
坐标公式计算即可判断C;根据向量数量积坐标公式计算即可判断D.
【详解】对A,当 时, ,所以 ,故A正确;
第5页/共21页
学科网(北京)股份有限公司对B,若 ,则 ,解得 ,故B错误;
对C,若 ,则 ,解得 ,故C正确;
对D,若 与 的夹角为钝角,则 且 与 不共线,
解得 且 ,即 ,故D正确,
故选:ACD
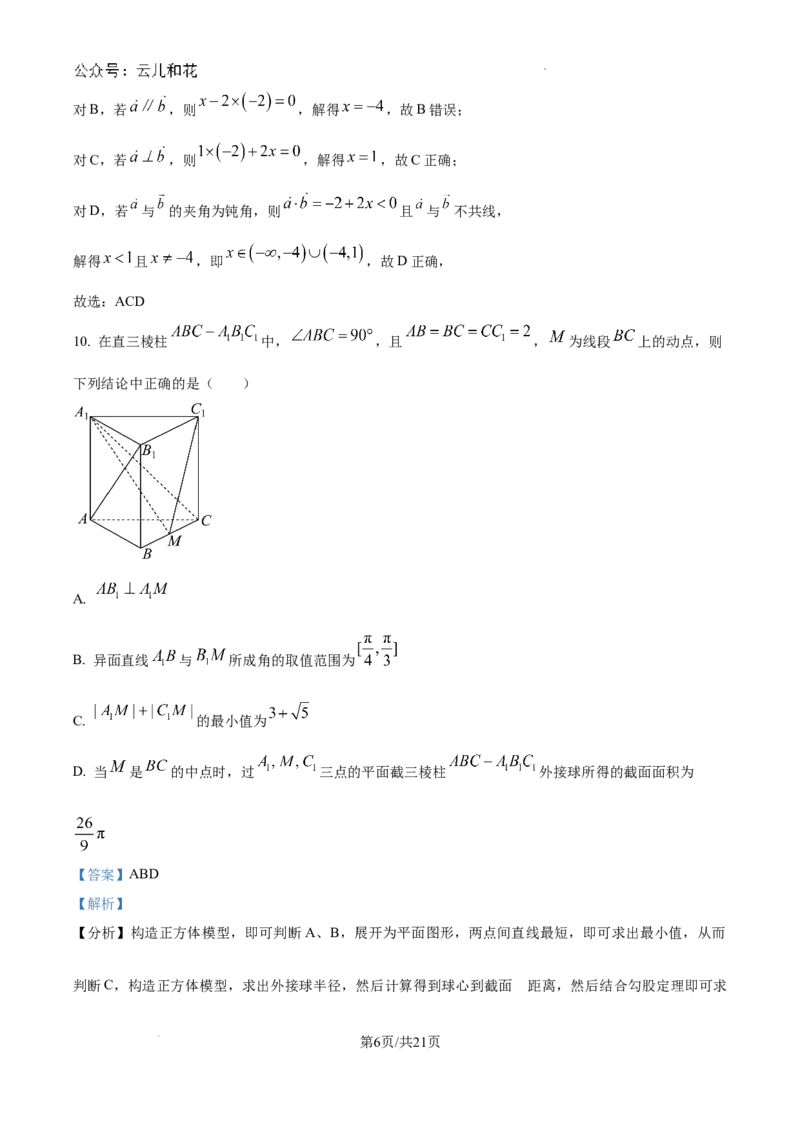
10. 在直三棱柱 中, ,且 , 为线段 上的动点,则
下列结论中正确的是( )
A.
B. 异面直线 与 所成角的取值范围为
C. 的最小值为
D. 当 是 的中点时,过 三点的平面截三棱柱 外接球所得的截面面积为
【答案】ABD
【解析】
【分析】构造正方体模型,即可判断A、B,展开为平面图形,两点间直线最短,即可求出最小值,从而
的
判断C,构造正方体模型,求出外接球半径,然后计算得到球心到截面 距离,然后结合勾股定理即可求
第6页/共21页
学科网(北京)股份有限公司解D选项.
【详解】
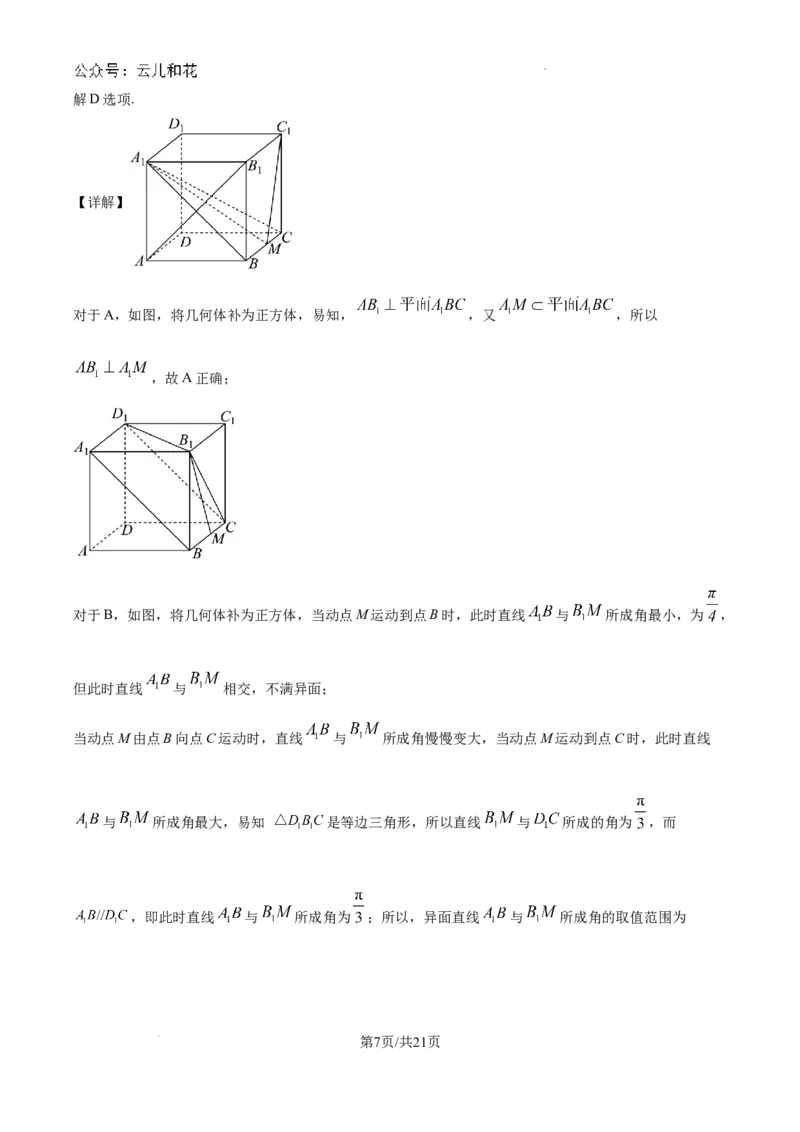
对于A,如图,将几何体补为正方体,易知, ,又 ,所以
,故A正确;
对于B,如图,将几何体补为正方体,当动点M运动到点B时,此时直线 与 所成角最小,为 ,
但此时直线 与 相交,不满异面;
当动点M由点B向点C运动时,直线 与 所成角慢慢变大,当动点M运动到点C时,此时直线
与 所成角最大,易知 是等边三角形,所以直线 与 所成的角为 ,而
,即此时直线 与 所成角为 ;所以,异面直线 与 所成角的取值范围为
第7页/共21页
学科网(北京)股份有限公司,故B错误;
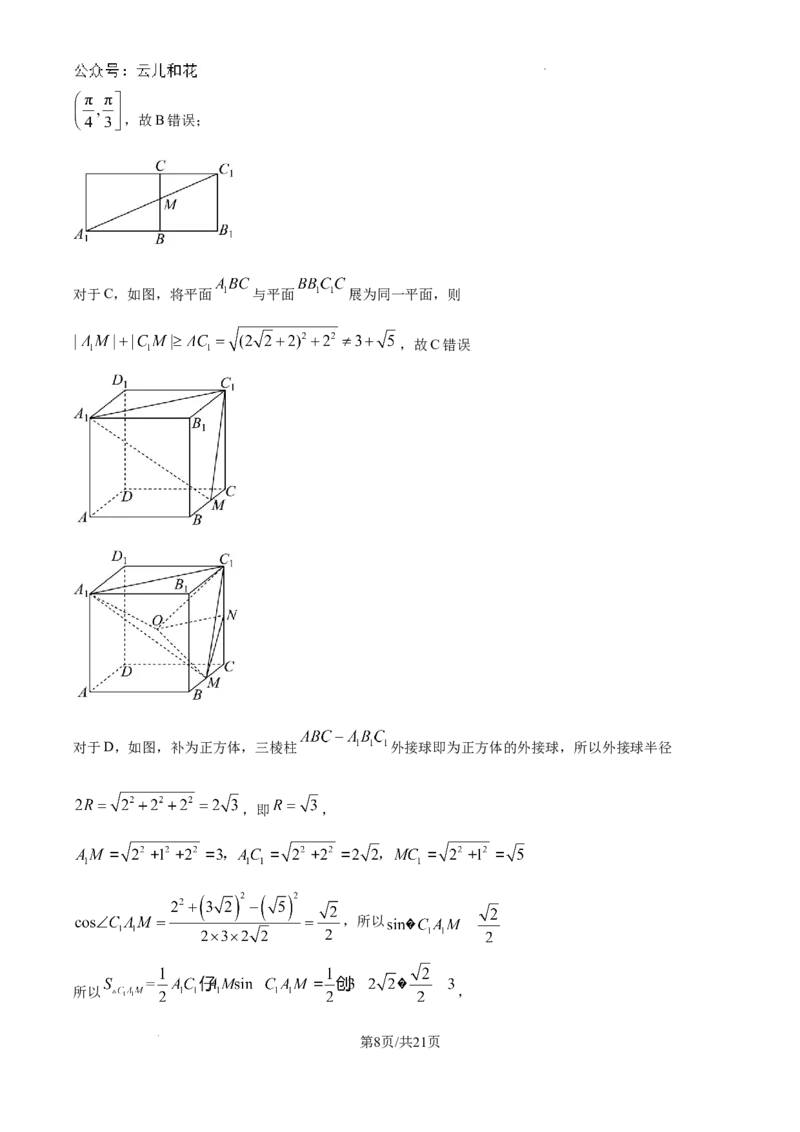
对于C,如图,将平面 与平面 展为同一平面,则
,故C错误
对于D,如图,补为正方体,三棱柱 外接球即为正方体的外接球,所以外接球半径
,即 ,
,所以
所以 ,
第8页/共21页
学科网(北京)股份有限公司取正方体的中心点O, 的中点N,连接ON,易知 ,
所以 ,设正方体的中心点O到截面 的距离为h,
即球心到截面的距离为 ,根据勾股定理可得截面圆半径为 ,
所以截面面积为 ,故D正确.
故选:AD
11. 设 为随机事件,且 ,下列说法正确的是( )
A. 事件 相互独立与 互斥不可能同时成立
B. 若三个事件 两两独立,则
C. 若事件 独立,则
D. 若 ,则
【答案】ACD
【解析】
【分析】利用相互独立性的性质,相互独立事件是可以同时发生的,而互斥事件是不可能同时发生的;三
个事件两两独立,不能确定三个事件相互独立,即不能判断 是否成立;利用
概率公式 求解.
【详解】若 相互独立,则 ;若 互斥,则 ,
而 , ,所以事件 相互独立与 互斥不可能同时成立,故A正确;
第9页/共21页
学科网(北京)股份有限公司当三个事件 两两独立时, 一般不成立.
比如:设样本空间 含有等可能的样本点,且 ,
则 , ,
所以 ,
即三个事件 两两独立,但是 ,故B错误;
若 相互独立,则 也独立,故C正确;
由 得 ,所以 ,故D正确;
故选:ACD.
三、填空题
12. 已知平面向量 ,向量 在向量 上的投影向量为 ,则 =______.
【答案】
【解析】
【分析】根据投影向量的定义即可求解
【详解】由投影向量的定理可得,向量 在向量 上的投影向量为: ,
又向量 在向量 上的投影向量为 ,所以 ,
所以 ,所以 ,
第10页/共21页
学科网(北京)股份有限公司故答案为:
13. 已知事件 与 相互独立, , ,则 ______.
【答案】0.88
【解析】
【分析】根据独立事件乘法公式求出 ,从而利用 求出答案.
【详解】因为事件 与 相互独立,
所以 ,
所以 .
故答案为:0.88
的
14. 已知四面体 中,棱BC,AD所在直线所成 角为 ,且 , ,
,则四面体 体积的最大值是__________.
【答案】
【解析】
【分析】作出辅助线,找到 ,求出 ,由正弦定理得到点 在半径为 的
的外接圆的劣弧 上,当平面 ⊥平面 时,点 到平面 的距离最大,且最大距离
为 ,从而求出三棱锥 的体积最大值为 ,由 得到答案.
【详解】在平面 内,分别过 作 的平行线交于点 ,连接 ,
则四边形 为平行四边形,则 , ,
则 ,
第11页/共21页
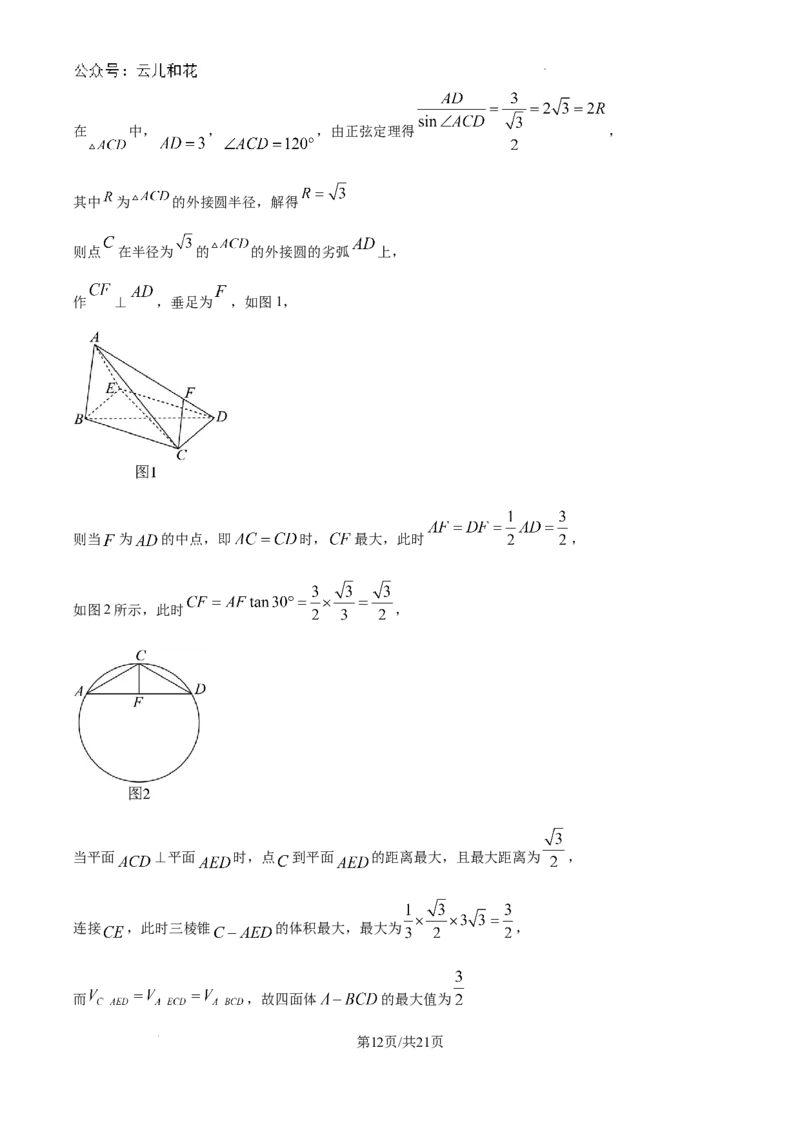
学科网(北京)股份有限公司在 中, , ,由正弦定理得 ,
其中 为 的外接圆半径,解得
则点 在半径为 的 的外接圆的劣弧 上,
作 ⊥ ,垂足为 ,如图1,
则当 为 的中点,即 时, 最大,此时 ,
如图2所示,此时 ,
当平面 ⊥平面 时,点 到平面 的距离最大,且最大距离为 ,
连接 ,此时三棱锥 的体积最大,最大为 ,
而 ,故四面体 的最大值为
第12页/共21页
学科网(北京)股份有限公司故答案为:
【点睛】关键点点睛,将四面体 补形为四棱锥,从而结合异面直线夹角求出三角形面积,再结
合点到平面的距离最大值求出体积最大值
四、解答题:本题共5小题,第15小题13分,第16、17小题15分,第18、19小题17分,共
77分.解答应写出文字说明、证明过程或演算步骤.
15. 抛掷两枚质地均匀的骰子(标号为 号和 号),记下两枚骰子朝上的点数,求下列事件的概率:
(1) “两个点数之和是5”;
(2) “两个点数相等”;
(3) “ 号骰子的点数大于 号骰子的点数”.
【答案】(1)
(2)
(3)
【解析】
的
【分析】(1)判断出符合古典概型,列出样本空间,找到满足事件 样本点,求比值即可;
(2)列出满足事件 的样本点,求比值即可;
(3)列出满足事件 的样本点,求比值即可.
【小问1详解】
用 表示 号出现的点数为 ,用 表示 号出现的点数为 ,
则用 表示这个实验的一个样本点,
样本空间 ,共有36个样本点.
由于骰子的质地均匀,所有各个样本点出现的可能性相等,因此这个试验是古典概型.
第13页/共21页
学科网(北京)股份有限公司,
,
;
【小问2详解】
,
,
;
【小问3详解】
.
16. 已知平面向量 , , ,且 , .
(1)求 和 ;
(2)若 , ,求向量 和向量 的夹角的大小.
【答案】(1) , ;
(2) .
【解析】
【分析】(1)由 列方程可求出 ,再由 列方程可求出 ,从而可求出 和 ;
第14页/共21页
学科网(北京)股份有限公司(2)先求出向量 和向量 的坐标,再利用向量的夹角公式求解即可.
【小问1详解】
因为 ,所以 ,解得 ,
因为 ,所以 ,解得 ,
故 , ;
【小问2详解】
, ,
设向量 和向量 的夹角为 ,
则 ,
因为 ,所以 ,
即向量 和向量 的夹角的大小为 .
17. 在 中,内角A,B,C的对边分别为 ,且 .
(1)求角 ;
(2)若 ,求 面积的最大值.
【答案】(1)
(2)
【解析】
【分析】(1)依据给定条件,并结合正弦定理,余弦定理求解即可.
(2)利用重要不等式求出 ,再结合三角形面积公式求解即可.
第15页/共21页
学科网(北京)股份有限公司【小问1详解】
在 中,若 ,
由正弦定理得 ,故 ,
即 ,由余弦定理得 ,故
【小问2详解】
当 时, ,由重要不等式得 ,
当且仅当 时取等,故有 ,解得 ,
而 ,故 ,
故 面积的最大值是 .
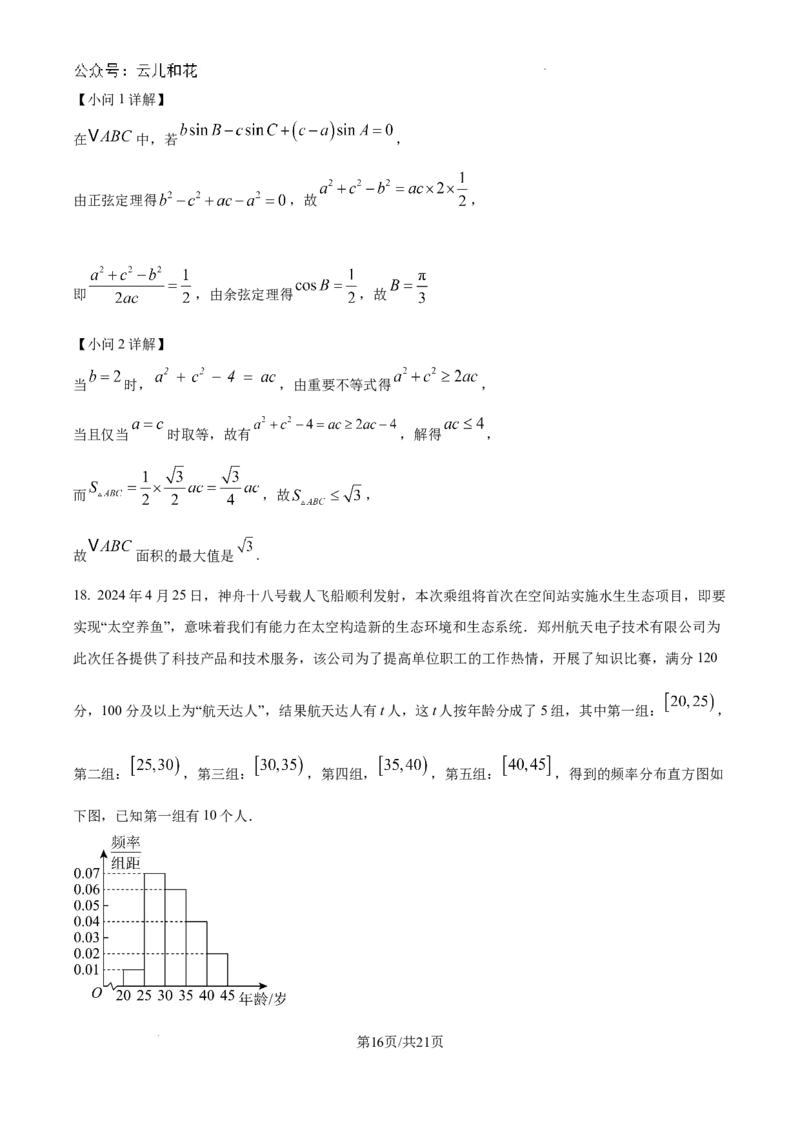
18. 2024年4月25日,神舟十八号载人飞船顺利发射,本次乘组将首次在空间站实施水生生态项目,即要
实现“太空养鱼”,意味着我们有能力在太空构造新的生态环境和生态系统.郑州航天电子技术有限公司为
此次任各提供了科技产品和技术服务,该公司为了提高单位职工的工作热情,开展了知识比赛,满分120
分,100分及以上为“航天达人”,结果航天达人有t人,这t人按年龄分成了5组,其中第一组: ,
第二组: ,第三组: ,第四组, ,第五组: ,得到的频率分布直方图如
下图,已知第一组有10个人.
第16页/共21页
学科网(北京)股份有限公司(1)根据频率分布直方图,估计这t人年龄的第80百分位数;
(2)现从以上各组中用分层随机抽样的方法抽取20人,担任“航天工程”的宣传大使.若第四组宣传大使
的年龄的平均数与方差分别为36和 ,第五组宣传大使的年龄的平均数与方差分别为42和1,据此估计
这t人中35~45岁所有人的年龄的平均数和方差.(分层随机抽样中各层抽取的样本量、样本平均数和样
本方差分别为:m, , ,n, , .记总体的样本平均数为 ,样本方差为 ,则
,
【答案】(1)
(2)年龄的平均数为 ,方差约为
【解析】
【分析】(1)根据频率分布直方图可确定第 百分位数第四组,根据第 百分位数定义可构造方程求得
结果;
(2)由 可求得第四组和第五组所有宣传使者的年龄平均数,由
可求得第四组和第五组所有宣传使者的年龄方差.
【小问1详解】
设第 百分位数为 ,
, ,
位于第四组: 内;
由 得: .
【小问2详解】
第17页/共21页
学科网(北京)股份有限公司由题意得,第四组应抽取 人;第五组抽取 人, 设第四组的宣传使者的
年龄分别为 ,平均数分别为 ,方差分别为 ,
设第五组的宣传使者的年龄分别为 , ,平均数分别为 ,方差分别为 ,
设第四组和第五组所有宣传使者的年龄平均数为 ,方差为 .
则 ,
即第四组和第五组所有宣传使者的年龄平均数为 ,
则
.
即第四组和第五组所有宣传使者的年龄方差为 ;
据此估计这 人中年龄在 岁的所有人的年龄的平均数为 ,方差约为 .
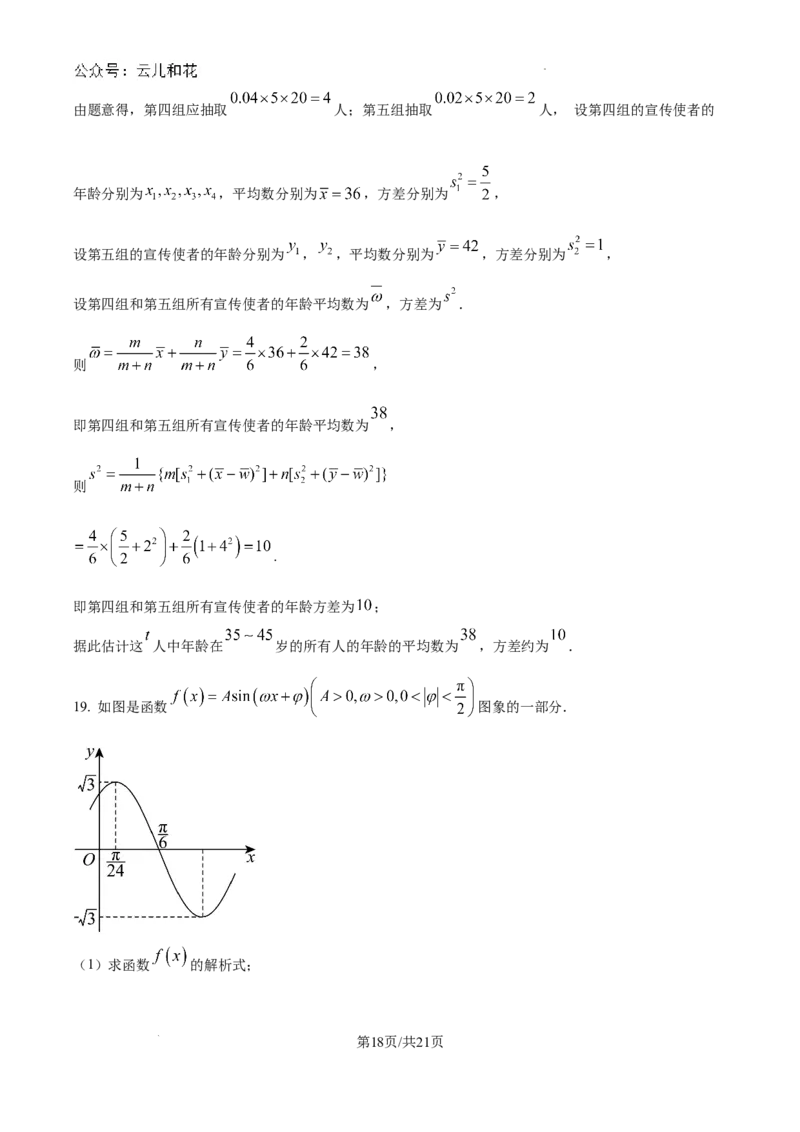
19. 如图是函数 图象的一部分.
(1)求函数 的解析式;
第18页/共21页
学科网(北京)股份有限公司(2)求函数 的单调区间;
(3)记方程 在 上的根从小到大依次为 ,若
,试求 与 的值.
【答案】(1)
(2)单调递增区间为 , ,单调递减区间为 ,
(3) ,
【解析】
【分析】(1)根据函数图象可得 ,由周期求出 ,再根据函数过点 求出 ,即可得到函数
解析式;
(2)根据正弦函数的性质计算可得;
(3)依题意可得 ,由 的取值范围求出 的取值范围,令 ,
,即 ,结合正弦函数的图象及对称性计算可得.
【小问1详解】
由图可得 ,
函数 的最小正周期为 ,又 ,
则 ,所以 ,
第19页/共21页
学科网(北京)股份有限公司又函数过点 ,所以 ,则 ,
则 ,解得 ,
因为 ,所以 ,
所以 .
【小问2详解】
令 , ,解得 , ,
令 , ,解得 , .
因此函数 的单调递增区间为 , ,单调递减区间为 , .
【小问3详解】
方程 ,即 ,即 ,
因为 ,所以 ,
设 ,其中 ,即 ,
结合正弦函数 的图象,可得方程 在区间 有 个解,即 ,
又 的对称轴为 ,
不妨设 个解从小到大依次为 ,
第20页/共21页
学科网(北京)股份有限公司则 关于 对称, 关于 对称, 关于 对称,
所以 , , ,
即 , , ,
解得 , , .
所以 ,
所以 , .
【点睛】关键点点睛:本题第三问关键是换元转化为方程 在区间 上的解的个数,结合
正弦函数的图象及对称性计算得解.
第21页/共21页
学科网(北京)股份有限公司