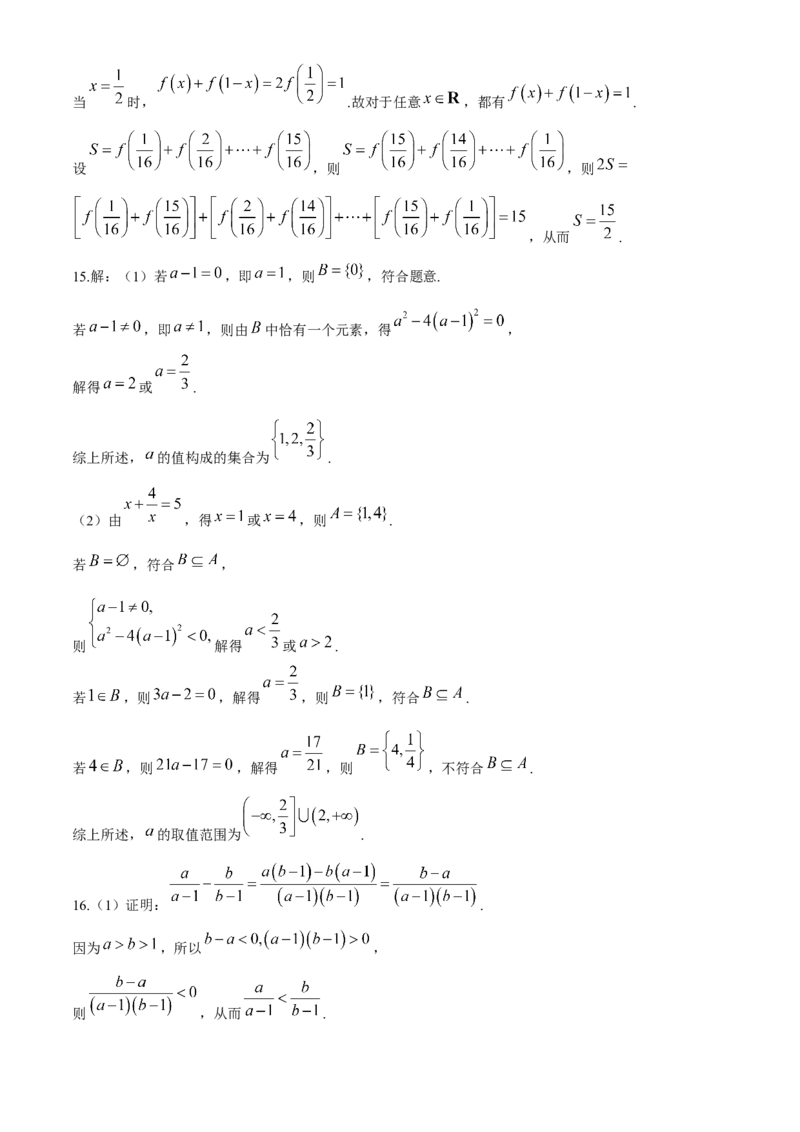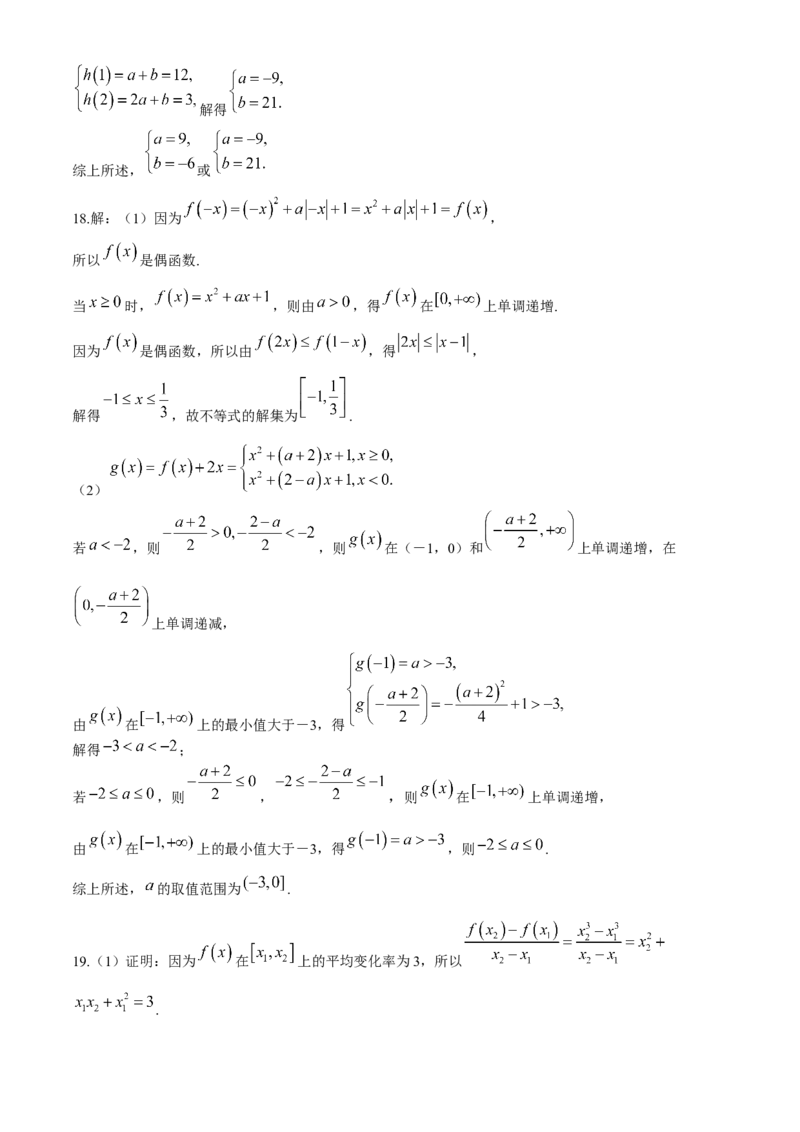文档内容
2024~2025 学年度第一学期期中重点校联考
高二数学
出题校:芦台一中 宝坻一中
一、选择题(本题共9小题,每题5分,共45分)
1.已知直线 的倾斜角为 ,且经过点 ,则直线 的方程为( ).
A. B. C. D.
2.在空间直角坐标系 中,点 关于 轴对称点的坐标为( ).
A. B. C. D.
3.方程 表示椭圆的充要条件是( ).
A. B. 或
C. D.
4.若直线 与 平行,则 的值为( ).
A.0 B.2 C.3 D.2或3
5.已知两点 , ,过点 的直线 与线段 (含端点)有交点,则直线 的斜率的
取值范围为( ).
A. B.
C. D.
6.已知圆 ,若直线 与圆 相交于A,B两点,则 的最小值
为( ).
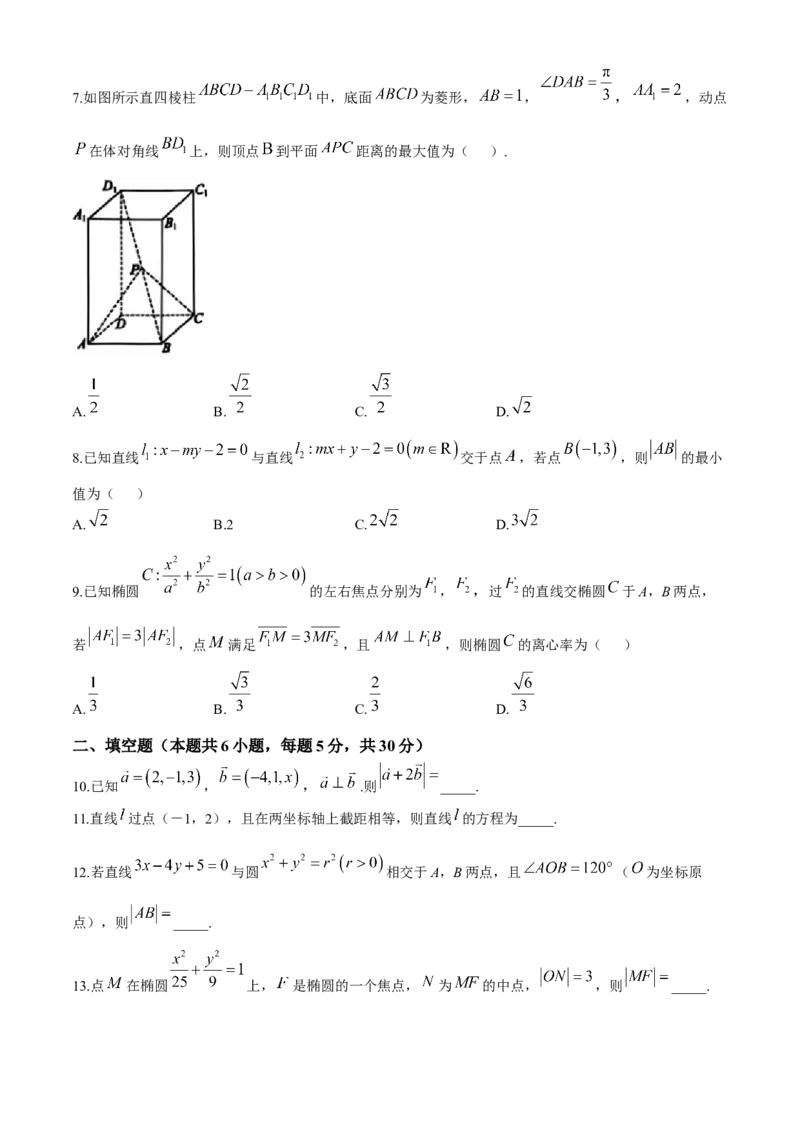
A. B. C. D.37.如图所示直四棱柱 中,底面 为菱形, , , ,动点
在体对角线 上,则顶点 到平面 距离的最大值为( ).
A. B. C. D.
8.已知直线 与直线 交于点 ,若点 ,则 的最小
值为( )
A. B.2 C. D.
9.已知椭圆 的左右焦点分别为 , ,过 的直线交椭圆 于A,B两点,
若 ,点 满足 ,且 ,则椭圆 的离心率为( )
A. B. C. D.
二、填空题(本题共6小题,每题5分,共30分)
10.已知 , , .则 _____.
11.直线 过点(-1,2),且在两坐标轴上截距相等,则直线 的方程为_____.
12.若直线 与圆 相交于A,B两点,且 ( 为坐标原
点),则 _____.
13.点 在椭圆 上, 是椭圆的一个焦点, 为 的中点, ,则 _____.14.已知圆 和两点 , ,若圆 上存在点 ,使得
,则 的最小值为_____.
15.已知 是椭圆 上一点, , 是 的两个焦点, ,点 在
的平分线上, 为原点, ,且 .则 的离心率为_____.
三、解答题(本题共75分)
16.(14分)直线 过点 且与直线 垂直.
(1)求直线 的方程;
(2)求圆心在直线 上且过点 、 的圆的方程.
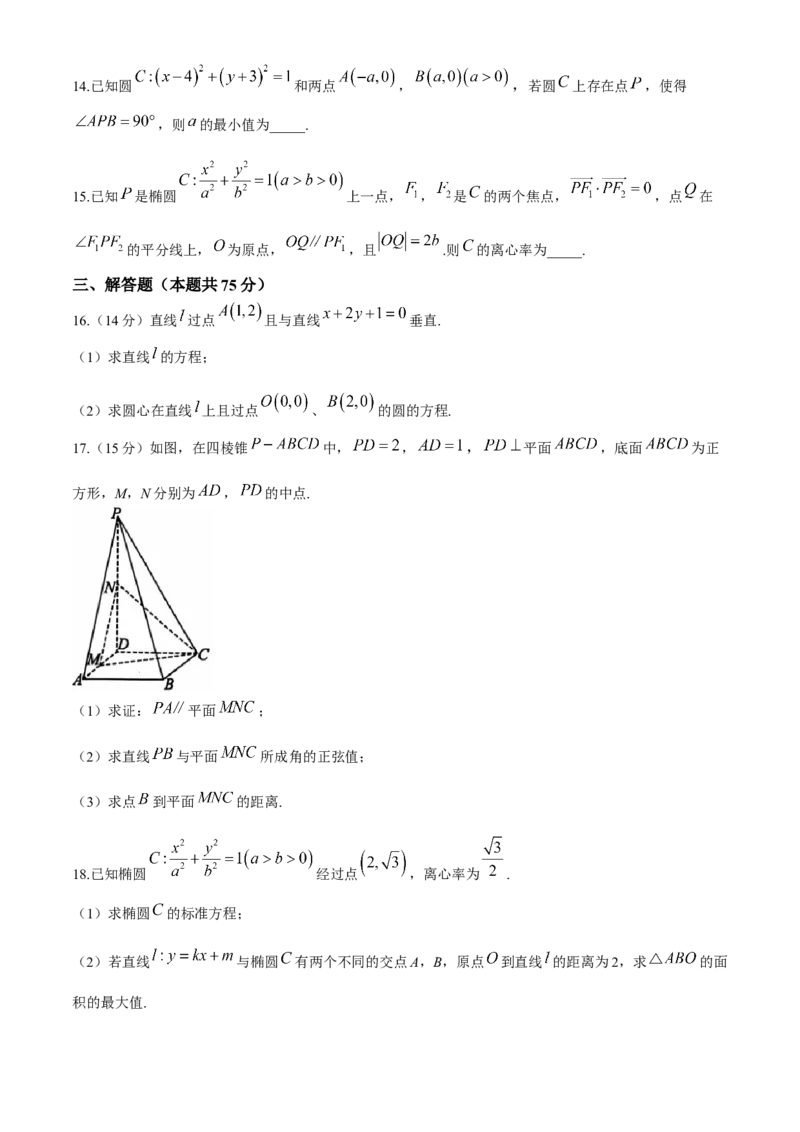
17.(15分)如图,在四棱锥 中, , , 平面 ,底面 为正
方形,M,N分别为 , 的中点.
(1)求证: 平面 ;
(2)求直线 与平面 所成角的正弦值;
(3)求点 到平面 的距离.
18.已知椭圆 经过点 ,离心率为 .
(1)求椭圆 的标准方程;
(2)若直线 与椭圆 有两个不同的交点A,B,原点 到直线 的距离为2,求 的面
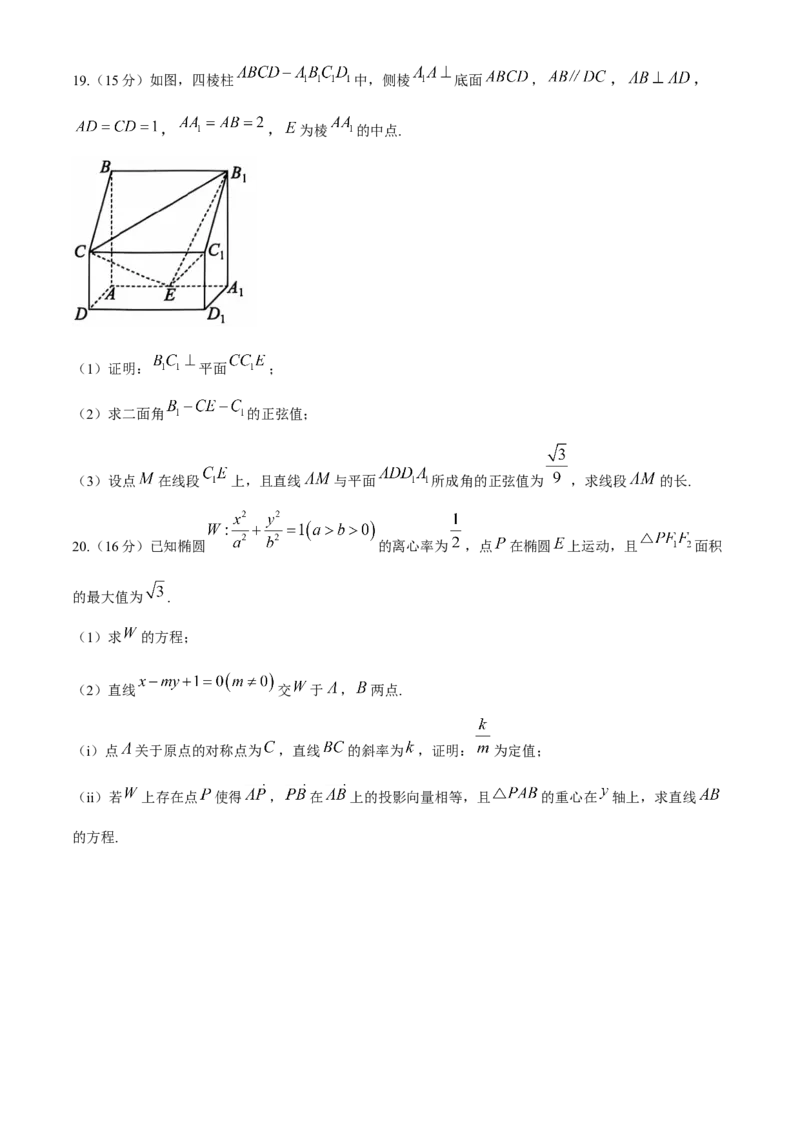
积的最大值.19.(15分)如图,四棱柱 中,侧棱 底面 , , ,
, , 为棱 的中点.
(1)证明: 平面 ;
(2)求二面角 的正弦值;
(3)设点 在线段 上,且直线 与平面 所成角的正弦值为 ,求线段 的长.
20.(16分)已知椭圆 的离心率为 ,点 在椭圆 上运动,且 面积
的最大值为 .
(1)求 的方程;
(2)直线 交 于 , 两点.
(i)点 关于原点的对称点为 ,直线 的斜率为 ,证明: 为定值;
(ii)若 上存在点 使得 , 在 上的投影向量相等,且 的重心在 轴上,求直线
的方程.2024-2025 年度上学期高一年级期中考试
数学参考答案
1.C因为 , ,所以 .
2.C因为 是幂函数,所以 ,得 ,则 , .
3.A由 ,得 或 ,故“ ”是“ ”的充分不必要条件.
4.B设 ,则由 ,得 ,即
,则 得 则 , .
5.D设每束鲜花的售价降低 元,则花店该品种鲜花的日销售额
,故当 ,即每束鲜花的售价为34元时,花店该品种鲜花的日
销售额最大.
6.C由题可知 的定义域为 ,且 ,所以 是奇函数,
排除A,B.当 时, ,排除D.故选C.
7.B因为 的定义域为 ,所以在 中, ,则 ,则在
中, ,则 .又 ,所以 的定义域为 .
2a5
b
a1
8.A由 ,得 ,则
,当且仅当 时,等号成立.
9.ABC空集是任何集合的子集,A正确.“有些三角形是等腰三角形”的否定为“所有的三角形都不是等腰
三角形”,B正确.若 ,则 ,当且仅当 时,等号成立,故“ ”是“ ”的一个充分条件,C正确.取 ,则 , ,
D不正确.
10.ACD因为关于 的不等式 的解集为(1,2),所以 整理得
则 .由 ,解得
.由 ,解得 ,则 .故选ACD.
11.AC由 ,得 ,则
,整理得 .令函数 ,则
由 ,得 ,从而 在 上单调递增,则 ,即
,即 ,A正确,B不正确.因为 ,
所以 ,则 ,即 ,C正确. 与 的大小
关系不确定,D不正确.
12.-2若 则 或 当 时, ,此时 ;当
时, ,不符合集合元素的互异性.若 则 不符合集合元素的互异性.
13.(-5,4)因为 ,所以 ,则 .
14. 当 时, , .当 时, .故对于任意 ,都有 .
设 ,则 ,则
,从而 .
15.解:(1)若 ,即 ,则 ,符合题意.
若 ,即 ,则由 中恰有一个元素,得 ,
解得 或 .
综上所述, 的值构成的集合为 .
(2)由 ,得 或 ,则 .
若 ,符合 ,
则 解得 或 .
若 ,则 ,解得 ,则 ,符合 .
若 ,则 ,解得 ,则 ,不符合 .
综上所述, 的取值范围为 .
16.(1)证明: .
因为 ,所以 ,
则 ,从而 .(2)解:因为 ,所以
.
因为 ,所以 ,
当且仅当 , 时,等号成立,
故 的最小值为 .
17.解:(1)因为 与 分别是定义在 上的奇函数、偶函数,所以 ,
.
由 ①,得
,
则 ②.
①-②得 ,则
从而 .
(2)因为 与 均是增函数,所以 也是增函数.又 ,所以 在
上的值域为 .
若 ,则 在 上单调递增.因为 与 在 上的值域相同,所以
解得
若 ,则 为常数函数,显然不符合题意.
若 ,则 在 上单调递减.因为 与 在 上的值域相同,所以解得
综上所述, 或
18.解:(1)因为 ,
所以 是偶函数.
当 时, ,则由 ,得 在 上单调递增.
因为 是偶函数,所以由 ,得 ,
解得 ,故不等式的解集为 .
(2)
若 ,则 ,则 在(-1,0)和 上单调递增,在
上单调递减,
由 在 上的最小值大于-3,得
解得 ;
若 ,则 , ,则 在 上单调递增,
由 在 上的最小值大于-3,得 ,则 .
综上所述, 的取值范围为 .
19.(1)证明:因为 在 上的平均变化率为3,所以
.由 ,得 ,
从而 ,则 .
(2)①证明:因为 ,所以 .
又 ,所以 ,
则 ,从而 .
,
因为 ,所以 ,则 ,即 .
又 ,所以 ,即 .
②解:任取 ,则 ,即
,所以 在(0,1)上单调递减,由 ,得 .
因为 ,所以 ,解得 ,
则 ,
则 ,
故 的取值范围为 .