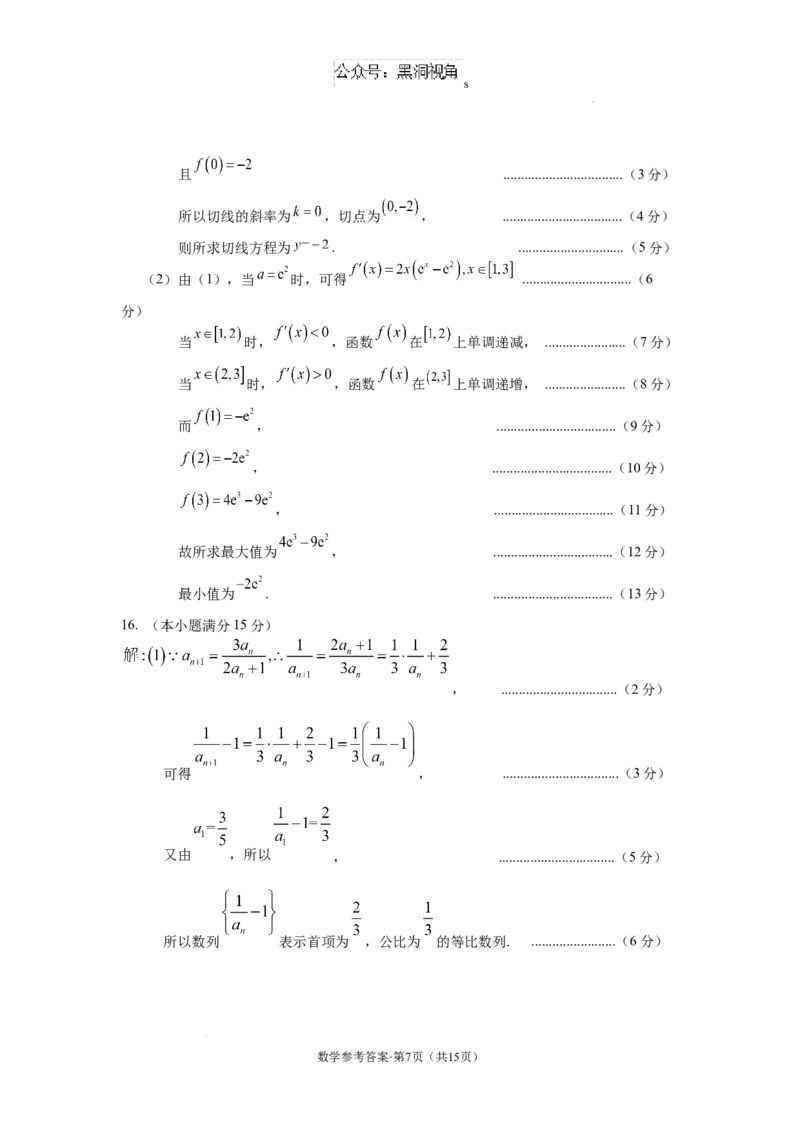文档内容
s
丽江市2025届高中毕业生复习统一检测
数学参考答案
一、单项选择题(本大题共8小题,每小题5分,共40分,在每小题给出的四个选项中,
只有一项符合题目要求)
题号 1 2 3 4 5 6 7 8
答案 B A D C D A B C
【解析】
1. 由 ,
得 ,
所以 .故选B.
2. ,故 ,解得 ,故 ,
又 ,故 .故选A
3. 由 两边平方得 , ,
由于 ,所以 ,
所以 .故选D
4. 若方程 表示椭圆,则 ,解得 且 ,
所以“ ”是“方程 表示椭圆”的必要不充分条件.故选C.
数学参考答案·第1页(共15页)
学科网(北京)股份有限公司s
5. 易知 ,
所以 ,
令 ,则 ,显然 ,
所以 为奇函数.故选D
6.
.故选A.
7. 不妨设五个点数为 ,由题意平均数为2,方差为0.4,
知 .
可知五次的点数中最大点数不可能为4,5,6.
五个点也不可能都是2,则五个点数情况可能是3,3,2,1,1,其方差为
,不合题意.
若五个点数情况为3,2,2,2,1,其方差为
,符合题意,其众数为2.故选B.
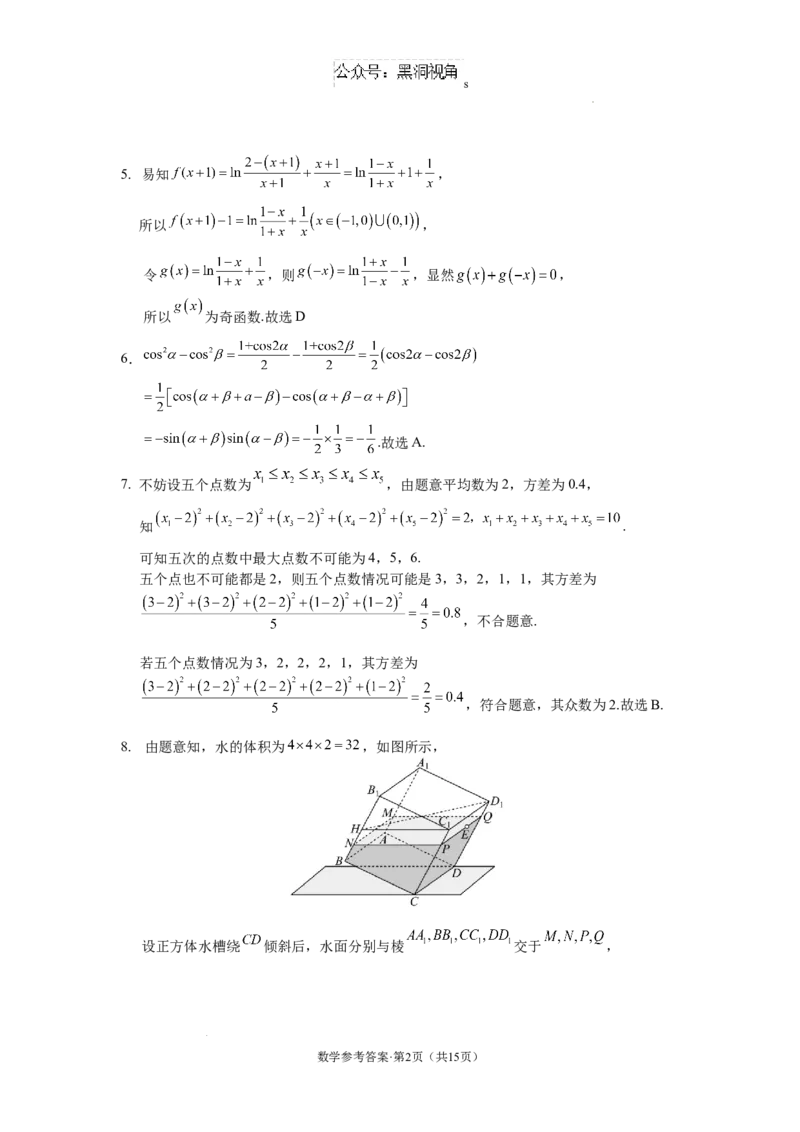
8. 由题意知,水的体积为 ,如图所示,
设正方体水槽绕 倾斜后,水面分别与棱 交于 ,
数学参考答案·第2页(共15页)
学科网(北京)股份有限公司s
由题意知 ,水的体积为 ,
所以 ,即 ,解得 ,
在平面 内,过点 作 交于 ,
则四边形 是平行四边形,且 ,
又侧面 与桌面所成的角即侧面 与水面 所成的角,
即侧面 与平面 所成的角,其平面角为 ,
在直角三角形 中, .故选C.
二、多项选择题(本大题共3小题,每小题6分,共18分,在每小题给出的四个选项中,
有多项符合题目要求,全部选对得6分,部分选对的得部分分,有选错的得0分)
题号 9 10 11
答案 ABD AC BCD
【解析】
9. 对于A.从小到大排序得:16,17,19,20,22,24,26,由 ,所以
下四分位数是17正确;
对于B, 正确;
对于C,由二项分布可得: ,错误;
对于D,由正态分布的对称性可得: ,正确.故选ABD.
10.因为 ,
所以 的最小正周期为 ,故A正确;
又由 ,故B错误;
数学参考答案·第3页(共15页)
学科网(北京)股份有限公司s
当 时,可得 ,
当 ,即 时, 取得最小值 ,
因为 , 恒成立,所以 ,
即实数 的取值范围为 ,故C正确;
由题意得函数 ,因为 ,
所以 ,又因为函数 有且仅有5个零点,
则满足 ,解得 ,
所以实数 的取值范围是 ,故D错误.故选AC.
11.A选项:由椭圆方程 ,所以 , ,所以 ,
所以 的面积为 ,故A错误;
B选项:当 或 时 为直角三角形,这样的点 有4个,
设椭圆的上下顶点分别为 , ,则 ,同理
,
知 ,所以当 位于椭圆的上、下顶点时 也为直角三角形,
其他位置不满足,满足条件的点 有6个,故B正确;
C选项:由于 ,
所以当 最小即 时, 取得最大值 ,故C正
数学参考答案·第4页(共15页)
学科网(北京)股份有限公司s
确;
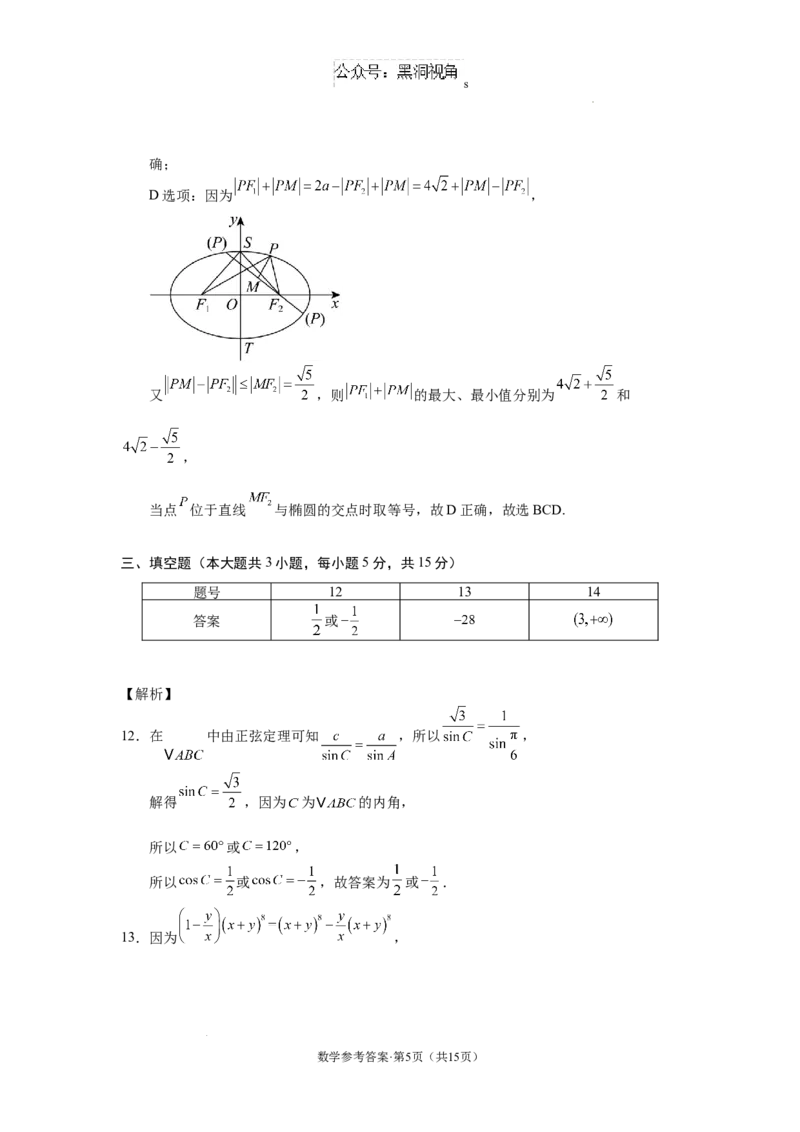
D选项:因为 ,
又 ,则 的最大、最小值分别为 和
,
当点 位于直线 与椭圆的交点时取等号,故D正确,故选BCD.
三、填空题(本大题共3小题,每小题5分,共15分)
题号 12 13 14
答案 或
【解析】
12.在 中由正弦定理可知 ,所以 ,
解得 ,因为 为 的内角,
所以 或 ,
所以 或 ,故答案为 或 .
13.因为 ,
数学参考答案·第5页(共15页)
学科网(北京)股份有限公司s
所以 的展开式中含 的项为 ,
故 的展开式中 的系数为 .故答案为 .
14.原不等式等价于 ,
也就是 ,
因为 均为 上的增函数,故 为 上的增函数,
故原不等式即为 ,故 对任意 恒成立,
故 对任意 恒成立,
设 ,则 ,
设 ,则 ,
故 在(0,+∞)上为减函数,而 ,
故当x∈(0,1)时, 即 ,故 在(0,1)上为增函数;
当x∈(1,+∞)时, 即 ,故 在(1,+∞)上为减函数,
故 ,故 .
四、解答题(本大题共5小题,共77分,解答应写出文字说明,证明过程或演算步骤)
15.(本小题满分13分)
解:(1)由函数 ,可得 .....(1分)
可得 ..................................(2分)
数学参考答案·第6页(共15页)
学科网(北京)股份有限公司s
且 ..................................(3分)
所以切线的斜率为 ,切点为 , ..................................(4分)
则所求切线方程为 . ..............................(5分)
(2)由(1),当 时,可得 ...............................(6
分)
当 时, ,函数 在 上单调递减, .......................(7分)
当 时, ,函数 在 上单调递增, .......................(8分)
而 , ..................................(9分)
, ..................................(10分)
, ..................................(11分)
故所求最大值为 , ..................................(12分)
最小值为 . ..................................(13分)
16. (本小题满分15分)
, .................................(2分)
可得 , .................................(3分)
又由 ,所以 , .................................(5分)
所以数列 表示首项为 ,公比为 的等比数列. ........................(6分)
数学参考答案·第7页(共15页)
学科网(北京)股份有限公司s
(2)由(1)可得 ,所以 ........(8分)
...............................................(11分)
,因为函数 为单调递增函数,....(12
分)
............................(15分)
17. (本小题满分15分)
解:(1)设AC与BD相交于点O,连接FO, ..................................(1
分)
∵四边形ABCD为菱形, , ..................................(2
分)
且O为AC中点, , , ..................................(3分)
又 , 平面BDEF,
∴ 平面BDEF, ..................................(5分)
又 平面 ,所以平面 平面 . ............................(6
分)
(2)
数学参考答案·第8页(共15页)
学科网(北京)股份有限公司s
连接DF,∵四边形BDEF为菱形,且 ,
为等边三角形,
∵O为BD中点,∴ ,又 , , 平面
ABCD,
平面ABCD.故OA,OB,OF两两垂直, .................................(7
分)
∴建立空间直角坐标系 ,如图所示, ..................................(8
分)
设 ,∵四边形ABCD为菱形, , .
为等边三角形,∴ .
,
∴ , , ............................(10
分)
设平面ABF的法向量为⃗n=(x,y,z),则
令 ,解得 , ...........................(12
分)
设AD与平面ABF所成角为 ,则AD与平面ABF所成角的正弦值为:
. .......................(15分)
18.(本小题满分17分)
解:(1)由题意可知,X= 4 , 6 , 8. ..................................(1分)
当两场比赛后结束,也即第一局的其中1人连续获得两场胜利,有两种情况,此
时 , , ........................(2
数学参考答案·第9页(共15页)
学科网(北京)股份有限公司s
分)
当三场比赛后结束,即第一局比赛的2人均未获胜,轮空者获胜,共有两种情况,
此时 , ; ................................(3分)
当四场比赛后结束,前三局比赛,甲乙丙三人各赢1场,进行第四场比赛,共有
2种情况,
此时 , ; ................................(4分)
所以三人总积分 的分布列为:
4 6 8
0.5 0.25 0.25
所以 . .................(6分)
(2)设事件 为“第一局乙对丙最终乙获胜”, 为“第一局乙对甲最终乙获胜”,
为“第一局甲对丙而最终乙获胜”,则有:
已知甲与乙比赛时,甲获胜的概率为 ,甲与丙比赛时,甲获胜的概率为 ,乙
与丙比赛时,乙获胜的概率为 .
其中 包含三种情况:
第一,第一局乙获胜,第二局乙获胜;
第二,第一局乙获胜,第二局甲获胜,第三局丙获胜,第四局乙获胜;
第三,第一局丙获胜,第二局甲获胜,第三局乙获胜,第四局乙获胜,
故 ; .......................(8分)
同理可得
;............(10
分)
; ...............(11
分)
显然 ,
数学参考答案·第10页(共15页)
学科网(北京)股份有限公司s
故 , ..............(13
分)
, ........................(15
分)
由于 ,
故 ,
所以 ;
故乙的最优指定策略是让乙和丙打第一局. .............................(17分)
19.(本小题共17分)
解:(1)由题意可得, ,解得 , ..................................(2分)
所以双曲线 的方程为 . ..........................(3分)
(2)当直线 斜率存在时,设直线 的方程为 ,
代入 可得 ,......(5
分)
当 时,即 时,直线 与双曲线的渐近线平行,只有一个公共点,
数学参考答案·第11页(共15页)
学科网(北京)股份有限公司s
即直线 的方程 为 , ......(6分)
当 时, ,
即 ,可得 ,此时直线 与双曲线相切,
直线 的方程为 ; ...................................(8分)
显然,当直线 斜率不存在时,直线 与双曲线有两个公共点,不满足;
综上所述,与双曲线 仅有1个公共点的直线有3条:
, , . ...............(9分)
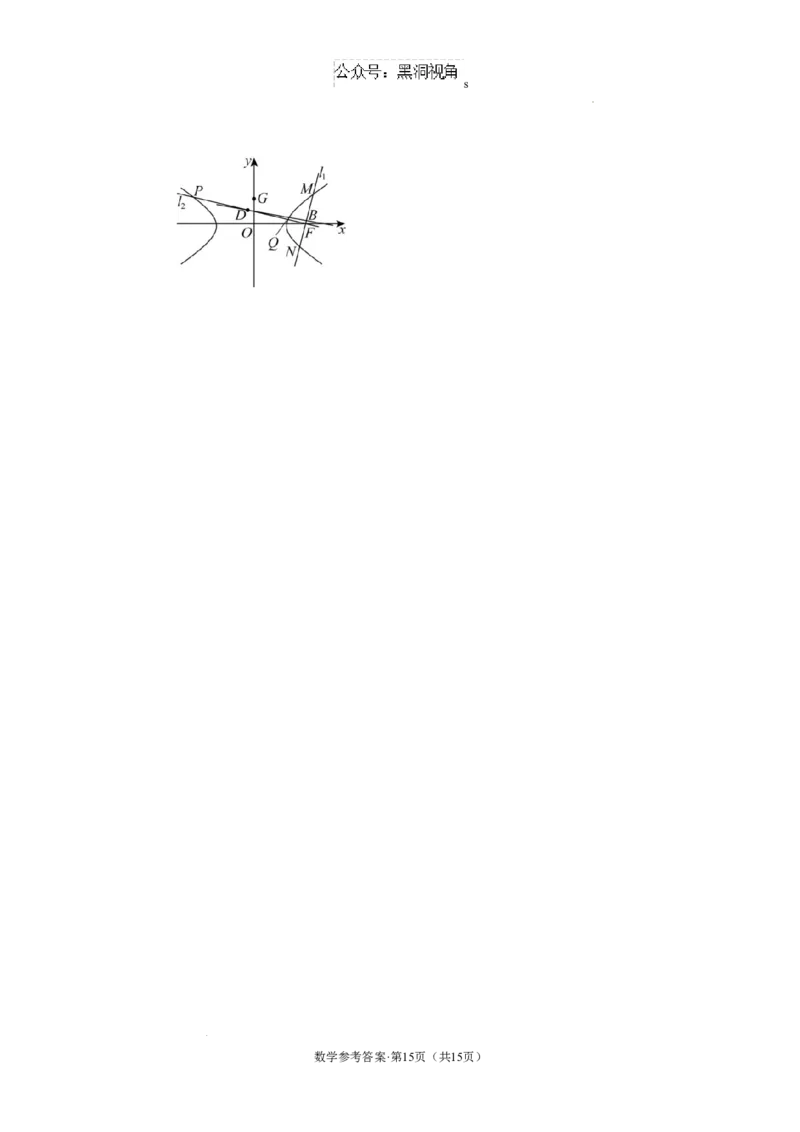
(3)当直线 的斜率不存在时,则 与 重合,又 ,即 ,
所以 , ,此时直线 的方程为 ,
则 到 的距离为 ; .................................(10分)
当直线 的斜率为0时,则 与 重合, , ,
此时直线 的方程为 ,则 到 的距离为 ; ................(11分)
当直线 的斜率存在且不为0时,设 的方程为 ,
设 ,
直线 的方程为 ,
联立 可得 ,
数学参考答案·第12页(共15页)
学科网(北京)股份有限公司s
,
由韦达定理可得 ,则 , ..........................(12
分)
所以 ,
所以 , ..........................(13
分)
联立 可得 ,
,
由韦达定理可得 ,则 , .......................(14
分)
所以 ,所以 ,
则
数学参考答案·第13页(共15页)
学科网(北京)股份有限公司s
, ,
所以直线 的方程为 , ......................(15分)
即 ,
所以 ,即 ,
故直线 过定点 , ..................(16分)
当 时,直线 与双曲线的渐近线平行,故与双曲线只有一个交点,舍去;
当 时,直线 与双曲线的渐近线平行,故与双曲线只有一个交点,舍去;
当 时, 的横坐标均为 ,此时,直线 的方程为 ,
过点 ;
综上所述,直线 过定点 .
所以点 到直线 的距离的最大值为 , .......(17
分)
数学参考答案·第14页(共15页)
学科网(北京)股份有限公司s
数学参考答案·第15页(共15页)
学科网(北京)股份有限公司