文档内容
天津市部分区 2024~2025 学年度第二学期期中练习
高二数学
第Ⅰ卷(共36分)
一、选择题(本题共9小题,每小题4分,共36分,在每小题给出的四个选项中,只有一项
是符合题目要求的.)
1. ( )
A.9 B.10C.11D.12
2.函数 的导数是( )
A. B. C. D.
3.一个做直线运动的质点的位移 与时间 的关系式为 ,若该质点的瞬时速度为
时,则 ( )
A.10B.5 C.1 D.0
4.在高二某班级中,有4名同学要参加足球、篮球、乒乓球三项比赛的报名活动,每人仅限选择一项参加,
其中甲同学无法参与足球比赛的报名,则不同的报名种数有( )
A.12B.16C.54D.81
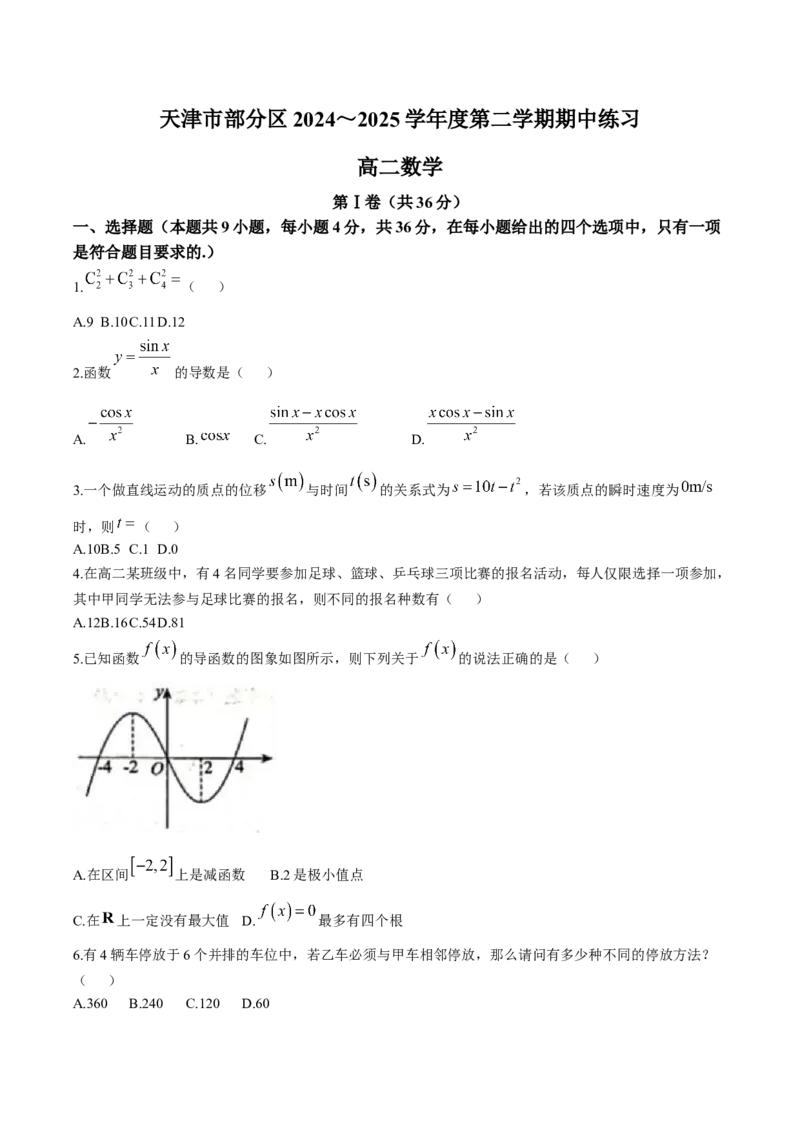
5.已知函数 的导函数的图象如图所示,则下列关于 的说法正确的是( )
A.在区间 上是减函数 B.2是极小值点
C.在 上一定没有最大值 D. 最多有四个根
6.有4辆车停放于6个并排的车位中,若乙车必须与甲车相邻停放,那么请问有多少种不同的停放方法?
( )
A.360 B.240 C.120 D.607.函数 的极值点的个数为( )
A.0 B.1 C.2 D.3
8.在 的展开式中,含 的项的系数是( )
A.120 B.15C. D.
9.设函数 ( ),有下列命题:
①当 时, 有三个零点;
②当 时, 是 的极小值点;
③存在实数 , ,使得 在区间 上存在最大值1.
其中是真命题的个数是( )
A.0 B.1 C.2 D.3
第Ⅱ卷(共84分)
二、填空题(本题共6小题,每小题4分,共24分.)
10.函数 的导数为______.
11.在 的展开式中,常数项为______.(请用数字作答)
12.第九届亚洲冬季运动会于2025年2月在哈尔滨成功举行.4名大学生分别前往冰球、速滑以及体育中心
三个场馆担任志愿者,每位大学生仅负责一个场馆,且每个场馆至少有一名志愿者,则所有不同的安排方
式共有______种.(请用数字回答)
13.在不超过20的质数中,随机挑选三个不同的数,则它们的乘积为偶数的组合方式共有______种.(请用
数字作答)
14.已知函数 ( ), ,若对任意 ,存在 ,使
成立,则 的取值范围是______.
15.已知函数 ,当 时, 的最小值为 ,则实数 的值为______.
三、解答题(本大题共5小题,共60分.解答应写出文字说明,证明过程或演算步骤.)16.(本小题满分12分)
已知函数 ( , , ),当 时, 取得极大值 ,当 时,
取得极小值.
(Ⅰ)求 , 的值:
(Ⅱ)求 的极小值.
17.(本小题满分12分)
袋子中有10个大小相同的小球,其中4个红球,6个白球.取一个红球得2分,取一个白球得1分,现在从
袋子中随机取出5个球,要求必须同时取出红球和白球.
(Ⅰ)请问有多少种取法能够使得总分数不超过7分?(请用数字作答)
(Ⅱ)当总分数恰好为7分时,先取出球,然后将这些球随机排列成一行,求红球互不相邻的不同排列方
式有多少种?(请用数字作答)
18.(本小题满分12分)
已知 的展开式的二项式系数和为128.
(Ⅰ)求 的值:
(Ⅱ)若展开式的第4项的系数为 ,求实数 的值.
19.(本小题满分12分)
设 是函数 的导函数, 是函数 的导函数,若方程 有实数解 ,则称点
为曲线 的“拐点”.经过探究发现:任何一个三次函数的图象都有“拐点”,且“拐
点”就是三次函数图象的对称中心.已知函数 的图象的对称中心为
(Ⅰ)求实数 , 的值;
(Ⅱ)求 的零点个数.
20.(本小题满分12分)
已知函数 ,其中 .
(Ⅰ)当 时,求曲线 在点 处的切线方程;(Ⅱ)若 的最大值是 ,求 的值;
(Ⅲ)设函数 ,若 有两个极值点 , ,证明:
.高二数学参考答案
一、选择题:本大题共9小题,每小题4分,共36分。
题 1 2 3 4 5 6 7 8 9
号
答 B D B C D C A C C
案
二、填空题(本题共6小题,每小题4分,共24分)
10. 11. 80 12. 36 13. 21 14. 15.
三、解答题:本大题共5小题,共60分.解答应写出文字说明,证明过程或演算步骤.
16.(本小题满分12分)
解:(Ⅰ)∵ ,∴ .
∵当 时, 取得极大值 ,当 时, 取得极小值
∴ 和 是方程 的两根,
有 ∴
(Ⅱ)由(Ⅰ)知,
∵当 时 取得极大值 ,
∴ ,∴
此时函数 的极小值为 .
17.(本小题满分12分)解:(Ⅰ)设取出 个红球 个白球,依题意可得 ,
因为 , ,所以 或 ,
∴符合题意的取法种数有 种.(有此表达式即可)
(Ⅱ)总分为7分,则取的个数为红球2个,白球3个,
将取出的球排成一排分两步完成,
第一步先取球,共有 种,
第二步再排,先把3个白球全排列,再将2个红球插空,
共有 ,
根据分步乘法计数原理可得不同排法有 种.
18.(本小题满分12分)
解:(Ⅰ)因为 展开式的二项式系数和为 ,
所以 ;
(Ⅱ)因为 的展开式的第4项为 ,
所以 ,解得 .
19.(本小题满分12分)
解:(Ⅰ)因为 ,
所以 ,所以 ,
又因为 的图象的对称中心为 ,
所以 ,解得(Ⅱ)由(Ⅰ)知, ,
∴ ,
令 ,得 或 ,
所以当 时, , 单调递增;
当 时, , 单调递减;
当 时, , 单调递增.
因为 , ,
又当 时, ;当 时, ,
所以 有3个零点.
20.(本小题满分12分)
解:(Ⅰ)当 时,则 , .
可得 , ,
即切点坐标为 ,切线斜率 ,
所以切线方程为 ,即 .
(Ⅱ) 的定义域为 ,而 .
当 时, , 单调递增,
当 时, , 单调递减,
所以 的最大值为 .故 ,整理得到 ,其中 ,
设 , ,则 ,
故 为 上的减函数,而 ,
故 的唯一解为 ,故 的解为 .
综上所述, .
(Ⅲ)由题意得,函数 的定义域为 ,且 ,
,令 ,
因为函数 有两个极值点 , ,则 , 是方程 的两个根,
得 ,即 ,且 , ,
,
令 , ,则 ,
当 时, ,则 在区间 上单调递减,
从而 ,故 .