安徽省合肥市第四中学2023-2024学年高三上学期11月月考数学答案(1)_2023年11月_0211月合集_2024届安徽省徽师联盟高三11月质量检测卷_安徽省徽师联盟2024届高三11月质量检测卷数学

2024高三11月质量检测卷·数学 参考答案及解析 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 D C D C A C B C AB BC ABC AC 1.D .  x1    【解析】因为M x| 0=3 x1，N  yR|y  x 1 [1,) ，所以  x3  (C M)N [1,) U 2.C . 【解析】因为A中， p不是q的充分条件，则q不是 p的必要条件；B中，若一个三角形三 边分别为5,6,9，另一三角形三边分别为6,6,8,,两个三角形周长相等，却不全等，则q不是 p的必要条件；D中，若x 2,x2 2，x2不是无理数，p不是q的充分条件，则q不 是 p的必要条件 3.D . 3 1 3 6 9 【解析】应为扇形的弧长l 2 ，S     sin1 2 sin1 sin1 sin21 4.C . 【解析】因为 f(x1)为奇函数，则关于原点对称，所以 f(x)关于点(1,0)对称；因为 f(x) 在(1,)上单调递减，则 f(x)在R上单调递减；故， f(1) f(3)， f(3) f(3)， f(1) f(3). 5.A .   2  2 【解析】由题意得，t sin(2  ) ，得P( , )，又因为P向左平移s个单位 4 4 2 4 2  2 2  长度得到点P( s, )，代入得， cos( 2s)sin2s ， 4 2 2 2  3  s  k或s  k，因为s 0，所以s的最小值为 8 8 8 6.C . 1 1 【解析】在BDC和ADC中，由余弦定理可得a2  c2 22 c 2cosBDC ， 4 2 1 1 1 b2  c2 22 c 2cos(BDC) ；联立可得，a2 b2  c2 4 7，则 4 2 2 1 6 3 c 6，S   2 sinBDC  ；得sinBDC 1,0BDC , BDC 2 2 2  14 BDC  ,b AD2CD2  2 2 7.B . 【解析】 已知3f(x)cosx f (x)sinx 0 ，令g(x) f(x)sin3x,则 g(x)3f(x)sin2xcosx f(x)sin3x sin2x[3f(x)cosx f(x)sinx]0 ，所以   g(x)在R上单调递减，又因为 f(x)偶函数，所以 f( ) f( )2， 6 6 【数学试题答案 第1页 共7页】 {#{QQABCYYQogAIABAAAQgCUwXCCgGQkBECCKoOhFAMIAABQQFABAA=}#} 1  1     f( )( )3f( ) ，g(x ) f(x )sin3(x ) f(x )cos3x ，所 6 2 6 4 2 2 2 2  1     2 以 f(x )cos3x 0等价于g(x ) g( ) ，则x  ,解得x ， 2 4 2 6 2 6 3 2 所以不等式的解集为( ,) 3 8.C . 【解析】由y  f (32x)为奇函数可得 f(32x)f(32x)，即 f(3x)f(3x)，  f(3x) f(3x)， f(3x) f(3x)0 ，即g(3x)g(3x)0，所以函数 1 y  g(x)的图像关于直线x3对称。由 y  x f (x2)是偶函数可得 3 1 1 1 y  f(x2)为奇函数，  f(x2)  f(x2)0, 即 3 3 3 2 1 g(x2)g(x2) ，所以函数 y  g(x)的图像关于点(2, )对称；将x1代入 3 3 1 2 g(3x)g(3x)0，得g(4) ，将x2代入g(x2)g(x2) 得 3 3 2 1 g(4)g(0) 得g(0) ，将x3代入g(3x)g(3x)0，得g(0)g(6)0， 3 3 1 故g(6) 3 9.AB 【解析】A{x|x22x30,xR},A{1,3},AB  A,B A 2(a1) a2 ①当B  A,即B {1,3}时，得 2, 3; 无解 a a 1 ②当B ,即4(a1)24a(a2)16a40a 4 ③当B {1},即16a40,a2a2a20; 无解 1 ④当B {3},即16a40,9a6a6a20a  4 1 故，a的取值范围为(, ] 4 10.BC; 【解析】A选项中，只有a240,即a2或a 2时, x2 ax10有实数解 1 1 1 a a B选项中，若   ,则a23abb2  0, 因为b0，所以( )2 3 10 a b ba b b a 3 5 1 1 1 解得  ，令a 3 5,b2，则有ab0且   ； b 2 a b ba C选项中，正方形属于四边形；D选项中，三角形两边之差要小于第三边，故错误； 11.ABC 【解析】 x 3,5 x x  x  x  x 3, x 8 1 1 2 2 1 2 2 1 1 x x  ,x x  x x  24,a 又 x x 5,(x x )24x x  25， 1 2 a 1 2 1 2 24 1 2 1 2 1 2 【数学试题答案 第2页 共7页】 {#{QQABCYYQogAIABAAAQgCUwXCCgGQkBECCKoOhFAMIAABQQFABAA=}#}121 35 11 (b1)2 25a24a ,b 或b 576 24 24 1 x x  0,x ,x 同号. x 3,3 x 3 1 2 a 1 2 1 1 若3 x 0,则3 x  x 0,则x x 3,与x x 5矛盾 1 1 2 1 2 1 2 b1 11 0 x 3,则x 5,x  x 0,x  x  0,b1 .所以b 1 2 1 2 1 2 a 24 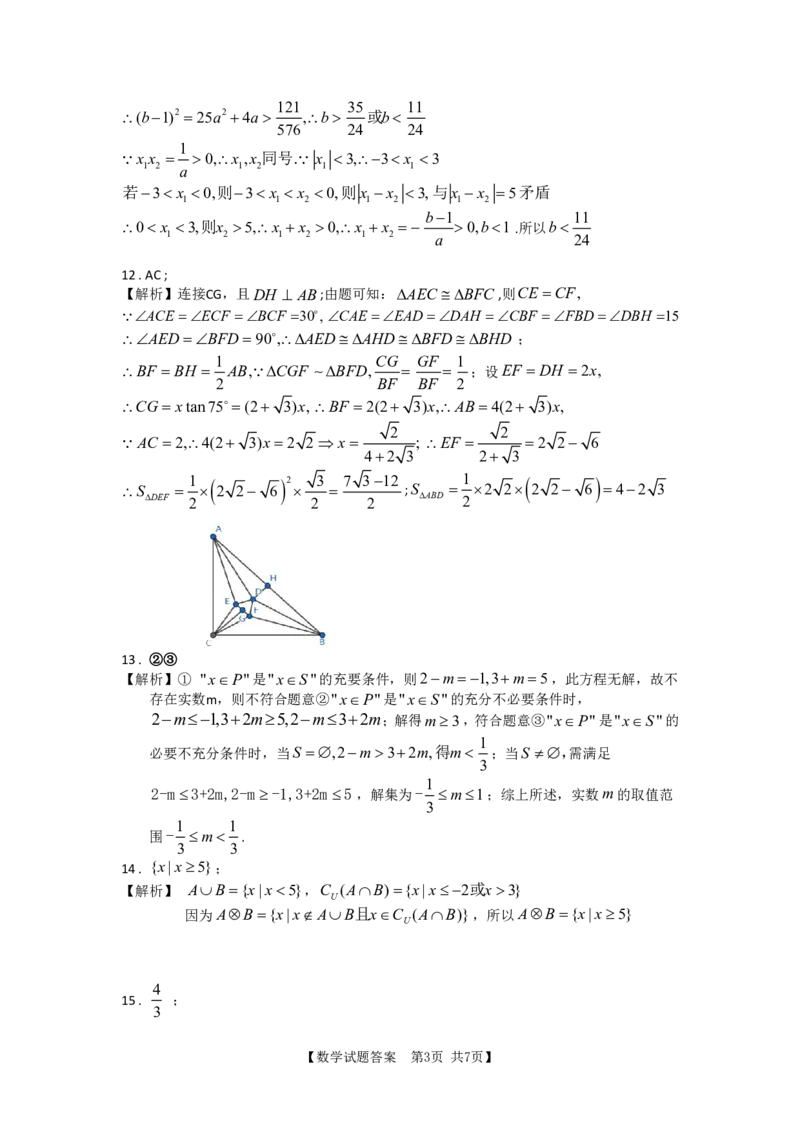12.AC; 【解析】连接CG，且DH  AB;由题可知：AEC BFC,则CE CF, ACE ECF BCF 30, CAE EADDAH CBF FBDDBH 15 AEDBFD 90,AEDAHDBFDBHD ； 1 CG GF 1 BF  BH  AB,CGF BFD,   ；设EF  DH  2x, 2 BF BF 2 CG  xtan75 (2 3)x,BF  2(2 3)x,AB 4(2 3)x, 2 2 AC 2,4(2 3)x 2 2  x  ; EF   2 2 6 42 3 2 3 1  2 3 7 3 12 1   S   2 2 6   ;S  2 2 2 2 6 42 3 DEF 2 2 2 ABD 2 13. ②③ 【解析】① "xP"是"xS"的充要条件，则2m1,3m5，此方程无解，故不 存在实数m，则不符合题意②"xP"是"xS"的充分不必要条件时， 2m1,32m5,2m32m；解得m3，符合题意③"xP"是"xS"的 1 必要不充分条件时，当S ,2m32m,得m ；当S ，需满足 3 1 2-m 3+2m,2-m -1,3+2m 5 ，解集为- m1；综上所述，实数m的取值范 3 1 1 围- m . 3 3 14. {x|x5}； 【解析】 AB {x|x5}，C (AB){x|x2或x 3} U 因为AB {x|xAB且xC (AB)}，所以AB {x|x5} U 4 15. ； 3 【数学试题答案 第3页 共7页】 {#{QQABCYYQogAIABAAAQgCUwXCCgGQkBECCKoOhFAMIAABQQFABAA=}#} 【解析】因为函数 f(x)sin(x) (0,0 ) 是R上的奇函数，则 2 f(x)f(x)，即sincosxcosxsin，又因为0，所以sin0，  3 因为0 ，所以0；故 f(x)sinx；又因为图象关于点A( ,0)对称， 2 4 3 则 k,kN ； 4 4k  1 2   ,kN ，因为函数在区间[0, ]上是单调函数，则   04； 3 4 2  4 4 所以 3 16.①③; 【解析】①:因为函数 y  x31的值域是全体实数集，所以对于任意xR,存在 yR,使 f(x) f(y) 2成立，符合题意 2 ②: y ex(x1) yex(x2),当x2时, y0,该函数此时单调递增， 当x2时， y0该函数此时单调递减，所以当x2时，函数有最小值e2 f(x) f(y) 若 y ex(x1)是“半差值”为2的函数，因此有xR,存在 yR,使 2成 2 立，即 f(x) f(y)4,对于xR, f(x)e2,而 f(y)4e24,显然 f(x) f(y) xR,不一定存在 yR,使 2成立，故本函数不符合题意； 2 ③:因为函数 y log x的的值域是全体实数集，所以对于任意xR,存在 yR,使 2 f(x) f(y) 2成立，符合题意； 2 ④:若y sinx是实数集上的“半差值”为2的函数，因此有xR,存在 yR,使 f(x) f(y) 2,即 f(x) f(y)4，对于xR, 1 f(x)1,而3 f(y)45, 2 显然 f(x) f(y)4恒不成立，故假设不成立，所以本函数不符合题意， 17. 【解析】（1）解不等式x2 x20，解得2 x1； 当m1时，解不等式x2 3m20，得2 x1 因为A,B同时成立时，x的取值范围为(2,1) ..........4分 （2）P:xA,x2(12a)xa2a 8 P:xA,x2(12a)xa2a8为真命题 设 f(x) x2 (12a)xa2 a8，则 f(x)0在(2,1)上有解 f(2)a25a606a1； f(1)a2 a602a3 综上所述，a取值范围为 6,3  ...........6分 18. 【解析】（1） sinB a2 b2 c2 2bccosA bcosA sinBcosA     sinC 0, 2sinCsinB b2a2c2 2accosB acosB sin AcosB 【数学试题答案 第4页 共7页】 {#{QQABCYYQogAIABAAAQgCUwXCCgGQkBECCKoOhFAMIAABQQFABAA=}#}2sinCcosAsinBcosAsin AcosBsin(B A)sinC ， 1  sinC 0,cosA .0 A,A ...........6分 2 3 3 1 1 (2)T sin2 Asin2Bsin2C   (1cos2B) (1cos2C) 4 2 2 7 1 7 1 1 3    (cos2Bcos2C)   cos2B sin2B 4 2 4 2 2 2  7 1    cos(2B ) 4 2 3 2 4   5 0 B ,02B , 2B  3 3 3 3 3  1 3 9 1cos(2B ) , T  3 2 2 4 ..............6分 x2 b x2 b 19. 【解析】（1）由 f(x) blnx得 f(x) x  ； 2 x x b0 f (x)0得x b f(x)的单调递增区间为[ b,)，单调递减区间为(0, b)； b(1lnb) f(x)在x b 处的极小值为 f( b) ，无极大值 ...........4分 2 （2）当b0, f(x)0恒成立， f(x)在(0,)上单调递增，故 f(x)在区间(1,e2]内至 多只有一个零点； b(1lnb) 当b0时，由（1）得 f(x)在(0,)上最小值为 f( b) ，若 f(x)在 2 1 b e2 f( b)0 e4 区间(1,e2]内恰有两个零点，则需满足 ，整理得eb ........8分 f(1)0 4 f(e2)0 20. 【解析】（1）由图象可得， f(x)的最小正周期   2 T 4(  ),  2, 0, 2 3 12 T    由2  2k,kZ 解得 2k,kZ ， 3 2 6     , ； f(x)2sin(2x ) 2 6 6   3  5 由2k 2x 2k 解得k  xk 2 6 2 3 6   5 所以函数 f(x)的单调递减区间为  k ,k  .........4分  3 6  （2）令t  f (x)，方程可化为t2 (4a)t3a 0，解得t 1,t a3 1 2 【数学试题答案 第5页 共7页】 {#{QQABCYYQogAIABAAAQgCUwXCCgGQkBECCKoOhFAMIAABQQFABAA=}#} 1  7  令 f(x)1,可得sin(2x ) ；x   ,  ，可得 6 2  12 4 5    5      2x  ；2x  或2x  ；故x 或x0 4 6 3 6 6 6 6 3 因为方程 f 2(x)(4a)f(x)3a 0 存在4个不相等的实数根，a31，  7   且方程 f(x)a3在  , 上有两个根，所以函数 f(x)2sin(2x )    12 4 6  7   7  x   ,  的图象与函数 y a3的图象有两个交点；x   ,  时，  12 4  12 4 4        2x  ；由正弦函数性质可得，当  2x  时 f(x)为增函数， 3 6 3 2 6 3 3 4   2 2 f(x) ；当  2x  时，f(x)为减函数，2 f(x) ， 2 3 6 2 2 所以t a3取值范围应在2,1 或(1, 3]；即2a31或 2 1a3 3；解得1a2或2a3 3 ...........8分 2x 2x 1 2x 2x 1 21. 【解析】（1） f(x) ， f(x)t2x  , t2x  ，即 2 2 2 2 1 3 1 1 t  (22x 2x 1) 在x(0,)有解，令m2x(0,1)，所以t   (m )2；当 2 8 2 2 1 3 1 3 1 m 时，t  ；又当m1时，t  ；即t[ , ) .........4分 2 min 8 2 8 2 （2）f(2x)2bg(x)0，即 22x 22x b(2x 2x)0，令2x 2x  m,因为x 1,2  ， 2 3 15 所以 y 2x 2x为增函数，所以m[ , ]，则22x 22x  m2 2，所以 2 4 m2 2 m2 2 3 15 m2 2 bm0，化为b 对任意的m[ , ]恒成立，(m) 在 2 2m 2 4 2m 3 15 m2 2 m 1 3 15 m[ , ]的最大值，(m) (  )在m[ , ]上单调递减，所以当 2 4 2m 2 m 2 4 3 3 3 2 17 17 m 时，取得最大值，( )(  ) ，所以b ，实数b的取值范围为 2 2 4 3 12 12 17 [ ,) ..........8分 12 22. 【解析】（1）因为 f(x)2lnxax23，函数 f(x)的定义域为(0,)，所以 2 22ax2 f(x) 2ax  ， x x 当a0时， f(x)0在x(0,)上恒成立，故 f(x)在(0,)上单调递增； a a 当a 0时，若x(0, ),则 f(x)0，故 f(x)在(0, )上单调递增； a a a a 若x( ,)，则 f(x)0，故 f(x)在( ,)上单调递减； a a 【数学试题答案 第6页 共7页】 {#{QQABCYYQogAIABAAAQgCUwXCCgGQkBECCKoOhFAMIAABQQFABAA=}#}a 综上所述，当a0时， f(x)在(0,)上单调递增；当a 0时， f(x)在(0, )上单调 a a 递增，在( ,)上单调递减； .........4分 a a a a （2）因为 f(x)的极大值为4，所以由（1）得a 0；所以 f( )2ln a( )234， a a a 1 解得a  ..........2分 e2 1 2(ex)(ex) （3）证明：由（2）得此时 f(x)2lnx x23，即 f(x) e2 e2x 当0 xe时， f(x)0，函数 f(x)在(0,e)上单调递增；当xe时， f(x)0， 函数 f(x)在(e,)上单调递减；所以函数 f(x)在xe时有极大值，极大值为4； x x x x 即若证明 f( 1 2)0，即证 1 2 e，即x x  2e； 1 2 2 2 令x  x ，则证明x 2ex e 1 2 2 1 令F(x) f(x) f(2ex),x(0,e)，则 1 x 1 2ex 4e 4 F(x)2(  )2(  )  0 ， x e2 2ex e2 x(2ex) e x x 所以F(x)在(0,e)上单调递增，所以F(x)F(e)0，所以 1 2 e 2 x x 故 f( 1 2)0。 ..........6分 2 【数学试题答案 第7页 共7页】 {#{QQABCYYQogAIABAAAQgCUwXCCgGQkBECCKoOhFAMIAABQQFABAA=}#}