文档内容
龙岩市 2024 年高中毕业班三月教学质量检测
数学试题
(满分:150分 考试时间:120分钟)
注意事项:
1.考生将自己的姓名、准考证号及所有的答案均填写在答题卡上,
2.答题要求见答题卡上的“填涂样例”和“注意事项”.
一、选择题:本题共 8小题,每小题 5分,共 40分.在每小题给出的四个选项中,只有一项是符
合题目要求的.
1.已知集合A= { x∣x2 −x−2<0 } ,B= { x∣3x −1>0 } ,则A∩B =( )
A.
(−∞,0 )
B.
(
0,2
)
C.
(−1,0 )
D.
(−1,2 )
2.已知复数z满足i⋅z =3+4i,则z−z =( )
A.−6i B.6i C.-8 D.8
3.已知互相垂直的平面α,β交于直线l,若直线m,n满足m∥α,n⊥β,则( )
A. m∥l B. m∥n C.m⊥n D.n⊥l
4.已知向量a =(−4,3 ) ,b =( 1,−2 ),则cos a+2b,b =( )
π π π 2π
A. B. C. D.
4 3 2 3
2x
5. −1(x+ y)7的展开式中x5y2的系数为( )
y
A.-91 B.-21 C.14 D.49
π 1 4
6.已知0<β<α< ,cos(α+β)= ,sin(α−β)= ,则tanαtanβ的值为( )
2 5 5
1 3 5
A. B. C. D.2
2 5 3
kp
7.已知直线l:y=kx− 与抛物线C:y2 =2px(p>0)相交于A,B两点,以AB为直径的圆与抛物线C的准
2
线相切于点M (−1,−1 ) ,则 AB =( )
9
A.4 B. C.5 D.6
2
8.已知函数 f ( x ) 的定义域为R,且 f ( x+ y )+ f ( x− y )− f ( x ) f ( y )=0, f (−1 )=1,则( )
A. f
(
0
)=0
B. f
(
x
)
为奇函数
C. f
(
8
)=−1
D. f
(
x
)
的周期为3
学科网(北京)股份有限公司二、多选题:本题共 3小题,每小题 6分,共 18分.在每小题给出的选项中,有多项符合题目要
求.全部选对的得 6分,部分选对的得部分分,有选错的得 0分.
9.下列命题正确的是( )
A.若aab>b2
B.若a
a b
b
D.若02 ab
2
( )
10.已知点B 2,1 与圆C:(x−2)2 +(y−2)2 =4,A是圆C上的动点,则( )
A. OA 的最大值为2 2+2
B.过点B的直线被圆C 截得的最短弦长为 3
C.8−4 2 ≤OC⋅OA≤8+4 2
2 5
D.∀x∈R,CO−xOB 的最小值为
5
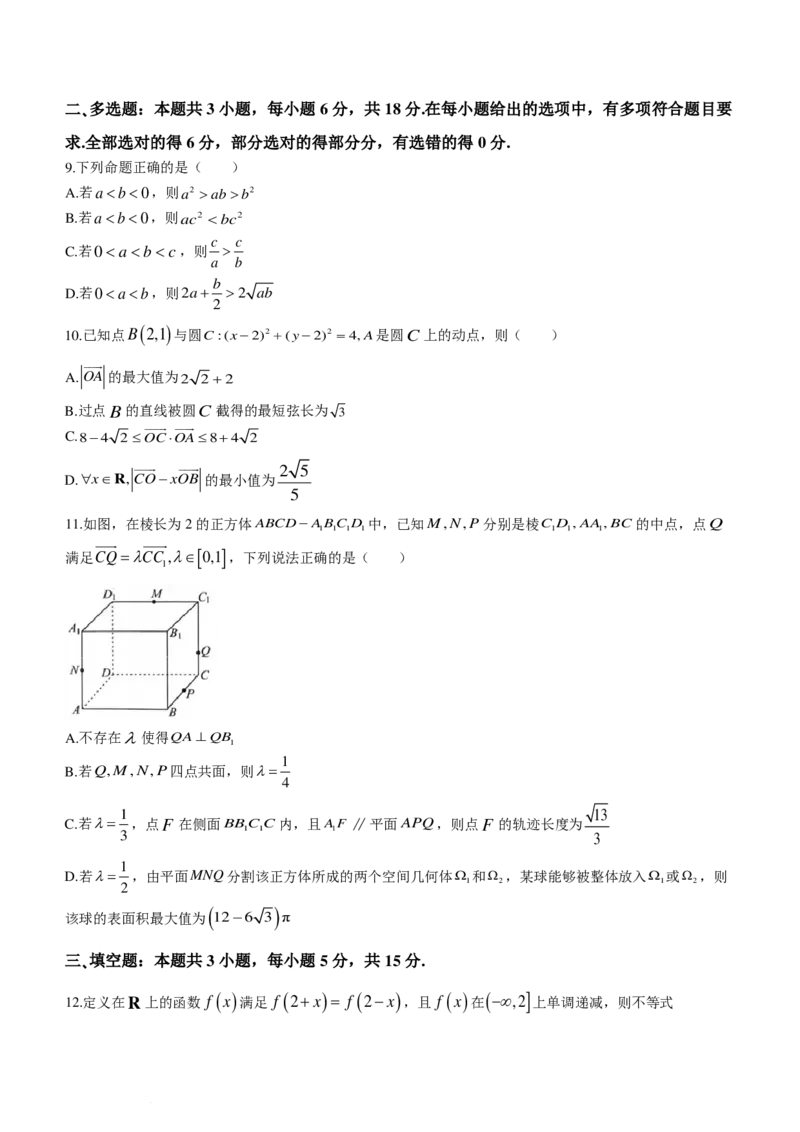
11.如图,在棱长为2的正方体ABCD−ABC D 中,已知M,N,P分别是棱C D ,AA,BC 的中点,点Q
1 1 1 1 1 1 1
满足CQ=λCC ,λ∈[ 0,1 ] ,下列说法正确的是( )
1
A.不存在λ使得QA⊥QB
1
1
B.若Q,M,N,P四点共面,则λ=
4
1 13
C.若λ= ,点F 在侧面BBCC内,且AF ∥平面APQ,则点F 的轨迹长度为
1 1 1
3 3
1
D.若λ= ,由平面MNQ分割该正方体所成的两个空间几何体Ω 和Ω ,某球能够被整体放入Ω 或Ω ,则
1 2 1 2
2
( )
该球的表面积最大值为 12−6 3 π
三、填空题:本题共 3小题,每小题 5分,共 15分.
12.定义在R上的函数 f ( x ) 满足 f ( 2+x )= f ( 2−x ) ,且 f ( x ) 在 (−∞,2 ] 上单调递减,则不等式
学科网(北京)股份有限公司f ( 2x+3 )≤ f ( 1 ) 的解集为__________.
13.在ABC中,∠BAC =120,AB=2,AC =3,D为BC上一点,AD为∠BAC的角平分线,则AD=
__________.
x2 y2
14.斜率为-1的直线与椭圆C: + =1(a>b>0)交于A,B两点,点T 是椭圆上的一点,且满足
a2 b2
TA⊥TB,点P,Q分别是OAT,OBT 的重心,点R是TAB的外心.记直线OP,OQ,OR的斜率分别为
1
k ,k ,k ,若kk k =− ,则椭圆C 的离心率为__________.
1 2 3 1 2 3 8
四、解答题:本题共 5小题,共 77分.解答应写出文字说明、证明过程或演算步骤.
15.(本题满分13分)
2023年秋季,支原体肺炎在我国各地流行,该疾病的主要感染群体为青少年和老年人.某市医院传染病科从该
市各医院某段时间就医且年龄在70岁以上的老年人中随机抽查了200人,并调查其患病情况,将调查结果整
理如下:
有慢性疾病 没有慢性疾病
未感染支原体肺炎 60 80
感染支原体肺炎 40 20
(1)试根据小概率值α=0.05的独立性检验,分析70岁以上老年人感染支原体肺炎与自身慢性疾病是否有
关?
(2)用样本估计总体,并用本次抽查中样本的频率代替概率,从本市各医院某段时间就医且年龄在70岁以
上的老年人中随机抽取3人,设抽取的3人中感染支原体肺炎的人数为X ,求X 的分布列和数学期望
( )
E X .
n(ad −bc)2
附:χ2 = ,n=a+b+c+d .
( a+b )( c+d )( a+c )( b+d )
α
0.10 0.05 0.025 0.010 0.001
x 2.706 3.841 5.024 6.635 10.828
α
16.(本题满分15分)
如图,在四棱锥P− ABCD中,PAB是边长为2的正三角形,BC = AB =2AD,AD∥
BC,AB ⊥ BC,设平面PAB∩平面PCD=l.
学科网(北京)股份有限公司(1)作出l(不要求写作法);
(2)线段PB上是否存在一点E,使l∥平面ADE?请说明理由;
(3)若BC ⊥l,求平面PAB与平面PCD的夹角的余弦值.
17.(本题满分15分)
( )
2 n2 +n
设等差数列 { a } 的公差为d(d >1),令b = ,记S ,T 分别为数列 { a } , { b } 的前n项和.
n n n n n n
a
n
{ }
(1)若4a =4a +a ,S +T =13,求数列 a 的通项公式;
2 1 3 2 2 n
b
(2)若数列 { c } 是公比为正数的等比数列,a =c =2,a =2c −1,c =2a +2,求数列 n的前n项
n 1 1 2 1 3 2 c
n
和A .
n
18.(本题满分17分)
已知函数 f ( x )=ln ( 2mx ) ,m是大于0的常数,记曲线 y = f ( x ) 在点 ( x , f ( x )) 处的切线为l,l在x轴上的
1 1
截距为x ,x >0.
2 2
(1)若函数g ( x )= x2 −1−af ( x ) ,a∈R,求g ( x ) 的单调区间;
1
(2)当x +x > 时,求x 的取值范围.
1 2 m 1
19.(本题满分17分)
已知双曲线C:x2 − y2 =4,A是双曲线C 的左顶点,直线l:x =my+t ( m≠ ±1 ) .
( )
(1)设直线l过定点B 1,0 ,且交双曲线C 于E,F两点,求证:直线 AE与AF 的斜率之积为定值;
(2)设直线l与双曲线C 有唯一的公共点M .
(i)已知直线l与双曲线C 的两条渐近线相交于两点R,S,求证:MR=MS ;
(ii)过点M 且与l垂直的直线分别交x轴、 y 轴于P ( x,0 ) ,Q ( 0,y ) 两点,当点M 运动时,求点N ( x,y ) 的
轨迹方程.
学科网(北京)股份有限公司