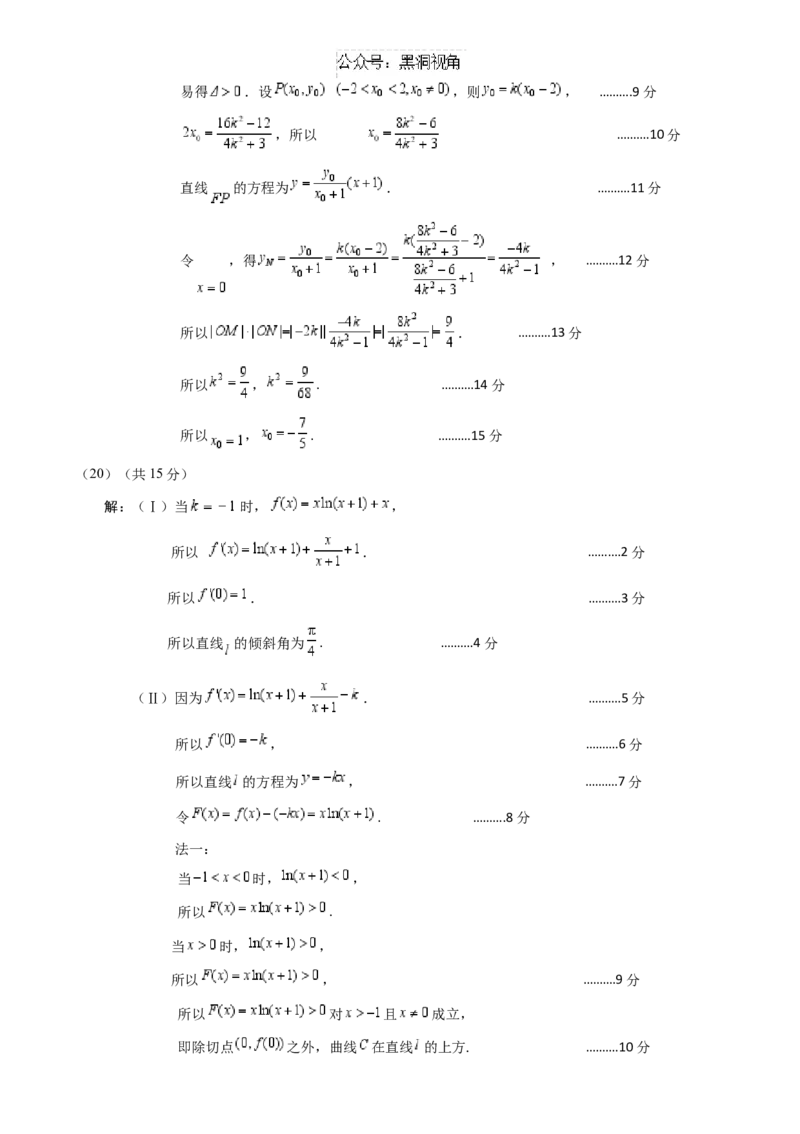文档内容
2024 年定位考试
数学参考答案
一、选择题(共10小题,每小题4分,共40分)
(1)C (2)D (3)B (4)A (5)D
(6)B (7)D (8)C (9)C (10)A
二、填空题(共5小题,每小题5分,共25分)
(11) (12)
(13) (14) (答案不唯一)
(15)① ③ ④
说明:12, 13, 14题都是第一个空3分,第二个2分;
15题 对一个给1分,对两个给3分,全对给5分,如果有错的,则给0分。
三、解答题(共6小题,共85分)
(16)(共14分)
解:(Ⅰ)连接 ,在 中,
因为 分别为 , 的中点,
所以 ……….2分
又 平面 , 平面
所以 平面 . ……….4分
(Ⅱ)因为直三棱柱
所以 平面 ,
所以 ,
……….5分
又 为直角,
所以 , ……….6分
又
所以 平面 , ……….7分
所以 ,
由(Ⅰ) ,
所以 . ……….8分
(Ⅲ)建立空间直角坐标系 , ……….9分
则 , , , .因此 , .
设平面 的法向量为 ,则
即 ……….11分
令 ,于是 . ……….12分
设直线 与平面 所成角为 .
所以 . ……….14分
(17)(共13分)
解:(Ⅰ)由正弦定理 , ……….3分
所以 . ……….4分
代入得
所以 . ……….5分
(Ⅱ)选择条件①: . ……….6分
因为 , 所以 . ……….8分
因为 为锐角,所以 ……….9分
由余弦定理 , ……….11分
代入得到
所以 .
解得 , (舍). ……….12分
所以 的周长为 . ……….13分
选择条件②: . ……….6分
因为 ,所以 , ……….7分
所以 ,以下同选择①.
选择条件 ③: . ……….6分
因为 , 所以 . ……….8分因为 为锐角,所以 ……….9分
由余弦定理 , ……….11分
代入得到
所以 , ……….12分
所以 的周长为 . ……….13分
(18)(共13分)
解:(Ⅰ)设事件 为“某一天此款甜品销售量不超过 个”, ……….1分
所以 . ……….4分
(Ⅱ) . ……….5分
,
,
,
,
所以 的分布列为
……….9分所以
……….11分
(Ⅲ)可以认为此款甜品的销售情况发生了变化.
因为以前此款甜品的日销售量大于70个的频率为 ,
现在30天中有20天销售量大于70个,其频率 远大于改进前,
所以可以认为此款甜品的销售情况发生了变化. ……….13分
(也可认为无法确定有无变化,30天中有20天销售量大于70个是随机事件,按之前频率
估计计算30天中有20天销售量大于70个的概率比较小,一般不容易发生,但还是有可
能发生的,所以无法确定有没有变化)
(19)(共15分)解:(Ⅰ)由题设,
所以 的方程为 . ……….5分
(Ⅱ)法一:
设 ,所以 ……….6分
所以 , ……….7分
直线 的方程为 . ……….8分
令 ,得 ……….9分
又 , ……….10分
直线 的方程为 . ……….11分
令 ,得 , ……….12分
所以 .
所以 , ……….14分
所以 ,
所以 ,
所以 , . ……….15分
法二:
由题意直线 斜率存在,且不为0,设直线 的方程为 .
……….6分
令 ,得 ……….7分
由 得 . ……….8分易得 .设 ,则 , ……….9分
,所以 ……….10分
直线 的方程为 . ……….11分
令 ,得 , ……….12分
所以 . ……….13分
所以 , . ……….14分
所以 , . ……….15分
(20)(共15分)
解:(Ⅰ)当 时, ,
所以 . ……….2分
所以 . ……….3分
所以直线 的倾斜角为 . ……….4分
(Ⅱ)因为 . ……….5分
所以 , ……….6分
所以直线 的方程为 , ……….7分
令 . ……….8分
法一:
当 时, ,
所以 .
当 时, ,
所以 , ……….9分
所以 对 且 成立,
即除切点 之外,曲线 在直线 的上方. ……….10分法二:
因为 ,
所以 时, .
时, , ,
与 的变化情况如下表:
↘ ↗
……….9分
所以,函数 在 处取得最小值 ,
所以 对 且 成立,
即除切点 之外,曲线 在直线 的上方. ……….10分
(Ⅲ)因为函数 在 上单调递增,
所以 对 成立 ……….11分
令 , ……….12分
所以 , ……….13分
所以 对 成立, 所以 在 上单调递增, ……….14分
所以只需 , 所以 .
所以 的取值范围为 . ……….15分
(21)(共15分)
解:(Ⅰ) , , , , . ……….4分
(Ⅱ)假设数列 单调递增,
因为 , 所以 ,
所以
所以
所以 ,所以 ,矛盾.
所以假设不成立,
所以数列 不是单调递增数列. ……….9分
(Ⅲ)若 ,
因为 , ,
所以
因为 ,又 ,所以 , ……….11分
所以 , ,
所以 ,
因为 ,所以
所以 ,即
因为 ,且
所以
所以
所以
即 ,所以 ,
又 所以 ,
此时 ,矛盾
所以不存在 ,使得 . ……….15分