文档内容
济宁市育才中学 2023 级高二年级下学期阶段性测试
数学试题
2025.02
(考试时间:120分钟 满分:150分)
一、单项选择题:本题共8小题,每小题5分,共40分在每小题给出的四个选项中,只有一
项是符合题目要求的.
1. 已知直线 与直线 互相平行,则点 在( )
.
A 圆 上 B. 圆 上
C. 圆 上 D. 圆 上
2. 已知 为抛物线 上一点,点 到 的焦点的距离为12,到 轴的距离为9,则
( )
A. 2 B. 3 C. 4 D. 6
3. 已知直线l与平面α垂直,直线l的一个方向向量为 =(1,-3,z),向量 =(3,-2,1)与平面α平行,
则z等于( )
A. 3 B. 6 C. -9 D. 9
4. 记 为数列 的前 项和,设甲: 为等差数列;乙: 为等差数列,则( )
A. 甲是乙的充分条件但不是必要条件
B. 甲是乙的必要条件但不是充分条件
的
C. 甲是乙 充要条件
D. 甲既不是乙的充分条件也不是乙的必要条件
的
5. 已知正方体 ,则不正确 是( )
A. 直线 与 所成的角为
B. 直线 与 所成的角为
C. 直线 与平面 所成的角为D. 直线 与平面ABCD所成的角为
6. 北京天坛的圜丘坛为古代祭天的场所,分上、中、下三层,上层中心有一块圆形石板(称为天心石),环
绕天心石砌9块扇面形石板构成第一环,向外每环依次增加9块,下一层的第一环比上一层的最后一环多
9块,向外每环依次也增加9块,已知每层环数相同,且下层比中层多729块,则三层共有扇面形石板(不
含天心石)( )
A. 3699块 B. 3474块 C. 3402块 D. 3339块
7. 若直线l与曲线y= 和x2+y2= 都相切,则l的方程为( )
A. y=2x+1 B. y=2x+ C. y= x+1 D. y= x+
8. 已知椭圆的方程为 ,上顶点为 ,左顶点为 ,设 为椭圆上一点,则 面积
的最大值为 .若已知 ,点 为椭圆上任意一点,则 的最小值为
( )
A. 2 B. C. 3 D.
二、多项选择题:本题共3小题,每小题6分,共18分.在每小题给出的四个选项中,有多项
符合题目要求全部选对得6分,部分选对得部分分,有选错的得0分.
9. 下列求导运算正确的是( )
A. B.C. D.
10. 已知双曲线 的左、右焦点分别为 , ,左、右顶点分别为 , ,P
为双曲线的左支上一点,且直线 与 的斜率之积等于3,则下列说法正确的是( )
A. 双曲线 的离心率为2
B. 若 ,且 ,则
C. 以线段 , 为直径的两个圆外切
在
D. 若点P 第二象限,则
11. 在长方体 中, , ,动点 在体对角线 上(含端点),
则下列结论正确的有( )
A. 当 为 中点时, 为锐角
B. 存在点 ,使得 平面
C. 的最小值D. 顶点 到平面 的最大距离为
三、填空题:本题共3小题,每小题5分,共15分.
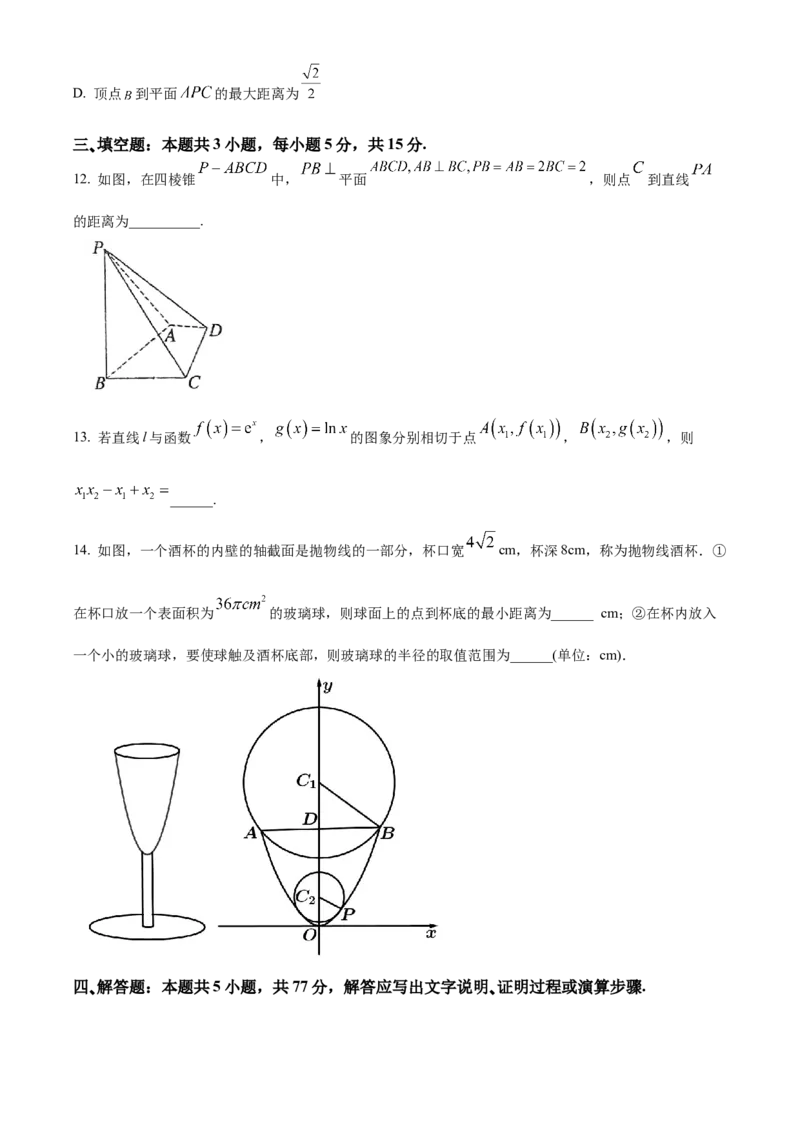
12. 如图,在四棱锥 中, 平面 ,则点 到直线
的距离为__________.
13. 若直线l与函数 , 的图象分别相切于点 , ,则
______.
14. 如图,一个酒杯的内壁的轴截面是抛物线的一部分,杯口宽 cm,杯深8cm,称为抛物线酒杯.①
在杯口放一个表面积为 的玻璃球,则球面上的点到杯底的最小距离为______ cm;②在杯内放入
一个小的玻璃球,要使球触及酒杯底部,则玻璃球的半径的取值范围为______(单位:cm).
四、解答题:本题共5小题,共77分,解答应写出文字说明、证明过程或演算步骤.15. 已知直线 ,直线 平分圆 .
的
(1)若 ,直线 与圆 交于 , 两点,求 周长;
(2)若直线 过定点 ,过点 作圆 的切线,求定点 的坐标及切线方程.
16. 设 是公比不为1的等比数列, 为 , 的等差中项.
(1)求 的公比;
(2)若 ,求数列 的前 项和.
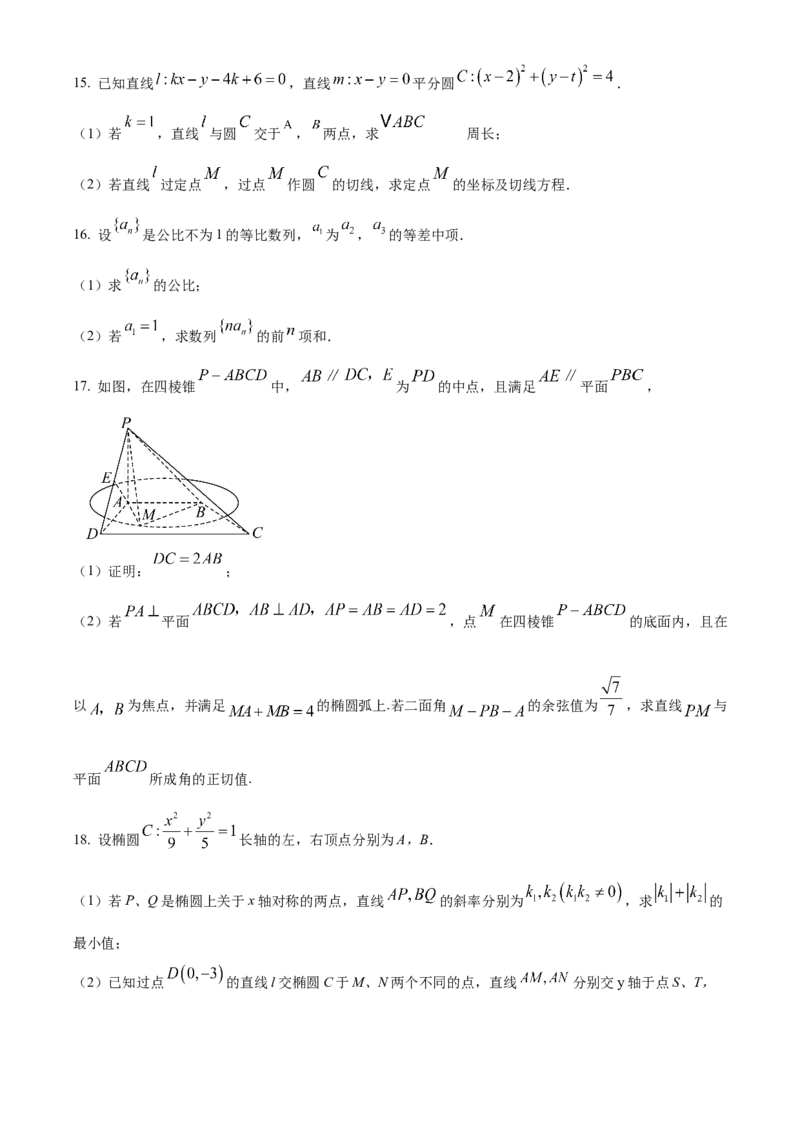
17. 如图,在四棱锥 中, 为 的中点,且满足 平面 ,
(1)证明: ;
(2)若 平面 ,点 在四棱锥 的底面内,且在
以 为焦点,并满足 的椭圆弧上.若二面角 的余弦值为 ,求直线 与
平面 所成角的正切值.
18. 设椭圆 长轴的左,右顶点分别为A,B.
(1)若P、Q是椭圆上关于x轴对称的两点,直线 的斜率分别为 ,求 的
最小值;
(2)已知过点 的直线l交椭圆C于M、N两个不同的点,直线 分别交y轴于点S、T,记 (O为坐标原点),当直线1的倾斜角 为锐角时,求 的取值范围.
19. 已知数列 的首项a=1,前n项和为S.设λ与k是常数,若对一切正整数n,均有
1 n
成立,则称此数列为“λ~k”数列.
(1)若等差数列 是“λ~1”数列,求λ的值;
(2)若数列 是“ ”数列,且a>0,求数列 的通项公式;
n
(3)对于给定的λ,是否存在三个不同的数列 为“λ~3”数列,且a≥0?若存在,求λ的取值范围;若
n
不存在,说明理由,