文档内容
高三数学 10 月考
一.单选题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合
题目要求的.
1. 复数 (i为虚数单位)复平面内对应的点位于( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
2. 设集合 , ,则 ( )
A. B. C. D.
3. 已知数列 满足 ,若 ,则 ( )
A. B. C. 12 D. 36
4. 已知向量 , ,若 ,则 ( )
A. -6 B. 0 C. D.
5. 遗忘曲线由德国心理学家艾宾浩斯研究发现,描述了人类大脑对新事物遗忘的规律,某同学利用信息技术拟合了
“艾宾浩斯遗忘曲线”,得到记忆率 与初次记忆经过的时间 (小时)的大致关系: ,则记忆率为20%
时经过的时间约为( )(参考数据: , )
A. 80小时 B. 90小时 C. 100小时 D. 120小时
6. 已知函数 ,若正实数 , 满足 ,则 的最小值为( )
A. B. 7 C. D.
7. 已知 为 锐角, ,则 ( )
公众号:黑洞视角A. B. C. D.
8. 已知函数 ,若对任意的 , 恒成立,则实数 的取值范围为( )
A. B. C. D.
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目
要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
9. 下列说法正确的是( )
的
A. 若函数 定义域为 ,则函数 的定义域为
B. 的最大值为
C. 的图象关于 成中心对称
D. 的递减区间是
10. 已知等比数列 的前 项和为 ,公比 , ,则( )
A. 一定是递增数列 B. 可能是递增数列也可能是递减数列
C. 、 、 仍成等比 D. ,
.
11 已知 则( )
A. B. C. D.
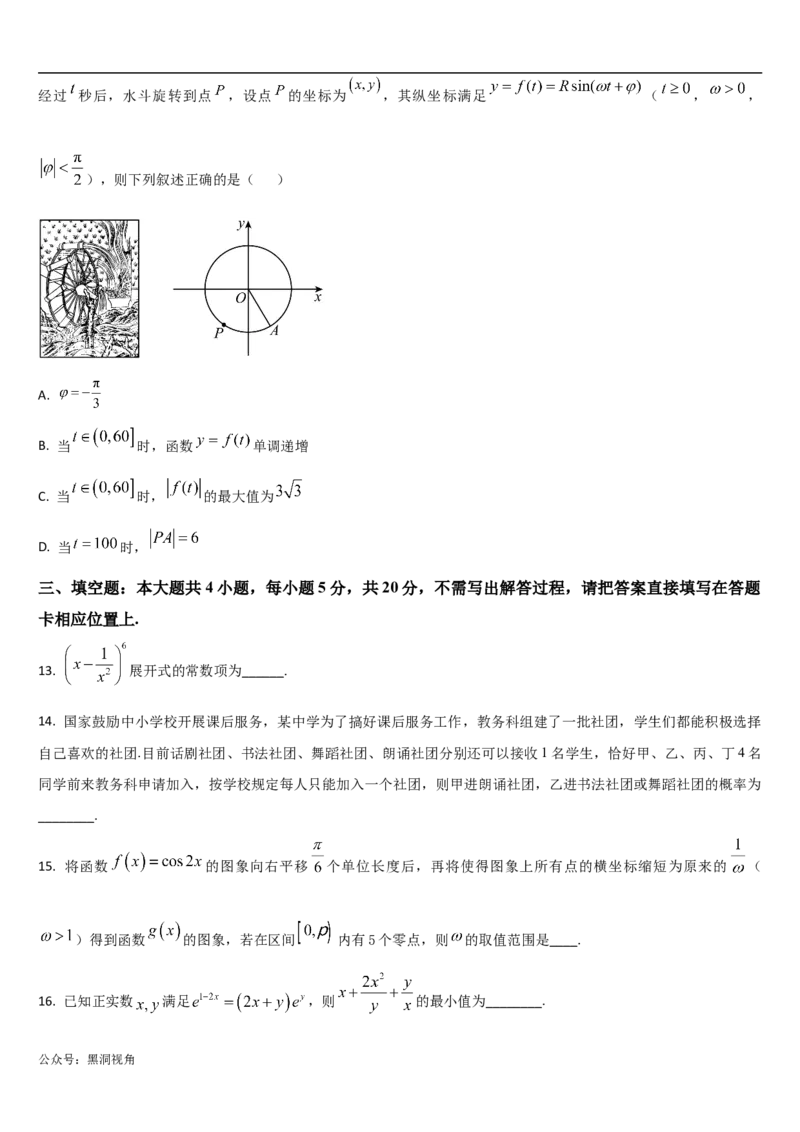
12. 水车在古代是进行灌溉引水的工具,亦称“水转筒车”,是一种以水流作动力,取水灌田的工具.据史料记载,水车
发明于隋而盛于唐,距今已有1000多年的历史,是人类的一项古老的发明,也是人类利用自然和改造自然的特征.如
图是一个半径为 的水车,一个水斗从点 出发,沿圆周按逆时针方向匀速旋转,且旋转一周用时120秒.
公众号:黑洞视角经过 秒后,水斗旋转到点 ,设点 的坐标为 ,其纵坐标满足 ( , ,
),则下列叙述正确的是( )
A.
B. 当 时,函数 单调递增
C. 当 时, 的最大值为
D. 当 时,
三、填空题:本大题共 4小题,每小题5分,共20分,不需写出解答过程,请把答案直接填写在答题
卡相应位置上.
13. 展开式的常数项为______.
14. 国家鼓励中小学校开展课后服务,某中学为了搞好课后服务工作,教务科组建了一批社团,学生们都能积极选择
自己喜欢的社团.目前话剧社团、书法社团、舞蹈社团、朗诵社团分别还可以接收1名学生,恰好甲、乙、丙、丁4名
同学前来教务科申请加入,按学校规定每人只能加入一个社团,则甲进朗诵社团,乙进书法社团或舞蹈社团的概率为
________.
15. 将函数 的图象向右平移 个单位长度后,再将使得图象上所有点的横坐标缩短为原来的 (
)得到函数 的图象,若在区间 内有5个零点,则 的取值范围是____.
16. 已知正实数 满足 ,则 的最小值为________.
公众号:黑洞视角四、解答题:本题共6小题,解答应写出文字说明、证明过程或演算步骤.
17. 已知锐角 中,角A,B,C的对边分别为a,b,c,若 .
(1)证明: ;
(2)若 ,求 的取值范围.
18. 已知数列 的前 项和为 ,且 .
(1)求数列 的通项公式;
(2)设 ,求数列 的前 项和 .
19. 某专营店统计了最近 天到该店购物的人数 和时间第 天之间的数据,列表如下:
(1)由表中给出的数据,判断是否可用线性回归模型拟合人数 与时间 之间的关系?(若 ,则认为线性相
关程度高,可用线性回归模型拟合;否则,不可用线性回归模型拟合.计算 时精确到 )
(2)该专营店为了吸引顾客,推出两种促销方案:方案一,购物金额每满 元可减 元;方案二,购物金额超过
元可抽奖三次,每次中奖的概率均为 ,且每次抽奖互不影响,中奖一次打 折,中奖两次打 折,中奖三次打
折.某顾客计划在此专营店购买一件价值 元的商品,请从实际付款金额的数学期望的角度分析,选哪种方案更
优惠?
公众号:黑洞视角参考数据: .附:相关系数 .
20. 如图,在四面体 中, 平面 , 是 的中点, 是 的中点, 是线段 上的一点,
.
(1)若 ,证明: 平面 ;
(2)若 ,且二面角 为直二面角,求实数 的值.
21. 已知函数 ,函数 与 关于点 中心对称.
(1)求 的解析式;
(2)若方程 有两个不等的实根 , ,且 ,求a的值.
.
22 已知函数 .
(1)若 ,求 的极值.
(2)若方程 在区间 上有解,求实数 的取值范围.
公众号:黑洞视角DADCC DCB 9AC 10BCD 11BCD 12AD
13 15 14
15 16 2
17(1)因为 ,由正弦定理得 ,
所以 ,
所以 ,
而 ,则 或 ,
即 或 (舍去),故 .
(2)
18(1) ,
(2) , .
19
(1)可以, 解: , ,
所以, ,
, ,
公众号:黑洞视角所以, ,
所以, 与 的线性相关性很强,故可用线性回归模型拟合人数 与时间 之间的关系.
(2)方案二更优惠,解:设方案一的实际付款金额为 元,方案二的实际付款金额为 元,
由题意可知, (元),
的可能取值有 、 、 、 ,
, ,
, ,
所以, ,
所以,方案二更优惠.
20(1)证明:取 的中点 ,连接 、 ,如下图所示:
因为 为 的中点, 为 的中点,则 ,所以, ,
又因为 ,即 ,所以, ,则 ,
公众号:黑洞视角因为 平面 , 平面 ,所以, 平面 ,
又因为 为 的中点,则 ,
因为 平面 , 平面 ,所以, 平面 ,
因为 , 、 平面 ,所以,平面 平面 ,
因为 平面 ,故 平面 .
(3)
21(1)
(2)
22(1)极小值为 ,无极大值
(2)
公众号:黑洞视角