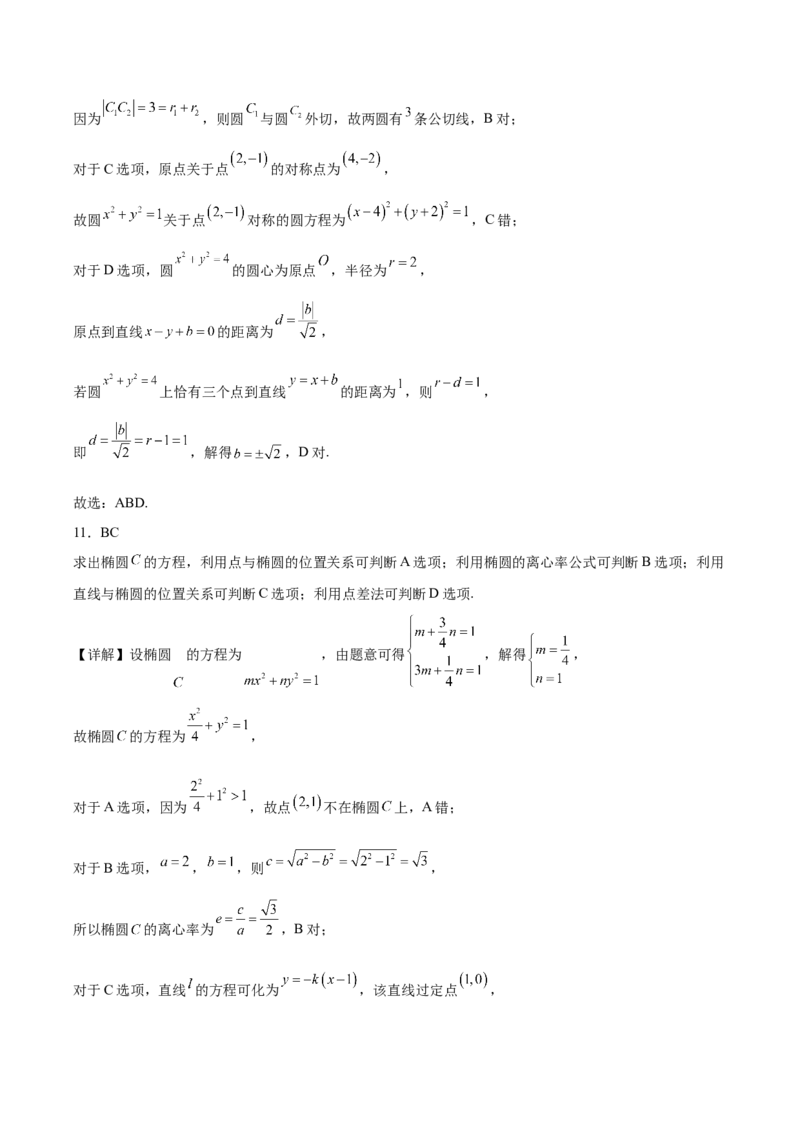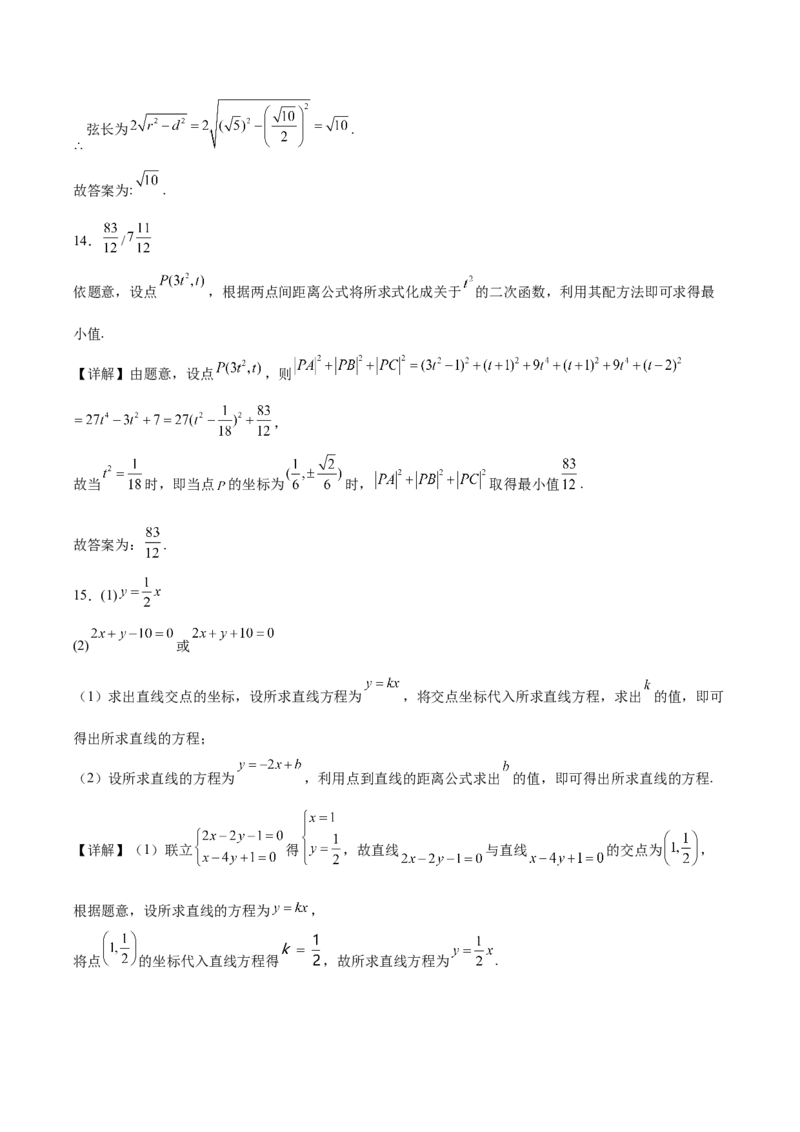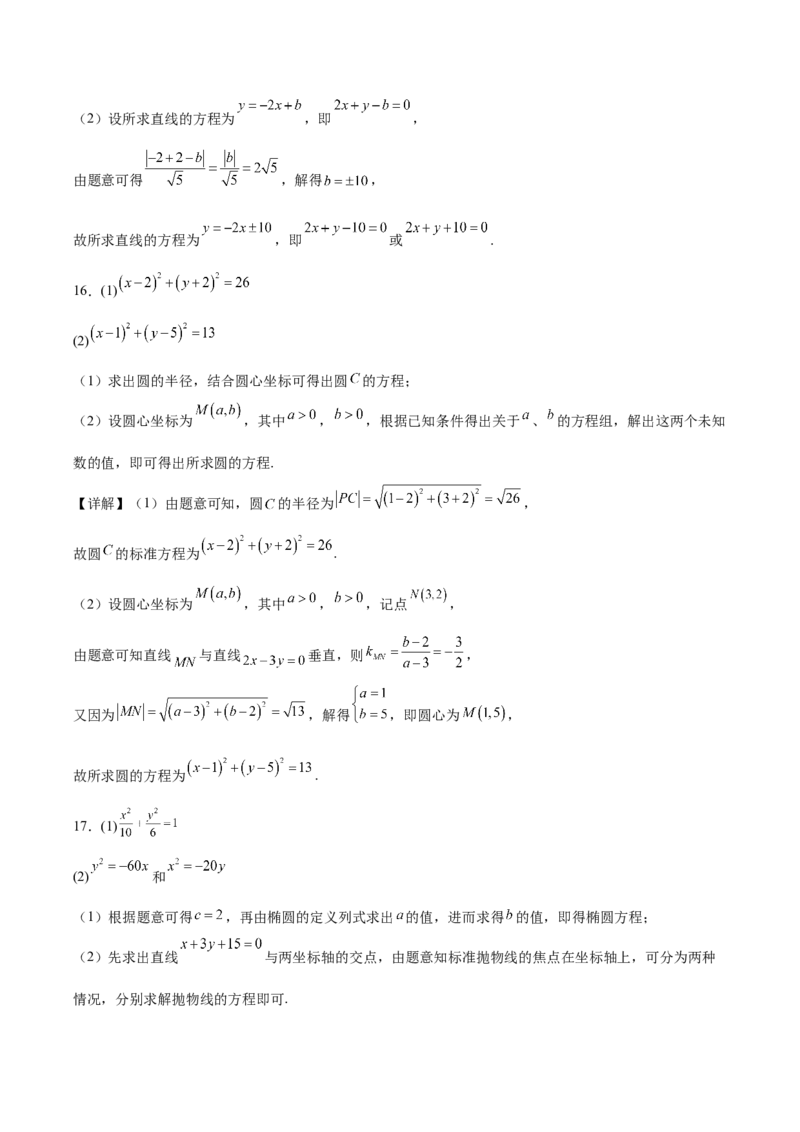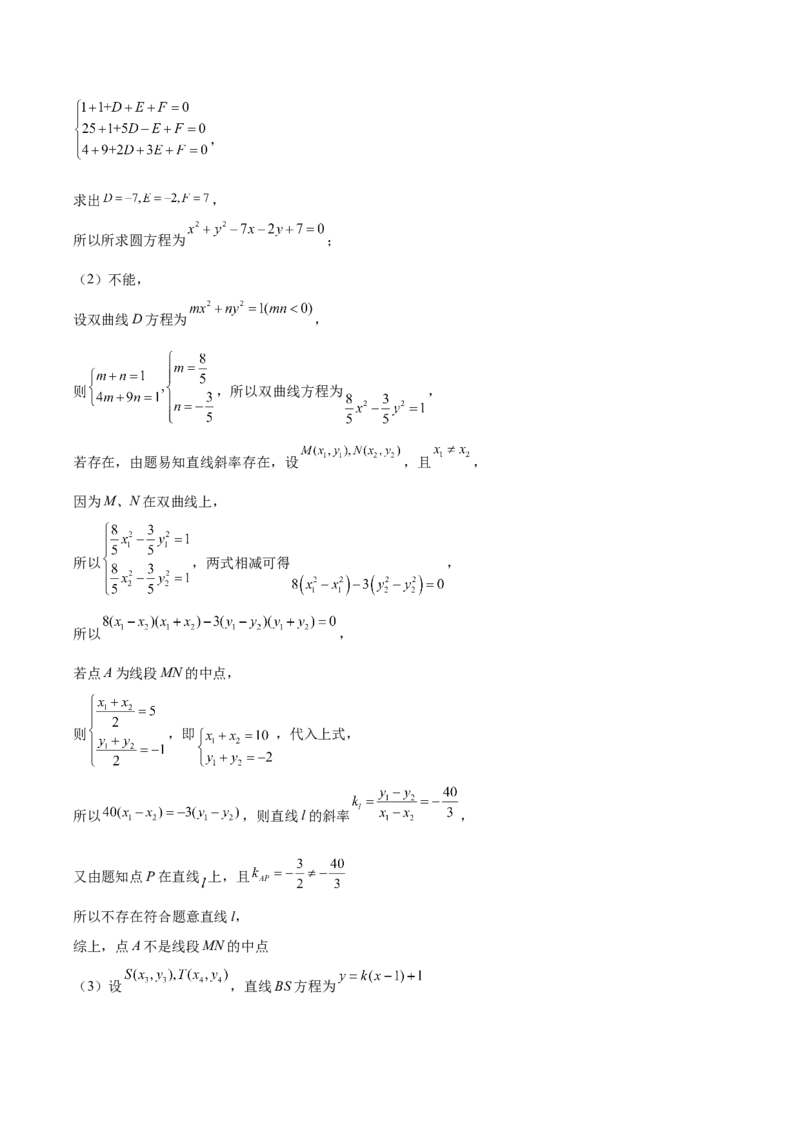文档内容
2025-2026学年高二上学期11月期中联考
数学试题
一、单选题
1.直线 的斜率为( )
A.1 B.2 C. D.
2.已知 , ,则线段 的中点坐标为( )
A.(1,4) B.(2,1) C.(2,8) D.(4,2)
3.抛物线 的焦点坐标为( )
A. B.
C. D.
4.双曲线 的实轴长为( )
A.4 B.6 C.8 D.10
5.已知圆 和圆 ,则 与 的位置关系是( )
A.外切 B.内切 C.相交 D.外离
6.如果椭圆 上一点P到焦点 的距离等于2,则点P到另一个焦点 的距离为( )
A.6 B.4 C.3 D.2
7.过圆 上一点 作圆的切线 则 的方程为( )
A. B. C. D.
8.已知过椭圆 的左焦点 的直线与椭圆交于不同的两点A,B,与y轴交于点C,点C,F是线段AB的三等分点,则该椭圆的离心率为( )
A. B. C. D.
二、多选题
9.下列说法正确的是( )
A.直线 在 轴, 轴上的截距分别为3,2;
B.两条平行直线 与 的距离为
C.直线 恒过定点
D.过点 ,且与直线 垂直的直线方程为
10.下列说法正确的是( )
A.已知圆的方程为 ,则此圆的圆心坐标为
B.两圆 与 的公切线有 条
C.圆 关于点 对称的圆方程为
D.若圆 上恰有三个点到直线 的距离为 ,则
11.平面直角坐标系中椭圆 的中心为原点,焦点在坐标轴上,点 、 均在椭圆 上,则
( )
A.点 在椭圆 上
B.椭圆 的离心率为
C.直线 与椭圆 相交D.若椭圆 上弦 的中点坐标为 ,则直线 的斜率为
三、填空题
12.双曲线 的渐近线方程为 .
13.已知直线l: 和圆心为C的圆 ,则直线l被圆C截得的弦长为 .
14.已知 , , 三点,点P在抛物线 上运动,则 的最小值
为 .
四、解答题
15.分别求满足下列条件的直线方程.
(1)过原点,且经过直线 与直线 的交点;
(2)斜率为 ,且到点 的距离为 .
16.分别求满足下列条件的圆的方程
(1)过点 ,圆心为 ;
(2)圆心在第一象限,半径为 ,且与直线 相切于点 .
17.分别求适合下列条件的圆锥曲线的标准方程.
(1)两个焦点坐标分别是 ,并且经过点 的椭圆方程;
(2)焦点在直线 上的抛物线方程.
18.已知椭圆 , 、 分别是左、右焦点, 是椭圆 上一点, 的最大值为
,当 为椭圆上顶点时,直线 的倾斜角为 .(1)求椭圆 的标准方程;
(2)过点 作直线 交于椭圆 、 两点
( )若直线 的倾斜角为 ,求线段 的长;
( )求 的面积最大值.
19.已知 , , 三点
(1)求 外接圆方程;
(2)若过点 的直线l与中心在原点,过B,C两点的双曲线D相交于M,N两点,A能否是线段MN的
中点?请说明理由?
(3)S,T是双曲线D上的两个动点,且直线BS,BT的斜率互为相反数,证明直线ST的斜率为定值.题号 1 2 3 4 5 6 7 8 9 10
答案 B A C C A A C D ACD ABD
题号 11
答案 BC
1.B
直线方程一般式转化为斜截式.
【详解】 化简得 ,所以斜率为2.
故选:B.
2.A
用中点坐标公式即可求解.
【详解】设线段 的中点坐标为 ,则 ,
即 ,则线段 的中点坐标为 .
故选:A.
3.C
由标准方程可确定焦点位置和焦点横坐标,从而得到结果.
【详解】由抛物线方程知其焦点在 轴上且 , 其焦点坐标为 .
故选:C.
4.C
由双曲线的标准方程可以直接得出答案.
【详解】双曲线 中, ,
则实轴长 .
故选:C
5.A
由圆的方程可确定两圆的圆心和半径,由两圆圆心距与两圆半径的关系可判断出位置关系.
【详解】由圆 方程知:圆心 ,半径 ;由 ,得 ,
所以圆心 ,半径 ;
圆心距 ,所以圆 与圆 外切.
故选:A
6.A
根据椭圆的定义可以解.
【详解】由椭圆的定义得: ,所以 .
故选:A
7.C
先求圆心C, 和切线垂直,求出切线斜率,然后求直线方程.
【详解】由题意得:圆心 ,所以 ,且 ,解得 .
所以直线 的方程为: ,化简得: .
故选:C
8.D
取椭圆的右焦点为点 ,连接 ,过点 作 轴于点 ,利用三角形中位线定理和相似形求出点
的坐标,代入椭圆方程求出 的值,即可求得离心率.
【详解】如图,取椭圆的右焦点为点 ,连接 ,则 ,
因为点C,F是线段AB的三等分点,则C为 的中点,而O为 的中点,
可得 ,因 ,故 ,将 代入 ,可得 ,
根据椭圆对称性,不妨取点 ,过点 作 轴于点 ,易得 ,
可得 ,因 ,则 ,即得 ,
代入 可得 ,又 ,代入解得 ,
故该椭圆的离心率为 .
故选:D.
9.ACD
A选项,由直线截距式进行判断;B选项,将直线变形,利用两平行线间距离公式直接求解;C选项,由
直线点斜式进行判断;D选项,设出直线方程,利用待定系数法进行求解.
【详解】A选项,由直线截距式可知 在 轴, 轴上的截距分别为3,2,A正确;
B选项,直线 ,即 ,
与 的距离为 ,B错误;
C选项,由直线点斜式可知 恒过定点 ,C正确;
D选项,设直线方程为 ,将 代入可得 ,
解得 ,故直线方程为 ,D正确.
故选:ACD
10.ABD
将圆的方程化为标准方程,可判断A选项;判断两圆的位置关系,可判断B选项;求出对称圆的方程,可
判断C选项;根据直线与圆的位置关系求出 的值,可判断D选项.
【详解】对于A选项,圆 的标准方程为 ,其圆心为 ,A对;
对于B选项,圆 的圆心为 ,半径为 ,圆 的圆心为 ,半径为 ,因为 ,则圆 与圆 外切,故两圆有 条公切线,B对;
对于C选项,原点关于点 的对称点为 ,
故圆 关于点 对称的圆方程为 ,C错;
对于D选项,圆 的圆心为原点 ,半径为 ,
原点到直线 的距离为 ,
若圆 上恰有三个点到直线 的距离为 ,则 ,
即 ,解得 ,D对.
故选:ABD.
11.BC
求出椭圆 的方程,利用点与椭圆的位置关系可判断A选项;利用椭圆的离心率公式可判断B选项;利用
直线与椭圆的位置关系可判断C选项;利用点差法可判断D选项.
【详解】设椭圆 的方程为 ,由题意可得 ,解得 ,
故椭圆 的方程为 ,
对于A选项,因为 ,故点 不在椭圆 上,A错;
对于B选项, , ,则 ,
所以椭圆 的离心率为 ,B对;
对于C选项,直线 的方程可化为 ,该直线过定点 ,因为 ,则点 在椭圆 内,故直线 与椭圆 相交,C对;
对于D选项,若 的斜率不存在,则线段 的中点在 轴上,不合乎题意,
所以直线 的斜率存在,设点 、 ,由题意可得 ,
因为 ,两个等式作差得 ,
所以 ,故 ,D错.
故选:BC.
12.
求出 、 的值,即可得出双曲线的渐近线方程.
【详解】在双曲线 中, , ,
所以双曲线 的渐近线方程为 .
故答案为: .
13.
先求圆心到直线的距离 ,再计算 即可求出弦长.
【详解】圆 化为标准方程为: ,
圆心 , ,
,弦长为 .
故答案为: .
14. /
依题意,设点 ,根据两点间距离公式将所求式化成关于 的二次函数,利用其配方法即可求得最
小值.
【详解】由题意,设点 ,则
,
故当 时,即当点 的坐标为 时, 取得最小值 .
故答案为: .
15.(1)
(2) 或
(1)求出直线交点的坐标,设所求直线方程为 ,将交点坐标代入所求直线方程,求出 的值,即可
得出所求直线的方程;
(2)设所求直线的方程为 ,利用点到直线的距离公式求出 的值,即可得出所求直线的方程.
【详解】(1)联立 得 ,故直线 与直线 的交点为 ,
根据题意,设所求直线的方程为 ,
将点 的坐标代入直线方程得 ,故所求直线方程为 .(2)设所求直线的方程为 ,即 ,
由题意可得 ,解得 ,
故所求直线的方程为 ,即 或 .
16.(1)
(2)
(1)求出圆的半径,结合圆心坐标可得出圆 的方程;
(2)设圆心坐标为 ,其中 , ,根据已知条件得出关于 、 的方程组,解出这两个未知
数的值,即可得出所求圆的方程.
【详解】(1)由题意可知,圆 的半径为 ,
故圆 的标准方程为 .
(2)设圆心坐标为 ,其中 , ,记点 ,
由题意可知直线 与直线 垂直,则 ,
又因为 ,解得 ,即圆心为 ,
故所求圆的方程为 .
17.(1)
(2) 和
(1)根据题意可得 ,再由椭圆的定义列式求出 的值,进而求得 的值,即得椭圆方程;
(2)先求出直线 与两坐标轴的交点,由题意知标准抛物线的焦点在坐标轴上,可分为两种
情况,分别求解抛物线的方程即可.【详解】(1)由于椭圆的焦点在x轴上,可设其标准方程为 .由题意, ,
根据椭圆的定义, ,解得 ,
所以 .
故所求椭圆的标准方程为 .
(2)因为直线 与两坐标轴的交点分别为 和 ,即抛物线的焦点坐标可以是
和 ,
当抛物线的焦点为 ,其方程形如 ,
则由 可得 ,此时抛物线的方程为 ;
当抛物线的焦点为 时,其方程形如 ,
则由 可得 ,此时抛物线的方程为 .
综上,可得抛物线的方程为 和 .
18.(1)
(2)(i) ;(ii) .
(1)根据题设条件得出关于 、 、 的方程组,解出这三个量的值,即可得出椭圆 的标准方程;
(2)(i)将直线 的方程与椭圆方程联立,列出韦达定理,利用弦长公式与韦达定理可求得 的值;
(ii)设直线 的方程为 ,将该直线的方程与椭圆方程联立,列出韦达定理,利用三角形的面
积公式、韦达定理以及对勾函数的单调性可求得 的面积最大值.【详解】(1)设点 ,其中 ,则 ,
,
故 的最大值为 ,
①
当点 为上顶点 时, ,
②
又因为 ,由 得 , , ,
③ ①②③
所以椭圆 的标准方程为 .
(2)设 、 ,易知点 、 ,
(i)由题意可知直线 的方程为 ,
联立 得 , ,
由韦达定理可得 , ,
所以 .
(ii)易知直线 与 轴不重合,设直线 的方程为 ,联立 得 , ,
由韦达定理可得 , ,
所以 ,
所以三角形的面积为
令 ,则函数 在 上为增函数,
故当 时,即当 时, 取最大值,且 .
19.(1)
(2)不是,理由见解析.
(3)证明见解析
(1)设圆的一般方程列方程组计算求解;
(2)代入点得出双曲线方程 ,再应用点差法计算求解结合点A为线段MN的中点得出矛盾;
(3)联立方程计算得出 ,再应用斜率公式计算求解.
【详解】(1)设圆方程为 ,,
求出 ,
所以所求圆方程为 ;
(2)不能,
设双曲线D方程为 ,
则 ,所以双曲线方程为 ,
若存在,由题易知直线斜率存在,设 ,且 ,
因为M、N在双曲线上,
所以 ,两式相减可得 ,
所以 ,
若点A为线段MN的中点,
则 ,即 ,代入上式,
所以 ,则直线l的斜率 ,
又由题知点P在直线 上,且
所以不存在符合题意直线l,
综上,点A不是线段MN的中点
(3)设 ,直线BS方程为则 ,
所以 ,
所以
得 ,
同理 ,