山东省日照市2025届高三上学期11月期中校际联合考试数学答案_2024-2025高三（6-6月题库）_2024年11月试卷_1126山东省日照市2025届高三上学期11月期中校际联合考试

参照秘密级管理 启用前 试卷类型：A ★ 2022 级高三上学期校际联合考试 数学答案 2024.11 一、选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求的。 1-4AABB 5-8DBCC 二、选择题：本题共3小题，每小题6分，共18分。在每小题给出的选项中，有多项符合题目要求。全部选对的 得6分，部分选对的得部分分，有选错的得0分。 9.ACD 10.AC 11.ABD 三、填空题：本题共3小题，每小题5分，共15分。  3  12．【答案】192 13.【答案】2 14．【答案】   0,    3  四、解答题：本题共5小题，共77分。解答应写出文字说明，证明过程或演算步骤。 15.【解析】（1）当n1时，a a 1 a a 12， 1 2 2 1 1 1 1 a  a  a  a a 1 1 2 2 3 3 n n n1 1 1 1 当n2时，a  a  a  a a 1. 1 2 2 3 3 n1 n1 n 1 a n1 两式相减得： a a a  n1  . ……………………3分 n n n1 n a n n a a a a 3 4 5 n a n 所以： 3  4 5 n      n   a n，………………5分 a a a a 2 3 4 n 1 a 2 n 2 3 4 n1 2 当n1时，上式也成立. ……………………6分 所以数列a 的通项公式为：a n ……………………7分 n n （2）因为T 121222323n2n, n 2T  122223324n12nn2n1 n 两式相减得：T 222232n n2n12n12n2n11n2n12， n 所以T n12n12 …………………………13分 n 16．【解析】（1）∵2sinA3sin2C，∴sinA3sinCcosC， a2b2c2 由正余弦定理得a3c ①， ……………………3分 2ab 又c2b②由①②得，a2b3b  a2b24b2 ， 9 3 2 a 3 2 ∴a2  b2 a b，∴  ……………………7分 2 2 b 2 3 2 b （2）由（1）得， sinA a 2 2，……………………9分 cosC    3sinC 3c 6b 4 高三数学试题答案 第 1 页 共4页 {#{QQABRYAEogCIABBAAAhCEQXyCkIQkgCCCSgGQEAAoAAAyRFABCA=}#}9 b2b24b2 （或由余弦定理得 a2b2c2 2 2 ） cosC    2ab 3 2b2 4 14 ∵C为三角形内角，∴sinC ， ……………………10分 4 1 1 3 2 14 3 7 ∴ABC的面积S  absinC  b2   ， 2 2 2 4 2 ∴b2， ……………………12分 1 3 7 设AB边上的高为h，则ABC的面积S  chbh ， 2 2 3 7 3 7 ∴h ，即AB边上的高为 . …………………15分 4 4 17．【解析】（1）由题知AB面BEC,EC 面BEC，则ABEC， 由BC为底面圆的直径，则ECBE， 由BEABB，BE,AB面ABE，EC 面ABE， 又∵BM 面ABE，∴EC BM ， 又BM  AC,ACEC C，AC,EC面AEC，BM 面AEC， …………………4分 （2）由（1）知，BM 面AEC，又∵AE面AEC，故BM  AE, 3 由AB BC 2BE，得BE  AE, 3 3 AE BE ( AE)2 ABE  BME ，  , BE2 3 1 BE ME ME    AE AE AE 3  2 AM  AE ，故MN// EC,EC面BEC,MN 面BEC, 3 ∴MN //面BEC，又面BEC面BMN l，MN 面BMN，∴MN//l.………………8分 （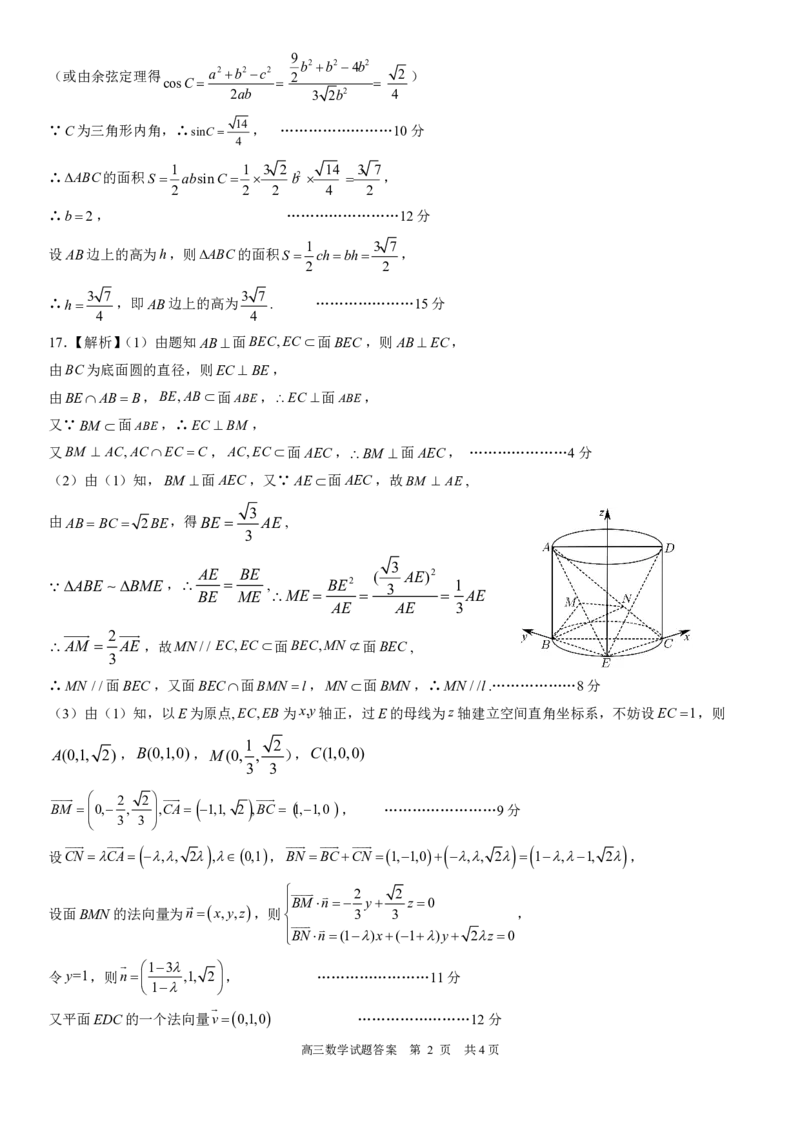3）由（1）知，以E为原点,EC,EB为x,y轴正，过E的母线为z轴建立空间直角坐标系，不妨设EC1，则 1 2 A(0,1, 2)，B(0,1,0)，M(0, , ），C(1,0,0) 3 3  B  M    0, 2 , 2 ,C  A    1,1, 2  ,  B  C   1,1,0 ， ……………………9分    3 3  设C  N  C  A    ,, 2  ,0,1，  B  N    B  C  C  N  1,1,0  ,, 2    1,1, 2  ，   2 2 r BMn y z0 设面BMN的法向量为nx,y,z，则 3 3 ，   BNn(1)x(1)y 2z0  13  令y=1，则n ,1, 2， ……………………11分  1   又平面EDC的一个法向量v0,1,0 ……………………12分 高三数学试题答案 第 2 页 共4页 {#{QQABRYAEogCIABBAAAhCEQXyCkIQkgCCCSgGQEAAoAAAyRFABCA=}#}  1 1 cos cos nv   设平面BMN与平面DEC的夹角为， 13 2 ， ( )2 3 1 1 解得0或 ，其中0时N,C重合，不合题意，……………………14分 2 π 1 故当平面BMN与平面DEC夹角为 时 ，此时N 为AC中点. …………………15分 3 2 18．【解析】（1）函数 f(x)的定义域为(0，)， 2a 1 若函数 f(x)在(0，)上是减函数，则 f(x)2 2ax0在(0，)上恒成立，即a(x )1在(0，) x x 1 a 上恒成立，即 1 在(0，)上恒成立……………2分 x x 1 1 又x0时，(x )2 x 2，当且仅当x1时等号成立， x x 1 所以a ； …………………………4分 2 2a （2）由 f(x)0，得2 2ax0， x 原方程可化为：ax2xa0①，由题意x，x 是方程①的两个不同的正实根， 1 2 Δ14a2＞0  1 所以 1 ，解得0a ， ……………………6分  ＞0 2  a 2 1 1 ∴ f(x) f(x )2(x x )2aln(xx )a(x2 x2 )2 a( 2)2 2a2，………8分 1 2 1 2 1 2 1 2 a a2 a 1 1 1 1 因为0a ，且函数y2a 2在(0，)上单调递减，所以2a 210， 2 a 2 a 所以 f(x) f(x )0； ……………………9分 1 2 （3）由题意可知，a 1时， f(x)2x2lnxx21， 令g(x) f( x)x 2 x lnx1 ，则 f(1)0，g(1)1， 因为g'(x) x1 ，所以当x(0,1)时，g'(x)0，所以函数y g(x)在区间(0,1)上单调递减， x 当x(1,)时，g'(x)0，所以函数y g(x)在区间(1,)上单调递增，…………11分 因为0a 1，a  f ( a )a  g(a ) ，所以a g(a)g(1)1，a g(a )g(1)1， 1 n1 n n n 2 1 3 2 以此类推，当n1时，a g(a )g(1)1，即n2时，a 1……………………13分 n1 n n 由已知 f( x)2 xlnxx1，令h(x) f( x)2 xlnxx1，  12 3 1 1 1   x 2    4 ，故函数yh(x) f( x)在区间(0,)上单调递减， h'(x)2  1   0 2 x x x 高三数学试题答案 第 3 页 共4页 {#{QQABRYAEogCIABBAAAhCEQXyCkIQkgCCCSgGQEAAoAAAyRFABCA=}#}由于当n2时， a 1，所以h(a )h(1)0，又h(a ) f( a )a a ， n n n n n1 n 所以a a 0，从而 a  a ， ………………15分 n1 n n1 n 所以 f( a ) f( a ) ，即a a a a ，故a a 2a . ……………………17分 n1 n n2 n1 n1 n n n2 n1 19．【解析】（1）0，1，2，1，0和0，1，0，1，0 ……………………4分 （2）若E数列A 是等差数列，因为|a a |1(k 1，2，，n1)， n k1 k 所以公差只能为1或-1 ，又因为a 2025,n2021， 1 所以a 5或4045，所以必要性不成立； ……………………6分 2021 当a 5时，由于a a 1，a a 1，…，a a 1， 2021 2021 2020 2020 2010 2 1 累加可得a a (1)20202020， 2021 1 即a a 20205，当且仅当a a a a a a 1，a 5，所以 2021 1 2021 2020 2020 2019 2 1 2021 a a 10k 1,2,,2020为同一常数， k1 k 所以数列A 是等差数列，所以充分性成立. ……………………8分 n 所以， p是q的充分不必要条件. ……………………9分 （3）令c a a k 1,2,n1，则c 1，a a c ． k k1 k k k1 k k 因为a a c ，a a c a c c ，……,a a c c c ， 2 1 1 3 2 2 1 1 2 n 1 1 2 n1 所以SA na n1c n2c n3c c n 1 1 2 3 n1 n1n211c n11c n21c  1 2 n1 nn1  2   1c 1 n1 1c 2 (n2）  1c n1   因为c 1，所以1c 为偶数k 1,2,n1，所以（1c )n11c n21c 为偶数． k k 1 2 n1 nn1 所以要使SA 0，必须使 为偶数，即4整除nn1，……………………11分 n 2 亦即n4m或n4m1  mN* ． 当n4m  mN* 时，取a a 0，a 1，a 1k 1,2,m，此时存在E数列A 使得a 0，SA 0； 4k1 4k3 4k2 4k n 1 n （A 不唯一） ……………………13分 n 当n4m1  mN* 时，取a a 0，a 1，a 1，a 0k 1,2,m，此时存在E数列A 使得 4k1 4k3 4k2 4k 4k1 n a 0，SA 0．（A 不唯一）……………………15分 1 n n 当n4m2，n4m3mN时，nn1不能被4整除，所以此时不存在E数列A 使得有a 0， n 1 SA 0． ……………………17分 n 高三数学试题答案 第 4 页 共4页 {#{QQABRYAEogCIABBAAAhCEQXyCkIQkgCCCSgGQEAAoAAAyRFABCA=}#}