文档内容
鹰潭市 2024 届高三第一次模拟考试
数学试卷
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共4页.时间120分钟.满分150
分.
第Ⅰ卷选择题
单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项
是符合题目要求的,请将正确答案的序号填涂在答题卡上.
1. 若复数 满足 ,则 ( )
A. B. C. D.
2. 已知集合 ,集合 ,若 ,则 的取值范围为( )
A. B. C. D.
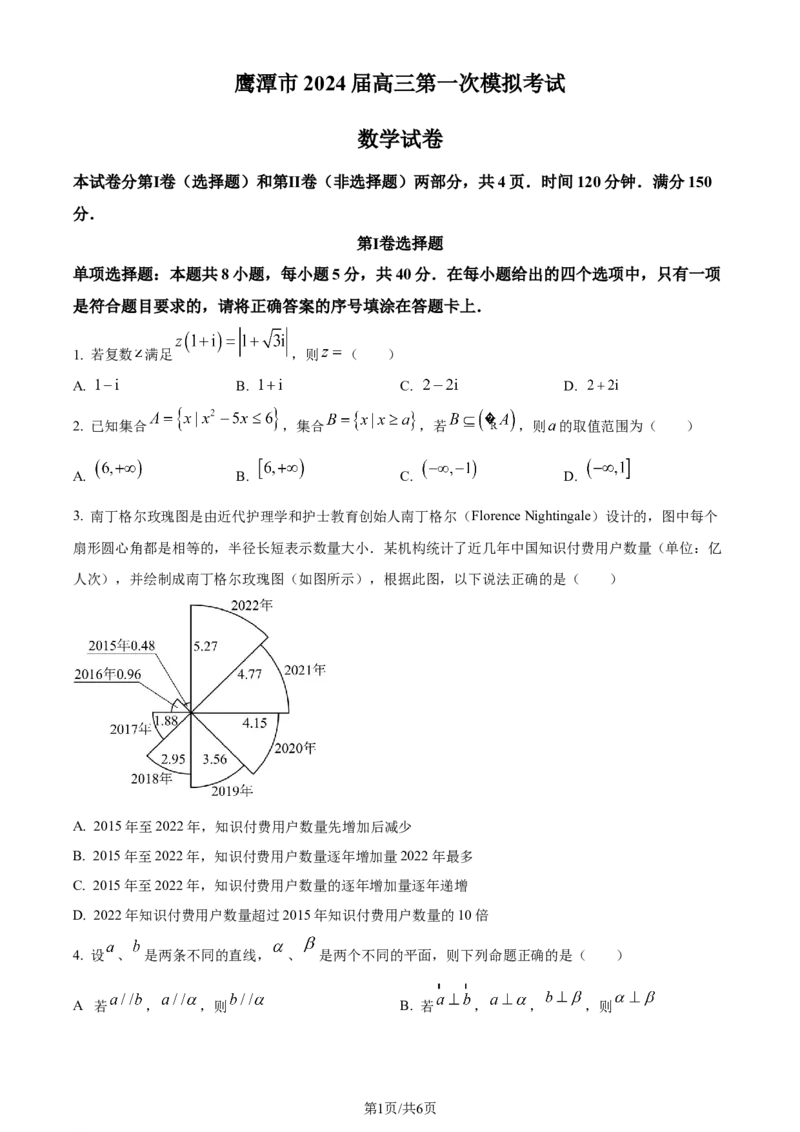
3. 南丁格尔玫瑰图是由近代护理学和护士教育创始人南丁格尔(Florence Nightingale)设计的,图中每个
扇形圆心角都是相等的,半径长短表示数量大小.某机构统计了近几年中国知识付费用户数量(单位:亿
人次),并绘制成南丁格尔玫瑰图(如图所示),根据此图,以下说法正确的是( )
A. 2015年至2022年,知识付费用户数量先增加后减少
B. 2015年至2022年,知识付费用户数量逐年增加量2022年最多
C. 2015年至2022年,知识付费用户数量的逐年增加量逐年递增
D. 2022年知识付费用户数量超过2015年知识付费用户数量的10倍
4. 设 、 是两条不同的直线, 、 是两个不同的平面,则下列命题正确的是( )
.
A 若 , ,则 B. 若 , , ,则
第1页/共6页
学科网(北京)股份有限公司C. 若 , ,则 D. 若 , ,则
5. 某单位为了解职工体重情况,采用分层随机抽样的方法从800名职工中抽取了一个容量为80的样本.
其中,男性平均体重为64千克,方差为151;女性平均体重为56千克,方差为159,男女人数之比为 ,
则单位职工体重的方差为( )
A. 166 B. 167 C. 168 D. 169
6. 已知 , , =( )
.
A B. C. 3 D.
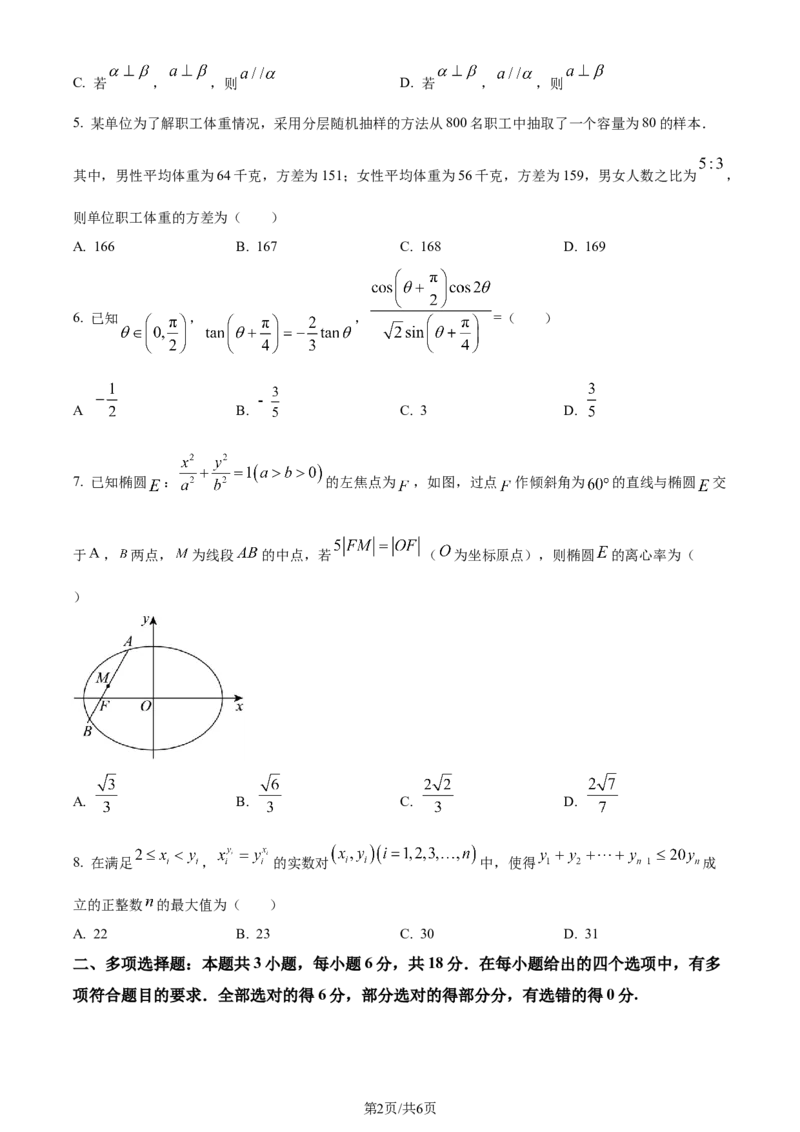
7. 已知椭圆 : 的左焦点为 ,如图,过点 作倾斜角为 的直线与椭圆 交
于 , 两点, 为线段 的中点,若 ( 为坐标原点),则椭圆 的离心率为(
)
A. B. C. D.
8. 在满足 , 的实数对 中,使得 成
立的正整数 的最大值为( )
A. 22 B. 23 C. 30 D. 31
二、多项选择题:本题共3小题,每小题6分,共18分.在每小题给出的四个选项中,有多
项符合题目的要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
第2页/共6页
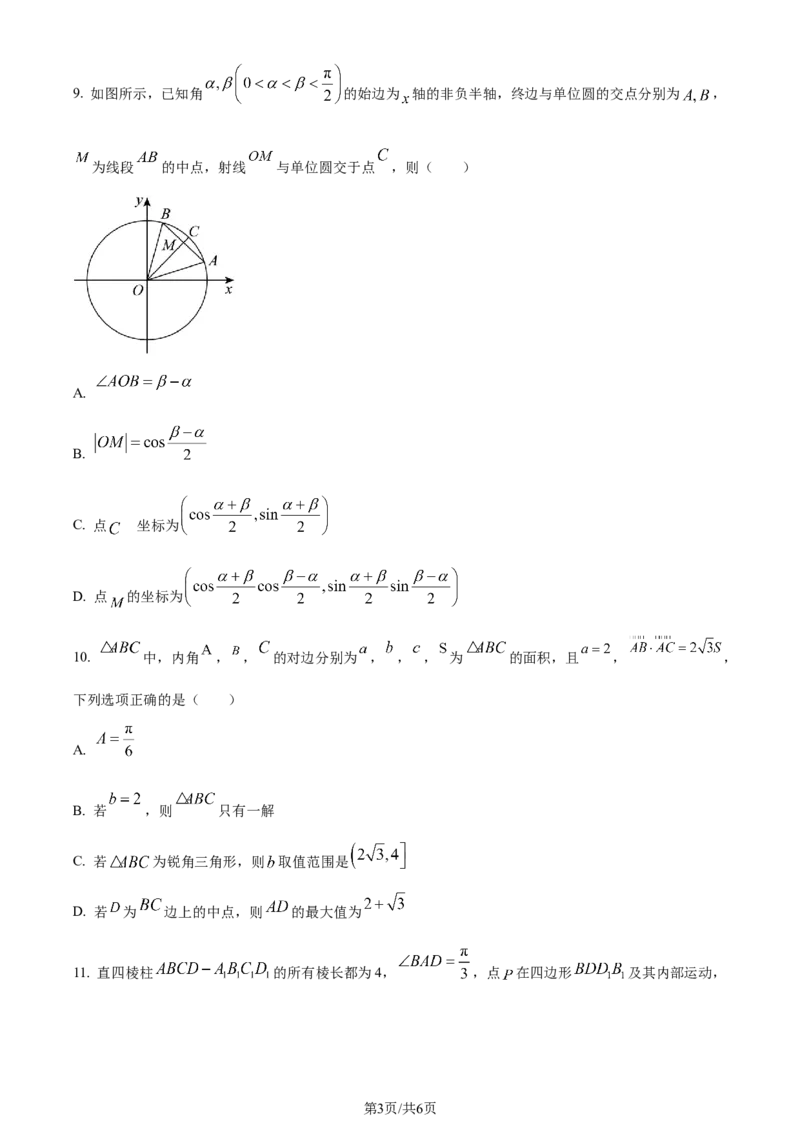
学科网(北京)股份有限公司9. 如图所示,已知角 的始边为 轴的非负半轴,终边与单位圆的交点分别为 ,
为线段 的中点,射线 与单位圆交于点 ,则( )
A.
B.
C. 点 的坐标为
D. 点 的坐标为
10. 中,内角 , , 的对边分别为 , , , 为 的面积,且 , ,
下列选项正确的是( )
A.
B. 若 ,则 只有一解
C. 若 为锐角三角形,则 取值范围是
D. 若 为 边上的中点,则 的最大值为
11. 直四棱柱 的所有棱长都为4, ,点 在四边形 及其内部运动,
第3页/共6页
学科网(北京)股份有限公司且满足 ,则下列选项正确的是( )
A. 点 的轨迹的长度为 .
B. 直线 与平面 所成的角为定值.
C. 点 到平面 的距离的最小值为 .
D. 的最小值为-2.
第Ⅱ卷非选择题
三、填空题:本题共3小题,每小题5分,共15分.
12. 的展开式中 的系数为______.
13. 已知抛物线 的焦点为 , 是 上的动点,过点 作直线 的垂线,垂足为
,则 的最小值为______.
14. 已知函数 , 的定义域为 , 为 的导函数,且 ,
,若 为偶函数,求 =______.
四、解答题:本题共6小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15. 设 为数列 前 项和,已知 是首项为 、公差为 的等差数列.
的
(1)求 的通项公式;
第4页/共6页
学科网(北京)股份有限公司(2)令 , 为数列 的前 项积,证明: .
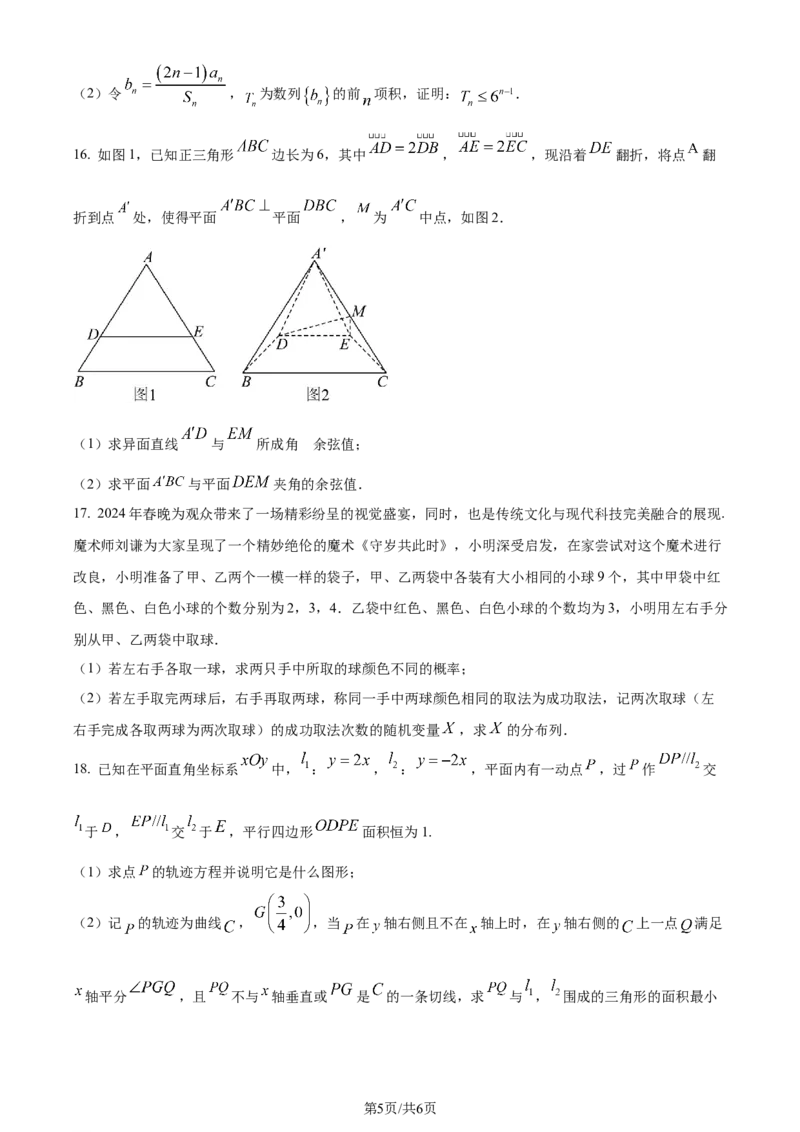
16. 如图1,已知正三角形 边长为6,其中 , ,现沿着 翻折,将点 翻
折到点 处,使得平面 平面 , 为 中点,如图2.
的
(1)求异面直线 与 所成角 余弦值;
(2)求平面 与平面 夹角的余弦值.
17. 2024年春晚为观众带来了一场精彩纷呈的视觉盛宴,同时,也是传统文化与现代科技完美融合的展现.
魔术师刘谦为大家呈现了一个精妙绝伦的魔术《守岁共此时》,小明深受启发,在家尝试对这个魔术进行
改良,小明准备了甲、乙两个一模一样的袋子,甲、乙两袋中各装有大小相同的小球9个,其中甲袋中红
色、黑色、白色小球的个数分别为2,3,4.乙袋中红色、黑色、白色小球的个数均为3,小明用左右手分
别从甲、乙两袋中取球.
(1)若左右手各取一球,求两只手中所取的球颜色不同的概率;
(2)若左手取完两球后,右手再取两球,称同一手中两球颜色相同的取法为成功取法,记两次取球(左
右手完成各取两球为两次取球)的成功取法次数的随机变量 ,求 的分布列.
18. 已知在平面直角坐标系 中, : , : ,平面内有一动点 ,过 作 交
于 , 交 于 ,平行四边形 面积恒为1.
(1)求点 的轨迹方程并说明它是什么图形;
(2)记 的轨迹为曲线 , ,当 在 轴右侧且不在 轴上时,在 轴右侧的 上一点 满足
轴平分 ,且 不与 轴垂直或 是 的一条切线,求 与 , 围成的三角形的面积最小
第5页/共6页
学科网(北京)股份有限公司值.
19. 设A是由 个实数组成的m行n列的数表,如果某一行(或某一列)各数之和为负数,则改变该
行(或该列)中所有数的符号,称为一次“操作”.
(1)数表A如表1所示,若经过两次“操作”,使得到的数表每行的各数之和与每列的各数之和均为非负实
数,请写出每次“操作”后所得的数表(写出一种方法即可):
1 2 3
1 0 1
表1
(2)数表A如表2所示,若必须经过两次“操作”,才可使得到的数表每行的各数之和与每列的各数之和均
为非负整数,求整数a的所有可能值:
a
表2
(3)对由 个实数组成的m行n列的任意一个数表A,能否经过有限次“操作”以后,使得到的数表每
行的各数之和与每列的各数之和均为非负实数?请说明理由.
第6页/共6页
学科网(北京)股份有限公司