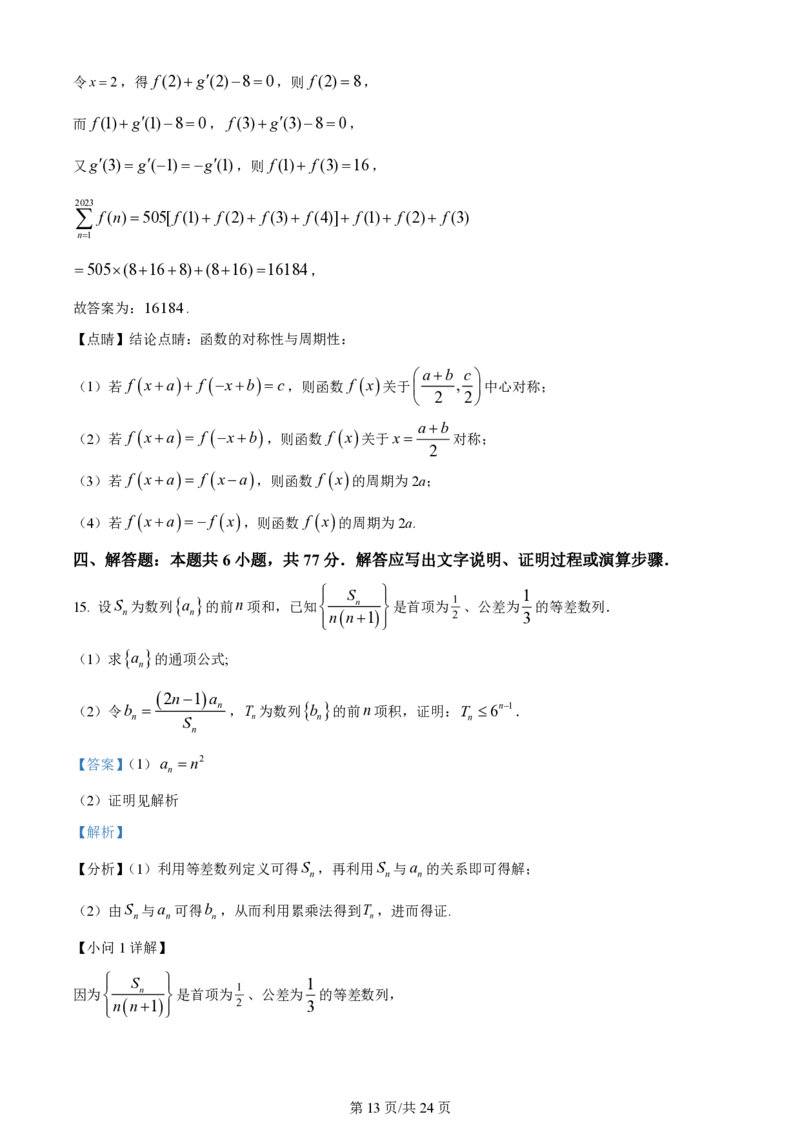精品解析：江西省鹰潭市2024届高三第一次模拟考试数学试题（解析版）_2024年3月_013月合集_2024届江西省鹰潭市高三下学期第一次模拟考试

鹰潭市 2024 届高三第一次模拟考试 数学试卷 本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共 4页．时间 120分钟．满分 150分． 第Ⅰ卷选择题 单项选择题：本题共 8小题，每小题 5分，共 40分．在每小题给出的四个选项中，只有一 项是符合题目要求的，请将正确答案的序号填涂在答题卡上． z1i 1 3i 1. 若复数z满足 ，则z （ ） A. 1i B. 1i C. 22i D. 22i 【答案】B 【解析】 【分析】利用复数的模公式及复数除法法则即可得解.  2 【详解】因为1 3i  12  3 2， 2 21i 所以由z(1i) 1 3i ，得z   1i. 1i 1i1i 故选：B. 2. 已知集合A  x| x2 5x 6  ，集合Bx|xa ，若B ð A ，则a的取值范围为（ ） R A. 6, B. 6, C. ,1 D. ,1 【答案】A 【解析】 【分析】解一元二次不等式求出集合A及ð A，根据集合的包含关系求出结果. R 【详解】因为A  x|x2 5x6    x|x2 5x60  x|1 x6 ， ð A{x x1或x6}， R 因为集合Bx|xa ，B ð A ，所以a 6， R 故选：A. 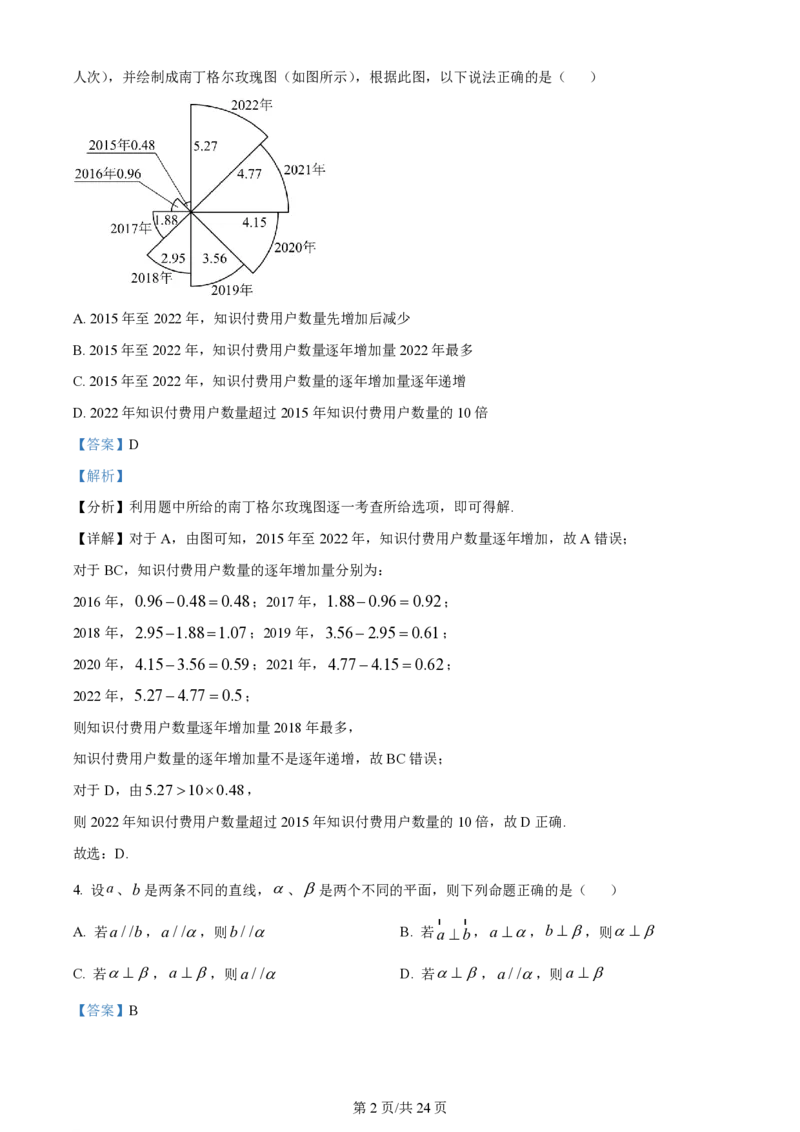3. 南丁格尔玫瑰图是由近代护理学和护士教育创始人南丁格尔（Florence Nightingale）设计的，图中每个 扇形圆心角都是相等的，半径长短表示数量大小．某机构统计了近几年中国知识付费用户数量（单位：亿 第1页/共24页 学科网（北京）股份有限公司人次），并绘制成南丁格尔玫瑰图（如图所示），根据此图，以下说法正确的是（ ） A. 2015年至2022年，知识付费用户数量先增加后减少 B. 2015年至2022年，知识付费用户数量逐年增加量2022年最多 C. 2015年至2022年，知识付费用户数量的逐年增加量逐年递增 D. 2022年知识付费用户数量超过2015年知识付费用户数量的10倍 【答案】D 【解析】 【分析】利用题中所给的南丁格尔玫瑰图逐一考查所给选项，即可得解. 【详解】对于A，由图可知，2015年至2022年，知识付费用户数量逐年增加，故A错误； 对于BC，知识付费用户数量的逐年增加量分别为： 2016年，0.960.480.48；2017年，1.880.960.92； 2018年，2.951.881.07；2019年，3.562.950.61； 2020年，4.153.560.59；2021年，4.774.150.62； 2022年，5.274.770.5； 则知识付费用户数量逐年增加量2018年最多， 知识付费用户数量的逐年增加量不是逐年递增，故BC错误； 对于D，由5.27100.48， 则2022年知识付费用户数量超过2015年知识付费用户数量的10倍，故D正确. 故选：D. 4. 设a、b是两条不同的直线，、是两个不同的平面，则下列命题正确的是（ ） r r A. 若a//b，a//，则b// B. 若ab，a ，b，则 C. 若，a ，则a// D. 若，a//，则a  【答案】B 第2页/共24页 学科网（北京）股份有限公司【解析】 【分析】利用空间直线与平面，平面与平面的位置关系判断ACD，利用空间向量判断线面位置关系，从而 判断B，由此得解. 【详解】对于A，若a//b，a//，则有可能b，故A错误； r r 对于B，若a ，b，则直线a,b的方向向量a,b分别为平面,法向量， r r r r 又ab，即a b，所以，故B正确； 对于C，若，a，则有可能a，故C错误； 对于D，若，a//，则有可能a，故D错误. 故选：B. 5. 某单位为了解职工体重情况，采用分层随机抽样的方法从800名职工中抽取了一个容量为80的样 本．其中，男性平均体重为64千克，方差为151；女性平均体重为56千克，方差为159，男女人数之比 为5:3，则单位职工体重的方差为（ ） A. 166 B. 167 C. 168 D. 169 【答案】D 【解析】 【分析】利用分层抽样的平均数和方差公式即可得解. 5 3 【详解】依题意，单位职工平均体重为x 64 5661， 8 8 5 3 则单位职工体重的方差为s2  15164612 15956612169. 8  8  故选：D.  π cos  cos2    π  π 2  2 6. 已知  0, ，tan      tan， =（ ）  2  4 3  π 2sin     4 1 3 3 A.  B. - C. 3 D. 2 5 5 【答案】D 【解析】 【分析】利用正切的和差公式化简求得tan3，再利用三角函数诱导公式与三角恒等变换，结合正余弦 的齐次式法即可得解. 第3页/共24页 学科网（北京）股份有限公司 π 2 tan1 2 【详解】因为tan     tan，所以  tan，  4 3 1tan 3  π 又  0, ，即tan0，解得tan3，  2  π cos    cos2 sin  cos2sin2   2 所以  sincossin  π sincos 2sin     4 sincossin2 tantan2 332 3     . sin2cos2 tan21 32 1 5 故选：D. 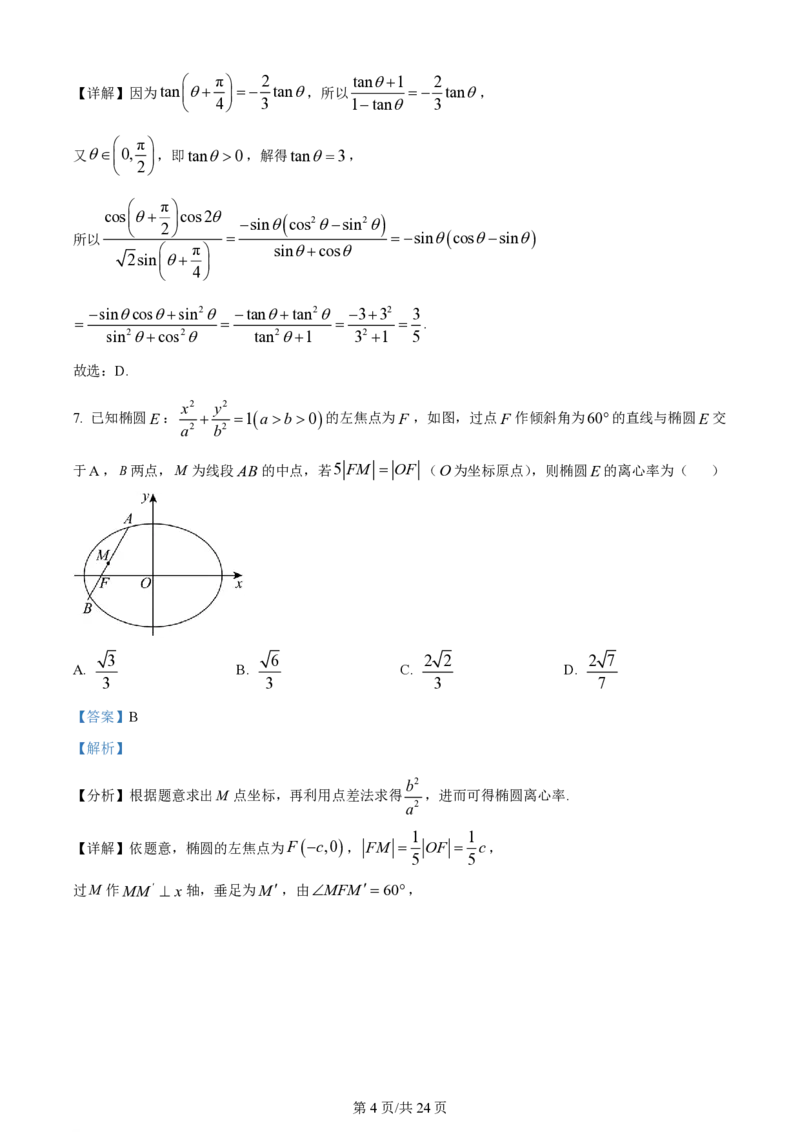x2 y2 7. 已知椭圆E：  1a b0的左焦点为F ，如图，过点F 作倾斜角为60的直线与椭圆E交 a2 b2 于A，B两点，M 为线段AB的中点，若5 FM  OF （O为坐标原点），则椭圆E的离心率为（ ） 3 6 2 2 2 7 A. B. C. D. 3 3 3 7 【答案】B 【解析】 b2 【分析】根据题意求出M 点坐标，再利用点差法求得 ，进而可得椭圆离心率. 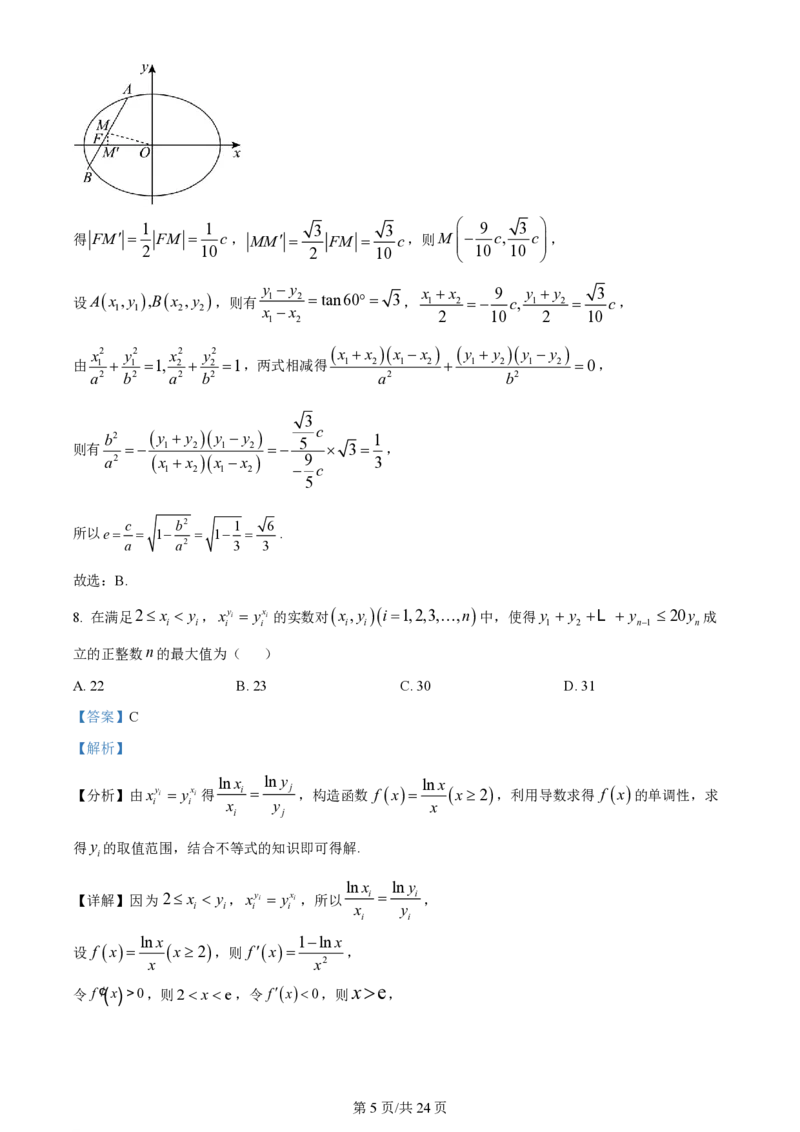a2 1 1 【详解】依题意，椭圆的左焦点为Fc,0 ， FM  OF  c， 5 5 过M 作MM  x轴，垂足为M，由MFM60， 第4页/共24页 学科网（北京）股份有限公司1 1 3 3  9 3  得 FM  FM  c， MM  FM  c，则M  c, c，   2 10 2 10  10 10  y  y x x 9 y  y 3 设Ax ,y ,Bx ,y  ，则有 1 2 tan60 3， 1 2  c, 1 2  c， 1 1 2 2 x x 2 10 2 10 1 2 x2 y2 x2 y2 x x x x  y  y y  y  由 1  1 1, 2  2 1，两式相减得 1 2 1 2  1 2 1 2 0， a2 b2 a2 b2 a2 b2 3 c 则有 b2  y 1  y 2 y 1  y 2   5  3  1 ， a2 x x x x  9 3 1 2 1 2  c 5 c b2 1 6 所以e  1  1  . a a2 3 3 故选：B. 8. 在满足2 x  y ，xy i  yx i 的实数对 x ,y i 1,2,3,,n 中，使得y  y L  y  20y 成 i i i i i i 1 2 n1 n 立的正整数n的最大值为（ ） A. 22 B. 23 C. 30 D. 31 【答案】C 【解析】 lnx ln y lnx 【分析】由xy i  yx i 得 i  j ，构造函数 f x x2，利用导数求得 f x 的单调性，求 i i x y x i j 得y 的取值范围，结合不等式的知识即可得解. i lnx ln y 【详解】因为 2 x  y ，xy i  yx i ，所以 i  i ， i i i i x y i i lnx 1lnx 设 f x x2，则 fx ， x x2 令 f¢(x)>0，则2 xe，令 fx0，则 xe ， 第5页/共24页 学科网（北京）股份有限公司所以 f x 在 2,e 上单调递增，在 e, 上单调递减， ln2 因为 f 2 f 4 ，2 x  y ， f x  f y  ， 2 i i i i 所以2 x e y 4， i i 所以y  y L  y en1 ，又y 4，20y 80， 1 2 n1 n n 80 要使得y  y L  y  20y 成立，只需en180，即n1 30.4， 1 2 n1 n e 所以正整数n的最大值为30. 故选：C. lnx ln y 【点睛】关键点点睛：本题解题的关键是由xy i  yx i 变换得 i  i ，从而得以构造函数 i i x y i i lnx f x x2，由此得解. x 二、多项选择题：本题共 3小题，每小题 6分，共 18分．在每小题给出的四个选项中，有 多项符合题目的要求．全部选对的得 6分，部分选对的得部分分，有选错的得 0分. 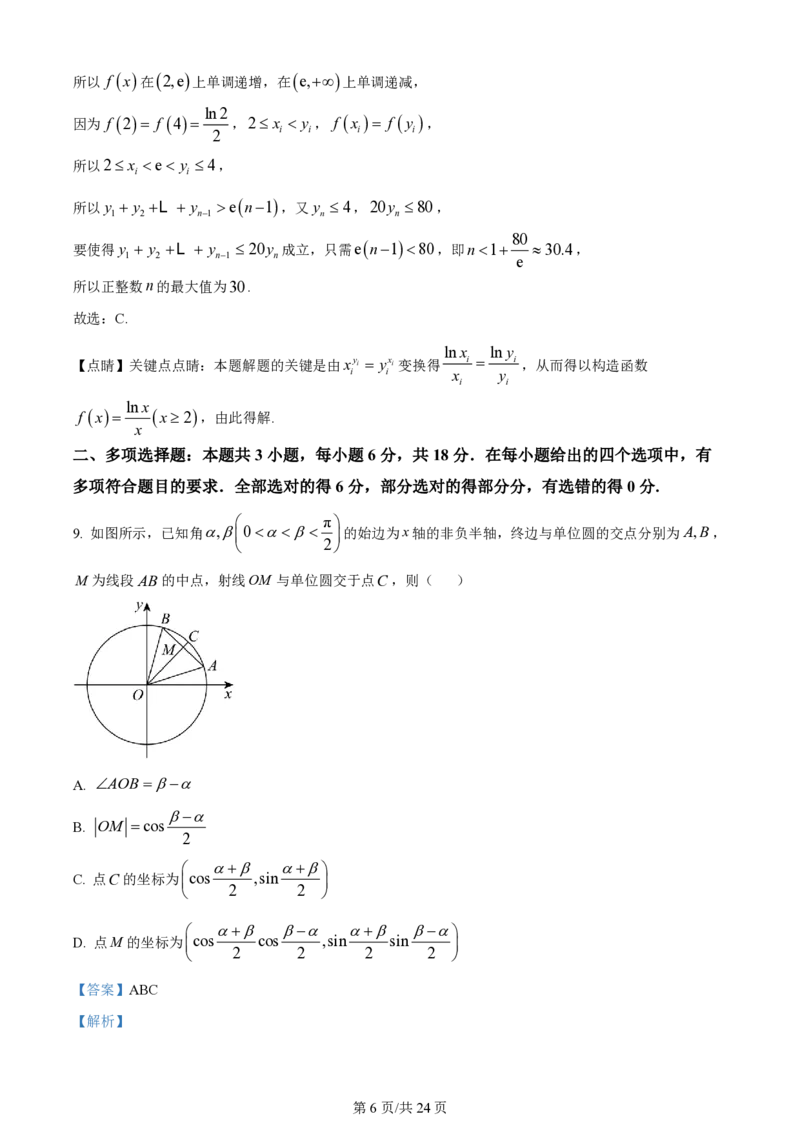 π 9. 如图所示，已知角,  0 的始边为x轴的非负半轴，终边与单位圆的交点分别为A,B，  2 M 为线段AB的中点，射线OM 与单位圆交于点C，则（ ） A. AOB  B. OM cos 2    C. 点C的坐标为 cos ,sin   2 2       D. 点M 的坐标为 cos cos ,sin sin   2 2 2 2  【答案】ABC 【解析】 第6页/共24页 学科网（北京）股份有限公司【分析】由角的定义求解可判断A；由圆的性质及角的定义求解可判断B；由三角函数定义求解可判断 C；由中点坐标公式及三角函数定义，结合角的变换、两角和与差的余弦公式求解可判断D. π 【详解】对于A：因为AOx ,BOx ，0 ，所以AOB，正确； 2  对于B：依题意M 为线段AB的中点，则OM  AB，则AOM  ， 2  又 OA 1，所以 OM  OA cosAOM cos ，正确； 2 对于C：M 为线段AB的中点，射线OM 与单位圆交于点C，则C为» AB的中点，   所以COx  ， 2 2    又 OC 1，所以点C的坐标为 cos ,sin ，正确；  2 2  1 1 1     对于D：x  x x  (coscos)  cos    cos    M 2 A B 2 2  2 2   2 2  1          cos cos sin sin cos cos sin sin   2 2 2 2 2 2 2 2 2  1      2cos cos cos cos ， 2 2 2 2 2 1 1 1     y  y  y  (sinsin) sin  sin       M 2 A B 2 2  2 2   2 2  1          sin cos cos sin sin cos cos sin   2 2 2 2 2 2 2 2 2  1      2sin cos sin cos ， 2 2 2 2 2      所以点M 的坐标为 cos cos ,sin cos ，错误.  2 2 2 2  故选：ABC 10. VABC中，内角A，B，C的对边分别为a，b，c，S为VABC的面积，且a2， uuur uuur ABAC 2 3S，下列选项正确的是（ ） π A. A 6 B. 若b2，则VABC只有一解  C. 若VABC为锐角三角形，则b取值范围是 2 3,4  第7页/共24页 学科网（北京）股份有限公司D. 若D为BC边上的中点，则AD的最大值为2 3 【答案】ABD 【解析】 【分析】利用平面向量数量积公式及三角形面积公式可判定A，直接解三角形可判定B，利用角的范围结合 正弦定理可判定C，利用平面向量中线的性质及数量积公式结合余弦定理、基本不等式可判定D. uuur uuur 1 3 【详解】对于A，因为ABAC 2 3S，所以bccosA2 3 bcsin A，则tanA ， 2 3 π 因为A0,π ，所以A ，故A正确； 6 π 2π 对于B，因为b2a，则B A ，C  ，故VABC只有一解，故B正确； 6 3  π  π 对于C，若VABC为锐角三角形，则B  0, ，C  0, ，  2  2  π 0 B   2 π π  3  则 ，则  B ，即sinB ,1，   π π 3 2 2    0π B  6 2 asinB   由正弦定理可知：b 4sinB 2 3,4 ，故C错误； sin A uuur 1 uuur uuur  对于D，若D为BC边上的中点，则AD ABAC ， 2 uuur 2 1uuur 2 uuur uuur uuur 2  1  所以AD  AB 2ABAC AC  b2 c2  3bc 4 4 由余弦定理知a2 b2 c2 2bccosAb2 c2  3bc4，得b2 c2  3bc4， 4 又b2 c2  3bc42bc，所以bc 4 38， 2 3 当且仅当bc 2 6 时取得等号， uuur 所以AD 2  1 b2 c2  3bc   1 42 3bc   1 42 3  4 38  74 3， 4 4 4  即 AD  74 3 2 3，故D正确. 故选：ABD. π 11. 直四棱柱ABCDABC D 的所有棱长都为4，BAD ，点P在四边形BDDB 及其内部运动， 1 1 1 1 3 1 1 且满足 PA  PC 8，则下列选项正确的是（ ） 第8页/共24页 学科网（北京）股份有限公司A. 点P的轨迹的长度为π. B. 直线AP与平面BDDB 所成的角为定值． 1 1 2 21 C. 点P到平面ADB 的距离的最小值为 . 1 1 7 uuur uuuur D. PA PC 的最小值为-2． 1 1 【答案】BC 【解析】 【分析】建立空间直角坐标系，表示 PA  PC 8，化简后得点P的轨迹方程，得轨迹长度判断A；向量 法求线面角判断B，向量法求点到平面距离，结合点P的轨迹得最小值判断C；坐标表示向量数量积，结合 点P的轨迹最小值判断D. 【详解】直四棱柱ABCDABC D 的所有棱长都为4，则底面ABCD为菱形， 1 1 1 1 π 又BAD ，则△ABD和△CBD都是等边三角形， 3 设BD与AC相交于点O，由BD AC，以O为原点，OA为x轴，OB为y轴，过O垂直于底面的直 线为z轴，建立如图所示的空间直角坐标系，     则有A 2 3,0,0 ,B0,2,0,C 2 3,0,0 ,D0,2,0 ，     A 2 3,0,4 ,B 0,2,4,C 2 3,0,4 ,D 0,2,4 ， 1 1 1 1 点P在四边形BDDB 及其内部运动，设P0,y,z ，2 y2,0 z 4， 1 1 第9页/共24页 学科网（北京）股份有限公司 2  2 由 PA  PC 8，有 2 3  y2 z2  2 3  y2 z2 8， 即y2 z2 42 y2,0 z 2 ， 所以点P的轨迹为 yOz平面内，以O为圆心，2为半径的半圆弧， 所以点P的轨迹的长度为2π， A选项错误； uuur r   平面BDDB 的法向量为m1,0,0 ，AP 2 3,y,z ， 1 1 uuur r APm 2 3 3 直线AP与平面BDDB 所成的角为，则sin uuur r   ， 1 1 AP m 12 y2 z2 2  π π 又由 0, ，则 ，    2 3 所以直线AP与平面BDDB 所成的角为定值， B选项正确； 1 1     r AB = 2 3,2,4 ,AD 2 3,2,4 ，设平面ADB 的一个法向量为n x,y,z ， 1 1 1 1 r  AB n=2 3x2y4z 0 r   则有 1 r ，令x2，得y0,z 3，n  2,0, 3 ，  AD n=2 3x2y4z 0 1 uuur r APn 2 32 3z 4 3 3z 所以点P到平面ADB 的距离 d  r =  ， 1 1 n  2 7 22  3 4 32 3 2 21 0 z2，所以z 2时，d   ， min 7 7 2 21 所以点P到平面ADB 的距离的最小值为 ，C选项正确； 1 1 7 uuur uuuur     PA= 2 3, y,4z ,PC  2 3, y,4z ， 1 1 uuur uuuur PA PC =12 y2 z42 ，其几何意义为点Py,z 到点 0,4 距离的平方减12， 1 1 由y2 z2 4，点Py,z 到点 0,4 距离最小值为422， uuur uuuur PA PC 的最小值为22 128，D选项错误. 1 1 故选：BC . 【点睛】方法点睛： 空间几何体中的相关问题，要利用好几何体本身的结构特征，点线面的位置关系，图形中的角度和距离 第10页/共24页 学科网（北京）股份有限公司等，建立空间直角坐标系，利用向量法解决问题，也是常用的方法. 第Ⅱ卷非选择题 三、填空题：本题共 3小题，每小题 5分，共 15 分． 2x y6 y 12. 的展开式中 的系数为______． x2y4 x 【答案】12 【解析】 2x y6 【分析】由题意得 的展开式通项，令r41，求出r回代到通项公式中去即可求解. x2y4 2x y6 【详解】 的展开式通项为 x2y4 T Cr 2x6ryr r1  6 Cr26r1r x4ryr4,  0r 6,rN* ， x2y4 x2y4 6 由题意令r41，解得r =5， 2x y6 y 所以 的展开式中 的系数为C526515 6212. x2y4 x 6 故答案为：12. 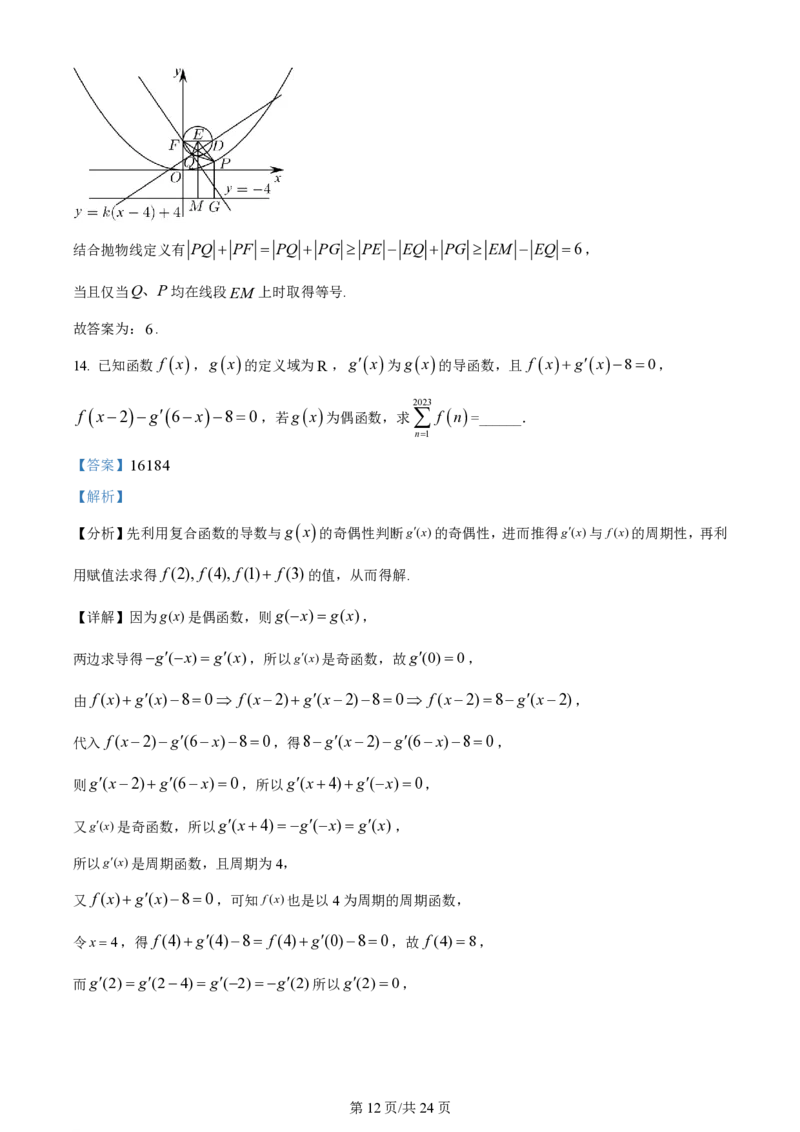13. 已知抛物线x2 16y的焦点为F ，P是C上的动点，过点F 作直线y kx44的垂线，垂足为 Q，则 PQ  PF 的最小值为______． 【答案】6 【解析】 【分析】先分析得Q的轨迹，再利用抛物线的定义，结合圆的性质数形结合即可得解. 【详解】如图所示，易知F0,4 ，直线y kx44过定点D4,4 ， 因为FQQD，所以Q在以FD为直径的圆上， 不妨设其圆心为E2,4 ，显然半径 EQ 2， 分别过E,P 作准线 y  4的垂线EM,PG，垂足为M,G， EM 8 第11页/共24页 学科网（北京）股份有限公司结合抛物线定义有 PQ  PF  PQ  PG  PE  EQ  PG  EM  EQ 6， 当且仅当Q、P均在线段EM 上时取得等号. 故答案为：6. 14. 已知函数 f x ，gx 的定义域为R ，gx 为gx 的导函数，且 f xgx80， 2023 f x2g6x80，若gx 为偶函数，求  f n =______． n1 【答案】16184 【解析】 【分析】先利用复合函数的导数与gx 的奇偶性判断g(x)的奇偶性，进而推得g(x)与 f(x)的周期性，再利 用赋值法求得 f(2), f(4), f(1) f(3)的值，从而得解. 【详解】因为g(x)是偶函数，则g(x) g(x)， 两边求导得g(x) g(x)，所以g(x)是奇函数，故g(0)0， 由 f(x)g(x)80 f(x2)g(x2)80 f(x2)8g(x2)， 代入 f(x2)g(6x)80，得8g(x2)g(6x)80， 则g(x2)g(6x)0，所以g(x4)g(x)0， 又g(x)是奇函数，所以g(x4)g(x) g(x)， 所以g(x)是周期函数，且周期为4， 又 f(x)g(x)80，可知 f(x)也是以4为周期的周期函数， 令x4，得 f(4)g(4)8 f(4)g(0)80，故 f(4)8， 而g(2) g(24) g(2)g(2)所以g(2)0， 第12页/共24页 学科网（北京）股份有限公司令x2，得 f(2)g(2)80，则 f(2)8， 而 f(1)g(1)80， f(3)g(3)80， 又g(3) g(1)g(1)，则 f(1) f(3)16， 2023  f(n)505[f(1) f(2) f(3) f(4)] f(1) f(2) f(3) n1 505(8168)(816)16184， 故答案为：16184. 【点睛】结论点睛：函数的对称性与周期性： ab c （1）若 f xa f xbc，则函数 f x 关于 , 中心对称；  2 2 ab （2）若 f xa f xb ，则函数 f x 关于x 对称； 2 （3）若 f xa f xa ，则函数 f x 的周期为2a； （4）若 f xaf x ，则函数 f x 的周期为2a. 四、解答题：本题共 6小题，共 77分．解答应写出文字说明、证明过程或演算步骤．  S  1 15. 设S 为数列 a  的前n项和，已知 n 是首项为 1 、公差为 的等差数列． n n  nn1  2 3 （1）求 a  的通项公式; n 2n1a （2）令b  n ，T 为数列 b  的前n项积，证明：T 6n1． n S n n n n 【答案】（1）a n2 n （2）证明见解析 【解析】 【分析】（1）利用等差数列定义可得S ，再利用S 与a 的关系即可得解； n n n （2）由S 与a 可得b ，从而利用累乘法得到T ，进而得证. n n n n 【小问1详解】  S  1 因为 n 是首项为 1 、公差为 的等差数列，  nn1  2 3 第13页/共24页 学科网（北京）股份有限公司S 1 1 n 1 故 n   n1  ， nn1 2 3 3 6 n 1 n2n1n1 即S     nn1 ， n 3 6 6 n2n1n1 当n2时，S  ， n1 6 n2n1n1 n2n1n1 故S S a   n n1 n 6 6 n  2n2 3n12n2 3n1   n2， 6 32 当n1时，a S  1，符合上式， 1 1 6 故a n2； n 【小问2详解】 n2n1n1 由a n2，S  ， n n 6 2n1a 62n1n2 62n1n 故b  n   ， n S n2n1n1 2n1n1 n 611 632 653 62n1n 6n 则T bb L b    L  ， n 1 2 n 32 53 74 2n1n1 2n1n1 因为 2n1n1326，故T  6n 6n1. 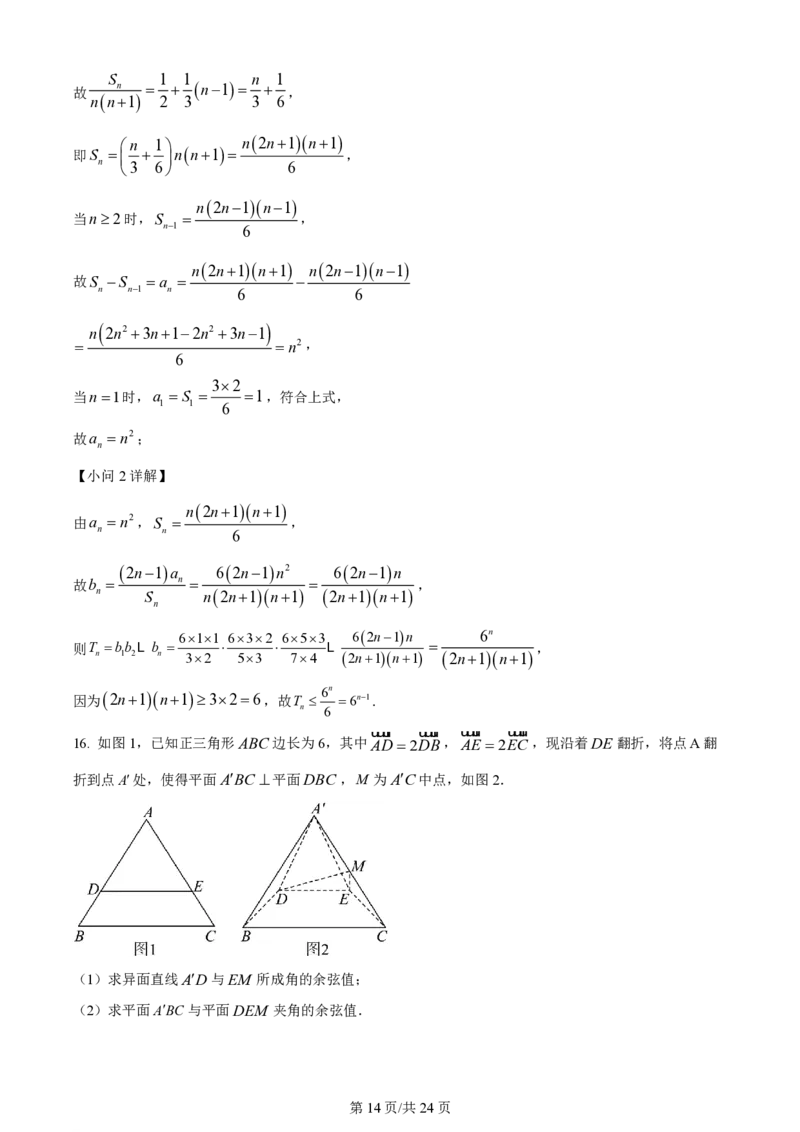n 6 uuur uuur uuur uuur 16. 如图1，已知正三角形ABC边长为6，其中AD2DB，AE 2EC ，现沿着DE翻折，将点A翻 折到点A处，使得平面ABC 平面DBC，M 为AC中点，如图2． （1）求异面直线AD与EM 所成角的余弦值； （2）求平面ABC与平面DEM 夹角的余弦值． 第14页/共24页 学科网（北京）股份有限公司13 22 【答案】（1） 88 21 （2） 7 【解析】 【分析】（1）设O为BC的中点，结合图形翻折的性质推出AO 平面DBC，从而建立空间直角坐标 系，求得相关线段长与相关点坐标，利用空间角的向量求法即可得解； （2）分别求出平面ABC与平面DEM 的法向量，根据空间角的向量法即可得解. 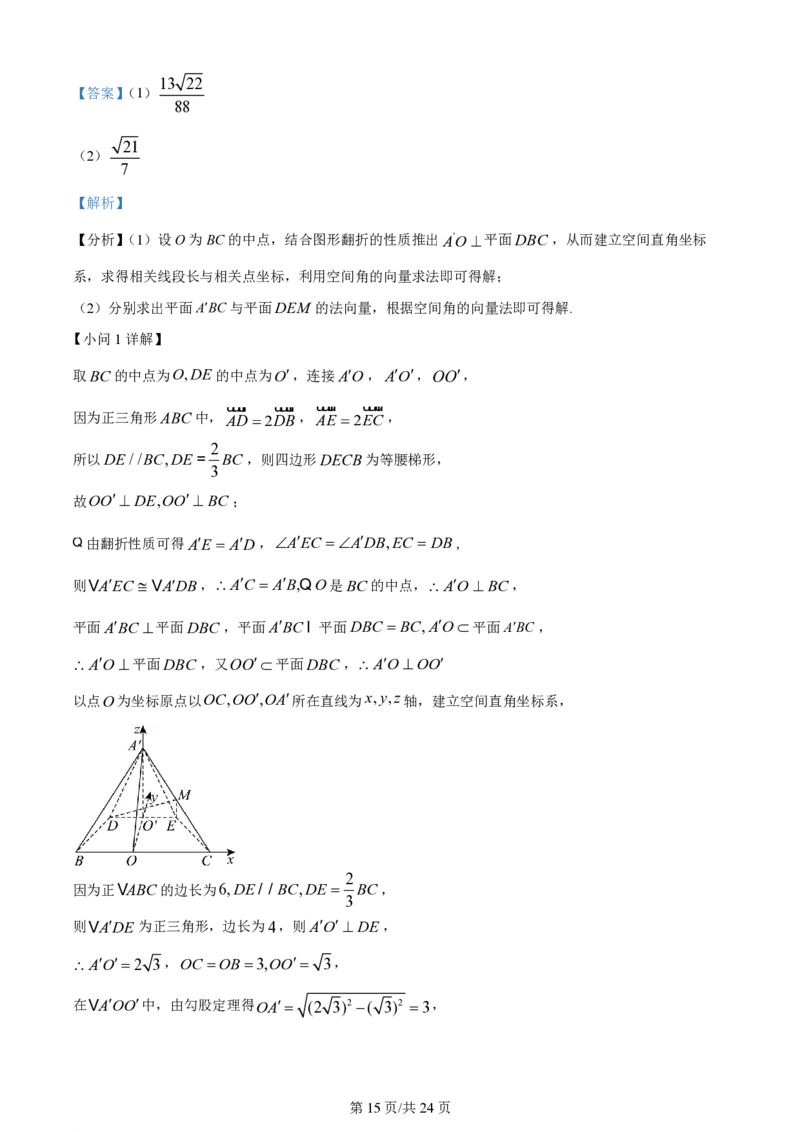【小问1详解】 取BC的中点为O,DE的中点为O，连接AO，AO，OO， uuur uuur uuur uuur 因为正三角形ABC中，AD2DB，AE 2EC ， 2 所以DE//BC,DE = BC，则四边形DECB为等腰梯形， 3 故OO DE,OO BC； Q由翻折性质可得AE  AD，AEC ADB,EC  DB, 则VAEC  VADB，AC  AB,QO是BC的中点，AO BC， 平面ABC 平面DBC，平面ABCI 平面DBC  BC,AO平面ABC， AO平面DBC，又OO平面DBC，AOOO 以点O为坐标原点以OC,OO,OA所在直线为x,y,z轴，建立空间直角坐标系， 2 因为正VABC的边长为6,DE/ / BC,DE  BC， 3 则VADE 为正三角形，边长为4，则AO DE ， AO2 3，OC OB3,OO 3， 在VAOO中，由勾股定理得OA (2 3)2 ( 3)2 3， 第15页/共24页 学科网（北京）股份有限公司    3 3 A0,0,3,D 2, 3,0 ,E 2, 3,0 ,C(3,0,0),M  ,0, ， 2 2 uuuur uuuur    1 3 则AD 2, 3,3 ,EM    , 3, ，  2 2 uuuur uuuur 9 uuuur uuuur ADEM 13 13 22 2 cosAD,EM  uuuur uuuur   ， AD  EM 1 9 88 4 3 4 4  π Q异面直线所成角的取值范围为 0,  ，  2 13 22 异面直线AD与EM 所成角的余弦值为 . 88 【小问2详解】     3 3 由（1）得D 2, 3,0 ，E 2, 3,0 ,M  ,0, ， 2 2 uuur uuuur 7 3 DE 4,0,0,DM   , 3, ， 2 2 r 易得平面ABC的一个法向量为m 0,1,0， r 设平面DEM 的法向量为n x,y,z ， uuur r 4x0  DEn 0  r   则uuuur r ，即7 3 ，令z 2，则n  0, 3,2 ， DM n 0  x 3y z 0 2 2 r r r r mn 3 21 cosm,n  r r   ， m  n 1 34 7 21 平面ABC与平面DEM 夹角的余弦值为 . 7 17. 2024年春晚为观众带来了一场精彩纷呈的视觉盛宴，同时，也是传统文化与现代科技完美融合的展现. 魔术师刘谦为大家呈现了一个精妙绝伦的魔术《守岁共此时》，小明深受启发，在家尝试对这个魔术进行 改良，小明准备了甲、乙两个一模一样的袋子，甲、乙两袋中各装有大小相同的小球9个，其中甲袋中红 色、黑色、白色小球的个数分别为2，3，4．乙袋中红色、黑色、白色小球的个数均为3，小明用左右手 分别从甲、乙两袋中取球． 第16页/共24页 学科网（北京）股份有限公司（1）若左右手各取一球，求两只手中所取的球颜色不同的概率； （2）若左手取完两球后，右手再取两球，称同一手中两球颜色相同的取法为成功取法，记两次取球（左 右手完成各取两球为两次取球）的成功取法次数的随机变量X ，求X 的分布列． 2 【答案】（1） 3 （2）分布列见解析 【解析】 【分析】（1）根据给定条件，利用古典概型及对立事件的概率公式即可得解； （2）求出X 的可能取值，再求出各个值对应的概率，求出分布列即可得解. 【小问1详解】 记事件A为“两手所取的球不同色”，事件A是两手所取球颜色相同， 233343 1 2 则P(A)  ，所以P(A)1P(A) . 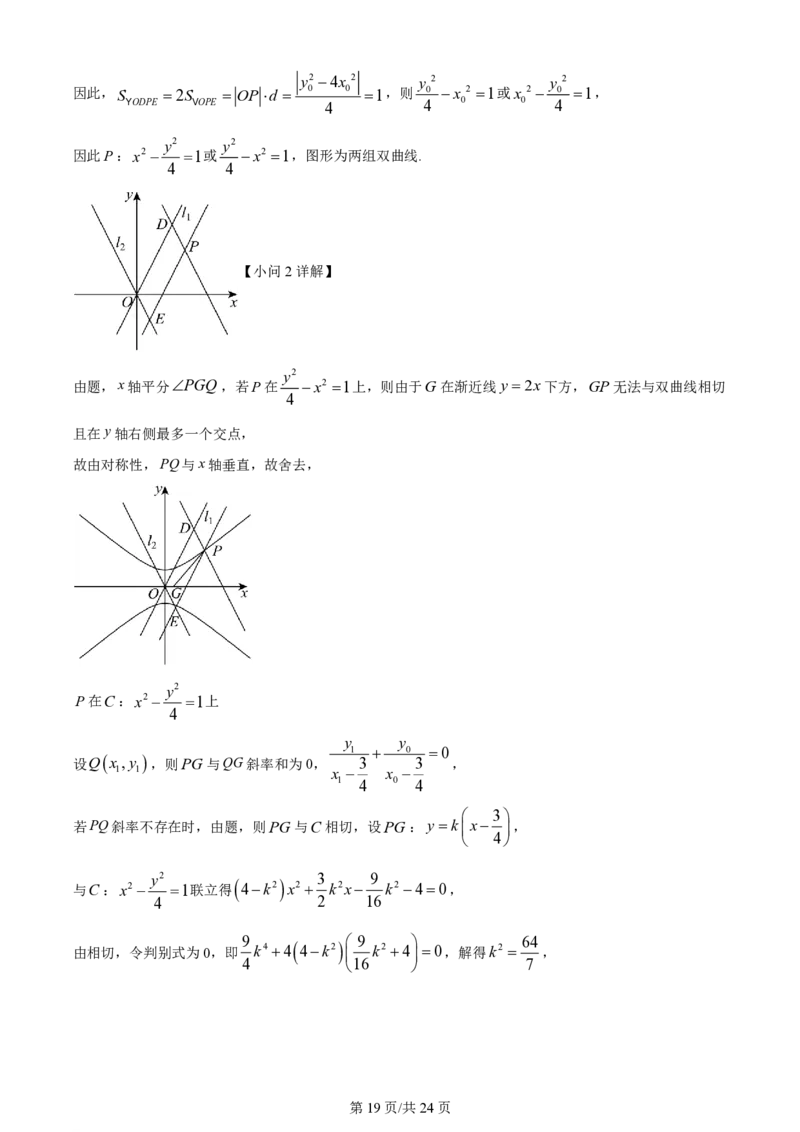99 3 3 【小问2详解】 依题意，X 的可能取值为0,1,2， C2C2C2 5 左手所取的两球颜色相同的概率为 2 3 4  ， C2 18 9 C2C2C2 1 右手所取的两球颜色相同的概率为 3 3 3  ， C2 4 9 5 1 13 3 13 P(X 0)(1 )(1 )   ， 18 4 18 4 24 5 1 5 1 7 P(X 1) (1 )(1 )  ， 18 4 18 4 18 5 1 5 P(X 2)   ， 18 4 72 所以X 的分布列为： X 0 1 2 13 7 5 P 24 18 72 18. 已知在平面直角坐标系xOy中，l ：y 2x，l ：y 2x，平面内有一动点P，过P作DP//l 交 1 2 2 l 于D，EP//l 交l 于E，平行四边形ODPE面积恒为1. 1 1 2 第17页/共24页 学科网（北京）股份有限公司（1）求点P的轨迹方程并说明它是什么图形； 3  （2）记P的轨迹为曲线C，G  ,0 ，当P在y轴右侧且不在x轴上时，在y轴右侧的C上一点Q满足 4  x轴平分PGQ，且PQ不与x轴垂直或PG是C的一条切线，求PQ与l ，l 围成的三角形的面积最小 1 2 值. y2 y2 【答案】（1）x2  1或 x2 1，图形为两组双曲线 4 4 32 （2） 9 【解析】  x 1 y  【分析】（1）联立直线的方程可得点E  0  y , 0 x ，进而根据点到直线的距离公式，结合三角形  2 4 0 2 0  面积公式即可化简得轨迹方程， y2 （2）根据Q满足x轴平分PGQ，确定P在C：x2  1上，即可联立直线直线与双曲线方程，利 4 4 4  用相切可得直线方程为PQ：x ，利用斜率之和可得直线PQ恒过定点 ,0 ，即可设直线方程为 3 3  4 1 1 xmy   m ，联立直线间的方程可得M,N 坐标，即可由面积公式求解. 3 2 2 【小问1详解】 设点Px ,y  0 0 则直线PD的方程为y y 2xx  ， 0 0  x 1 x 0  y y y 2xx    2 4 0  x 1 y  联立 0 0 ，解得 ，即点E  0  y , 0 x ， y 2x  y  y 0 x  2 4 0 2 0   2 0 直线OP的方程为y xx y 0， 0 0  x 1   y  y 0  y x 0 x 点E到直线OP的距离为 0   2 4 0   0   2 0   y 0 2 4x 0 2 d   x2  y2 4 x2  y2 0 0 0 0 且 OP  x2  y2 ， 0 0 第18页/共24页 学科网（北京）股份有限公司y2 4x 2 y 2 y 2 因此，S 2S  OP d  0 0 1，则 0 x 2 1或x 2  0 1， YODPE VOPE 4 4 0 0 4 y2 y2 因此P：x2  1或 x2 1，图形为两组双曲线. 4 4 【小问2详解】 y2 由题，x轴平分PGQ，若P在 x2 1上，则由于G在渐近线y 2x下方，GP无法与双曲线相切 4 且在y轴右侧最多一个交点， 故由对称性，PQ与x轴垂直，故舍去， y2 P在C：x2  1上 4 y y 1  0 0 设Qx ,y  ，则PG与QG斜率和为0， 3 3 ， 1 1 x  x  1 4 0 4  3 若PQ斜率不存在时，由题，则PG与C相切，设PG：y k  x ，  4 与C：x2  y2 1联立得  4k2 x2  3 k2x 9 k2 40， 4 2 16 由相切，令判别式为0，即 9 k4 4  4k2  9 k2 4   0，解得k2  64 ， 4 16  7 第19页/共24页 学科网（北京）股份有限公司3 k2 4 4 此时x  2  ，所以PQ：x ， 0 2  k2 4  3 3 y y 1  0 0 3 PQ斜率存在时，由 3 3 ，得x y x y  y  y ，则 x  x  1 0 0 1 4 0 1 1 4 0 4  y2   y2  x y x y  x 1 2y 0 2 x 0 2y 1 2  4  1 4 1   y 0 2 4  1 4 0   y 1 2  4  y 0 2  y 1 2  4 y  y  ， 1 0 0 1 x y x y 3y  y  3y  y  3 0 1 1 0 0 1 0 1 0 1 y y 0  1 4  整理得 4 4 ，故PQ恒过定点 ,0 ，且其斜率的绝对值大于渐近线的斜率， x  x  3  0 3 1 3 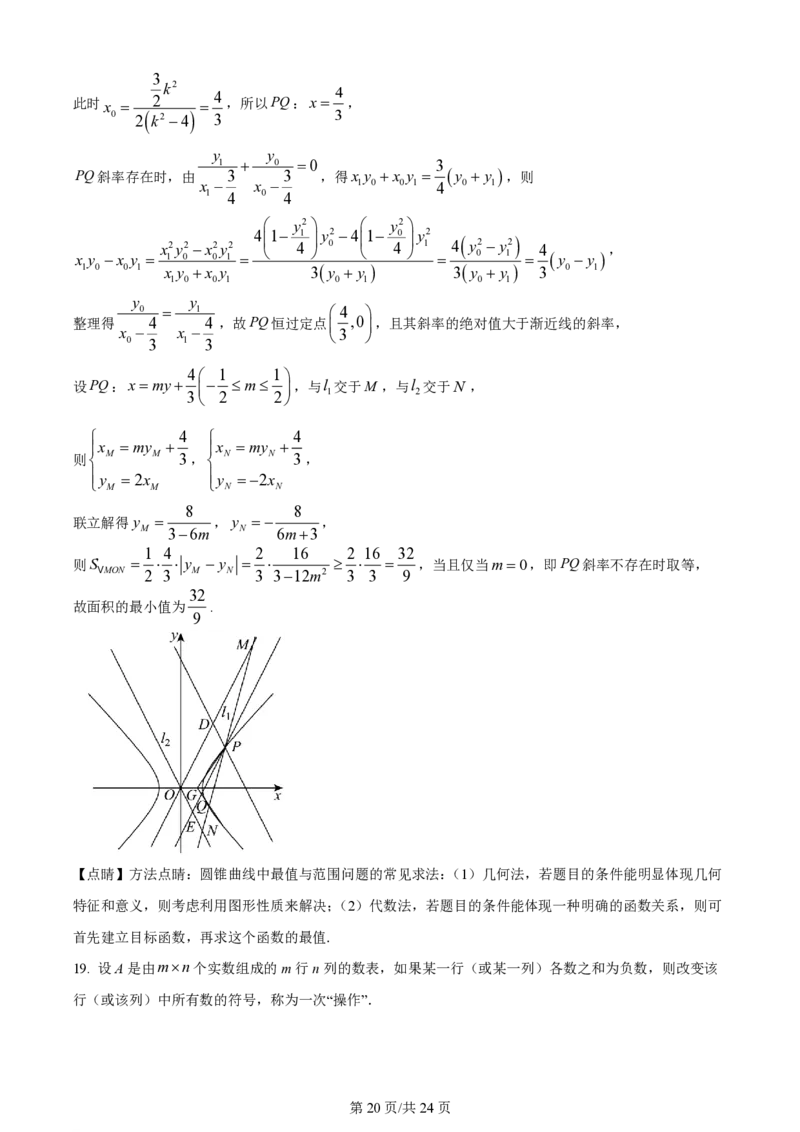4 1 1 设PQ：xmy   m ，与l 交于M ，与l 交于N ， 3 2 2 1 2  4  4 x my  x my  则 M M 3， N N 3 ， y 2x y 2x   M M N N 8 8 联立解得y  ，y  ， M 36m N 6m3 1 4 2 16 2 16 32 则S    y  y      ，当且仅当m0，即PQ斜率不存在时取等， VMON 2 3 M N 3 312m2 3 3 9 32 故面积的最小值为 . 9 【点睛】方法点睛：圆锥曲线中最值与范围问题的常见求法：（1）几何法，若题目的条件能明显体现几何 特征和意义，则考虑利用图形性质来解决；（2）代数法，若题目的条件能体现一种明确的函数关系，则可 首先建立目标函数，再求这个函数的最值. 19. 设A是由mn个实数组成的m行n列的数表，如果某一行（或某一列）各数之和为负数，则改变该 行（或该列）中所有数的符号，称为一次“操作”． 第20页/共24页 学科网（北京）股份有限公司（1）数表A如表1所示，若经过两次“操作”，使得到的数表每行的各数之和与每列的各数之和均为非负 实数，请写出每次“操作”后所得的数表（写出一种方法即可）： 1 2 3 7 2 1 0 1 表1 （2）数表A如表2所示，若必须经过两次“操作”，才可使得到的数表每行的各数之和与每列的各数之和 均为非负整数，求整数a的所有可能值： a a2 1 a a2 2a 1a2 a2 a2 表2 （3）对由mn个实数组成的m行n列的任意一个数表A，能否经过有限次“操作”以后，使得到的数表每 行的各数之和与每列的各数之和均为非负实数？请说明理由． 【答案】（1）答案见解析； （2）a 0或a1 （3）证明见解析. 【解析】 【分析】（1）根据题中一次“操作”的含义，将原数表改变第4列，再改变第2行即可；或者改变第2行，改 变第4列也可得（写出一种即可）； （2） 每一列所有数之和分别为2，0，2，0，每一行所有数之和分别为1，1；①如果先操作第三列，第 一行之和为2a1，第二行之和为52a，再考虑第二次操作，由此列出不等关系解得a；②如果操作第一 行，再根据各列的和考虑第二次操作，由条件列不等式求a，（3） 按要求对某行（或某列）操作一次时， 则该行的行和（或该列的列和），由负整数变为正整数，都会引起该行的行和（或该列的列和）增大，从而 也就使得数阵中mn个数之和增加，由此证明结论． 【小问1详解】 法1： 1 2 3 7 1 2 3 7 1 2 3 7 改变第四列 改变第二行 2 1 0 1 2 1 0 1 2 1 0 1 法2： 第21页/共24页 学科网（北京）股份有限公司1 2 3 7 1 2 3 7 1 2 3 7 改变第二行 改变第四列 2 1 0 1 2 1 0 1 2 1 0 1 法3： 1 2 3 7 1 2 3 7 1 2 3 7 改变第一列 改变第四列 2 1 0 1 2 1 0 1 2 1 0 1 （写出一种即可） 【小问2详解】 数表A a a2 1 a a2 2a 1a2 a2 a2 每一列所有数之和分别为2，0，2，0，每一行所有数之和分别为1，1; ①如果先操作第三列，则 a a2 1 a a2 2a 1a2 2a a2 则第一行之和为2a1，第二行之和为52a， 5 若2a10，则52a0，即a ， 2 再操作第二行，则 a a2 1 a a2 a2 a2 1 a2 a2 此时第四列为负数，不满足要求； 1 若2a10，则52a0，即a ， 2 再操作第一行，则 a 1a2 a a2 第22页/共24页 学科网（北京）股份有限公司2a 1a2 2a a2 由已知，22a0,22a2 0,22a0，又a为整数， 解得a 0或a1， 若a 0，则 0 1 0 0 2 1 2 0 若a1，则 1 0 1 1 3 0 3 1 所以a 0或a1满足要求， ②如果先操作第一行，则 a 1a2 a a2 2a 1a2 a2 a2 则第一列的所有数的和为22a，第二列的所有数的和为22a2， 第三列的所有数的和为2a2，第四列的所有数的和为2a2， 若a 1，则22a 0,2a20,22a2 0,2a2 2，与已知矛盾， 若a 1，则22a0,2a20,22a2 0,2a2 2，与已知矛盾， 若a 1，则22a 0,2a20，又a为整数， 由已知22a2 0，所以a 0或a1， 若a 0，则 0 1 0 0 2 1 2 0 再操作第三列即可， 若a1，则 第23页/共24页 学科网（北京）股份有限公司1 0 1 1 3 0 3 1 再操作第三列即可. 综上，a 0或a1， 【小问3详解】 按要求对某行（或某列）操作一次时，则该行的行和（或该列的列和）由负整数变为正整数，都会引起该 行的行和（或该列的列和）增大，从而也就使得数阵中mn个数之和增加，且增加的幅度大于等于1(1)2， 但是每次操作都只是改变数表中某行（或某列）各数的符号，而不改变其绝对值，显然，数表中mn个数之 m n 和必然小于等于  a ，可见其增加的趋势必在有限次之后终止,终止之时必然所有的行和与所有的列和 ij i1 j1 均为非负整数，故结论成立. 【点睛】关键点点睛：“新定义”主要是指即时定义新概念、新公式、新定理、新法则、新运算五种，然后 根据此新定义去解决问题，有时还需要用类比的方法去理解新的定义，这样有助于对新定义的透彻理解.但 是，透过现象看本质，它们考查的还是基础数学知识，所以说“新题”不一定是“难题”，掌握好三基，以不 变应万变才是制胜法宝. 第24页/共24页 学科网（北京）股份有限公司