文档内容
周南中学 2025 届高三上学期第四阶段考试数学试卷参考答案
1. 已知集合 A={x∈N∗/−20
A. 2 B. 3 C. 4 D. 5
答案: C
6. 在中国古代, 人们用圭表测量日影长度来确定节气, 一年之中日影最长的一天被定为冬至. 从
冬至算起, 依次有冬至、小寒、大寒、立春、雨水、惊蛰、春分、清明、谷雨、立夏、 小满、
芒种这十二个节气, 其日影长依次成等差数列, 若冬至、立春、春分日影长之和为 31.5 尺,小
寒、雨水,清明日影长之和为 28.5 尺,则大寒、惊蛰、谷雨日影长之和为( )
A. 25.5 尺 B. 34.5 尺 C. 37.5 尺 D. 96 尺
【答案】A
【详解】设从冬至日起,小寒、大寒、立春、雨水、惊蛰、春分、清明、谷雨、立夏、小满、
芒种这十二个节气其日影长依次成等差数列 {a } ,如冬至日的日影长为 a 尺,设公差为 d 尺.
n 1
由题可知,所以 a +a +a =31.5⇒3a =31.5⇒a =10.5 ,
1 4 7 4 4
a +a +a =28.5⇒3a =28.5⇒a =9.5 ,d=a −a =9.5−10.5=−1,
2 5 8 5 5 5 4
a +a +a =3a =3(a +d)=3×(9.5−1)=3×8.5=25.5 ,
3 6 9 6 5
故选: A.
( √2) ( √2)
7. 已知 ⃗a= √3sinωx,cosωx− ,⃗b= cosωx,cosωx+ ω>0 ,若函数 f (x)=⃗a⋅⃗b
2 2
在区间 [0,π] 上恰好有 5 个最大值,4 个最小值,则实数 ω 的取值范围是 ( )
[25 14] [25 14) [14 31] [14 31)
A. , B. , C. , D. ,
6 3 6 3 3 6 3 6
【答案】B
【详解】根据题意可得:
f (x)=⃗a⋅⃗b=√3sinωxcosωx+cos2ωx− 1 = √3 sin2ωx+ 1 cos2ωx=sin ( 2ωx+ π)
2 2 2 6
π [π π]
由于 x∈[0,π] ,可得: 2ωx+ ∈ ,2ωπ+ ,
6 6 6
由于函数 f (x) 恰好有 5 个最大值,4 个最小值,
π π 3π 25 14
则 4×2π+ ≤2ωπ+ <4×2π+ ,解得 ≤ω< .
2 6 2 6 3
学科网(北京)股份有限公司故选: B
8.
【答案】B
【解析】由图可知,两个函数图象都在 x 轴上方,所以 f′(x)>0,f (x) 单调递增,
所以实线为 f (x) 的图象,虚线为 f′(x) 的图象, f (0)=f′(0)=1 ,
对 A,y′=f′(x)+1>0,y=f (x)+x 单调递增,无最大值, A 错误;
ex[f (x)−f′(x)] e0[f (0)−f′(0)]
对
B,y′=
2
,y′|
x=0
=
2
=0
,
[f (x)] [f (0)]
由图可知,当 x<0 时, f (x)−f′(x)<0 ,当 x>0 时, f (x)−f′(x)>0 ,
ex
所以 y= 在 (−∞,0) 上单调递减,在 (0,+∞) 上单调递增,
f (x)
e0
所以当 x=0 时,函数取得最小值 y = =1 , B 正确;
min f (0)
对 C,y′=[f′(x)+f (x)]ex ,由图可知 f (x)+f′(x)>0 ,
所以 y=f (x)⋅ex 在 R 上单调递增,无最大值, C 错误;
f′(x)−f (x)
对 D , y′= ,由图可知,当 x<0 时, f (x)−f′(x)>0 ,
ex
f (x)
当 x>0 时, f (x)−f′(x)<0 ,所以函数 y= 在 (−∞,0) 上单调递增,在 (0,+∞) 上单调
ex
f (0)
递减,当 x=0 时,函数取得最大值 y = =1 , D 错误,故选: B
max e0
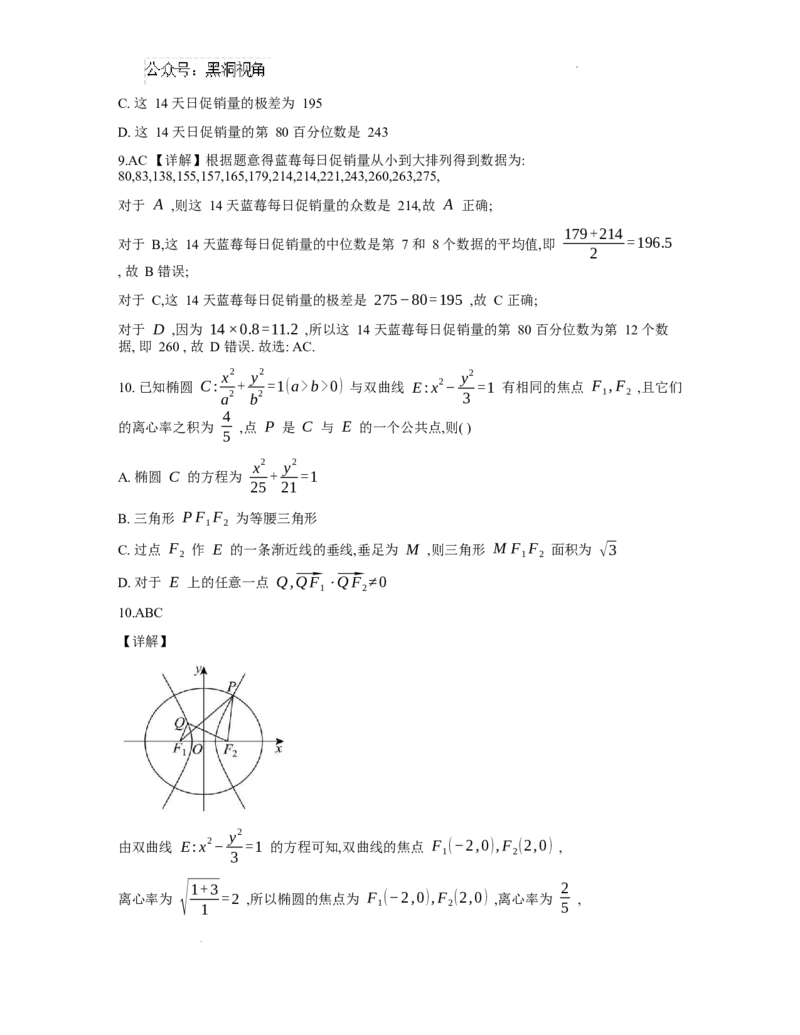
9. 某超市在两周内的蓝莓每日促销量如图所示, 根据此折线图, 下面结论正确的是( )
A. 这 14 天日促销量的众数是 214
B. 这 14 天日促销量的中位数是 196
学科网(北京)股份有限公司C. 这 14 天日促销量的极差为 195
D. 这 14 天日促销量的第 80 百分位数是 243
9.AC 【详解】根据题意得蓝莓每日促销量从小到大排列得到数据为:
80,83,138,155,157,165,179,214,214,221,243,260,263,275,
对于 A ,则这 14 天蓝莓每日促销量的众数是 214,故 A 正确;
179+214
对于 B,这 14 天蓝莓每日促销量的中位数是第 7 和 8 个数据的平均值,即 =196.5
2
, 故 B 错误;
对于 C,这 14 天蓝莓每日促销量的极差是 275−80=195 ,故 C 正确;
对于 D ,因为 14×0.8=11.2 ,所以这 14 天蓝莓每日促销量的第 80 百分位数为第 12 个数
据, 即 260 , 故 D 错误. 故选: AC.
x2 y2 y2
10. 已知椭圆 C: + =1(a>b>0) 与双曲线 E:x2− =1 有相同的焦点 F ,F ,且它们
a2 b2 3 1 2
4
的离心率之积为 ,点 P 是 C 与 E 的一个公共点,则( )
5
x2 y2
A. 椭圆 C 的方程为 + =1
25 21
B. 三角形 PF F 为等腰三角形
1 2
C. 过点 F 作 E 的一条渐近线的垂线,垂足为 M ,则三角形 M F F 面积为 √3
2 1 2
D. 对于 E 上的任意一点 Q,⃗QF ⋅⃗QF ≠0
1 2
10.ABC
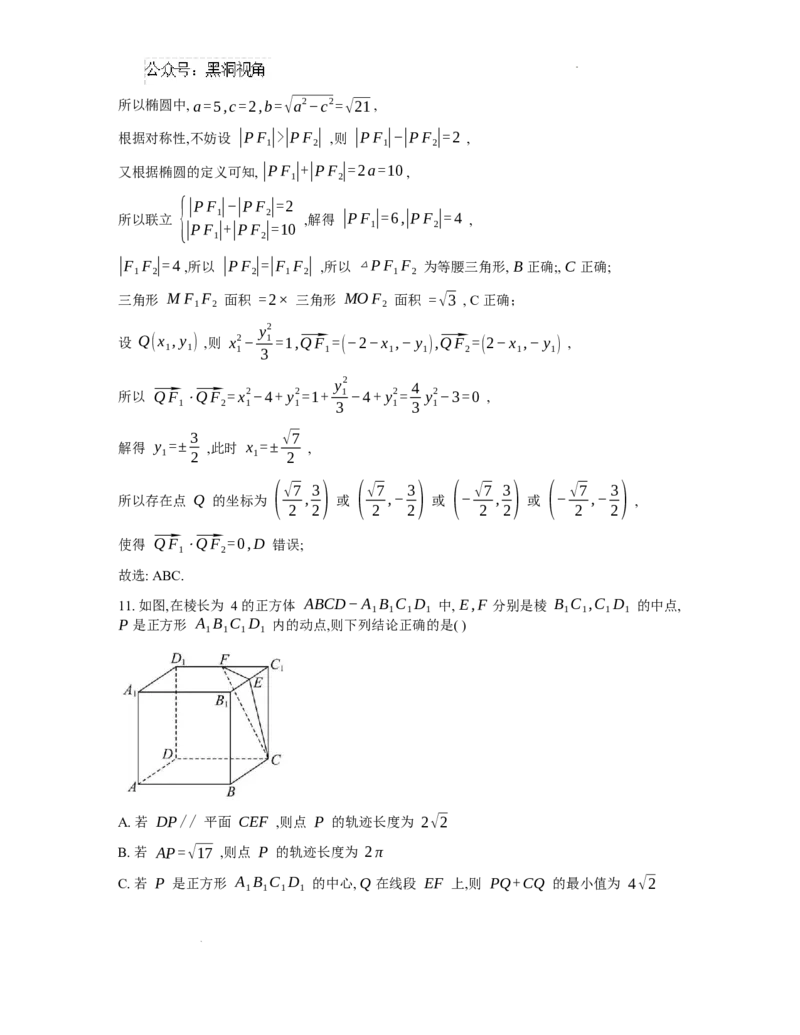
【详解】
y2
由双曲线 E:x2− =1 的方程可知,双曲线的焦点 F (−2,0),F (2,0) ,
3 1 2
√1+3 2
离心率为 =2 ,所以椭圆的焦点为 F (−2,0),F (2,0) ,离心率为 ,
1 1 2 5
学科网(北京)股份有限公司所以椭圆中, a=5,c=2,b=√a2−c2=√21 ,
根据对称性,不妨设 |PF |>|PF | ,则 |PF |−|PF |=2 ,
1 2 1 2
又根据椭圆的定义可知, |PF |+|PF |=2a=10 ,
1 2
{|PF |−|PF |=2
所以联立 1 2 ,解得 |PF |=6,|PF |=4 ,
|PF |+|PF |=10 1 2
1 2
|F F |=4 ,所以 |PF |=|F F | ,所以 △PF F 为等腰三角形, B 正确;, C 正确;
1 2 2 1 2 1 2
三角形 M F F 面积 =2× 三角形 MOF 面积 =√3 , C 正确;
1 2 2
y2
设 Q(x ,y ) ,则 x2− 1=1,⃗QF =(−2−x ,−y ),⃗QF =(2−x ,−y ) ,
1 1 1 3 1 1 1 2 1 1
y2
4
所以 ⃗QF ⋅⃗QF =x2−4+ y2=1+ 1−4+ y2= y2−3=0 ,
1 2 1 1 3 1 3 1
3 √7
解得 y =± ,此时 x =± ,
1 2 1 2
(√7 3) (√7 3) ( √7 3) ( √7 3)
所以存在点 Q 的坐标为 , 或 ,− 或 − , 或 − ,− ,
2 2 2 2 2 2 2 2
使得 ⃗QF ⋅⃗QF =0,D 错误;
1 2
故选: ABC.
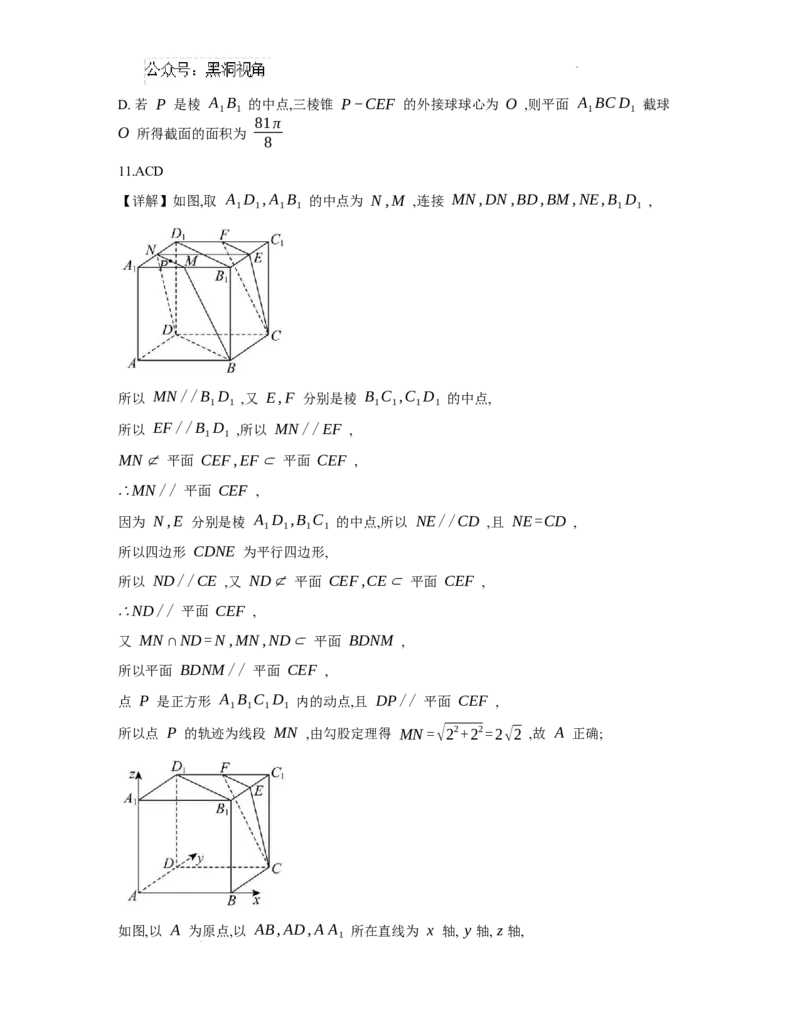
11. 如图,在棱长为 4 的正方体 ABCD−A B C D 中, E,F 分别是棱 B C ,C D 的中点,
1 1 1 1 1 1 1 1
P 是正方形 A B C D 内的动点,则下列结论正确的是( )
1 1 1 1
A. 若 DP// 平面 CEF ,则点 P 的轨迹长度为 2√2
B. 若 AP=√17 ,则点 P 的轨迹长度为 2π
C. 若 P 是正方形 A B C D 的中心, Q 在线段 EF 上,则 PQ+CQ 的最小值为 4√2
1 1 1 1
学科网(北京)股份有限公司D. 若 P 是棱 A B 的中点,三棱锥 P−CEF 的外接球球心为 O ,则平面 A BCD 截球
1 1 1 1
81π
O 所得截面的面积为
8
11.ACD
【详解】如图,取 A D ,A B 的中点为 N,M ,连接 MN,DN,BD,BM,NE,B D ,
1 1 1 1 1 1
所以 MN//B D ,又 E,F 分别是棱 B C ,C D 的中点,
1 1 1 1 1 1
所以 EF//B D ,所以 MN//EF ,
1 1
MN⊄ 平面 CEF,EF⊂ 平面 CEF ,
∴MN// 平面 CEF ,
因为 N,E 分别是棱 A D ,B C 的中点,所以 NE//CD ,且 NE=CD ,
1 1 1 1
所以四边形 CDNE 为平行四边形,
所以 ND//CE ,又 ND⊄ 平面 CEF,CE⊂ 平面 CEF ,
∴ND// 平面 CEF ,
又 MN∩ND=N,MN,ND⊂ 平面 BDNM ,
所以平面 BDNM// 平面 CEF ,
点 P 是正方形 A B C D 内的动点,且 DP// 平面 CEF ,
1 1 1 1
所以点 P 的轨迹为线段 MN ,由勾股定理得 MN=√22+22=2√2 ,故 A 正确;
如图,以 A 为原点,以 AB,AD,A A 所在直线为 x 轴, y 轴, z 轴,
1
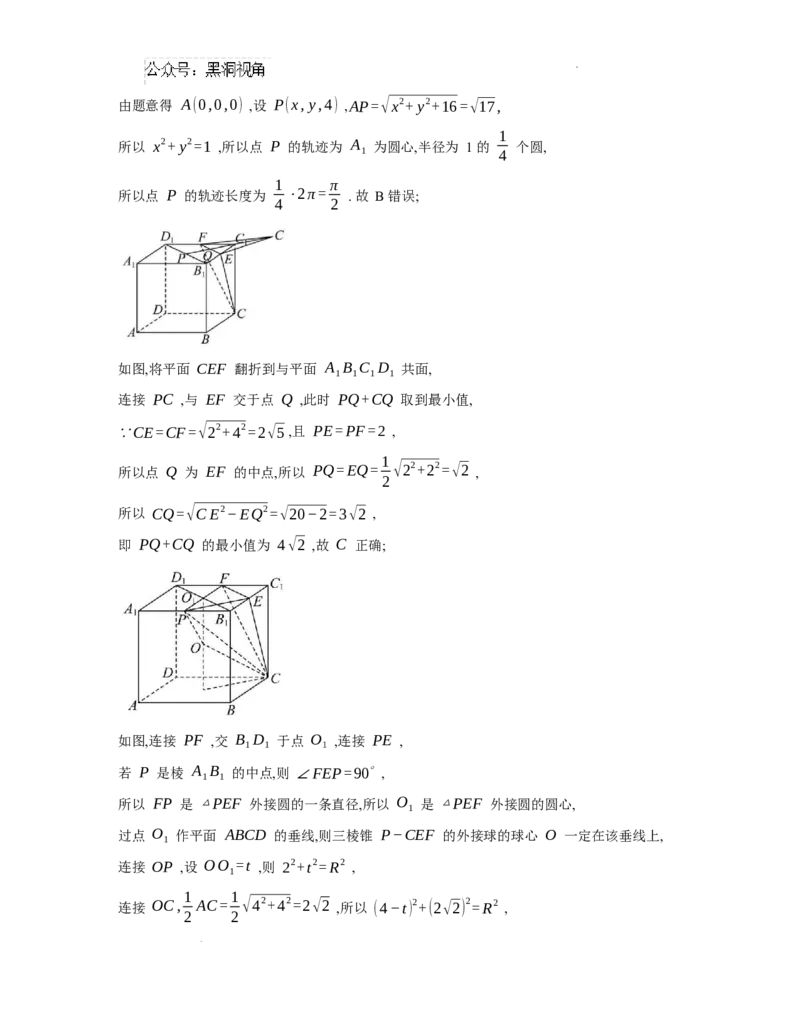
学科网(北京)股份有限公司由题意得 A(0,0,0) ,设 P(x,y,4) ,AP=√x2+ y2+16=√17,
1
所以 x2+ y2=1 ,所以点 P 的轨迹为 A 为圆心,半径为 1 的 个圆,
1 4
1 π
所以点 P 的轨迹长度为 ⋅2π= . 故 B 错误;
4 2
如图,将平面 CEF 翻折到与平面 A B C D 共面,
1 1 1 1
连接 PC ,与 EF 交于点 Q ,此时 PQ+CQ 取到最小值,
∵CE=CF=√22+42=2√5 ,且 PE=PF=2 ,
1
所以点 Q 为 EF 的中点,所以 PQ=EQ= √22+22=√2 ,
2
所以 CQ=√CE2−EQ2=√20−2=3√2 ,
即 PQ+CQ 的最小值为 4√2 ,故 C 正确;
如图,连接 PF ,交 B D 于点 O ,连接 PE ,
1 1 1
若 P 是棱 A B 的中点,则 ∠FEP=90∘ ,
1 1
所以 FP 是 △PEF 外接圆的一条直径,所以 O 是 △PEF 外接圆的圆心,
1
过点 O 作平面 ABCD 的垂线,则三棱锥 P−CEF 的外接球的球心 O 一定在该垂线上,
1
连接 OP ,设 OO =t ,则 22+t2=R2 ,
1
1 1
连接 OC, AC= √42+42=2√2 ,所以 (4−t) 2+(2√2) 2=R2 ,
2 2
学科网(北京)股份有限公司