广东实验中学2024—2025学年（下）期中考试（问卷）(最新版）_2024-2025高二（7-7月题库）_2025年05月试卷_0519广东实验中学2024-2025学年高二下学期期中考试

广东实验中学 2024—2025 学年（下）高二级期中考试 数 学 命题：高二数学备课组 审定：夏嵩雪 校对：高二数学备课组 本试卷共4页，满分150分，考试用时120分钟． 注意事项： 1．答卷前，考生务必用黑色字迹的钢笔或签字笔将自己的姓名、考号填写在答题卷上。 2．选择题每小题选出答案后，用2B铅笔把答题卷上对应题目的答案标号涂黑；如需改动， 用橡皮擦干净后，再选涂其它答案；不能答在试卷上。 3．非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在答题卷各题目指定区域内的 相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改 液。不按以上要求作答的答案无效。 4．考生必须保持答题卡的整洁，考试结束后，将答题卷收回。 第一部分选择题（共58分） 一、选择题：本题共 8小题，每小题 5分，共 40分。在每小题给出的四个选项中， 只有一项是符合题目要求的。 1. 下列求导运算正确的是（ ） A.    cos π 3     sin 3 π B.    1 x      x 1 2 C.  log 2 x   xl 1 n2 D.  3x  3x z 2．已知复数z满足 i，则 z （ ） z1 3 2 A． B． 3 C． D． 2 2 2         3.已知向量a,b，其中，| ,|b|2，且(ab)a，则向量a和b 的夹角是（ ）  |= 3 2 5 A． B． C． D． 6 3 3 6 4．一个底面边长为2cm的正四棱柱形状的容器内装有一些水（底面放置于桌面上），现将一 个底面半径为1cm的铁制实心圆锥放入该容器内，圆锥完全沉入水中且水未溢出，并使得水 π 面上升了 cm.若该容器的厚度忽略不计，则该圆锥的侧面积为（ ） 2 A． 37πcm2 B．6πcm2 高二数学 第 1 页，共 4 页C．2 10πcm2 D．2 37πcm2 5．已知抛物线C: y2 4x的焦点为F，准线为l，点A在C上，过A作l的垂线，垂足为A ， 1 若| AF| AF ，则| AF | 1 A．2 B．4 C．6 D．8 6.已知 ,若 的展开式中所有项的二项 式系数和为16，n 则 n ( )3 2 n 2 −1 = n +…+ 3 + 2 + 1 + 0 2 −1 A.40 B.41 C. D. 2+ 4 = 7. 学校将从4男4名女中选出4人分别担任辩论赛 −4 中 0 的一、二、三、四辩 − 手 41 ，其中男生甲不 适合担任一辩手，女生乙不适合担任四辩手．要求甲乙同时入选或同时不入选．不同组队形 式有（ ）种． A. 360 B.480 C.540 D.570 ' ' 8. 已 知 函数 f(x) 及 其 导函 数 f (x) 的 定 义 域均 为 R ， 记 g(x) f (x1) ， 且 ' f(2x) f(2x)4x，g(x3）为偶函数，则g (7) g(25)＝（ ） A．0 B．1 C．1 D．2 二、选择题：本题共 3小题，每小题 6分，共18分。在每小题给出的选项中，有 多项符合题目要求。全部选对的得 6 分，部分选对的得部分分，有选错的得 0分。 9.已知在首项为 1，公差为 d 的等差数列a 中，a 、a 、a 是等比数列b 的前三项， n 1 2 6 n 数列a 的前 n 项和为S ，则（ ） n n n2n1 S  A．d  0或d 3 B．S  C． n是等差数列 D．b 4n1 n 2  n  n 10．如下图，棱长为2的正方体ABCDABCD 中，E为棱DD 的中点，F 为正方形CCDD 1 1 1 1 1 1 1 内一个动点（包括边界），且BF //平面ABE，则下列说法正确的有（ ） 1 1 1 A．动点F 轨迹的长度为 2 B．三棱锥B DEF 体积的最小值为 1 1 3 C．BF与AB不可能垂直 D．三棱锥A BEF的体积为定值 1 1 1 高二数学 第 2 页，共 4 页11．已知函数 f(x)x3mx2，x2是函数 f(x)的一个极值点，则下列说法正确的是（ ） A．m3 B．函数 f(x)在区间(0,2)上单调递减 C．过点(1,2)只能作一条直线与y f(x)相切 D．函数y f[f(x)]2恰有4个零点 第二部分非选择题（共92分） 三、填空题：本题共 3小题，每小题 5分，共 15 分。 12.若函数 恰有三个零点，则实数 的取值范围是 2 ( )= − 13. 的展开式中 的系数 2 5 3 3 14.已 知−圆 : + =1，点 M 在 上，过点M 作圆C的两条切线，切点分别为A 2 2 2 和B，以A B(为x−直2径)作+圆 C，则圆C 的=面 积的最小值为 四、解答题：本题共 5小题，共 77分。解答应写出文字说明、证明过程或演算步 骤。  AC 15.（13分）已知∆ABC的内角A,B,C的对边分别是a,b,c，已知4cos2   4sinAsinC3 .  2  (1)求角B的大小； (2)若D为AC上一点，且AD2,DC 1，BD为ABC的角平分线，求线段BD的长. 16.（15分）设数列a 的前n项和为S ，已知a 1，a S 1(nN*). n n 1 n1 n （1）求数列a 的通项公式； n  1  （2）若a ，b，b ，…b ，a 组成一个n2项的等差数列，记其公差为d ，求数列  n 1 2 n n1 n d  n 的前n项和T . 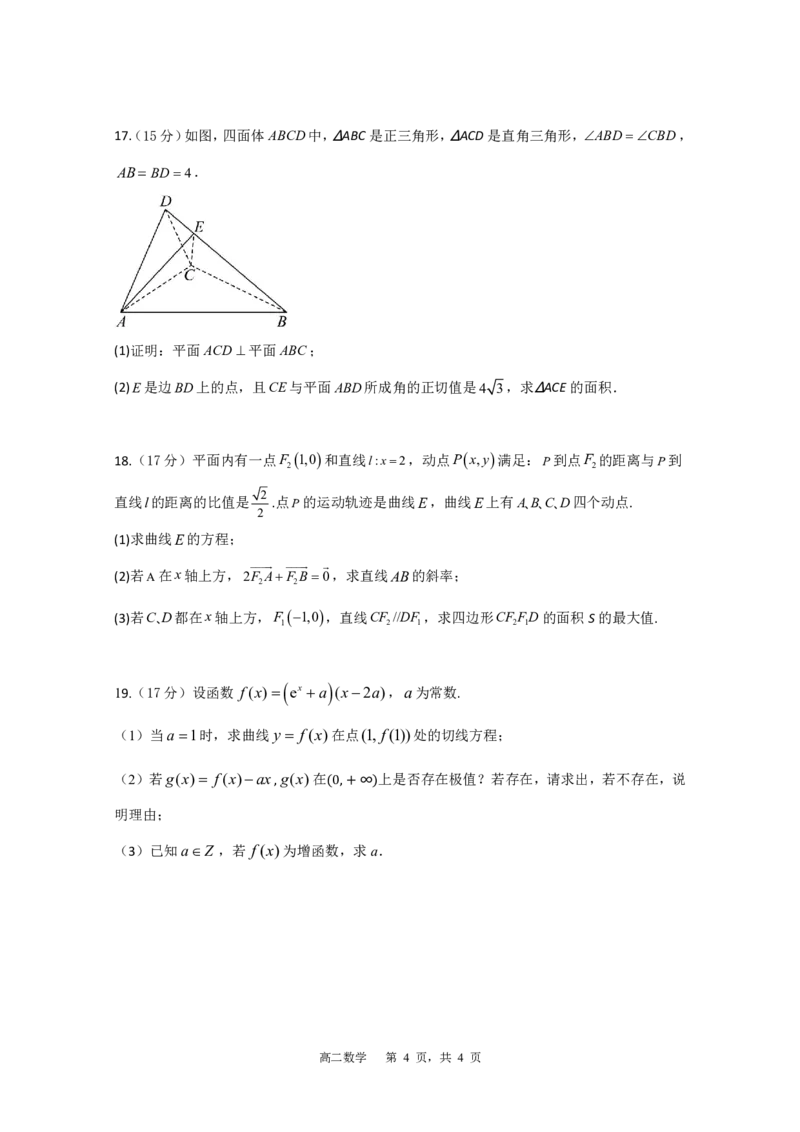n 高二数学 第 3 页，共 4 页17（. 15分）如图，四面体ABCD中，∆ABC是正三角形，∆ACD是直角三角形，ABDCBD， AB BD4． (1)证明：平面ACD 平面ABC； (2)E是边BD上的点，且CE与平面ABD所成角的正切值是4 3，求∆ACE的面积． 18.（17分）平面内有一点F 1,0和直线l:x2，动点Px,y满足：P到点F 的距离与P到 2 2 2 直线l的距离的比值是 .点P的运动轨迹是曲线E，曲线E上有A､B､C､D四个动点. 2 (1)求曲线E的方程；    (2)若A在x轴上方，2F AF B0，求直线AB的斜率； 2 2 (3)若C､D都在x轴上方，F 1,0，直线CF //DF ，求四边形CF FD的面积S的最大值. 1 2 1 2 1   19.（17分）设函数 f(x) ex a (x2a)，a为常数 . （1）当a 1时，求曲线y f(x)在点(1, f(1))处的切线方程； （2）若g(x) f(x)ax g(x)在 ∞ 上是否存在极值？若存在，请求出，若不存在，说 明理由； , (0,+ ) （3）已知aZ ，若 f(x)为增函数，求a． 高二数学 第 4 页，共 4 页