广东实验中学2024—2025学年（下）期中考试（问卷）(最新)参考答案_2024-2025高二（7-7月题库）_2025年05月试卷_0519广东实验中学2024-2025学年高二下学期期中考试

广东实验中学 2024—2025 学年（下）高二级期中考试 数学参考答案 1.C 2.C 3.A． 4.A 5.B 6.A 7.D 8.D 9.AC 10.ABD 11.ABC 12. 4 13. 5 14. 4 (0, 2 )  5 【注意】建议解答题评分时，每道题都按照满分无瑕疵的原则。 7. 解析：甲乙同时入选时，按甲担任四辩手或担任二、三辩手分类求解，甲乙同时不入选时，直接从6人中选4 人排列即可得．因此所求方法数为C2A3 C1C1A2 A4 570 6 3 2 2 6 6 8.解：因为g（3+x）为偶函数，g（x）＝f′（x+1），所以f′（x+4）＝f′（﹣x+4）， 对f（2+x）﹣f（2﹣x）＝4x两边同时求导，得f′（2+x）+f′（2﹣x）＝4， 所以有f′（4+x）+f′（﹣x）＝4 f′（4﹣x）+f′（﹣x）＝4 f′（4+x）+f′（x）＝4 f′（8+x⇒）＝f′（x），所以函数f′（⇒x）的周期为8， 在f′（2+x）+f′（2﹣x）＝⇒4中，令x＝0，所以f′（2）＝2， 因此g（25）＝f′（26）＝f′（2）＝2，因为g（3+x）为偶函数， 所以有g（3+x）＝g（3﹣x） g′（3+x）＝﹣g′（3﹣x） g′（7）＝﹣g′（﹣1） （1）， f′（8+x）＝f′（x） g（7+⇒x）＝g（x﹣1） g′（7+x）＝⇒g′（x﹣1） g′（7）＝g′（﹣1）（2），由（1）， （2）可得：g′（7）⇒＝0，所以g′（7）-g（⇒25）＝-2，故选：D． ⇒ 9.【答案】AC【详解】由题意a2 aa ，则(1d)215d ，整理得d2 3d 0，可得d  0或d 3，当d  0 2 1 6 S S  n(3n1) 时，a 1，S n，则 n 1，即 n是等差数列，此时b 1；当d 3时，a 3n2，S  ， n n n  n  n n n 2 S 3n1 S  则 n  ，即 n是等差数列， n 2  n  此时b 1,b 4,b 16，易知公比为 4，故b 4n1；综上，A、C 对，B、D 错. 1 2 3 n 11．ABC【详解】对于A中，由函数 f xx3mx2，可得 fx3x22mx， 因为x2 是函数 f x的一个极值点，可得 f23222m20， 解得m3，经检验适合题意，所以A正确； 对于B中，由 f(x)3x(x2)，令 f(x)0，解得x 0或x 2， 1 2 当x(,0)时， f(x)0；当x(0,2)时， f(x)0；当x2,时， f(x)0， 故 f x在区间(,0)上递增，在区间(0,2)上递减，在区间(2,)上递增，所以B正确； 对于C中，设过点(1,2)且与函数y f(x)相切的切点为x ,y ， 0 0 1则该切线方程为y fx x12  3x26x x12， 0 0 0 由于切点x ,y 满足直线方程，则 f x   3x26x x 12 x33x2， 0 0 0 0 0 0 0 0 整理得2x 1 x2 2x 1  0，解得x 1，所以只能作一条切线，所以C正确； 0 0 0 0 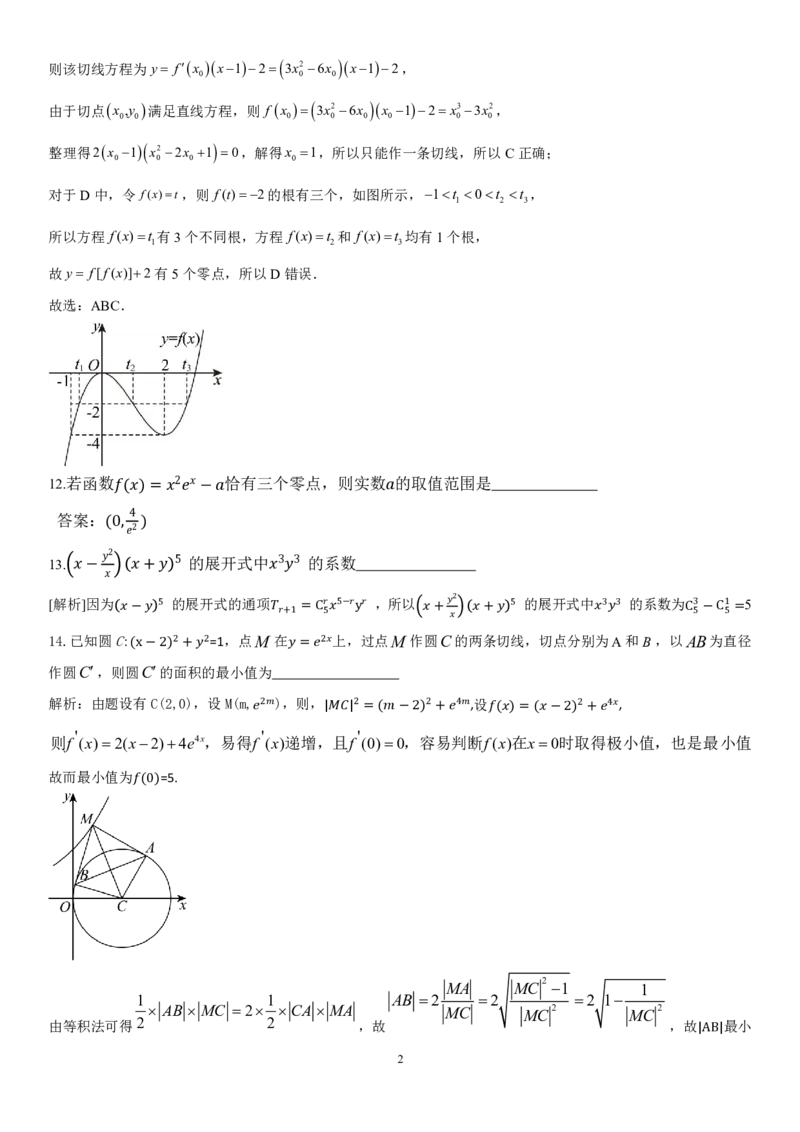对于D中，令 f(x)t，则 f(t)2的根有三个，如图所示，1t 0t t ， 1 2 3 所以方程 f(x)t 有3个不同根，方程 f(x)t 和 f(x)t 均有1个根， 1 2 3 故y f[f(x)]2有5个零点，所以D错误． 故选：ABC． 12.若函数 恰有三个零点，则实数 的取值范围是 2 答案： ( ) = − 4 2 (0, ) 13. 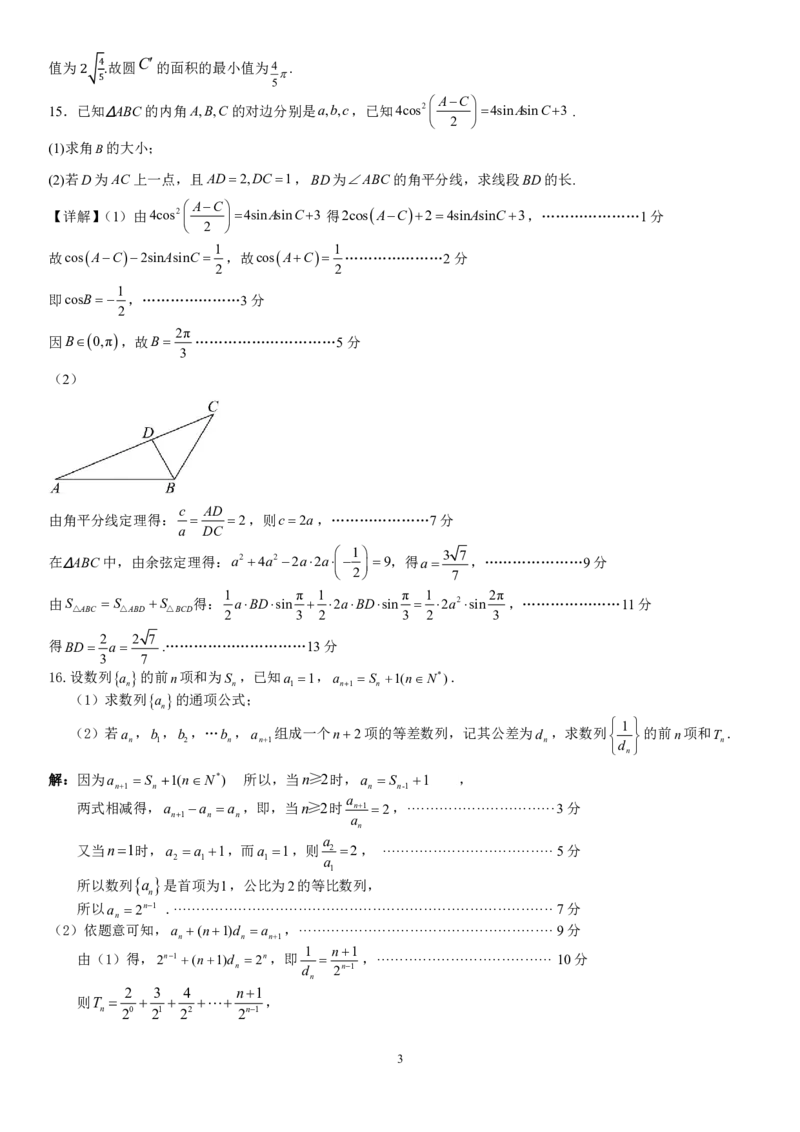的展开式中 的系数 2 5 3 3 [解析 ] − 因为 + 的展开式的通项 ，所以 的展开式中 的系数为 5 2 5 5− 5 3 3 3 1 14.已知圆C :− =1，点M 在 +1 =C5 上，y过点M 作 圆+ C 的两 条+切 线，切点分别 为 A和B，以C A 5 B −为C直 5 =径 2 2 2 作圆C，则圆(xC−2的)面+积 的最小值为 = 解析：由题设有C(2,0)，设M(m, )，则， ,设 , 2 2 2 4 2 4 ' ' | | '=( −2) + ( )=( −2) + 则f (x)2(x2)4e4x，易得f (x)递增，且f (0)0，容易判断f(x)在x0时取得极小值，也是最小值 故而最小值为 =5. (0) MA MC 2 1 1 1 1 AB 2 2 2 1  AB  MC 2  CA MA MC MC 2 MC 2 由等积法可得2 2 ，故 ，故 最小 2 |AB|值为 .故圆C 的面积的最小值为4  4 5 2 5 .  AC 15．已知∆ABC的内角A,B,C的对边分别是a,b,c，已知4cos2   4sinAsinC3 .  2  (1)求角B的大小； (2)若D为AC上一点，且AD2,DC 1，BD为ABC的角平分线，求线段BD的长. 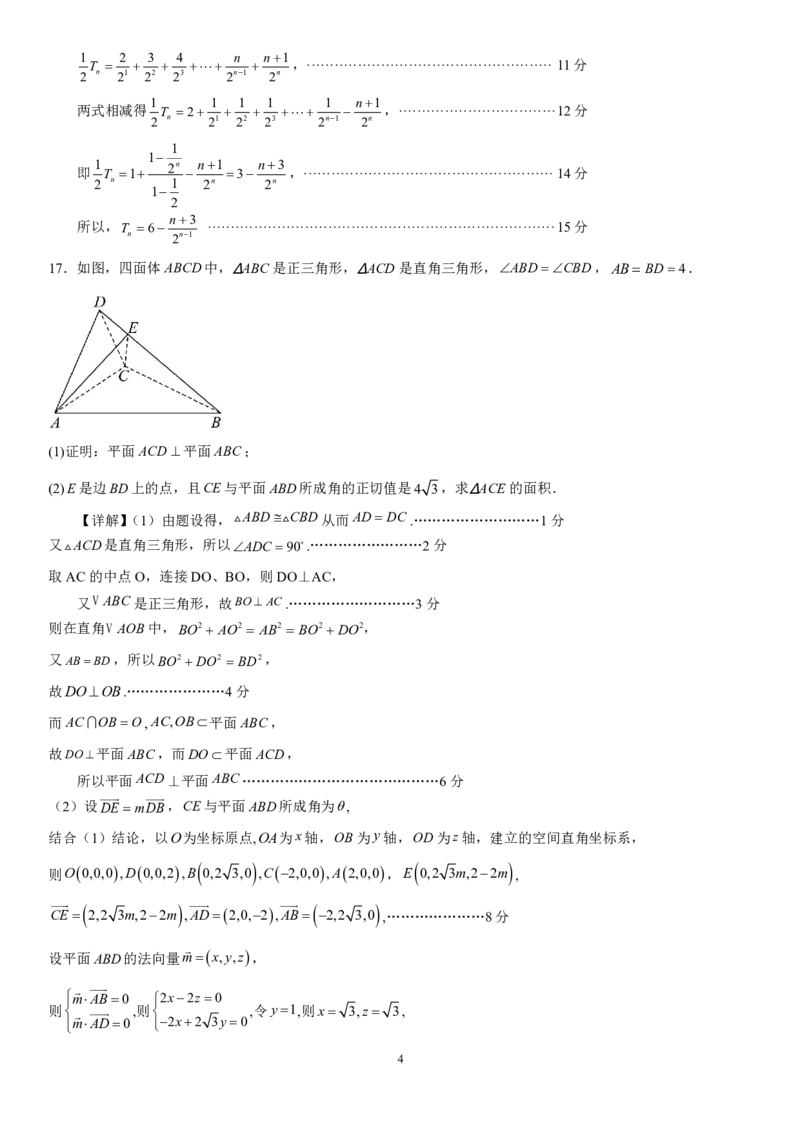 AC 【详解】（1）由4cos2   4sinAsinC3 得2cosAC24sinAsinC3，…………………1分  2  1 1 故cosAC2sinAsinC  ，故cosAC …………………2分 2 2 1 即cosB ，…………………3分 2 2π 因B0,π，故B …………………………5分 3 （2） c AD 由角平分线定理得：  2，则c2a，…………………7分 a DC  1 3 7 在∆ABC中，由余弦定理得：a24a22a2a  9，得a ，…………………9分  2 7 1 π 1 π 1 2π 由S  S S 得： aBDsin  2aBDsin  2a2sin ，…………………11分 △ABC △ABD △BCD 2 3 2 3 2 3 2 2 7 得BD a .…………………………13分 3 7 16.设数列a 的前n项和为S ，已知a 1，a S 1(nN*). n n 1 n1 n （1）求数列a 的通项公式； n  1  （2）若a ，b，b ，…b ，a 组成一个n2项的等差数列，记其公差为d ，求数列 的前n项和T . n 1 2 n n1 n d  n n 解：因为a S 1(nN*) 所以，当n≥2时，a S 1 ， n1 n n n-1 a 两式相减得，a a a ，即，当n≥2时 n1 2，································3分 n1 n n a n a 又当n1时，a a 1，而a 1，则 2 2， ·····································5分 2 1 1 a 1 所以数列a 是首项为1，公比为2的等比数列， n 所以a 2n1 .··················································································7分 n （2）依题意可知，a (n1)d a ，·······················································9分 n n n1 1 n1 由（1）得，2n1 (n1)d 2n，即  ，······································ 10分 n d 2n1 n 2 3 4 n1 则T     ， n 20 21 22 2n1 31 2 3 4 n n1 T      ，····················································· 11分 2 n 21 22 23 2n1 2n 1 1 1 1 1 n1 两式相减得 T 2     ，··································12分 2 n 21 22 23 2n1 2n 1 1 即 1 T 1 2n  n1 3 n3 ，······················································14分 2 n 1 2n 2n 1 2 n3 所以，T 6 ···········································································15分 n 2n1 17．如图，四面体ABCD中，∆ABC是正三角形，∆ACD是直角三角形，ABDCBD，AB BD4． (1)证明：平面ACD 平面ABC； (2)E是边BD上的点，且CE与平面ABD所成角的正切值是4 3，求∆ACE的面积． 【详解】（1）由题设得，ABDCBD从而ADDC.………………………1分 又ACD是直角三角形，所以ADC90.……………………2分 取AC的中点O，连接DO、BO，则DO⊥AC， 又V ABC是正三角形，故BOAC.………………………3分 则在直角V AOB中，BO2 AO2  AB2  BO2DO2， 又ABBD，所以BO2DO2 BD2， 故DOOB.…………………4分 而ACOBO,AC,OB平面ABC， 故DO平面ABC，而DO平面ACD， 所以平面ACD⊥平面ABC……………………………………6分   （2）设DE mDB，CE与平面ABD所成角为, 结合（1）结论，以O为坐标原点,OA为x轴，OB为y轴，OD为z轴，建立的空间直角坐标系， 则O0,0,0,D0,0,2,B  0,2 3,0  ,C2,0,0,A2,0,0，E  0,2 3m,22m  ,    CE  2,2 3m,22m  ,AD2,0,2,AB  2,2 3,0  ,…………………8分  设平面ABD的法向量mx,y,z，    mAB0 2x2z0 则   ,则 ,令y1,则x 3,z 3, mAD0 2x2 3y0 4   故m 3,1, 3 ,,…………………10分 4 3 由tan4 3,则sin …………………11分 7 m  C  E  2 3 3m2 3 22m 4 3 故sin     …………………12分 m CE 313 412m241m2 7 1 则16m28m10,解得m …………………13分 4   3 3    3 3 故CE 2, , ,AC 4,0,0,AE 2, , ,      2 2  2 2    则 CE  7, AC 4, AE  7, 所以AC边上的高为 3, 1 故S  4 32 3.……………………………………15分 ACE 2 18.平面内有一点F 1,0和直线l:x2，动点Px,y满足：P到点F 的距离与P到直线l的距离的比值是 2 .点P的 2 2 2 运动轨迹是曲线E，曲线E上有A､B､C､D四个动点. (1)求曲线E的方程；    (2)若A在x轴上方，2F AF B0，求直线AB的斜率； 2 2 (3)若C､D都在x轴上方，F 1,0，直线CF //DF，求四边形CF FD的面积S的最大值. 1 2 1 2 1 x2 14 答案：(1) y2 1(2) (3) 2 2 2 2 解：（1）由题意 (x1)2  y2  x2 ， 2 x24x4 x2 两边平方得x22x1y2  ，化简得 y2 1， 2 2 x2 所以曲线E的方程为 y2 1；………………3分 2      （2）2F AF B0，即F B2F A，则直线AB的斜率是正数，………………4分 2 2 2 2 1 设l :xky1，直线AB的斜率为 k 0，………………5分 AB k xky1  设 ，联立x2 ，  y2 1  2 化简得  k22  y22ky10，所以y y  2k ,y y  1 ，………………7分 1 2 k22 1 2 k22 由题意知y 2y ， 2 1 2k 1 代入y y ,y y ，消y ，可得y  ,2y2  ， 1 2 1 2 2 1 k22 1 k22 52 14 k  解得 7 ，所以直线AB的斜率是 2 ；………………10分 （3）延长CF ，交椭圆于点G， 2 CF //DF，由对称性可知GF DF ，△FGF 和∆CD 等底等高，所以面积相等， 2 1 2 1 1 2 1 1 四边形CF FD的面积S S   FF y y  y y ，………………12分 2 1 GCF1 2 1 2 C G C G 2k 1 设l :xk y1，由（2）知y y  1 ,y y  ， CD 1 C G k22 C G k22 1 1 8k28 8k28 所以y y  y y 2  y y 24y y  1 ，即S  1 ，………………14分 C G C G C G C G k22 k22 1 1 8k28 2 2t 2 2 1    2 令 k 1 21t,t1，所以 k 1 22 t21 t 1 ，………………16分 t 当且仅当t1即k 0时，S取到最大值 2，此时C､D分别在F､F正上方.………………17分 1 2 1 19. 设函数 f(x)  ex a  (x2a)，a为常数 . （1）当a 1时，求曲线y f(x)在点(1, f(1))处的切线方程； （2）若g(x) f(x)ax 求g(x)的极值； , （3）已知aZ ，若 f(x)为增函数，求a． ．解：（1）当a 1时， f(x)  ex 1  (x2)，则 f(x)(x1)ex 1，  f(1)e1，切点为(1,e1)，切线斜率为 f(1)1， （2）切线方程为y f(1) f (1)(x1)，整理得，y xe2………… 分 （说明：本小问共4分，求导2分，整理得到切线方程2分） 4 g(x)(x2a1)ex，………… 分 当2a10时，g(x)0,g(x)递增5，无极值；………… 分 6 当 2a10时，g(x)0得x2a1, 6g(x)0得x2a1 g(x)0得x2a1，………… 分 , 7 所以g(x)在(0，2a1)单调递减，在(2a1,)单调递增………… 分 8 所以x2a1时g(x)有极小值g(2a1)e2a12a2，无极大值.………… 分 综上： 当 2a10时，g(x)无极值； 9 当2a10时，g(x)有极小值e2a12a2，无极大值.………… 分 说明：本小问 分，极小值没化简或未说明无极大值，共扣 分 10 (（3） f(x)(x52a1)ex a,f(x)为增函数， f(x)(x21a1))exa0 恒成立，………… 分 11 方法1：令g(x)(x2a1)exa,aZ， 则g(x)(x2a2)ex 0，………… 分 当x(,2a2)时，g(x)0,g(x)单 1 调 2 递减， 当x(2a2,)时，g(x)0,g(x)单调递增，………… 分 当x  2a2时，g(x)取得极小值，也是最小值， 13 g(2a2)e2a2a0 ，………… 分 14 1 令h(x)e2x2x ，令h(x)2e2x210，解得x1 ln2， 2  1  当x  ,1 ln2 时，h(x)0,h(x)单调递增，  2   1  当x 1 ln2,  时，h(x)0,h(x)单调递减，  2   1  1 1 又h1 ln2   ln20, h(1)0, h(0)e2 0, h(2)2e2 0，  2  2 2 ………… 分 a 1．… 16 ……… 分 17 2a （3）方法 2： f(0)12aa1a0, f(1) a0，解得0a1,aZ,a0，或a 1， e 当a  0时， f(x)(x1)ex，易知 f(2)e20，不符题意； 7当a 1时， f(x)(x1)ex 1，设g(x)(x1)ex1，则g(x) xex， 当x(,0)时，g(x)0,g(x)单调递减， 当x(0,)时，g(x)0,g(x)单调递增， 当x  0时，g(x)取得极小值，也是最小值，g(x) g(0)0，符合题意； （说明：必要性探路得0 a 1 2分，后面略 分析判断得a  0，或a 1 2分， 验证a  0 2分，验证a 1 2分，结论1分． 若由 f(0)0, f(2)0,aZ直接得a 1，再去验证a 1，酌情给分） 8