四川省名校联盟2025届高三12月联考数学答案_2024-2025高三（6-6月题库）_2024年12月试卷_1218四川省名校联盟2025届高三12月联考试卷（全科）

四川省名校联盟 12 月联考 数学参考答案 一、单选题(本题共8小题，每小题5分，共40分.) B D B A C A D C 二、多选题(本题共3小题，每小题6分，共18分.) 9.AD 10.ABD 11.ACD 三、填空题(本题共3小题，每小题5分，共15分.) 12. 1 x 4 2 + y 2 = 1 13. 4 6 14. 1 1 9 ； 5 9 9  S n  1 1 8 四、解答题(本题共5小题，共77分.) 15.解：(1) ∵m∥n，∴ 3 a s i n C = c + c c o s A ， ……………………………..……………..2分 ∴ 3 s i n A s i n C = s i n C + s i n C c o s A . ∵ s i n C  0 ，∴ 3 s i n A − c o s A = 1 ， ………...………………………………..…………..4分 即 s i n ( A 6 ) 1 2  − = . ∵ A ( 0 , )   ， ∴ A 6 6   − = ，∴ A 3  = . ……………………………………..……………..………….…..6分 (2) 在ABD中，由正弦定理得 s A i n D B = s i n B  D B A D ，∴ B 1 D = A D s i n s i B n 3 0 = 2 s i n B . ………8分 同理  A C D 中有 C 1 D = 2 s i n C ， ∴ B 1 D + C 1 D = 2 ( s i n B + s i n C ) . ………………………………………...10分 ∵ A 3  = 2 ，B+C = ， 3 2  ∴2(sinB+sinC)=2[sinB+sin( −B)]=2 3sin(B+ ). ………………..12分 3 6 2  1 ∵B(0, )，∴sin(B+ )( ,1]， 3 6 2∴ 2 B 1 D + C 1 D 的范围为 ( 3 ， 2 3 ] . ………………………………………..……..13分 16.解(1)∵圆C 与圆 1 C 相切于 N ( 0 ， 2 ) ，且过点 M ( − 1 ， 3 ) ， ∴圆 C 1 与圆C外切，且圆心在直线CN 上. …………………….………………………………….2分 设圆心 C 1  r =2−b (0,b)，半径为r，则 ，………………………………………………………4分 1+(b− 3)2 =r2 b=0 解得 . r =2 ∴圆C 的标准方程为x2 + y2 =4. ………………………………..………………………………………6分 1 (2) 【方法一】由题意可知，直线 l 的斜率不为0， 设直线 l 的方程为： x + 1 = t ( y + 2 ) ，即 x − t y + 1 − 2 t = 0 ,……………..…………………………………8分 设圆心 C 1 到直线 l 的距离为 d ，则 d = 1 − 1 + 2 t 2 t = 2 2 − ( 3 ) 2 = 1 ，…………...........................……….10分 解得 t = 0 ，或 t = 4 3 ，..………………………………………………….……………………………………13分 直线 l 的方程为 x + 1 = 0 ，或 3 x − 4 y − 5 = 0 ....……………………………………………………………15分 【方法二】设圆心C 到直线 1 l 的距离为 d ，则 d = 2 2 − ( 3 ) 2 = 1 ，………………….………………8分 ① 直线 l 的斜率不存在时， l 的方程为 x = − 1 ，此时圆心 C 1 到直线 l 的距离为 d = 1 ，符合题 意. ……………………………………………………………………………..…………………………10分 ② 直线 l 的斜率存在时，设为 k ，则直线 l 的方程可表示为 k x − y + k − 2 = 0 ， d = k 1 − + 2 k 2 = 1 3 ，解得k = ，………………………………………………………….……………13分 4 直线 l 的方程为3x−4y−5=0.……………………………………………………….....……………14分 综上①②，直线l的方程为x+1=0，或 3 x − 4 y − 5 = 0 . ………………………………….………15分 17.(1)解 f ' ( x ) = 2 − c o 1 s 2 x ， …………………………………………………………………………2分    令 f'(x)＞0，解得0＜x＜ ；令 f'(x)＜0，解得 ＜x＜ ， …………………..…………….4分 4 4 2故 3 f ( x ) 单调递增区间为 ( 0 , 4 )    ，单调递减区间为( , ). ………………….……….………..6分 4 2 (2) 【方法一】证明：x＞0，a2，  a x  2 x ，  f ( x )  2 x − t a n x ， …………….….…..8分 要证明 f ( x )  s i n 2 x ，则只需证明2x−tanxsin2x， 令 g ( x ) = 2 x − t a n x − s in 2 x ， ( 0 , 2 )  x  ， ……………………………………………….…..10分 1 1 g'(x)=2− −2cos2x=4−(4cos2 x+ )， cos2 x cos2 x  x(0, ) 2  c o s 2 x  ( 0 ,1 ) ，  4 c o s 2 x + c o 1 s 2 x  4 ，当且仅当 c o s 2 x = 1 2  ( 0 ,1 ) 时，上式等号成立， …………………..12分 当 ( 0 , 2 )  x  时， g ' ( x )  0 ，  g ( x ) 在区间 ( 0 , 2 )  上单调递减， ……………………….....13分 g(x)g(0) =0，即 2 x − t a n x ＜ s in 2 x ， 当 ( 0 , 2 )  x  时， f ( x )  s in 2 x 得证. ……………………………………………….……..15分 【方法二】证明：令g(x)=ax−tanx−sin2x， ( 0 , 2 )  x  ， ……………………………….....8分 g ' ( x ) = a + 2 − ( 4 c o s 2 x + c o 1 s 2 x ) ， ……………………………………………………….……..10分  x(0, ) ， 2  c o s 2 x  ( 0 ，1 ) ， 1 4cos2 x+ 4，当且仅当 cos2 x c o s 2 x = 1 2  ( 0 ，1 ) 时，上式等号成立， …………………..12分 g'(x)a+2−4=a−2， 又  a  2  ，当x(0, )时，g'(x)0， 2 g ( x )  在区间(0, )上单调递减， ……………..13分 2 g(x)g(0) =0，当 4 ( 0 , 2 )  x  时， f ( x )  s in 2 x 得证. ………………………..………………………...…..15分 18.(1)证明：∵ A B / / C D ， A B ⊥ B C ∴ C D ⊥ B C . ………………………..1分 又∵平面 P C D ⊥ 平面 A B C D ，且平面 P C D  平面ABCD=CD， B C  平面 A B C D ， ∴BC ⊥平面PCD. ∵ D E  平面 P C D ， ∴BC ⊥DE. ……….……..……..3分 ∵正三角形 P C D 中 E 为 P C 中点，∴ D E ⊥ P C . ∵ B C  P C = C ，∴ D E ⊥ 平面 P B C . ∵ P B  平面 P B C ，∴ D E ⊥ P B . ……………….……..5分 ∵ E F ⊥ P B ，且 E F  D E = E ， ∴PB⊥平面DEF. ………….……..6分 (2) 由(1)知 P B ⊥ 平面 D E F ，∵ D F  平面 D E F ，∴ P B ⊥ D F . 又∵ E F ⊥ P B ， ∴  D F E 为平面PBD与平面 P B C 的夹角(或其补角)， ….……………..7分 由(1)知 D E ⊥ 平面 P B C ，∴ D E ⊥ E F . ∵ A B ⊥ B C 且 A B = B D = 2 C D = 4 ， ∴ B C = 2 3 ， B D C 3   = . ∴在正  P C D 中， P C = 2 ，DE = 3. 由(1)知BC ⊥平面PCD，∵PC 平面DEF， ∴ B C ⊥ P C . …………………………..……………..9分 ∴  P C B 为直角三角形. ∵ P C = 2 , B C = 2 3 ，∴ P B = 4 . ∵ E 是PC 中点，且 E F ⊥ P B ， ∴  P E F ∽  P B C EF PE ，∴ = ， BC PB 3 解得EF = . ………………………………………………………………………………………..11分 2 15 EF 5 ∴在RtDEF中，DF = DE2 +EF2 = ，∴cosDFE = = . 2 DF 5∴平面 5 P B D 与平面 P B C 的夹角的余弦值为 5 5 . 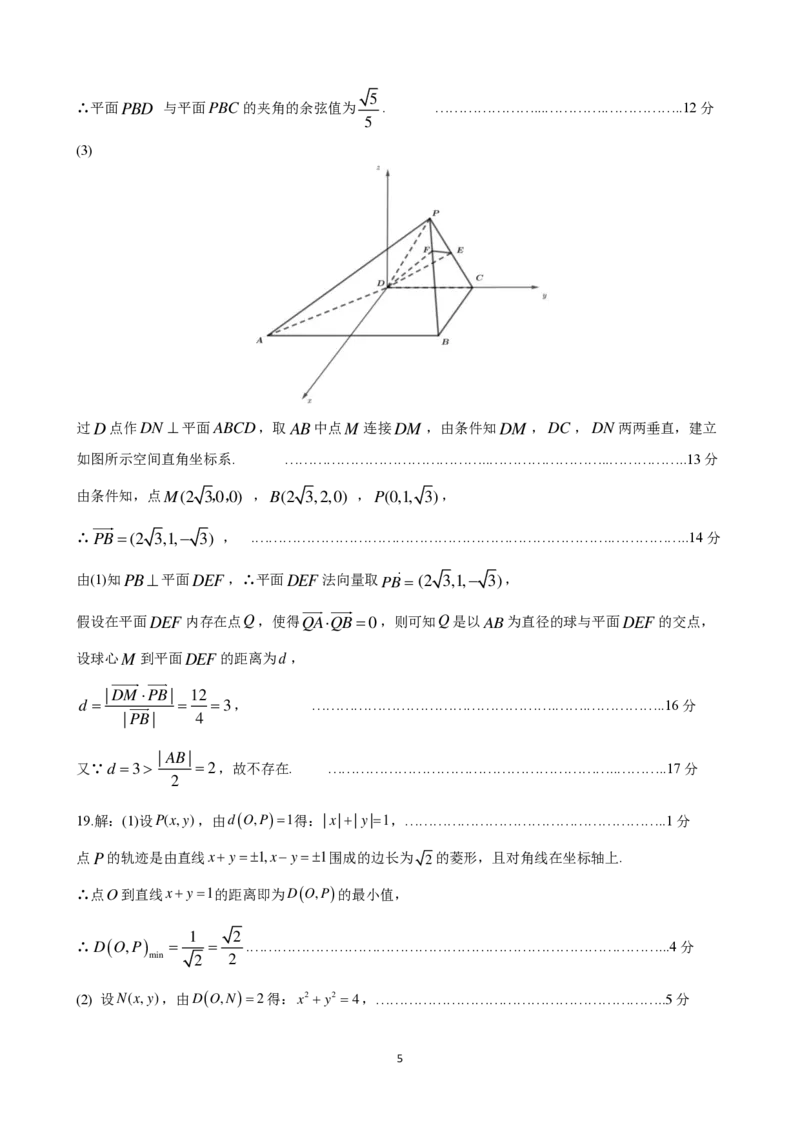…………………...………….……………..12分 (3) 过 D 点作 D N ⊥ 平面 A B C D ，取 A B 中点 M 连接DM ，由条件知 D M ， D C ， D N 两两垂直，建立 如图所示空间直角坐标系. ……………………………………..……………………..……………..13分 由条件知，点 M ( 2 3 ， 0 ， 0 ) ， B ( 2 3 , 2 , 0 ) ， P ( 0 , 1 , 3 ) ， ∴ P B = ( 2 3 , 1 , − 3 ) ， .………………………………………………………………….……………..14分 由(1)知 P B ⊥ 平面 D E F ，∴平面 D E F 法向量取 P B = ( 2 3 , 1 , − 3 ) ， 假设在平面 D E F 内存在点 Q ，使得 Q A  Q B = 0 ，则可知 Q 是以 A B 为直径的球与平面 D E F 的交点， 设球心 M 到平面 D E F 的距离为d ， d = | D M | P  B P | B | = 1 2 4 = 3 ， …………………………………………….…….……………..16分 | AB| 又∵d =3 =2，故不存在. ……………………………………………………..………..17分 2 19.解：(1)设 P ( x , y ) ，由d(O,P)=1得：|x|+|y|=1，………………………………………………..1分 点P的轨迹是由直线x+y=1,x−y=1围成的边长为 2的菱形，且对角线在坐标轴上. ∴点O到直线 x + y = 1 的距离即为D(O,P)的最小值， 1 2 ∴D(O,P) = = .……………………………………………………………………………...4分 min 2 2 (2) 设N(x,y)，由D(O,N)=2得：x2+y2 =4，……………………………………………………..5分令 6 x y 2 2 c s o s in , ,    = = ( R   )，  ∴d(M,N)=|3−x|+|2−y|=3−2cos+2−2sin=5−2 2sin(+ ). ………………..8分 4 ∵ R   ，∴d(M,N) =5+2 2. ……………………………………..9分 max (3)∵ g ( x ) = a l n x − x 过定点 ( 1 , − 1 ) ，当B为(1,−1)时， 1 1 此时d(A,B)= x −x + y − y = x −1+ − +1 =2+(−x )+(− )4， 1 2 1 2 1 x 1 x 1 1 即 A ( − 1 ,1 ) ， B ( 1 , − 1 ) 时满足 d ( A , B ) = 4 . ∵对于函数 h ( x 、) g ( x ) 图象上的点 A 、 B 有d(A,B)的最小值为4， ∴只需 d ( A , B )  4 ，求 a 的值即可. …………………………………………….…….……..10分 ∵ x 1  0 ， x 2  0 ，∴ x 1  x 2 ， ∴ d ( A , B ) = x 2 − x 1 + y 1 − y 2 ①当 y 1  y 2 时， d ( A , B ) = x 2 − x 1 + ( − 1 x 1 ) − ( a l n x 2 − x 2 ) = x 2 − x 1 + 1 x 1 + a ln x 2 − x 2 = a ln x 2 − x 1 + 1 x 1 ∵ l n x 2  R 1 ，(−x + )R， 1 x 1 ∴此时没有a能使d(A,B)4恒成立. ………………………………….…….……..11分 ②当 y 1  y 2 时， d ( A , B ) = x 2 − x 1 + ( − 1 x 1 ) − ( a l n x 2 − x 2 ) = x 2 − x 1 + ( − 1 x 1 ) − ( a l n x 2 − x 2 ) = 2 x 2 − a l n x 2 + ( − x 1 ) + ( − 1 x 1 )  2 x 2 − a l n x 2 + 2 ，当且仅当x =−1 时，上式等号成立. 1 要使d(A,B)4，则 2 x 2 − a ln x 2 + 2  4 ，即2x −alnx −20. ……….………….…..13分 2 2 构造函数(x)=2x−alnx−2(x0)，要使 d ( A , B )  4 ，即等价于求 a 取何值时(x)0恒成立. a 2x−a a ∵(x)=2− = ，令(x)=0，得x= (a0). x x 2∴ 7 x  ( 0 , a 2 ) 时， ( x ) 0    ， ( x )   在 ( 0 , a 2 ) 上单调递减； ∴ x  ( a 2 ， +  ) 时，(x)0， ( x )   在 ( a 2 ， +  ) 上单调递增. ∴ ( x ) m in ( a 2 ) a a l n a 2 2   = = − − ，要使(x)0恒成立，即 ( x ) m in a a l n a 2 2 0  = − −  . ……………………………………………………………………………………..……………….……..15分 构造函数 k ( x ) = x − x l n x 2 − 2 ( x  0 ) ， ∵ k  ( x ) = 1 − ( l n x 2 + 1 ) = − l n x 2 ，令 k ( x ) = − l n x 2 = 0 ，得 x = 2 ， ∴ x  ( 0 , 2 ) 时， k ( x )  0 ，∴ k ( x ) 在 x  ( 0 , 2 ) 上单调递增； ∴ x  ( 2 , +  ) 时， k ( x )  0 ，∴ k ( x ) 在x(2，+)上单调递减. ∴ k ( x ) m a x = k ( 2 ) = 0 ， 因此要使 ( x ) 0   恒成立，则a=2. ……………………………………………..……..17分 结合图象可知，当a=2时，也满足 x 1  x 2 , y 1  y 2 .因此， a = 2 .