文档内容
成都石室中学2024~2025学年度上期高2025届十一月月考
数学试卷
一、单项选择题:本题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合要
求的.
1. 已知集合 ,集合 ,则 ( )
A. B. C. D.
2. 已知 为单位圆 的内接正三角形,则 ( )
A. B. C. 1 D.
3. 已知角 的终边上一点 ,则 ( )
A. B. C. D.
4. 巴黎奥运会期间,旅客人数(万人)为随机变量 ,且 .记一天中旅客人数不少于26万
人的概率为 ,则 的值约为( )
(参考数据:若 ,有 , ,
)
A. 0.977 B. 0.9725 C. 0.954 D. 0.683
5.已知非零向量 , 满足 ,且向量 在向量 上的投影向量是 ,则 与 的夹角
是( )
A. B. C. D.
1
学科网(北京)股份有限公司6. 关于 的方程 在 上有( )个实数根.
A. 1 B. 2 C. 3 D. 4
7. 已知 , 是定义域为R的函数,且 是奇函数, 是偶函数,满足
,若对任意的 ,都有 成立,则实数a的取值
范围是( )
A. B. C.
D.
8. 已知 ,若关于 的不等式 在 上恒成立,则 的最小值
是( )
A. B. C. D.
二、多项选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.
全选对的得6分,部分选对的得部分分,有选错的得0分.
9. 已知函数 的部分图象如图所示,则下列说法正确的是(
)
A. 的图象关于直线 对称
B. 在 上单调递增
C. 是奇函数
2
学科网(北京)股份有限公司D. 将 图象上所有点的横坐标变为原来的2倍,得到函数 的图象
10. 已知 为函数 的一个零点,则( )
A. 的图象关于 对称 B. 的解集为
C. 时, D. 时, ,则 的最大值为4
11. 已知函数 与 及其导函数f'(x)与 的定义域均为 .若 为奇函数,
, ,则( )
A. B.
(1 )
C. 曲线y=f'(x)关于点 ,1 中心对称 D.
2
三、填空题:本大题共3小题,每小题5分,共计15分.
12. 若复数 满足 ,则 __________.
13. 已知某次数学期末试卷中有8道四选一的单选题,学生小万能完整做对其中 4道题,在剩下的4道题中,
有3道题有思路,还有1道完全没有思路,有思路的题做对的概率为 ,没有思路的题只能从4个选项中
随机选一个答案.若小万从这8个题中任选1题,则他做对的概率为______.
14. 已知数列{a }满足 , ,其中 为函数 的极值点,
n
则 ______.
四、解答题:共77分.解答应写出文字说明,证明过程或演算步骤.
15.(本小题13分)为提高学生的数学应用能力和创造力,石室中学打算开设“数学建模”选修课,为了
3
学科网(北京)股份有限公司解学生对“数学建模”的兴趣度是否与性别有关,学校随机抽取该校30名高中学生进行问卷调查,其中认
为感兴趣的人数占70%.
感兴趣 不感兴趣 合计
男
12
生
女
5
生
合
30
计
(1)根据所给数据,完成下面的2×2列联表,并根据列联表判断,依据小概率值α=0.15的独立性检验,分析
学生对“数学建模”选修课的兴趣度与性别是否有关?
(2)若感兴趣的女生中恰有4名是高三学生,现从感兴趣的女生中随机选出3名进行二次访谈,记选出高三
女生的人数为X,求X的分布列与数学期望
附: ,其中 .
0.02 0.00
0.15 0.10 0.05 0.010 0.001
5 5
2.70 5.02 7.87
2.072 3.841 6.635 10.828
6 4 9
16.(本小题15分)如图所示,在四棱锥 中, , , .
(1)若 平面 , ,证明:
(2)若 底面 , , ,二面角 的余弦值为 ,求 的长.
4
学科网(北京)股份有限公司17.(本小题15分)设 的内角 所对的边分别为 ,且
.
(1)求
(2)若 ,求 的周长;
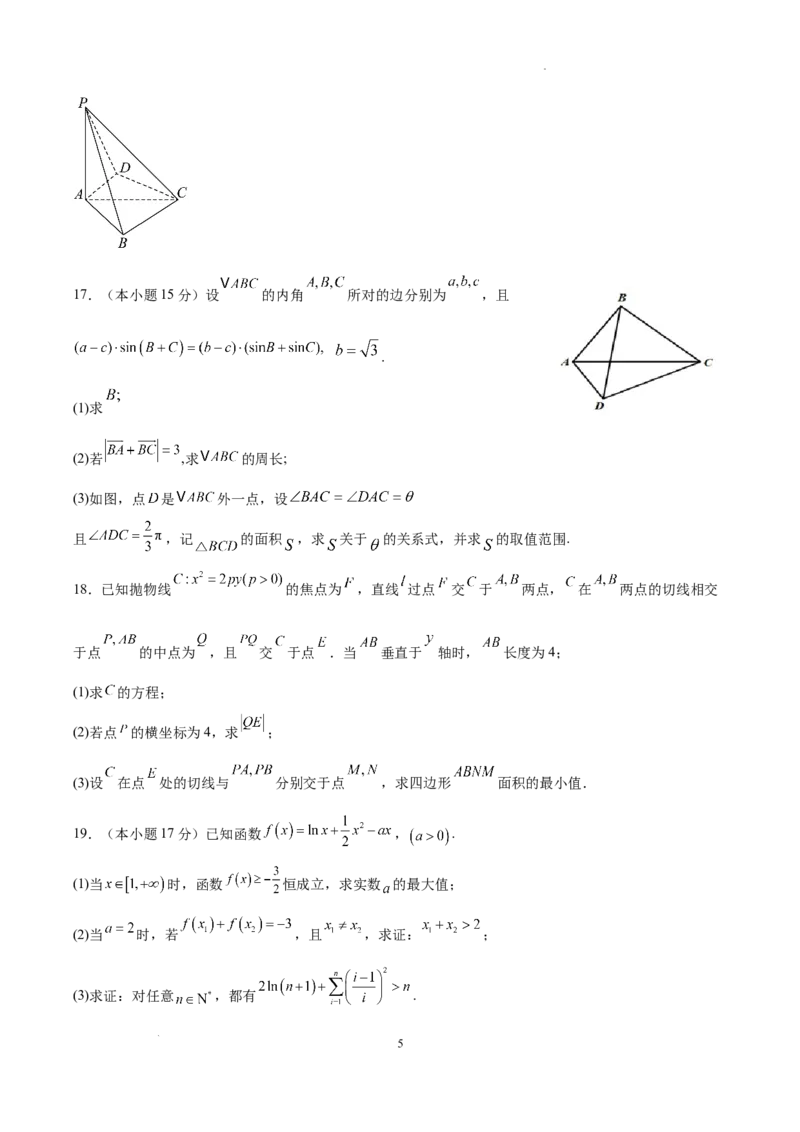
(3)如图,点 是 外一点,设
且 ,记 的面积 ,求 关于 的关系式,并求 的取值范围.
18.已知抛物线 的焦点为 ,直线 过点 交 于 两点, 在 两点的切线相交
于点 的中点为 ,且 交 于点 .当 垂直于 轴时, 长度为4;
(1)求 的方程;
(2)若点 的横坐标为4,求 ;
(3)设 在点 处的切线与 分别交于点 ,求四边形 面积的最小值.
19.(本小题17分)已知函数 , .
(1)当 时,函数 恒成立,求实数 的最大值;
(2)当 时,若 ,且 ,求证: ;
(3)求证:对任意 ,都有 .
5
学科网(北京)股份有限公司6
学科网(北京)股份有限公司