文档内容
2024 学年第一学期高二年级 10 月四校联考
数学 学科 试题卷
命题人:浦江中学
考生须知:
1.本卷满分 150分,考试时间 120分钟;
2.答题前,在答题卷指定区域填写班级、姓名、考场、座位号及准考证号(填涂);
3.所有答案必须写在答题卷上,写在试卷上无效;
一、选择题:本题共 8小题,每小题 5分,共 40分,在每小题给出的四个选项中,只有一项
是符合题目要求.
3x−3y−1=0
1. 直线 的倾斜角为( )
A. 30° B. 60° C. 120° D. 150°
2. 若圆锥的表面积为12π,底面圆的半径为2,则该圆锥的体积为( )
8 3
A. B. 4 3π C. π D. 8 3π
3
4√3
3 π
3. 设a∈R,则“a=1”是“直线l :ax+2y-1=0与直线l :x+(a+1)y+4=0平行”的( )
1 2
A. 充分不必要条件 B. 必要不充分条件
C. 充分必要条件 D. 既不充分也不必要条件
4. 在四面体OABC中,记OA=a,OB=b,OC =c,若点 M、N 分别为棱 OA、BC 的中点,则 MN =
( )
1 1 1 1 1 1
A. a+ b + c B. − a+ b + c
2 2 2 2 2 2
1 1 1 1 1 1
C. a− b + c D. a+ b − c
2 2 2 2 2 2
5. 直线x+ y+2=0分别与x轴, y轴交于A,B两点,点P在圆( x−2 )2 + y2 =2上,则ABP面积的取
第1页/共5页
学科网(北京)股份有限公司值范围是( )
A. [ 2,6 ] B. [ 4,8 ] C. 2,3 2 D. 2 2,3 2
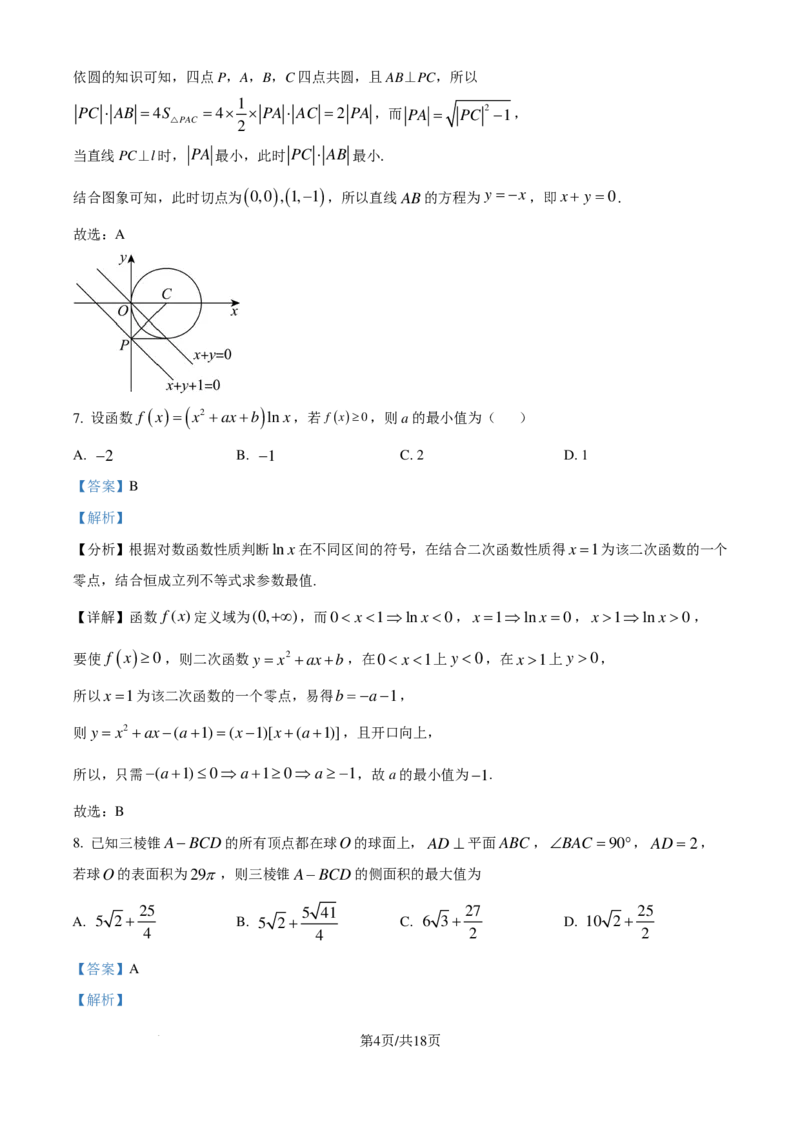
6. 已知圆C:x2 + y2 −2x=0,直线l:x+ y+1=0,P为l上的动点,过点P作圆C的两条切线PA、
PB,切点分别A、B,当 PC·AB 最小时,直线AB的方程为( )
A. x+ y =0 B. x− y =0
C. 2x−2y+1=0 D. 2x+2y+1=0
7. 设函数 f ( x )= ( x2 +ax+b ) lnx,若 f(x)≥0,则a的最小值为( )
A. −2 B. −1 C. 2 D. 1
8. 已知三棱锥A−BCD的所有顶点都在球O的球面上,AD ⊥平面ABC,∠BAC =90°,AD=2,
若球O的表面积为29π,则三棱锥A−BCD的侧面积的最大值为
25 5 41 27 25
A. 5 2+ B. 5 2+ C. 6 3+ D. 10 2+
4 4 2 2
二.多选题:本题共 3小题,每小题 6分,共 18分.在每小题给出的选项中,有多项符合题
目要求的,全部选对的得 6分,部分选对得部分分,有选错的得 0分.
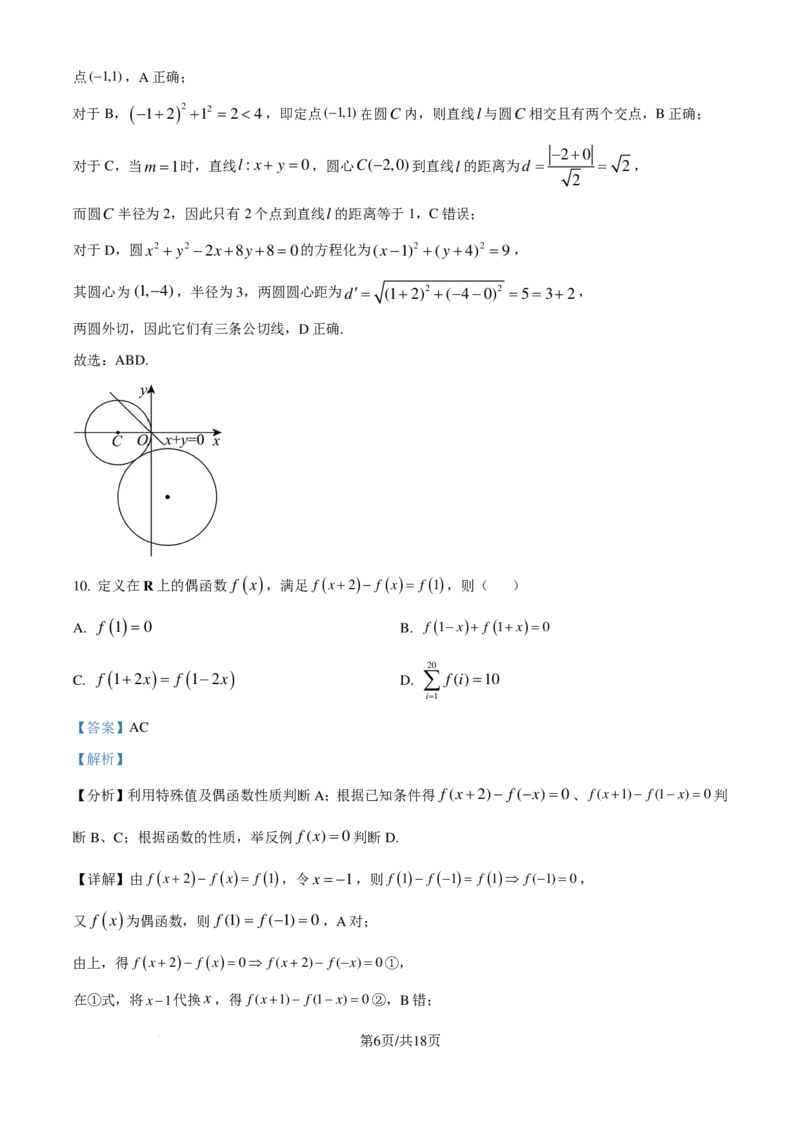
9. 已知圆C: ( x+2 )2 + y2 =4,直线l: ( m+1 ) x+2y−1+m=0 ( m∈R ) ,则( )
A. 直线l恒过定点
(−1,1 )
B. 直线l与圆C有两个交点
C. 当m=1时,圆C上恰有四个点到直线l的距离等于1
D. 圆C与圆x2 + y2 −2x+8y+8=0恰有三条公切线
10. 定义在R上的偶函数 f ( x ) ,满足 f (x+2)− f (x)= f (1),则( )
A. f ( 1 )=0 B. f (1−x)+ f (1+x)=0
20
C. f ( 1+2x )= f ( 1−2x ) D. ∑ f(i)=10
i=1
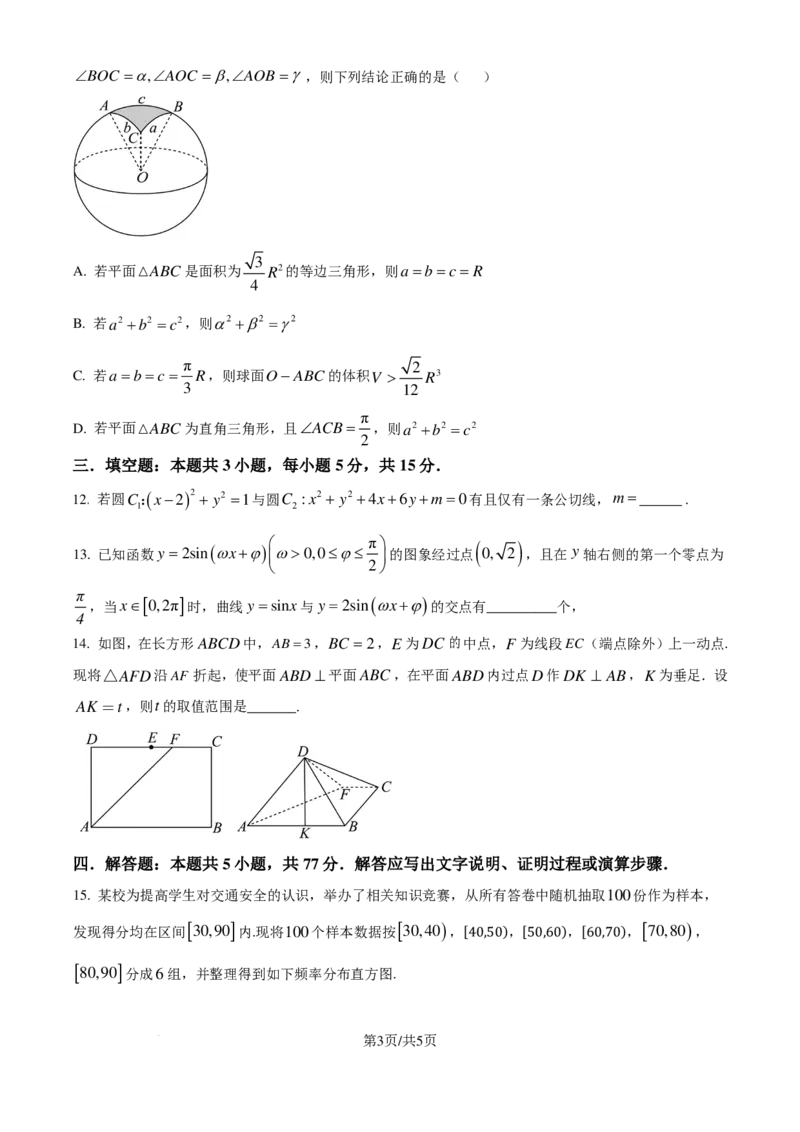
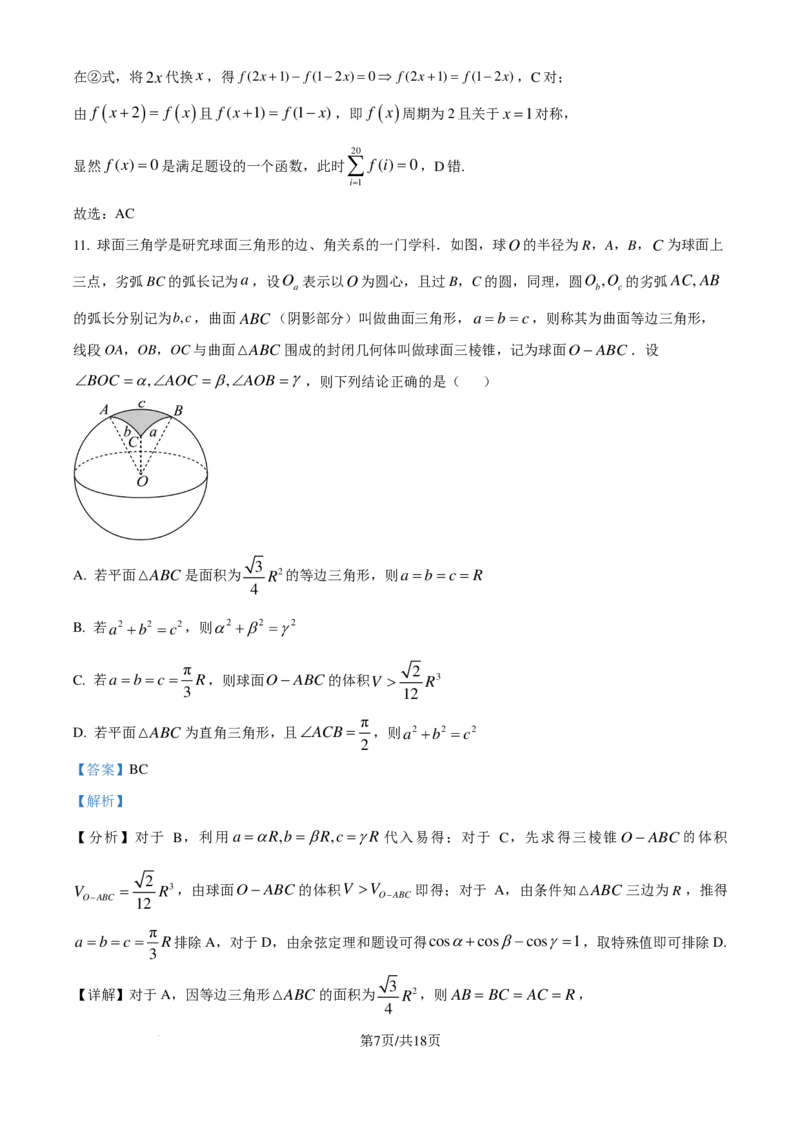
11. 球面三角学是研究球面三角形的边、角关系的一门学科.如图,球O的半径为R,A,B,C为球面上
三点,劣弧BC的弧长记为a,设O 表示以O为圆心,且过B,C的圆,同理,圆O ,O 的劣弧AC,AB
a b c
的弧长分别记为b,c,曲面ABC(阴影部分)叫做曲面三角形,a=b=c,则称其为曲面等边三角形,
线段OA,OB,OC与曲面ABC围成的封闭几何体叫做球面三棱锥,记为球面O− ABC.设
第2页/共5页
学科网(北京)股份有限公司∠BOC =α,∠AOC =β,∠AOB=γ ,则下列结论正确的是( )
3
A. 若平面ABC是面积为 R2的等边三角形,则a=b=c= R
4
B. 若a2 +b2 =c2,则α2 +β2 =γ2
π 2
C. 若a=b=c= R,则球面O− ABC的体积V > R3
3 12
π
D. 若平面ABC为直角三角形,且∠ACB = ,则a2 +b2 =c2
2
三.填空题:本题共 3小题,每小题 5分,共 15分.
12. 若圆C:( x−2 )2 + y2 =1与圆C :x2 + y2 +4x+6y+m=0有且仅有一条公切线,m= ______ .
1 2
π ( )
13. 已知函数y =2sin (ωx+ϕ) ω>0,0≤ϕ≤ 的图象经过点 0, 2 ,且在 y轴右侧的第一个零点为
2
π
,当x∈[ 0,2π ] 时,曲线y =sinx与y =2sin (ωx+ϕ) 的交点有__________个,
4
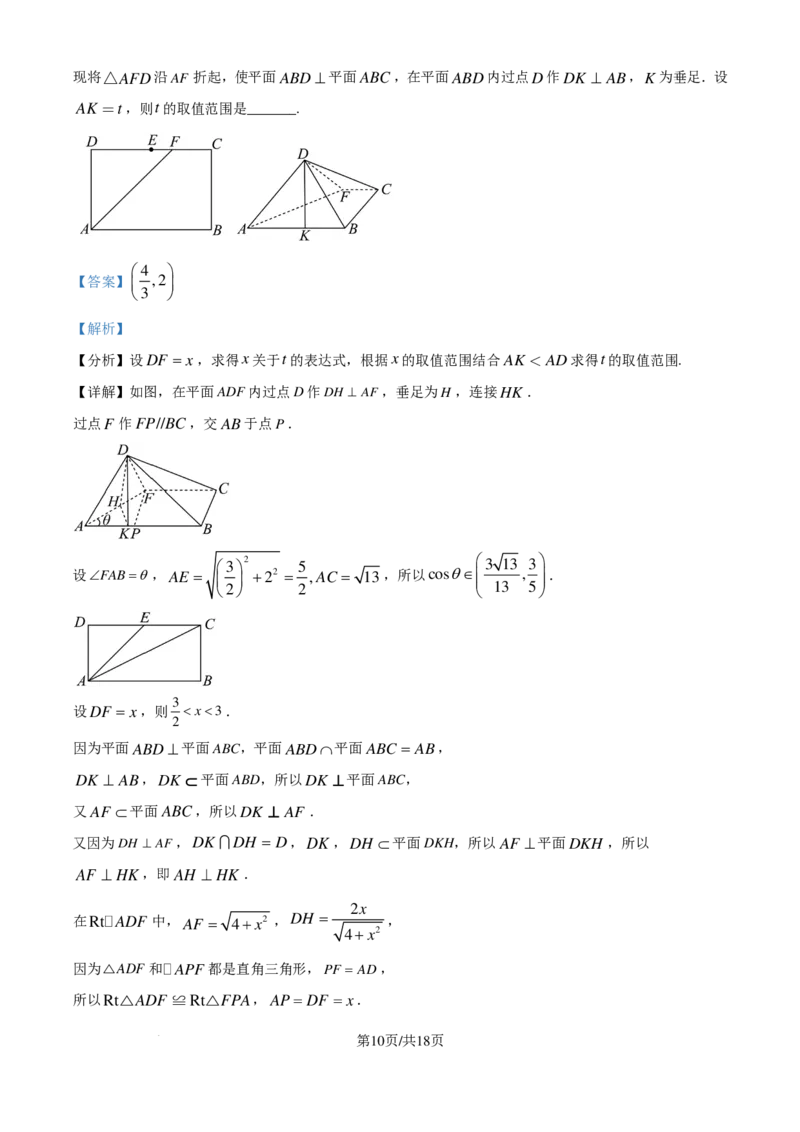
14. 如图,在长方形ABCD中,AB=3,BC =2,E为DC 的中点,F 为线段EC(端点除外)上一动点.
现将△AFD沿AF 折起,使平面ABD⊥平面ABC,在平面ABD内过点D作DK ⊥ AB,K为垂足.设
AK t,则t的取值范围是_______.
四.解答题:本题共 5小题,共 77分.解答应写出文字说明、证明过程或演算步骤.
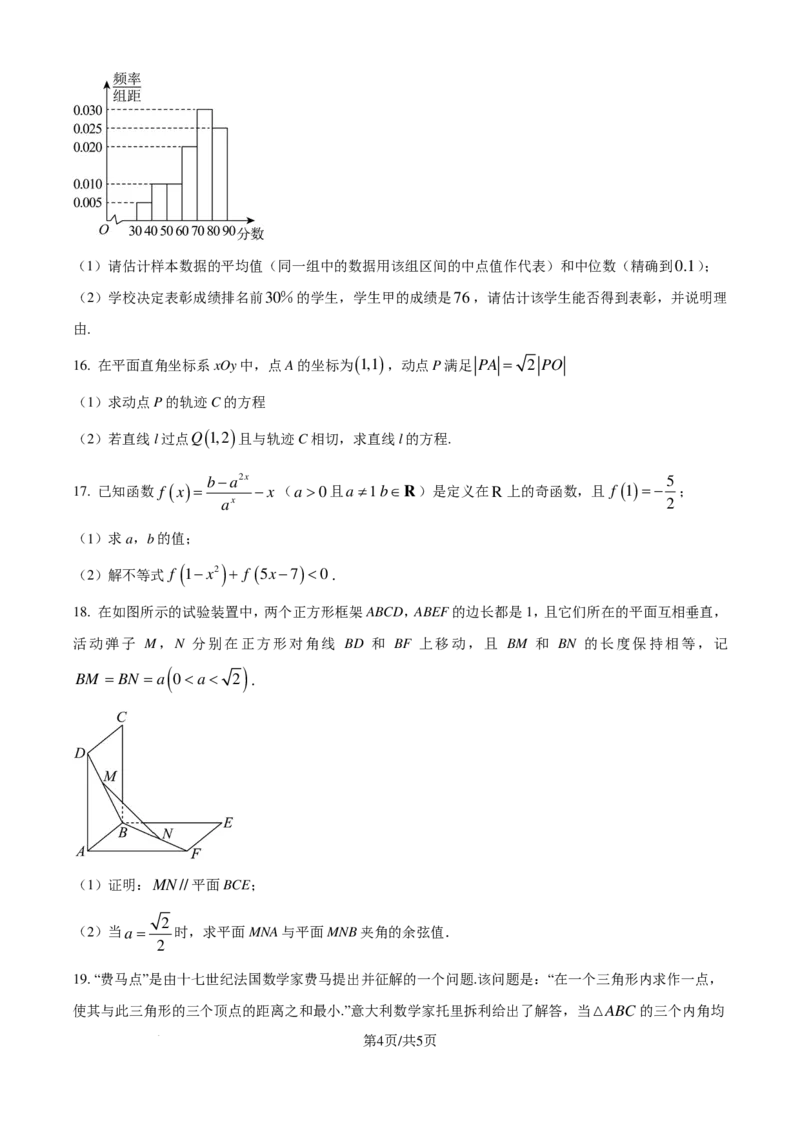
15. 某校为提高学生对交通安全的认识,举办了相关知识竞赛,从所有答卷中随机抽取100份作为样本,
[ ] [ ) [ )
发现得分均在区间 30,90 内.现将100个样本数据按 30,40 , , , , 70,80 ,
[40,50) [50,60) [60,70)
[ ]
80,90 分成6组,并整理得到如下频率分布直方图.
第3页/共5页
学科网(北京)股份有限公司(1)请估计样本数据的平均值(同一组中的数据用该组区间的中点值作代表)和中位数(精确到0.1);
(2)学校决定表彰成绩排名前30%的学生,学生甲的成绩是76,请估计该学生能否得到表彰,并说明理
由.
16. 在平面直角坐标系xOy中,点A的坐标为 ( 1,1 ) ,动点P满足 PA = 2 PO
(1)求动点P的轨迹C的方程
( )
(2)若直线l过点Q 1,2 且与轨迹C相切,求直线l的方程.
b−a2x 5
17. 已知函数 f ( x )= −x(a>0且a≠1b∈R)是定义在R 上的奇函数,且 f ( 1 )=− ;
ax 2
(1)求a,b的值;
(2)解不等式 f ( 1−x2 ) + f ( 5x−7 )<0.
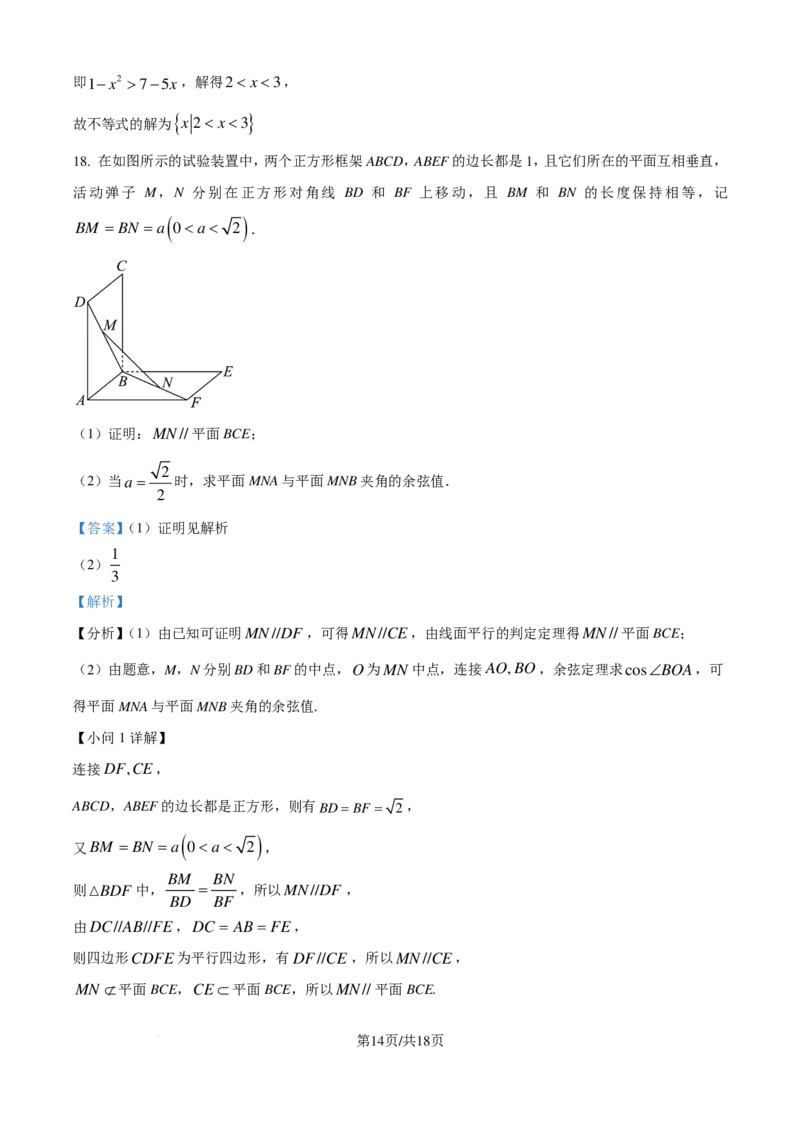
18. 在如图所示的试验装置中,两个正方形框架ABCD,ABEF的边长都是1,且它们所在的平面互相垂直,
活动弹子 M,N 分别在正方形对角线 BD 和 BF 上移动,且 BM 和 BN 的长度保持相等,记
( )
BM = BN =a 01⇒lnx>0,
要使 f ( x )≥0,则二次函数y = x2 +ax+b,在0< x<1上 y<0,在x>1上y >0,
所以x=1为该二次函数的一个零点,易得b=−a−1,
则y = x2 +ax−(a+1)=(x−1)[x+(a+1)],且开口向上,
所以,只需−(a+1)≤0⇒a+1≥0⇒a≥−1,故a的最小值为−1.
故选:B
8. 已知三棱锥A−BCD的所有顶点都在球O的球面上,AD ⊥平面ABC,∠BAC =90°,AD=2,
若球O的表面积为29π,则三棱锥A−BCD的侧面积的最大值为
25 5 41 27 25
A. 5 2+ B. 5 2+ C. 6 3+ D. 10 2+
4 4 2 2
【答案】A
【解析】
第4页/共18页
学科网(北京)股份有限公司【分析】由题意画出图形,设球O得半径为R,AB=x,AC=y,由球O的表面积为29π,可得x2+y2=25,写出
侧面积,再由基本不等式求最值.
【详解】设球O得半径为R,AB=x,AC=y,
由4πR2=29π,得4R2=29.又x2+y2+22=(2R)2,得x2+y2=25.三棱锥A-BCD的侧面积:
1 1 1 25 5 2
S=S +S +S = ⋅2x+ ⋅2y+ xy由x2+y2≥2xy,得 当且仅当x=y= 时取等号,由
ABD ACD ABC
2 2 2 2 2
△ △ △
xy≤
5 2 1 25
(x+y)2=x2+2xy+y2≤2(x2+y2),得 2 当且仅当x=y= 时取等号,∴ 2 ×
2 2 2
x+y≤5 , S≤5 + =
25 5 2 25
5 2+ 当且仅当x=y= 时取等号. ∴三棱锥A-BCD的侧面积的最大值为5 2+ .故选A.
4 2 4
【点睛】本题考查三棱锥的外接球、三棱锥的侧面积、基本不等式等基础知识,考查空间想象能力、逻辑
思维能力、运算求解能力,考查数学转化思想方法与数形结合的解题思想方法,是中档题.
二.多选题:本题共 3小题,每小题 6分,共 18分.在每小题给出的选项中,有多项符合题
目要求的,全部选对的得 6分,部分选对得部分分,有选错的得 0分.
9. 已知圆C: ( x+2 )2 + y2 =4,直线l: ( m+1 ) x+2y−1+m=0 ( m∈R ) ,则( )
A. 直线l恒过定点
(−1,1 )
B. 直线l与圆C有两个交点
C. 当m=1时,圆C上恰有四个点到直线l的距离等于1
D. 圆C与圆x2 + y2 −2x+8y+8=0恰有三条公切线
【答案】ABD
【解析】
【分析】求出直线l过的定点判断A;判断定点与圆的位置关系判断B;求出圆心到直线距离判断C;判断
圆与圆的位置关系判断D.
x+1=0 x=−1
【详解】对于A,直线l的方程为(x+1)m+ x+2y−1=0,由 ,得 ,直线l过定
x+2y−1=0 y =1
第5页/共18页
学科网(北京)股份有限公司点(−1,1),A正确;
对于B,(−1+2 )2 +12 =2<4,即定点(−1,1) 在圆C内,则直线l与圆C相交且有两个交点,B正确;
−2+0
对于C,当m=1时,直线l:x+ y =0,圆心C(−2,0)到直线l的距离为d = = 2,
2
而圆C半径为2,因此只有2个点到直线l的距离等于1,C错误;
对于D,圆x2 + y2 −2x+8y+8=0的方程化为(x−1)2 +(y+4)2 =9,
其圆心为 (1,−4),半径为3,两圆圆心距为d′= (1+2)2 +(−4−0)2 =5=3+2,
两圆外切,因此它们有三条公切线,D正确.
故选:ABD.
10. 定义在R上的偶函数 f ( x ) ,满足 f (x+2)− f (x)= f (1),则( )
A. f ( 1 )=0 B. f (1−x)+ f (1+x)=0
20
C. f ( 1+2x )= f ( 1−2x ) D. ∑ f(i)=10
i=1
【答案】AC
【解析】
【分析】利用特殊值及偶函数性质判断A;根据已知条件得 f(x+2)− f(−x)=0、f(x+1)− f(1−x)=0判
断B、C;根据函数的性质,举反例 f(x)=0判断D.
【详解】由 f (x+2)− f (x)= f (1),令x=−1,则 f (1)− f (−1)= f (1)⇒ f(−1)=0,
又 f ( x ) 为偶函数,则 f(1)= f(−1)=0,A对;
由上,得 f (x+2)− f (x)=0⇒ f(x+2)− f(−x)=0①,
在①式,将x−1代换x,得 f(x+1)− f(1−x)=0②,B错;
第6页/共18页
学科网(北京)股份有限公司在②式,将2x代换x,得 f(2x+1)− f(1−2x)=0⇒ f(2x+1)= f(1−2x),C对;
由 f ( x+2 )= f ( x ) 且 f(x+1)= f(1−x),即 f ( x ) 周期为2且关于x=1对称,
20
显然 f(x)=0是满足题设的一个函数,此时 ∑ f(i)=0,D错.
i=1
故选:AC
11. 球面三角学是研究球面三角形的边、角关系的一门学科.如图,球O的半径为R,A,B,C为球面上
三点,劣弧BC的弧长记为a,设O 表示以O为圆心,且过B,C的圆,同理,圆O ,O 的劣弧AC,AB
a b c
的弧长分别记为b,c,曲面ABC(阴影部分)叫做曲面三角形,a=b=c,则称其为曲面等边三角形,
线段OA,OB,OC与曲面ABC围成的封闭几何体叫做球面三棱锥,记为球面O−ABC.设
∠BOC =α,∠AOC =β,∠AOB=γ ,则下列结论正确的是( )
3
A. 若平面ABC是面积为 R2的等边三角形,则a=b=c= R
4
B. 若a2 +b2 =c2,则α2 +β2 =γ2
π 2
C. 若a=b=c= R,则球面O−ABC的体积V > R3
3 12
π
D. 若平面ABC为直角三角形,且∠ACB = ,则a2 +b2 =c2
2
【答案】BC
【解析】
【分析】对于 B,利用a =αR,b=βR,c=γR 代入易得;对于 C,先求得三棱锥O−ABC的体积
2
V = R3,由球面O−ABC的体积V >V 即得;对于 A,由条件知ABC 三边为R,推得
O−ABC
12
O−ABC
π
a=b=c= R排除A,对于D,由余弦定理和题设可得cosα+cosβ−cosγ=1,取特殊值即可排除D.
3
3
【详解】对于A,因等边三角形ABC的面积为 R2,则AB= BC = AC = R,
4
第7页/共18页
学科网(北京)股份有限公司π π
又OA=OB=OC = R,故α=β=γ = ,则a=b=c= R,故A错误;
3 3
对于B,由a2 +b2 =c2可得(αR)2 +(βR)2 =(γR)2,故α2 +β2 =γ2,即B正确;
π π
对于C,由a=b=c= R可得,α=β=γ= ,故AB= BC = AC = R.
3 3
1 R 3R
=
由正弦定理,ABC的外接圆半径为 2 π 3 ,点O到平面ABC的距离
sin
3
2
3R 6
h= R2 − = R,
3 3
1 1 3 6 2
则三棱锥O−ABC的体积V = S ⋅h= × R2× R= R3,
O−ABC
3
ABC
3 4 3 12
2
而球面O−ABC的体积V >V = R3,故C正确;
O−ABC
12
BC2 =2R2 −2R2cosα,
π
对于D,由余弦定理可知AC2 =2R2 −2R2cosβ,由C = 可得,BC2 + AC2 = AB2,
2
AB2 =2R2 −2R2cosγ,
即4R2 −2R2cosα−2R2cosβ=2R2 −2R2cosγ,化简得,cosα+cosβ−cosγ=1.
π π π π 2π2 π2
取α=β= ,γ= ,则a =b= R,c= R,则a2 +b2 = R2 < R2 =c2,故D错误.
3 2 3 2 9 4
故选:BC
三.填空题:本题共 3小题,每小题 5分,共 15分.
12. 若圆C:( x−2 )2 + y2 =1与圆C :x2 + y2 +4x+6y+m=0有且仅有一条公切线,m= ______ .
1 2
【答案】−23
【解析】
【分析】根据两圆的位置关系先确定两圆内切,再由圆心距计算即可.
【详解】由C :x2 + y2 +4x+6y+m=0⇒( x+2 )2 +( y+3 )2 =13−m,
2
显然13>m,C ( 2,0 ) ,C (−2,−3 ) ,
1 2
又C ,C 只有一条公切线,所以C ,C 相内切,
1 2 1 2
将C 点坐标代入圆C 方程知(−2−2 )2 +(−3 )2 >1,即C 在圆C 外部,
2 1 2 1
第8页/共18页
学科网(北京)股份有限公司所以圆C 内切于圆C ,
1 2
则有 CC = (−2−2 )2 +(−3−0 )2 =5= 13−m−1,
1 2
解之得m=−23.
故答案为:−23
π ( )
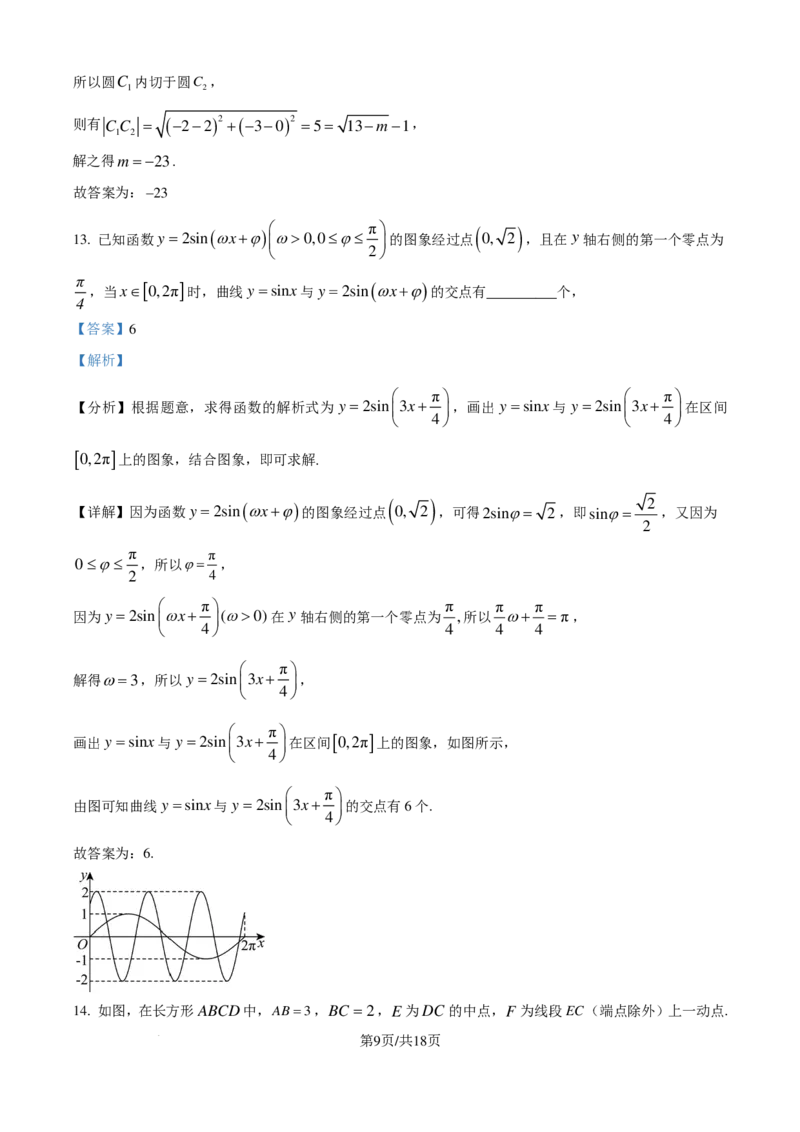
13. 已知函数y =2sin (ωx+ϕ) ω>0,0≤ϕ≤ 的图象经过点 0, 2 ,且在 y轴右侧的第一个零点为
2
π
,当x∈[ 0,2π ] 时,曲线y =sinx与y =2sin (ωx+ϕ) 的交点有__________个,
4
【答案】6
【解析】
π π
【分析】根据题意,求得函数的解析式为 y =2sin3x+ ,画出 y =sinx与 y =2sin3x+ 在区间
4 4
[ ]
0,2π 上的图象,结合图象,即可求解.
【详解】因为函数y =2sin (ωx+ϕ) 的图象经过点 ( 0, 2 ) ,可得2sinϕ= 2,即sinϕ= 2 ,又因为
2
π π
0≤ϕ≤ ,所以ϕ= ,
2 4
π π π π
因为y =2sin ωx+ (ω>0)在 y轴右侧的第一个零点为 ,所以 ω+ =π,
4 4 4 4
π
解得ω=3,所以y =2sin3x+ ,
4
π
画出y =sinx与y =2sin3x+ 在区间 [ 0,2π ] 上的图象,如图所示,
4
π
由图可知曲线y =sinx与y =2sin3x+ 的交点有6个.
4
故答案为:6.
14. 如图,在长方形ABCD中,AB=3,BC =2,E为DC 的中点,F 为线段EC(端点除外)上一动点.
第9页/共18页
学科网(北京)股份有限公司现将△AFD沿AF 折起,使平面ABD⊥平面ABC,在平面ABD内过点D作DK ⊥ AB,K为垂足.设
AK t,则t的取值范围是_______.
4
【答案】 ,2
3
【解析】
【分析】设DF = x,求得x关于t的表达式,根据x的取值范围结合AK AD求得t的取值范围.
【详解】如图,在平面ADF内过点D作DH ⊥ AF,垂足为H ,连接HK .
过点F 作FP//BC,交AB于点P.
3 2 5 3 13 3
设∠FAB=θ,AE = +22 = ,AC = 13,所以cosθ∈ , .
2 2 13 5
3
设DF = x,则 76,
0.30
所以估计学生甲不能得到表彰.
16. 在平面直角坐标系xOy中,点A的坐标为 ( 1,1 ) ,动点P满足 PA = 2 PO
(1)求动点P的轨迹C的方程
( )
(2)若直线l过点Q 1,2 且与轨迹C相切,求直线l的方程.
【答案】(1)x2 + y2 +2x+2y−2=0;
(2)x=1或5x−12y+19=0.
【解析】
【分析】(1)设P ( x,y ) ,根据动点P满足 PA = 2 PO ,再用两点间距离公式列式化简作答.
(2)讨论直线的斜率,设出直线l的方程,由圆心到直线的距离等于圆的半径求解作答.
【小问1详解】
设P ( x,y ) ,由|PA|= 2 |PO|,得 ( x−1 )2 +( y−1 )2 = 2⋅ x2 + y2 ,
化简得x2 + y2 +2x+2y−2=0,
所以P点的轨迹C的方程为x2 + y2 +2x+2y−2=0.
【小问2详解】
由(1)知,轨迹C:(x+1)2 +(y+1)2 =4表示圆心为C(−1,−1),半径为2的圆,
当直线l的斜率不存在时,方程为x=1,圆心C(−1,−1)到直线l的距离为2,l与C相切;
当直线l的斜率存在时,设l: y2kx1,即kx− y+2−k =0,
第12页/共18页
学科网(北京)股份有限公司|−2k+3|
5 5 19
于是 =2,解得k = ,因此直线l的方程为 x− y+ =0,即5x−12y+19=0,
k2 +1 12 12 12
所以直线l的方程为x=1或5x−12y+19=0.
b−a2x 5
17. 已知函数 f ( x )= −x(a>0且a≠1b∈R)是定义在R 上的奇函数,且 f ( 1 )=− ;
ax 2
(1)求a,b的值;
(2)解不等式 f ( 1−x2 ) + f ( 5x−7 )<0.
【答案】(1)b=1, a=2,
{ }
(2) x 2< x<3
【解析】
5
【分析】(1)根据 f ( 0 ) =0和 f ( 1 )=− 即可联立求解,
2
(2)根据函数的单调性以及奇偶性即可求解.
【小问1详解】
5
由题意可知: f ( 0 ) =0和 f ( 1 )=− ,
2
b−1 b−a2 5
故 f ( 0 )= −0=0且 f ( 1 )= −1=− ,
a0 a 2
1
故b=1, a=2,a =− (舍去)
2
【小问2详解】
1−22x 1
f ( x )= −x= −2x −x,
2x 2x
1
由于函数y = ,y =−2x,y =−x均为单调递减函数,故 f ( x ) 为单调递减,
2x
故 f ( 1−x2 ) + f ( 5x−7 )<0⇒ f ( 1−x2 ) < f ( 7−5x ) ,
第13页/共18页
学科网(北京)股份有限公司即1−x2 >7−5x,解得2< x<3,
{ }
故不等式的解为 x 2< x<3
18. 在如图所示的试验装置中,两个正方形框架ABCD,ABEF的边长都是1,且它们所在的平面互相垂直,
活动弹子 M,N 分别在正方形对角线 BD 和 BF 上移动,且 BM 和 BN 的长度保持相等,记
( )
BM = BN =a 0