文档内容
惠州中学2023级高二年级上学期期中考试
数学科试卷参考答案
说明:本试卷共4页,19小题,满分150分,考试用时120分钟。答案须做在答卷上;选择题填
涂须用2B铅笔,主观题须用黑色字迹的钢笔或签字笔作答。考试结束后只需交答卷。
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要
求的.
1.已知集合 , ,则下列结论正确的是( )
A={x|−1≤x≤1} B={x|x2−5x+6≥0}
A. A⊆B B. A∪B=A C. A∩B=B D. ∁ A=B
R
1.解: , ,
∵A={x|−1⩽x⩽1} B={x|x2−5x+6≥0}={x|x≥3或x≤2}
∴A⊆B,故A选项正确;∴A∪B={x|x≥3或x≤2}=B,故B选项错误;∴A∩B=A,故C选
项错误;
,故D选项错误.故选A.
∴∁ A={x|x<−1或x>1}≠B
R
2.复数z=−2i2−i+1,则z的虚部是( )
A. −i B. i C. −1 D. 1
2.解:复数z=−2i2−i+1=2−i+1=3−i,故z的虚部为−1.故选C.
{ x2+1,x≥2
3.已知函数f(x)= 则f(1)−f(3)= ( )
f(x+3),x<2,
A. −2 B. −7 C. 27
D. 7
{ x2+1,x≥2
3.解:f(x)= ,∴f(1)=f(1+3)=f(4)=17,f(3)=10,
f(x+3),x<2
则f(1)−f(3)=7,故选D.
4.已知 ( π) √3,则 ( π)的值是( )
cos x− =− cosx+cos x−
6 3 3
2√3 2√3
A. −1 B. ± C. − D. ±1
3 34.解:
π 1 √3 3 √3 √3 1 π
cosx+cos(x− )=cosx+ cosx+ sinx= cosx+ ⋅sinx=√3( cosx+ sinx)=√3cos(x− )=−1
3 2 2 2 2 2 2 6
故选A
5.已知空间向量 |⃗a|=3 , |⃗b|=2 ,且⃗
a⋅
⃗
b=2
,则 ⃗b 在⃗
a
上的投影向量为( )
2⃗ 9⃗ √6⃗
⃗
A. B. a C. a D. a
a
9 2 9
⃗ ⃗ ⃗ ⃗
a·b a 2 a 2⃗
5.解:由题意可知 ⃗b在 ⃗a上的投影向量为 = × = a,
|⃗| |⃗| 3 3 9
a a
2⃗
∴向量⃗b在向量⃗a上的投影向量为 a.故选B.
9
6.点A(4,−3),B(−2,−2),直线l过点P(1,1)且与线段AB相交,则直线l的斜率k的取值范围是(
)
4 4
A. k≥1或k≤−4 B. k≥1或k≤− C. −4≤k≤1 D. − ≤k≤1
3 3
6.解:如图,点A(4,−3),B(−2,−2),点P(1,1),
1+3 4 1+2
则k = =− ,k = =1,
PA 1−4 3 PB 1+2
直线l过点P(1,1),且与线段AB相交,
4
由图可知,k≥1或k≤− .故选B.
3
7.方程 所表示的图形是( )
|x|−1=√1−(y−1) 2
A. .一个半圆 B. 一个圆 C. 两个半圆 D. 两个圆
7.解:由题意,首先 ,平方整理得 ,
|x|>1 (|x|−1) 2+(y−1) 2=1
若x>1,则是以(1,1)为圆心,以1为半径的右半圆
若x<−1,则是以(−1,1)为圆心,以1为半径的左半圆
总之,方程表示的曲线是以(1,1)为圆心,以1为半径的右半圆与以(−1,1)为圆心,以1为半径的左半圆合
起来的图形 故选C.8.已知实数 满足 ,则|√3x+ y|的最大值为( )
x,y x2+(y−2) 2=1
2√x2+ y2
1 2√7 √3
A. B. C. 1 D.
2 7 2
|√3x+ y|
8解:设P(x,y)表示圆x2+(y−2) 2=1上一动点,则 表示点P到直线√3x+ y=0的距离d ,
2 1
|2|
√x2+ y2
表示点
P
到原点
O
的距离
d
,又圆心
(0,2)
到直线
√3x+ y=0
的距离为 =1,
2 √(√3) 2+12
所以直线 与圆 相切,记切点为 ( √3 3),
√3x+ y=0 x2+(y−2) 2=1 Q − ,
2 2
则|√3x+ y| = d 1=sin∠POQ⩽sin π = √3,当 P 点为(√3 , 3)取最大值. ∴ |√3x+ y| 的最大值为
2√x2+ y2 d 3 2 2 2 2√x2+ y2
2
√3
.故选D
2
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部
选对的得6分,部分选对的得2分,有选错的得0分.
9.已知向量 ⃗a=(2,−1,2) ,⃗
b=(2,2,1)
,⃗
c=(4,1,3)
,则( )
A. ⃗ ⃗ B. ⃗ ⃗
|a|=|b| c−b=(2,−1,2)
C. D. 向量 , , 共面
⃗a⊥⃗b ⃗a ⃗b ⃗c
9.解:因为 ⃗a=(2,−1,2) ,⃗
b=(2,2,1)
,
所以 ⃗ , ⃗ ,所以A正确;
|a|=√22+(−1) 2+22=3 |b|=√22+22+12=3
⃗ ⃗ ,故B正确;
c−b=(4,1,3)−(2,2,1)=(2,−1,2)⃗ ⃗ ,故C不正确;
a⋅b=2×2+(−1)×2+2×1=4≠0
由⃗
a+
⃗
b=(2,−1,2)+(2,2,1)=(4,1,3)
,所以
⃗c=⃗a+⃗b
,故选项D正确.故选:
ABD
.
10.已知直线l:y=kx+k+1,下列说法正确的是( )
A. 直线l过定点(1,−1)
B. 当k=1时,l关于x轴的对称直线为x+ y+2=0
C. 点P(3,−1)到直线l的最大距离为2√5
D. 直线l一定经过第四象限
10.BC解:对于A,由直线l:y=kx+k+1可化简为y−1=k(x+1),
所以直线l表示经过定点(−1,1)、斜率为k的直线,故A项错误;
对于B,当k=1时,直线l的方程为y=x+2,
用−y代换y得−y=x+2,整理得x+ y+2=0,即为直线l关于x轴对称的直线,故B项正确;
对于C,因为直线l经过定点M(−1,1),所以当直线MP⊥l时,点P(3,−1)到直线l的距离最大,
最大距离为 ,故C项正确;
|MP|=√(−1−3) 2+(1+1) 2=2√5
对于D,当k=1时,直线l:y=x+2经过一、二、三象限,不经过第四象限,故D项错误.
故选:BC.
11.已知圆 ,点 为 轴上一个动点,过点 作圆 的两条切线,切点分别为 , ,直
M:x2+(y−2) 2=1 P x P M A B
线AB与MP交于点C,则下列结论正确的是( )
A. 四边形PAMB周长的最小值为2+2√3 B. |AB|的最大值为2
8 √15 9
C. 若P(1,0),则三角形PAB的面积为 D. 若Q( ,0),则|CQ|的最大值为
5 4 4
11.解:
PA,PB均与圆M相切,|MA|=|MB|=1,PA⊥AM,PB⊥BM,则 .
|PA|=|PB|=√|PM| 2 −1
对于 ,四边形 周长为 ,
A PAMB l=|PA|+|PB|+|AM|+|BM|=2√|PM| 2 −1+2
因为点P为x轴上一个动点,所以|PM|的最小值即为点M到x轴的距离d=|2−0|=2,则|PM|⩾2,
所以 ,
l=2√|PM| 2 −1+2⩾2√4−1+2=2√3+2
即四边形PAMB周长的最小值为2+2√3,故A正确;
对于B,可知△PAM≌△PBM,则∠AMP=∠BMP,
所以PM⊥AB,所以|AB|=2|AC|,
由 S = 1 |PA|·|AM|= 1 |PM|·|AC| 可得 |AC|= |PA|·|AM| = √|PM| 2 −1 = √ 1− 1 ,
△PAM 2 2 |PM| |PM| |PM| 2
因为
|PM|⩾2
,所以0< 1
⩽
1 ,所以√3
⩽
√
1−
1
<1
,
|PM| 2 4 2 |PM| 2
√3
即 ⩽|AC|<1,所以√3⩽|AB|<2,故B错误;
2
对于 ,若 ,则 ,
C P(1,0) |PM|=√(1−0) 2+(0−2) 2=√5
由选项AB可得
|PA|=√|PM| 2 −1=2
,
|AC|=
√
1−
1
=
2√5,
|AB|=2|AC|=
4√5,
|PM| 2 5 5
所以|PC|=√|PA| 2 −|AC| 2= √ 4− 4 = 4√5 ,
5 5
1 8
所以S = |AB|·|PC|= ,故C正确;
△PAB 2 5
对于D,设P(a,0),由PA⊥AM,PB⊥BM可得,点P,A,M,B四点都在以PM为直径的圆上,
则该圆的圆心为(a ),半径为|PM| √a2+4,
,1 =
2 2 2
所以该圆的方程为(
x−
a) 2
+(y−1) 2=
a2+4,
2 4
即 ,与圆 : 作差可得直线 的方程为 ,
x2+ y2−ax−2y=0 M x2+(y−2) 2=1 AB ax−2y+3=0
易得直线 过定点 ( 3);
AB N 0,
2
又因为直线PM为2x+ay=2a,易得直线PM过定点M(0,2),
因为直线AB与MP交于点C且PM⊥AB,所以CM⊥CN,
即点C的轨迹为以MN为直径的圆(不包含点M),所以点 C 的轨迹方程为 x2+ ( y− 7) 2 = 1 (y≠2) ,其中圆心为 E ( 0, 7),半径为 r= 1,
4 16 4 4
若 (√15 ),则 √15 49 1 9,
Q ,0 |CQ|⩽|QE|+r= + + =
4 16 16 4 4
9
即|CQ|的最大值为 ,故D正确.故选ACD.
4
三、填空题:本题共3小题,每小题5分,共15分,14题第一空2分,第二空3分.
12.已知圆M经过点A(−2,0),B(0,4),C(0,0),则圆M的标准方程为_________________.
12.解:设圆 的方程为 ,
M (x−a) 2+(y−b) 2=r2
(−2−a) 2+b2=r2 a=−1
则 所以所求圆的标准方程为 .
{ a2+(4−b) 2=r2 ,解得{b=2, (x+1) 2+(y−2) 2=5
a2+b2=r2 r=√5
13.已知直线 经过点 ,且⃗ 是 的方向向量,则点 到 的距离为_______.
l A(2,3,1) n=(√2,0,√2) l P(4,3,2) l
→ →
13.解:
P
→
A=(−2,0,−1)
,故|
P
⃗
A|
=√5,cos⟨P → A, → n⟩=
→
PA·n
→
= −
√5
3
×
√2
2
=− 3
1
√
0
10 ,
|PA||n|
→ → 3√10 √10
设直线 PA与直线 l所成的角为 θ,则
cosθ=|cos|
= ,故 sinθ= ,
10 10
→ √10 √2 √2
∴点 P(4,3,2)到直线 l的距离为 |PA|sinθ=√5× = .故答案为 .
10 2 2
14.在平面直角坐标系中, , ,定义 为两点之间的“折线
P(x ,y ) Q(x ,y ) d(P,Q)=|x −x |+|y −y |
1 1 2 2 1 2 1 2
距离”.坐标原点O与直线2x+ y−2√5=0上一点的“折线距离”的最小值是 _______ ;圆x2+ y2=1
上一点与直线2x+ y−2√5=0上一点的“折线距离”的最小值是 _______ .14.解:如图,
该直线与两轴的交点分别为N(0,2√5),M(√5,0),设P(x,y)为直线上任意一点,
作PQ⊥x轴于Q,于是有|PQ|=2|QM|,所以d=|OQ|+|QP|≥|OQ|+|QM|=|OM|,
即当P与M重合时,d =|OM|=√5,
min
如图所示:设F为圆上任意一点,过P、F分别作x、y轴的垂线交于点R,延长FR交直线于点R',
将F看作定点,由问题1知P与F的最小“折线距离”为|FR'|,设F的纵坐标为m,
2√5−m m+2√1−m2
则d =|FR'| ,|FR'|= −√1−m2=√5− ,
min min 2 2
π √5sin(θ+φ)
显然只需要考虑m∈[0,1],设m=sinθ(θ∈[0, ]),则|FR'|=√5− ,
2 2
1 2 1 2
其中cosφ= ,sinφ= ,所以当sinθ= ,cosθ= 时,
√5 √5 √5 √5
√5 √5
d =|FR'| = .故答案为:√5; .
min min 2 2
四、解答题:本题共6小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.(本小题13分)
为了加深师生对党史的了解,激发广大师生知史爱党、爱国的热情,我校举办了“学党史、育文化”暨“喜
迎党的生日”党史知识竞赛,并将2000名师生的竞赛成绩(满分100分)整理成如图所示的频率直方图.
(1)求频率直方图中a的值以及师生竞赛成绩的中位数;
(2)从竞赛成绩在[80,90),[90,100]的师生中,采用分层抽样的方法抽取6人,再从抽取的6人中随机抽
取2人,求2人的成绩来自同一区间的概率.15.解:(1)因为10(0.01+0.01+a+0.04+a)=1......1分
所以a=0.02,......2分
因为共五组,前三组的频率和0.1+0.1+0.2=0.4<0.5,......3分
前四组的频率和0.1+0.1+0.2+0.4=0.8>0.5,所以中位数位于第四组。......4分
设中位数为x,则x∈[80,90),因为(x−80)×0.04=0.1,......5分
所以x=82.5;......6分
(2)因为第四组与第五组的频率之比为2:1,
故按照分层抽样第四组抽取人数为4人,记为a,b,c,d,......7分
第五组抽取人数为2人,记为e,f,......8分
从6人中选出2人, 共有(a,b),(a,c),(a,d),(a,e),(a,f ),(b,c),(b,d),(b,e),(b,f ),
(c,d),(c,e),(c,f ),(d,e),(d,f ),(e,f ),......9分
样本点个数共有N=15种,......10分
其中选出的2人来自同一组的是:(a,b),(a,c),(a,d),(b,c),(b,d),(c,d),(e,f ),样本点个数
有M=7种,......11分
M 7
p= =
N 15
......12分
7
答:选出的2人中来自同一组的概率为 . ......13分
15
16.(本小题15分)
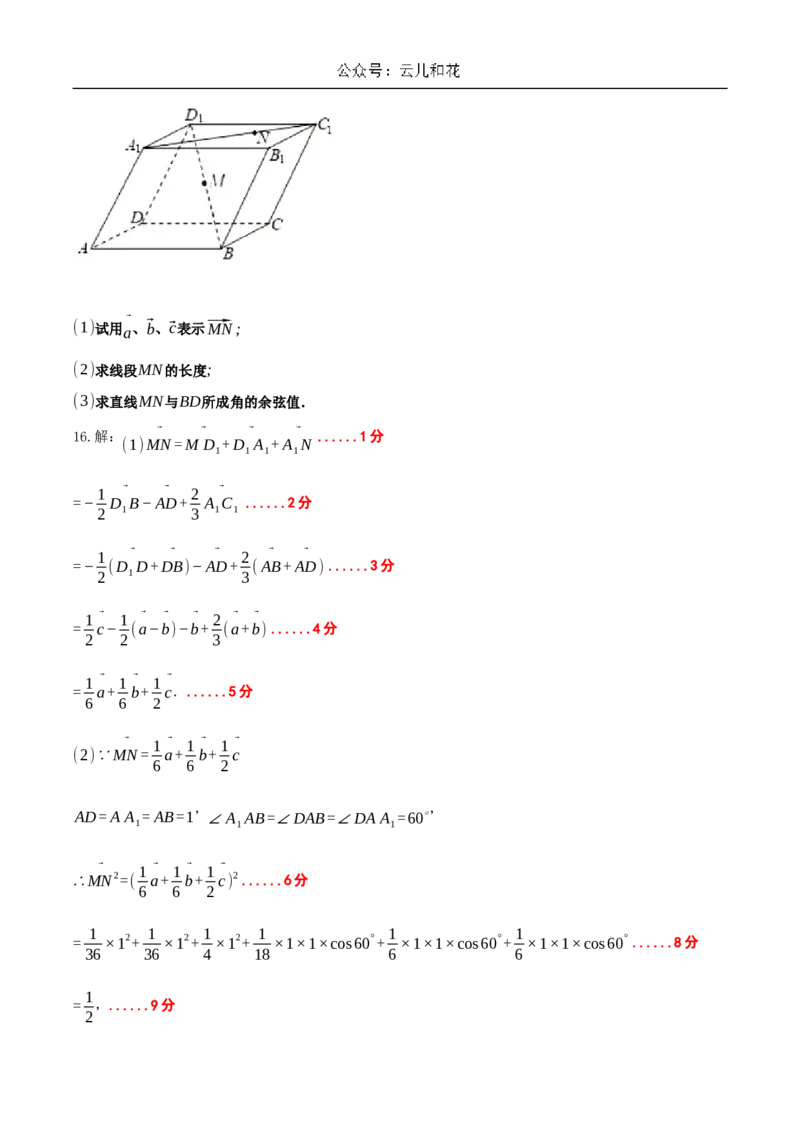
已知在平行六面体ABCD−A B C D 中,AD=A A =AB=1,∠A AB=∠DAB=∠DA A =60∘,
1 1 1 1 1 1 1
⃗ ⃗ ⃗ ⃗ ⃗ ⃗
A C =3NC ,D B=2MB,设⃗AB=⃗a,⃗AD=⃗b,A A =c;
1 1 1 1 1⃗
(1)试用 、⃗b、⃗c表示⃗MN;
a
(2)求线段MN的长度;
(3)求直线MN与BD所成角的余弦值.
16.解: ⃗ ⃗ ⃗ ⃗ ......1分
(1)MN=M D +D A +A N
1 1 1 1
1 ⃗ ⃗ 2 ⃗
=− D B−AD+ A C ......2分
2 1 3 1 1
1 ⃗ ⃗ ⃗ 2 ⃗ ⃗
=− (D D+DB)−AD+ (AB+AD) ......3分
2 1 3
1⃗ 1 ⃗ ⃗ ⃗ 2 ⃗ ⃗
= c− (a−b)−b+ (a+b) ......4分
2 2 3
1⃗ 1⃗ 1⃗
= a+ b+ c.......5分
6 6 2
⃗ 1⃗ 1⃗ 1⃗
(2)∵MN= a+ b+ c
6 6 2
, ,
AD=A A =AB=1 ∠A AB=∠DAB=∠DA A =60∘
1 1 1
⃗ 1⃗ 1⃗ 1⃗
∴MN2=( a+ b+ c) 2 ......6分
6 6 2
1 1 1 1 1 1
= ×12+ ×12+ ×12+ ×1×1×cos60°+ ×1×1×cos60°+ ×1×1×cos60° ......8分
36 36 4 18 6 6
1
= ,......9分
2√2
∴MN的长度为 .......10分
2
→ → → → →,......11分
(3)BD=AD−AB=b−a
⃗ ⃗ ⃗ ⃗ 1⃗ 1⃗ 1⃗
则MN⋅BD=(b−a)⋅( a+ b+ c) ......12分
6 6 2
1⃗ ⃗ 1⃗ 1⃗ ⃗ 1⃗ 1⃗ ⃗ 1⃗ ⃗
= b⋅a+ b2+ b⋅c− a2− a⋅b− a⋅c ......13分
6 6 2 6 6 2
=0 ......14分
∴直线MN与BD所成角的余弦值为0 ......15分
17.(本小题15分)
1
已知函数f(x)=√3sinxcosx− cos2x,
2
(1)求f(x)的最小正周期;
(2)在△ABC中,三个角A,B,C所对的边分别为a,b,c,若f(A)=1,c=2a⋅cosB、b=6,求
△ABC的面积.
1 √3 1
17.解:(1)∵函数f(x)=√3sinxcosx− cos2x= sin2x− cos2x ......1分
2 2 2
π
=sin(2x− ),......2分
6
2π
∴T= =π.......3分
2
∴f(x)的最小正周期π.......4分
(2)∵在△ABC中,三个角A,B,C所对的边分别为a,b,c,f(A)=1,
π
∴f(A)=sin(2A− )=1,......5分
6
π π π
∴2A− = +2kπ,kϵZ,∴A= +2kπ,kϵZ,......6分
6 2 3
π
∵0