文档内容
惠州中学 2023 级高二年级上学期期中考试
数学科试卷
说明:本试卷共4页,19小题,满分150分,考试用时120分钟。答案须做在答卷上;选择题填
涂须用2B铅笔,主观题须用黑色字迹的钢笔或签字笔作答。考试结束后只需交答卷。
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项
是符合题目要求的.
1.已知集合 , ,则下列结论正确的是( )
A={x|−1≤x≤1} B={x|x2−5x+6≥0}
A. A⊆B B. A∪B=A C. A∩B=B D. ∁ A=B
R
2.复数z=−2i2−i+1,则z的虚部是( )
A. −i B. i C. −1 D. 1
{ x2+1,x≥2
3.已知函数f(x)= 则f(1)−f(3)= ( )
f(x+3),x<2,
A. −2 B. −7 C. 27
D. 7
4.已知 ( π) √3,则 ( π) 的值是( )
cos x− =− cosx+cos x−
6 3 3
2√3 2√3
A. −1 B. ± C. −
3 3
D. ±1
5.已知空间向量 |⃗a|=3 , |⃗b|=2 ,且⃗
a⋅
⃗
b=2
,则 ⃗b 在⃗
a
上的投影向量为( )
2⃗ 9⃗ √6⃗
⃗
A. B. a C. a D. a
a
9 2 9
6.点A(4,−3),B(−2,−2),直线l过点P(1,1)且与线段AB相交,则直线l的斜率k的取值范围是
( )
4
A. k≥1或k≤−4 B. k≥1或k≤−
3
4
C. −4≤k≤1 D. − ≤k≤1
37.方程 所表示的图形是( )
|x|−1=√1−(y−1) 2
A. .一个半圆 B. 一个圆 C. 两个半圆
D. 两个圆
8.已知实数 满足 ,则|√3x+ y|的最大值为( )
x,y x2+(y−2) 2=1
2√x2+ y2
1 2√7 √3
A. B. C. 1 D.
2 7 2
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,
有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.已知向量 ⃗a=(2,−1,2) ,⃗
b=(2,2,1)
,⃗
c=(4,1,3)
,则( )
A. ⃗ ⃗ B. ⃗ ⃗
|a|=|b| c−b=(2,−1,2)
C. D. 向量 , , 共面
⃗a⊥⃗b ⃗a ⃗b ⃗c
10.已知直线l:y=kx+k+1,下列说法正确的是( )
A. 直线l过定点(1,−1)
B. 当k=1时,l关于x轴的对称直线为x+ y+2=0
C. 点P(3,−1)到直线l的最大距离为2√5
D. 直线l一定经过第四象限
11.已知圆 ,点 为 轴上一个动点,过点 作圆 的两条切线,切点分别为 ,
M:x2+(y−2) 2=1 P x P M A
B,直线AB与MP交于点C,则下列结论正确的是( )
A. 四边形PAMB周长的最小值为2+2√3
B. |AB|的最大值为2
8
C. 若P(1,0),则三角形PAB的面积为
5
√15 9
D. 若Q( ,0),则|CQ|的最大值为
4 4三、填空题:本题共3小题,每小题5分,共15分,14题第一空2分,第二空3分.
12.已知圆M经过点A(−2,0),B(0,4),C(0,0),则圆M的标准方程为 _____ _
.
13.已知直线 经过点 ,且⃗ 是 的方向向量,则点 到 的距离为
l A(2,3,1) n=(√2,0,√2) l P(4,3,2) l
_______.
14.在平面直角坐标系中, , ,定义 为两点之间的
P(x ,y ) Q(x ,y ) d(P,Q)=|x −x |+|y −y |
1 1 2 2 1 2 1 2
“折线距离”。坐标原点O与直线2x+ y−2√5=0上一点的“折线距离”的最小值
是 _______ ;圆x2+ y2=1上一点与直线2x+ y−2√5=0上一点的“折线距离”的最小值
是 _______ .
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.(本小题13分)
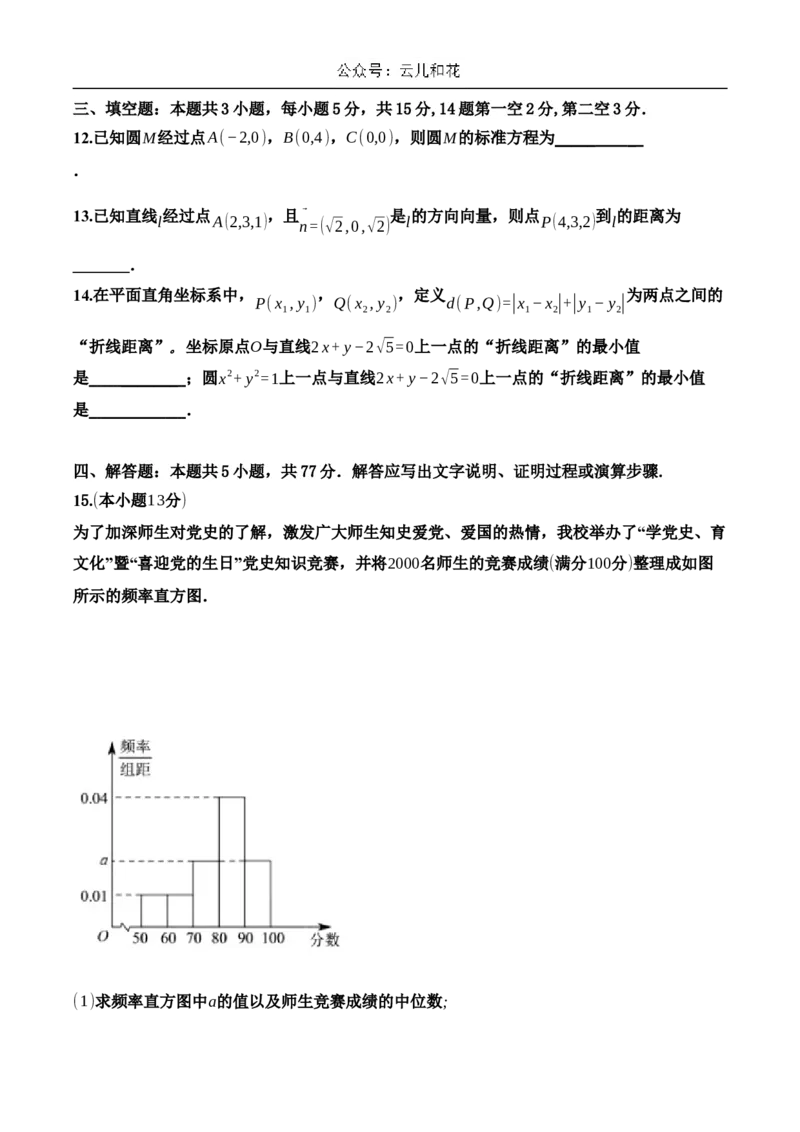
为了加深师生对党史的了解,激发广大师生知史爱党、爱国的热情,我校举办了“学党史、育
文化”暨“喜迎党的生日”党史知识竞赛,并将2000名师生的竞赛成绩(满分100分)整理成如图
所示的频率直方图.
(1)求频率直方图中a的值以及师生竞赛成绩的中位数;(2)从竞赛成绩在[80,90),[90,100]的师生中,采用分层抽样的方法抽取6人,再从抽取的6
人中随机抽取2人,求2人的成绩来自同一区间的概率.
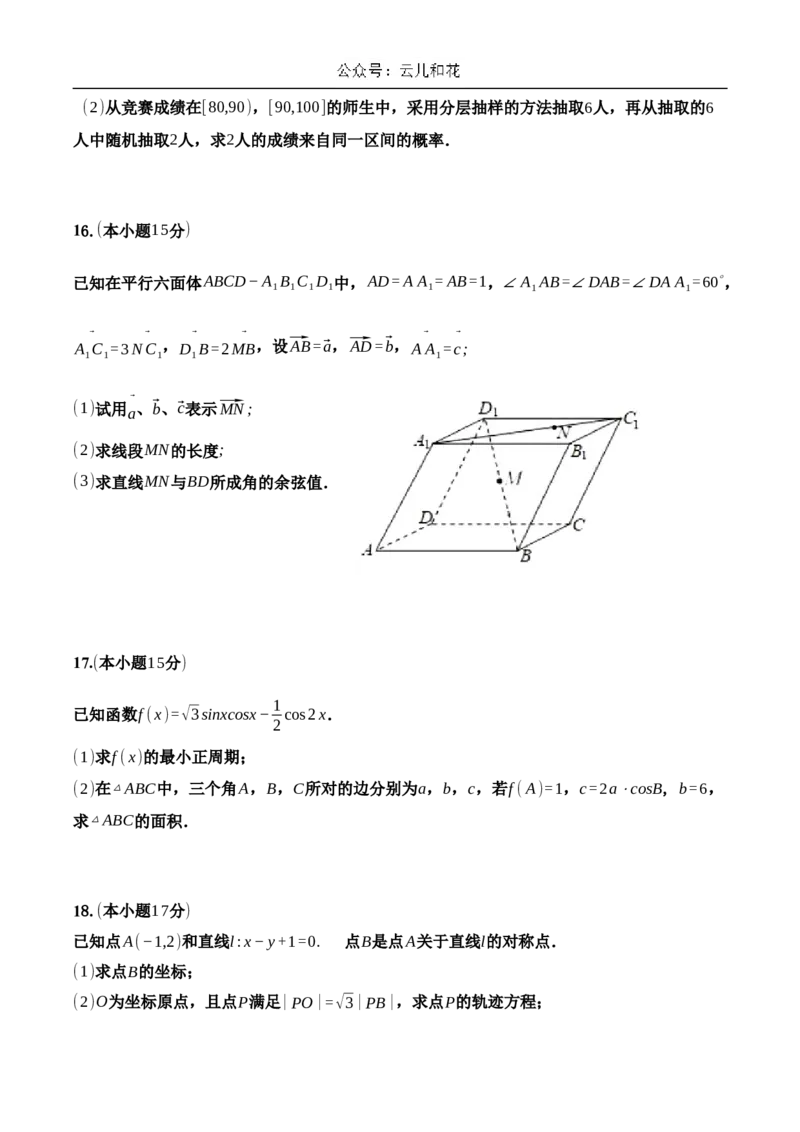
16.(本小题15分)
已知在平行六面体ABCD−A B C D 中,AD=A A =AB=1,∠A AB=∠DAB=∠DA A =60∘,
1 1 1 1 1 1 1
⃗ ⃗ ⃗ ⃗ ⃗ ⃗
A C =3NC ,D B=2MB,设⃗AB=⃗a,⃗AD=⃗b,A A =c;
1 1 1 1 1
⃗
(1)试用
a
、⃗b、⃗c表示⃗MN;
(2)求线段MN的长度;
(3)求直线MN与BD所成角的余弦值.
17.(本小题15分)
1
已知函数f(x)=√3sinxcosx− cos2x.
2
(1)求f(x)的最小正周期;
(2)在△ABC中,三个角A,B,C所对的边分别为a,b,c,若f(A)=1,c=2a⋅cosB, b=6,
求△ABC的面积.
18.(本小题17分)
已知点A(−1,2)和直线l:x−y+1=0. 点B是点A关于直线l的对称点.
(1)求点B的坐标;
(2)O为坐标原点,且点P满足|PO|=√3|PB|,求点P的轨迹方程;(3)若点P的轨迹与直线x+my+1=0有公共点,求m的取值范围.
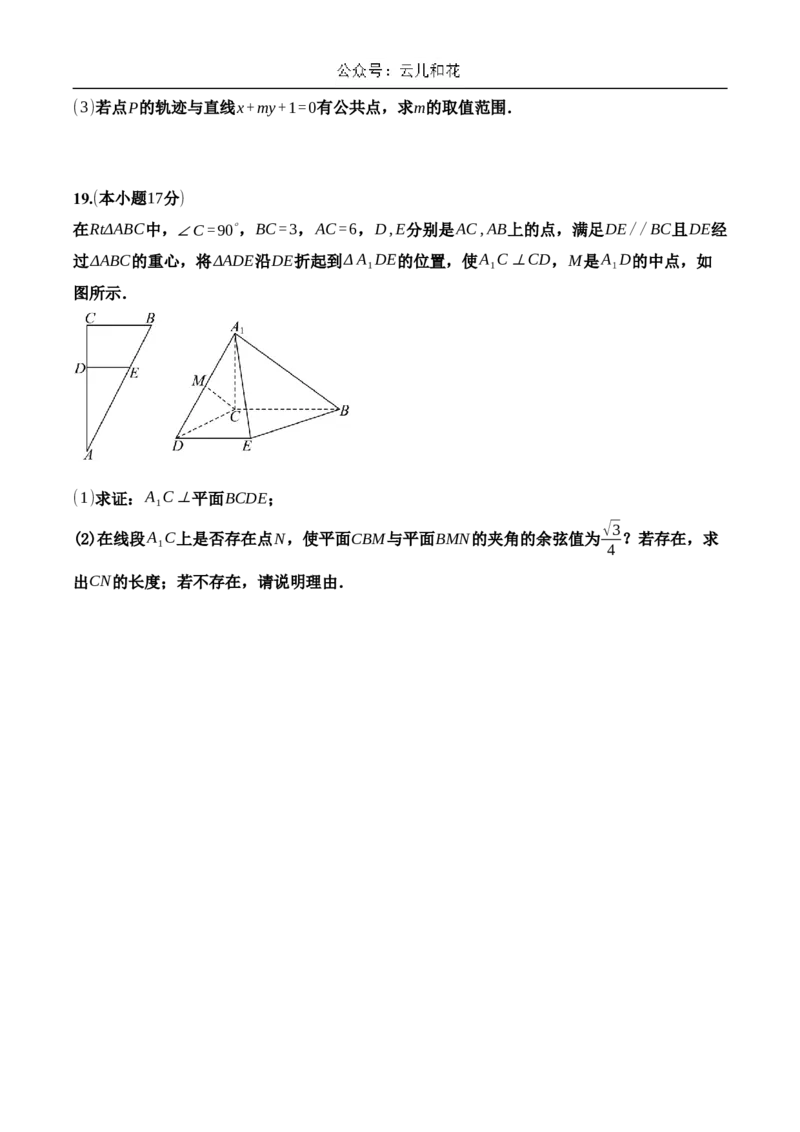
19.(本小题17分)
在RtΔABC中,∠C=90∘,BC=3,AC=6,D,E分别是AC,AB上的点,满足DE//BC且DE经
过ΔABC的重心,将ΔADE沿DE折起到ΔA DE的位置,使A C⊥CD,M是A D的中点,如
1 1 1
图所示.
(1)求证:A C⊥平面BCDE;
1
√3
(2)在线段A C上是否存在点N,使平面CBM与平面BMN的夹角的余弦值为 ?若存在,求
1 4
出CN的长度;若不存在,请说明理由.