2025—2026学年（上）高二级中段模块考试数学（答案）_251208广东省实验中学2025-2026学年高二上学期期中考试（全）

广东实验中学 2025—2026 学年（上）高二级期中考试 数学 答案及说明 题目 1 2 3 4 5 6 7 8 答案 C A B B A B D D 题目 9 10 11 12 13 14 y2 答案 ABC ABD ACD 3 x2   1 3 3 4 − 1．C 解：∵ 𝑧= 𝑖(2+𝑖)=2𝑖+𝑖2 =−1+2𝑖， ∴ 𝑧=−1−2𝑖，故选C． 3 3 3 2．A 解：由题意，直线可化为𝑦= 𝑥+ ，可得斜率𝑘= ， 3 3 3 3 设直线的倾斜角为𝛼，则tan𝛼= ，因为0°≤ 𝛼<180°，所以𝛼=30°．故选：A． 3 3．B  4．B 因为abcos2sin21cos210，[0,2)，所以  . 2 5．A 6．B 由题意，在正方体ABCD ABC D 中，可得AB //C D ， 1 1 1 1 1 1 1 1 所以直线C D 与平面ABC所成的角，即为AB 与平面ABC所成的角， 1 1 1 1 1 1 连接AB 交AB于点O，可得AB  AB， 1 1 1 1 又由BC⊥平面ABB A ，因为AB 平面ABB A ，可得BC  AB 1 1 1 1 1 1 由线面垂直判定定理，可得AB 平面ABC，所以B AO为AB 与平面ABC所成的角， 1 1 1 1 1 1 1 2 设正方体ABCD ABC D 的棱长为1，可得BO  , 1 1 1 1 1 2 BO 2 在直角  A 1 B 1 O中，sinB 1 A 1 O  A 1 B  2 ，因为B 1 A 1 O(0,90)，所以B 1 A 1 O  45. 1 1 x2 y2 x2 y2 7．D 设Ax,y ，Bx ,y ，则x x 2，y y 2，且 1  1 1， 2  2 1， 1 1 2 2 1 2 1 2 4 3 4 3 x2x2 y2y2 y y 3 x x 3 3 作差得 1 2  1 2 ，所以 1 2   1 2  ，即直线l的斜率是 ．故选：C． 4 3 x x 4 y y 4 4 1 2 1 2 8．D 由题意可知：圆𝑥2+𝑦2 =1的圆心为𝑂(0,0)，半径𝑟 =1， 1 圆(𝑥−5)2+(𝑦−2)= 4的圆心𝐴(5,2)，半径𝑟 =2， 2 则|𝑃𝑀|≥|𝑃𝑂|−1，|𝑃𝑁|≥ |𝑃𝐴|−2，即|𝑃𝑀|+|𝑃𝑁|≥|𝑃𝑂|+|𝑃𝐴|−3， 第 1 页 共 8 页𝑏−0 =1 设点𝑂(0,0)关于直线𝑥+𝑦+5= 0对称的点为𝐵(𝑎,𝑏)，则 𝑎−0 ，解得𝑎=𝑏 =−5，即𝐵(−5,−5)， 𝑎 𝑏 + +5=0 2 2 因为|𝑃𝑂|= |𝑃𝐵|，则|𝑃𝑀|+|𝑃𝑁|≥ |𝑃𝐵|+|𝑃𝐴|−3≥ |𝐴𝐵|−3= 149−3， 当且仅当𝐴，𝐵，𝑃三点共线时，等号成立，所以|𝑃𝑀|+|𝑃𝑁|的最小值为 149−3． 9．【答案】ABC 3𝑥+𝑦−9=0, 𝑥=3, 解：对于𝐴，当𝑎=3时，直线𝑙 :3𝑥+𝑦−9=0，直线𝑙 :2𝑥+2𝑦−6=0，由 解得 1 2 2𝑥+2𝑦−6= 0, 𝑦=0, 所以两直线的交点为(3,0)，故A正确; 𝑥−3= 0, 𝑥=3, 对于𝐵，直线𝑙 :(𝑥−3)𝑎+𝑦 =0，令 解得 即直线𝑙 恒过点(3,0)，故B正确; 1 𝑦=0, 𝑦=0, 1 1 对于𝐶:若𝑙 ⊥𝑙 ，则𝑎×2+1×(𝑎−1)= 0，解得𝑎= ，故C正确; 1 2 3 对于𝐷，假设存在𝑎∈𝑅，使𝑙 ∥𝑙 ，则𝑎×(𝑎−1)−2= 0，解得𝑎=2或𝑎=−1， 1 2 当𝑎=2时，𝑙 :2𝑥+𝑦−6=0，𝑙 :2𝑥+𝑦−6=0，两直线重合，舍去， 1 2 当𝑎=−1时，直线𝑙 :𝑥−𝑦−3=0，直线𝑙 :2𝑥−2𝑦−6= 0，两直线重合，舍去， 1 2 所以不存在𝑎∈ 𝑅，使𝑙 ∥𝑙 ，故D错误． 1 2 10．【答案】ABD 解：由椭圆方程知𝑎=3，𝑏=2，所以𝑐= 5，所以|𝑃𝐹 |+|𝑃𝐹 |= 6， 1 2 于是△𝑃𝐹 𝐹 的周长为2𝑎+2𝑐 =6+2 5，故A选项正确; 1 2 在△𝑃𝐹 𝐹 中，由余弦定理可得 1 2 |𝐹 𝐹 |2 =|𝑃𝐹 |2+|𝑃𝐹 |2−2|𝑃𝐹 ||𝑃𝐹 |cos∠𝐹 𝑃𝐹 1 2 1 2 1 2 1 2 =(|𝑃𝐹 |+|𝑃𝐹 |)2−2|𝑃𝐹 ||𝑃𝐹 |−2|𝑃𝐹 |⋅|𝑃𝐹 |cos∠𝐹 𝑃𝐹 ， 1 2 1 2 1 2 1 2 2 所以20=36−2|𝑃𝐹 |⋅|𝑃𝐹 |− |𝑃𝐹 ||𝑃𝐹 |，解得|𝑃𝐹 |𝑃𝐹 |= 6， 1 2 3 1 2 1 2 1 1 2 2 故𝑆 = |𝑃𝐹 ||𝑃𝐹 |sin∠𝐹 𝑃𝐹 = ×6× =2 2，故B选项正确; 𝛥𝑃𝐹1𝐹2 2 1 2 1 2 2 3 1 1 2 10 设点𝑃到𝑥轴的距离为𝑑，则𝑆 = |𝐹 𝐹 |⋅𝑑= ×2 5𝑑=2 2，所以𝑑= ，故C选项错误; 𝛥𝑃𝐹1𝐹2 2 1 2 2 5 (cid:4652)𝑃(cid:4652)(cid:4652)𝐹(cid:4652)(cid:4652)⃗⋅(cid:4652)𝑃(cid:4652)(cid:4652)𝐹(cid:4652)(cid:4652)⃗=|(cid:4652)𝑃(cid:4652)(cid:4652)𝐹(cid:4652)(cid:4652)⃗|⋅|𝑃(cid:4652)(cid:4652)(cid:4652)𝐹(cid:4652)(cid:4652)⃗|cos∠𝐹 𝑃𝐹 =6× 1 =2，故D选项正确． 1 2 1 2 1 2 3 第 2 页 共 8 页11．【答案】ACD 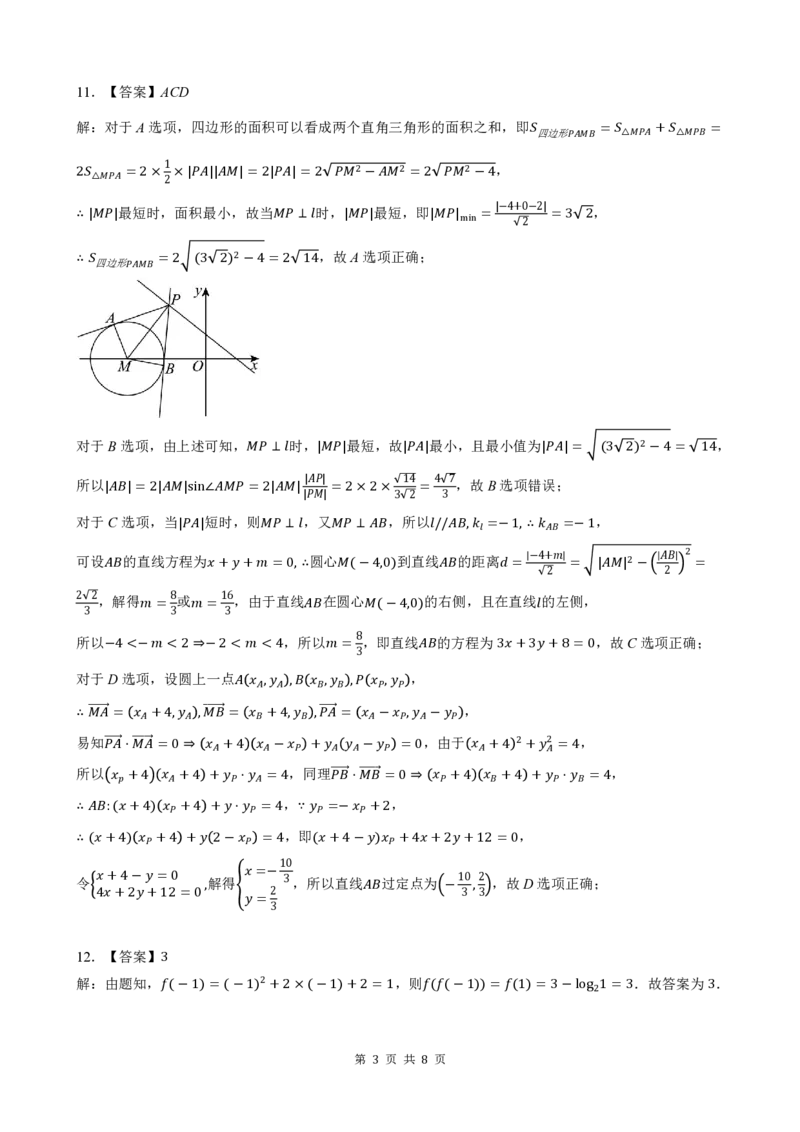解：对于A选项，四边形的面积可以看成两个直角三角形的面积之和，即𝑆 =𝑆 +𝑆 = 四边形𝑃𝐴𝑀𝐵 △𝑀𝑃𝐴 △𝑀𝑃𝐵 1 2𝑆 =2× ×|𝑃𝐴||𝐴𝑀|= 2|𝑃𝐴|= 2 𝑃𝑀2−𝐴𝑀2 =2 𝑃𝑀2−4， △𝑀𝑃𝐴 2 |−4+0−2| ∴|𝑀𝑃|最短时，面积最小，故当𝑀𝑃⊥ 𝑙时，|𝑀𝑃|最短，即|𝑀𝑃| = =3 2， min 2 ∴ 𝑆 =2 (3 2)2−4=2 14，故A选项正确； 四边形𝑃𝐴𝑀𝐵 对于B选项，由上述可知，𝑀𝑃⊥ 𝑙时，|𝑀𝑃|最短，故|𝑃𝐴|最小，且最小值为|𝑃𝐴|= (3 2)2−4= 14， |𝐴𝑃| 14 4 7 所以|𝐴𝐵|= 2|𝐴𝑀|sin∠𝐴𝑀𝑃=2|𝐴𝑀| =2×2× = ，故B选项错误； |𝑃𝑀| 3 2 3 对于C 选项，当|𝑃𝐴|短时，则𝑀𝑃⊥ 𝑙，又𝑀𝑃⊥ 𝐴𝐵，所以𝑙//𝐴𝐵,𝑘 =−1, ∴𝑘 =−1， 𝑙 𝐴𝐵 −4+𝑚 𝐴𝐵 2 可设𝐴𝐵的直线方程为𝑥+𝑦+𝑚=0, ∴圆心𝑀(−4,0)到直线𝐴𝐵的距离𝑑= = |𝐴𝑀|2− = 2 2 2 2 8 16 ，解得𝑚= 或𝑚 = ，由于直线𝐴𝐵在圆心𝑀(−4,0)的右侧，且在直线𝑙的左侧， 3 3 3 8 所以−4<−𝑚<2 ⇒−2< 𝑚<4，所以𝑚= ，即直线𝐴𝐵的方程为3𝑥+3𝑦+8=0，故C选项正确； 3 对于D选项，设圆上一点𝐴 𝑥 ,𝑦 ,𝐵 𝑥 ,𝑦 ,𝑃 𝑥 ,𝑦 ， 𝐴 𝐴 𝐵 𝐵 𝑃 𝑃 ∴ 𝑀(cid:4652)(cid:4652)(cid:4652)(cid:4652)𝐴⃗= 𝑥 +4,𝑦 ,𝑀(cid:4652)(cid:4652)(cid:4652)𝐵(cid:4652)⃗= 𝑥 +4,𝑦 ,𝑃(cid:4652)(cid:4652)(cid:4652)𝐴(cid:4652)⃗= 𝑥 −𝑥 ,𝑦 −𝑦 ， 𝐴 𝐴 𝐵 𝐵 𝐴 𝑃 𝐴 𝑃 易知(cid:4652)𝑃(cid:4652)(cid:4652)𝐴(cid:4652)⃗⋅𝑀(cid:4652)(cid:4652)(cid:4652)𝐴(cid:4652)⃗=0 ⇒ 𝑥 +4 𝑥 −𝑥 +𝑦 𝑦 −𝑦 =0，由于 𝑥 +4 2+𝑦2 =4， 𝐴 𝐴 𝑃 𝐴 𝐴 𝑃 𝐴 𝐴 所以 𝑥 +4 𝑥 +4 +𝑦 ⋅𝑦 =4，同理𝑃(cid:4652)(cid:4652)(cid:4652)𝐵(cid:4652)⃗⋅𝑀(cid:4652)(cid:4652)(cid:4652)𝐵(cid:4652)⃗=0 ⇒ 𝑥 +4 𝑥 +4 +𝑦 ⋅𝑦 =4， 𝑝 𝐴 𝑃 𝐴 𝑃 𝐵 𝑃 𝐵 ∴ 𝐴𝐵:(𝑥+4) 𝑥 +4 +𝑦⋅𝑦 =4，∵𝑦 =−𝑥 +2， 𝑃 𝑃 𝑃 𝑃 ∴(𝑥+4) 𝑥 +4 +𝑦 2−𝑥 =4，即(𝑥+4−𝑦)𝑥 +4𝑥+2𝑦+12=0， 𝑃 𝑃 𝑃 10 𝑥=− 令 𝑥+4−𝑦=0 ,解得 3，所以直线𝐴𝐵过定点为 − 10 , 2 ，故D选项正确； 4𝑥+2𝑦+12= 0 2 3 3 𝑦= 3 12．【答案】3 解：由题知，𝑓(−1)=(−1)2+2×(−1)+2= 1，则𝑓(𝑓(−1))= 𝑓(1)= 3−log 1=3．故答案为3． 2 第 3 页 共 8 页    4n 1 m 1 y2   13．【答案】 x2   1 解：由题意，设椭圆的方程为mx2  ny2  1，则 m ，解得 1 ． 4   3n  1 n    4 4 y2 ∴椭圆的标准方程为 x2   1 ． 4 14．【答案】 3 3 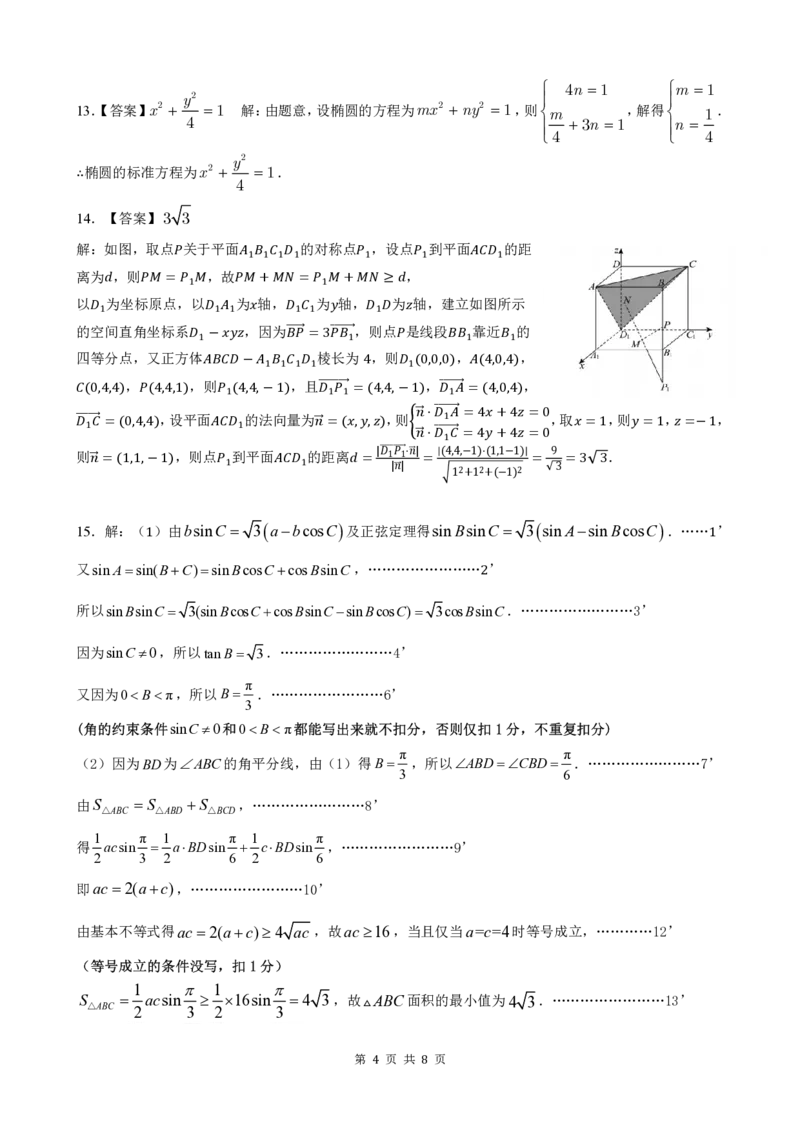解：如图，取点𝑃关于平面𝐴 𝐵 𝐶 𝐷 的对称点𝑃 ，设点𝑃 到平面𝐴𝐶𝐷 的距 1 1 1 1 1 1 1 离为𝑑，则𝑃𝑀=𝑃 𝑀，故𝑃𝑀+𝑀𝑁=𝑃 𝑀+𝑀𝑁≥ 𝑑， 1 1 以𝐷 为坐标原点，以𝐷 𝐴 为𝑥轴，𝐷 𝐶 为𝑦轴，𝐷 𝐷为𝑧轴，建立如图所示 1 1 1 1 1 1 的空间直角坐标系𝐷 −𝑥𝑦𝑧，因为𝐵(cid:4652)(cid:4652)(cid:4652)𝑃(cid:4652)⃗=3𝑃(cid:4652)(cid:4652)(cid:4652)𝐵(cid:4652)(cid:4652)⃗，则点𝑃是线段𝐵𝐵 靠近𝐵 的 1 1 1 1 四等分点，又正方体𝐴𝐵𝐶𝐷−𝐴 𝐵 𝐶 𝐷 棱长为4，则𝐷 (0,0,0)，𝐴(4,0,4)， 1 1 1 1 1 𝐶(0,4,4)，𝑃(4,4,1)，则𝑃 (4,4,−1)，且𝐷(cid:4652)(cid:4652)(cid:4652)(cid:4652)𝑃(cid:4652)(cid:4652)(cid:4652)⃗=(4,4,−1)，𝐷(cid:4652)(cid:4652)(cid:4652)(cid:4652)(cid:4652)𝐴⃗=(4,0,4)， 1 1 1 1 (cid:4652)𝑛⃗⋅𝐷(cid:4652)(cid:4652)(cid:4652)(cid:4652)(cid:4652)𝐴⃗=4𝑥+4𝑧=0 (cid:4652)𝐷(cid:4652)(cid:4652)(cid:4652)(cid:4652)𝐶⃗=(0,4,4)，设平面𝐴𝐶𝐷 的法向量为(cid:4652)𝑛⃗=(𝑥,𝑦,𝑧)，则 1 ，取𝑥=1，则𝑦=1，𝑧=−1， 1 1 (cid:4652)𝑛⃗⋅𝐷(cid:4652)(cid:4652)(cid:4652)(cid:4652)(cid:4652)𝐶⃗=4𝑦+4𝑧=0 1 则(cid:4652)𝑛⃗=(1,1,−1)，则点𝑃 到平面𝐴𝐶𝐷 的距离𝑑= |𝐷(cid:4652)(cid:4652)(cid:4652) 1 (cid:4652)(cid:4652)𝑃(cid:4652)(cid:4652)(cid:4652)(cid:4652) 1 ⃗⋅(cid:4652)𝑛⃗| = (4,4,−1)⋅(1,1−1) = 9 =3 3． 1 1 |(cid:4652)𝑛⃗| 3 12+12+(−1)2 15．解：（1）由bsinC  3abcosC及正弦定理得sinBsinC  3sinAsinBcosC．……1’ 又sinAsin(BC)sinBcosCcosBsinC ，……………………2’ 所以sinBsinC 3(sinBcosCcosBsinCsinBcosC) 3cosBsinC．……………………3’ 因为sinC0，所以tanB 3．……………………4’ π 又因为0Bπ，所以B ．……………………6’ 3 (角的约束条件sinC0和0Bπ都能写出来就不扣分，否则仅扣1分，不重复扣分) π π （2）因为BD为ABC的角平分线，由（1）得B ，所以ABDCBD ．……………………7’ 3 6 由S  S S ，……………………8’ △ABC △ABD △BCD 1 π 1 π 1 π 得 acsin  aBDsin  cBDsin ，……………………9’ 2 3 2 6 2 6 即ac2(ac)，……………………10’ 由基本不等式得ac2(ac)4 ac ，故ac16，当且仅当a=c=4时等号成立，…………12’ （等号成立的条件没写，扣1分） 1  1  S  acsin  16sin 4 3，故 ABC面积的最小值为4 3．……………………13’ △ABC 2 3 2 3  第 4 页 共 8 页16．解：（1）方法1：  PA底面ABCD，底面ABCD是正方形， BD  PA，BD  AC， …………………………………………………………1’ 又 PA AC  A   BD 平面PAC …………………………………………………………2’  AF 平面PAC BD  AF ① …………………………………………………………3’ 3 2 3 6 在Rt PAE中，PA3，AE  ，PE  PA2  AE2  ……………………4’  2 2 2 PA 6 PE 则PF  PE  6,故   ，又FPAAPE，所以 PFA∽ PAE ………………5’   3 PF 2 PA 因此，PFAPAE 90,故PE  AF ② ……………………………………………………6’ 又 BD PE  E ③   由①②③可知AF 平面PBD ……………………………………………………7’ (缺条件PA AC  A,BD PE  E，仅扣1分，不重复扣分)   方法2：∵PA⊥底面ABCD，AB、AD ⊂平面ABCD， ∴ 𝑃𝐴⊥ 𝐴𝐵，𝑃𝐴⊥ 𝐴𝐷， 又底面𝐴𝐵𝐶𝐷是正方形， ∴ 𝐴𝐵 ⊥ 𝐴𝐷， ∴ 𝑃𝐴、𝐴𝐵、𝐴𝐷两两垂直， …………………………………………………………1’ 以𝐴为原点，𝐴𝐵所在直线为𝑥轴，𝐴𝐷所在直线为𝑦轴，𝐴𝑃所在直线为𝑧轴，建立空间直角坐标系， 3 3  由PA AB3，得A0,0,0,B3,0,0,C3,3,0,D0,3,0,P0,0,3, E , ,0 …………………2’ 2 2  故  P  E     3 , 3 ,3  ,由PF2FE得  P  F   2 P  E  1,1,2,所以F1,1,1, …………………3’ 2 2  3  B  D  3,3,0,  P  B  3,0,3，  A  F  1,1,1， …………………4’     由于BDAF 3300,PBAF 3030,     因此BD AF,PB AF，进而BD AF,PB AF, …………………6’ 又BDPBB,BD,PB平面PBD,故AF 平面PBD； …………………7’ 第 5 页 共 8 页  （2）AF 1,1,1,AD0,3,0， …………………8’ 设平面AFD的法向量n(x，y，z)， n·  A  F  xyz0 则 n·  A  D  3y0 ，取x1，得n 1,0,1， …………………10’ 平面CFD的法向量m a,b,c，C  F  2,2,1,  D  C  3,0,0 …………………11’ m·C  F  2a2bc0  则 m·  D  C  3a0 ，取b1，得m0,1,2， …………………13’ |m n| 2 10 设平面AFD与平面CFD的夹角，则cos    ．…………………15’ |m|  |n| 2 5 5 17．解：(1)设“甲中靶”为事件𝐴，“乙中靶”为事件𝐵， ………………1’(设事件) “甲、乙两人恰好有一人中靶”为事件𝐷，则 𝐷=𝐴𝐵+𝐴𝐵，其中𝐴𝐵与𝐴𝐵互斥．……………………………………2’（表示所求事件） 3 2 由题意得，𝑃(𝐴)= ，𝑃(𝐵)= ，且事件𝐴、𝐵相互独立，………3’（没写相互独立，扣1分） 5 5 则𝑃 𝐷 =𝑃 𝐴𝐵+𝐴𝐵 =𝑃 𝐴𝐵 +𝑃 𝐴𝐵 =𝑃 𝐴 𝑃 𝐵 +𝑃 𝐴 𝑃 𝐵 ………………5’ =𝑃 𝐴 1−𝑃 𝐵 + 1−𝑃 𝐴 𝑃 𝐵 3 2 3 2 = × 1− + 1− × ………………………………………………………………6’ 5 5 5 5 13 = ……………………………………………………………………………………………7’ 25 13 所以甲、乙两人恰好有一人中靶的概率为 ； ……………………………8’（作答1分） 25 (2)设“丙中靶”为事件𝐶，“甲、乙、丙三个人中至少有一人中靶”为事件𝐸，…………9’ 易知𝐸=𝐴𝐵𝐶，且𝐴、𝐵、𝐶相互独立，……………………………………10’ 则由题意，𝑃 𝐸 =𝑃 𝐴𝐵𝐶 =𝑃 𝐴 𝑃 𝐵 𝑃 𝐶 = 1−𝑃 𝐴 1−𝑃 𝐵 1−𝑃 𝐶 …………………12’ 3 2 𝑛 2 3 𝑛 6 𝑛 22 3 = 1− 1− 1− = × 1− = 1− =1− = ………………………14’ 5 5 20 5 5 20 25 20 25 25 解得𝑛 =10． ………………………15’ 18．解：（1）设Qx,y ，P(x ,y )，由题意得x 22  y2 4， …………………1’ 0 0 0 0 x x2 x 2x 又点B是点P(x ,y )与点Qx,y 的中点，则 0 ，于是 0 …………………3’ 0 0 y  y 0 y y   0 0 代入x 22  y2 4得x2  y2 4，此即点Q的轨迹方程． …………………4’ 0 0 第 6 页 共 8 页（2） QB 2  QC 2 x12  y2 x52 y82 2x2 2y2 12x16y90 ……………6’ 12x16y9843x4y98 …………………7’ 3 1 1 3 1 令z3x4y，则y x z， z可视为直线y x z在y轴上的截距， 4 4 4 4 4 3 1 1 3x4y的最小值就是直线y x z与圆x2  y2 4相切时纵截距 z最小值的4倍 ……8’ 4 4 4 z 直线与圆相切时，圆心到直线3x4yz0的距离等于半径，即d  2，所以z 10. ……9’ min 5 2 2 因此 QB  QC 的最大值为138. …………………10’ （3）存在点M1,0 ，使得M  E  M  F  为定值3. 当直线l的斜率存在时，设其斜率为k，则直线l的方程为 y kx1 ， x2  y2 4 由 ，消去y，得  1k2 x2 2k2xk2 40，显然0，…………………11’  y kx1 2k2 k2 4 设Ex ,y  ，Fx ,y  则x x  ，x x  ，…………………12’ 1 1 2 2 1 2 1k2 1 2 1k2   又ME mx ,y ，MF mx ,y ， 1 1 2 2   则MEMF m2 mx x x x  y y m2 mx x x x k2x 1x 1 1 2 1 2 1 2 1 2 1 2 1 2 k2 4 2k2   1k2 x x   mk2x x   m2 k2   1k2   mk2   m2 k2 1 2 1 2 1k2 1k2  m2 2m2  k2 m2 4  …………………15’ k2 1 要使上式恒为定值，需满足m2 2m2m2 4， 解得m 1，此时M1,0 ，M  E  M  F  为定值3. …………………16’ 当直线l的斜率不存在时，E  1, 3  ，F  1, 3  ，由M1,0 可得M  E  M  F  3. 所以存在点M1,0 ，使得M  E  M  F  为定值3. …………………17’ 第 7 页 共 8 页19．解：(1)由△𝐹 𝑀𝑁的周长为16，及椭圆的定义，可知：4𝑎=16，即𝑎=4，………………1’ 1 c 1 又离心率为e  ，所以c2，……………………………………2’ a 2 𝑏2 =𝑎2−𝑐2 =16−4=12，……………………………………3’ x2 y2 所以椭圆𝐶的方程为：  1．……………………………………4’ 16 12 (2)依题意，直线𝑙与𝑥轴不重合，设𝑙的方程为：𝑥=𝑚𝑦+2．……………………………………5’ x2 y2   1 联立16 12 得： 3𝑚2+4 𝑦2+12𝑚𝑦−36= 0，……………………………………6’  xmy2 因为𝐹 在椭圆内，所以𝛥>0，即 12𝑚 2+4 3𝑚2+4 ×36>0，易知该不等式恒成立， 2 设𝑀 𝑥 ,𝑦 ,𝑁 𝑥 ,𝑦 ，则 1 1 2 2 −12𝑚 −36 𝑦 +𝑦 = ,𝑦 𝑦 = ．……………………………………7’ 1 2 3𝑚2+4 1 2 3𝑚2+4 又𝐴(−4,0)，𝐵(4,0)，则 𝑆 = 1 |𝐴𝐵||𝑦 −𝑦 |= 4|𝑦 −𝑦 |= 4 (𝑦 +𝑦 )2−4𝑦 𝑦 …………………………8’ 𝐴𝑀𝐵𝑁 1 2 1 2 1 2 1 2 2 −12𝑚 2 −36 96 𝑚2+1 96 𝑚2+1 96 =4× −4× = = = ………………10’ 3𝑚2+4 3𝑚2+4 3𝑚2+4 3(𝑚2+1)+1 1 3 𝑚2+1+ 𝑚2+1 96 令𝑡= 𝑚2+1 𝑡≥1 ，易知 在 1,+∞ 上单调递减，故…………………………………………11’ 1 3𝑡+ 𝑡 96 96 𝑆 = ≤ =24 𝐴𝑀𝐵𝑁 1 3+1 3𝑡+ 𝑡 四边形𝐴𝑀𝐵𝑁面积的最大值为24．…………………………………………………………………12’ (3)由题意知 𝑦 1 𝑘 𝑥 +4 𝑦 𝑥 −4 𝑦 𝑚𝑦 −2 𝑚𝑦 𝑦 −2𝑦 1 = 1 = 1 2 = 1 2 = 1 2 1 …………………………14’ (代入消去𝒙，并化简正确) 𝑦 𝑘 2 𝑦 𝑥 +4 𝑦 𝑚𝑦 +6 𝑚𝑦 𝑦 +6𝑦 2 2 1 2 1 1 2 2 𝑥 −4 2 𝑦 +𝑦 −12𝑚 𝑚 注意到 1 2 = = ，即：𝑚𝑦 𝑦 =3 𝑦 +𝑦 ，则 ……………………………………15’ 1 2 1 2 𝑦 𝑦 −36 3 1 2 𝑘 𝑚𝑦 𝑦 −2𝑦 3(𝑦 +𝑦 )−2𝑦 𝑦 +3𝑦 1 1 = 1 2 1 = 1 2 1 = 1 2 = ．……………………………………17’ 𝑘 𝑚𝑦 𝑦 +6𝑦 3(𝑦 +𝑦 )+6𝑦 3𝑦 +9𝑦 3 2 1 2 2 1 2 2 1 2 第 8 页 共 8 页