数学答案_2024-2025高二（7-7月题库）_2024年12月试卷_1219四川省达州市万源中学2024-2025学年高二上学期第二次月考

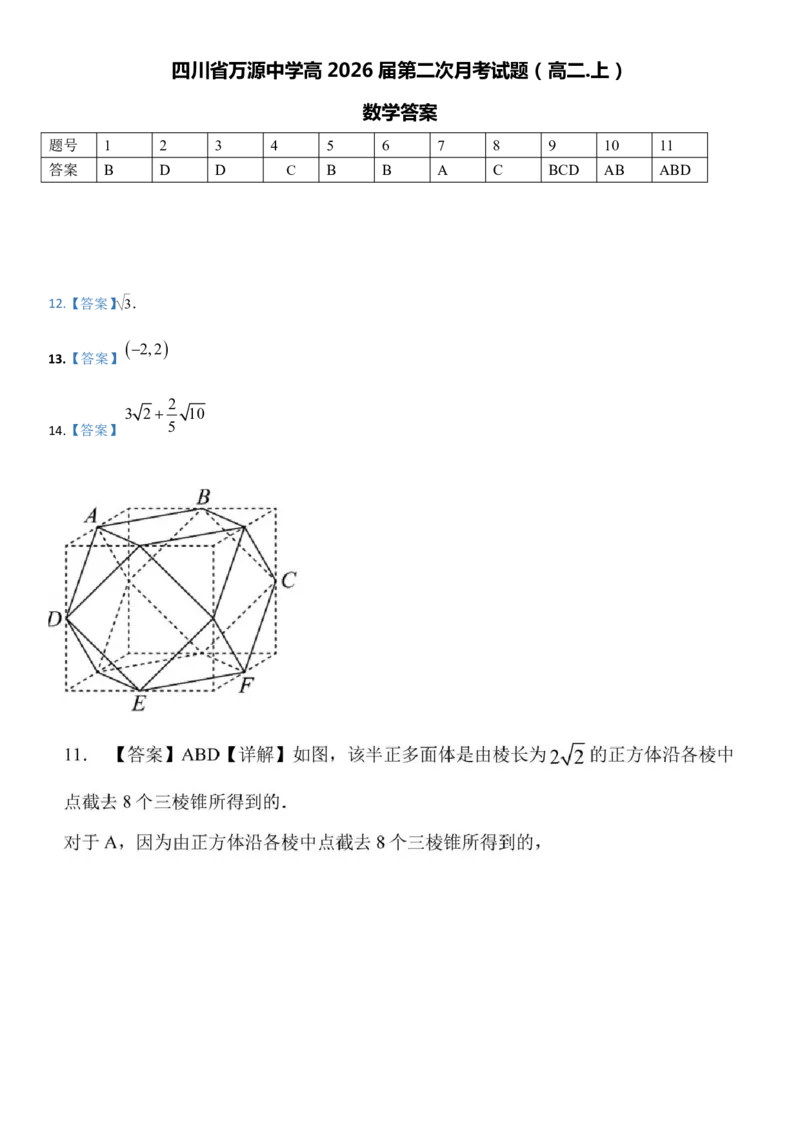
四川省万源中学高 2026 届第二次月考试题（高二.上） 数学答案 题号 1 2 3 4 5 6 7 8 9 10 11 答案 B D D C B B A C BCD AB ABD 12.【答案】3． 2,2  13.【答案】 2 3 2 10 14.【答案】 514. |ab3| |5a3b3| 【详解】由已知得，t 0，整理得  t， a2 b2 a2 b2 看成有且仅有三条直线满足，A(1,1)和B(5,3)到直线l:axby30（不过原点）的距离t相等； 由| AB| (51)2 (31)2 4 2， | AB| （1）当t  2 2，此时，易得符合题意的直线l为线段AB的垂直平分线以及直线AB平行的两条直线. 2 | AB| （2）当t  2 2时，有4条直线l会使得点A(2,1)和B(5,3)到它们的距离相等， 2 注意到l不过原点，所以当其中一条直线过原点时，会作为增根被舍去；设点A到l的距离为d， ①作为增根被舍去的直线l，过原点和A，B的中点M(3,1)，其方程为x3y0， 2 此时，t d  10 2 2，符合； 5  ②作为增根被舍去的直线l，过原点且以 AB 为方向向量，其方程为x y0， 此时，t d  2 2 2，符合； 2 2 2 综上，满足题意的实数t为2 2， 10， 2，它们的和为2 2 10 2 3 2 10. 5 5 5 2 故答案为：3 2 10 5 【点睛】关键点点睛：本题考查了点到直线距离公式的应用以及方程组解的个数问题解法，解题的关键是把问题转 化为有且仅有三条直线满足A(1,1)和B(5,3)到直线l:axby30（不过原点）的距离t相等，属于难题.15.①解法一：∵椭圆的焦点在y轴上， y2 x2 ∴设所求椭圆的标准方程为 ＋ ＝1(a＞b＞0)． a2 b2 由题意知c＝2， 2a＝ （4－0）2＋（3 2＋2）2＋ （4－0）2＋（3 2－2）2＝12， 解得a＝6． ∴b2＝a2－c2＝32． y2 x2 ∴所求椭圆的标准方程为 ＋ ＝1． 36 32 解法二：∵椭圆的焦点在y轴上， y2 x2 ∴设所求椭圆的标准方程为 ＋ ＝1(a>b>0)． a2 b2 18 16 ＋ ＝1， a2＝36， 由题意得 a2 b2 解得 a2－b2＝4， b2＝32. y2 x2 ∴所求椭圆的标准方程为 ＋ ＝1． 36 32 x2 y2 ②解法一：(ⅰ)当椭圆的焦点在x轴上时，设椭圆的标准方程为 ＋ ＝1(a>b>0)， a2 b2 1 1 2 2 3 3 ＋ ＝1， 1 a2 b2 a2＝ ， 5 依题意知 1 解得 － 2 1 2 b2＝ . ＝1， 4 b2 1 1 ∵a2＝ < ＝b2， 5 4 ∴焦点在x轴上的椭圆不存在． (ⅱ)当椭圆的焦点在y轴上时， y2 x2 设椭圆的标准方程为 ＋ ＝1(a>b>0)． a2 b2 1 1 2 2 3 3 ＋ ＝1， 1 a2 b2 a2＝ ， 4 由题意得 1 解得 － 2 1 2 b2＝ . ＝1， 5 a2 y2 x2 故所求椭圆的标准方程为 ＋ ＝1． 1 1 4 5 解法二：设所求椭圆的方程为Ax2＋By2＝1(A>0，B>0，A≠B)．1 1 2 2 A× 3 ＋B× 3 ＝1， 由题意得 1 － 2 B× 2 ＝1， A＝5， 解得 B＝4， 故所求椭圆的方程为5x2＋4y2＝1， y2 x2 即椭圆的标准方程为 ＋ ＝1． 1 1 4 5 15（1）设点M(x，y)，点P(x ，y )， 0 0 x x＝ 0， 2 x ＝2x， 0 则 ∴ y y＝ 0， y ＝2y. 0 2 ∵点P(x ，y )在圆C：x2＋y2－8x－6y＋21＝0上， 0 0 ∴x2＋y2－8x －6y ＋21＝0． 0 0 0 0 ∴(2x)2＋(2y)2－8·(2x)－6·(2y)＋21＝0． 3 21 y－ 2 即线段OP的中点M的轨迹方程为x2＋y2－4x－3y＋ ＝0．或者(x－2)2＋ 2 ＝1． 4 （2）设圆P的半径为r．∵圆P过点B，∴|PB|＝r．又圆P与圆A内切，圆A的半径为10．∴两圆的圆心距|PA| ＝10－r，即|PA|＋|PB|＝10(大于|AB|)．∴点P的轨迹是以A，B为焦点的椭圆．∴2a＝10，2c＝|AB|＝6，∴a＝5，c x2 y2 ＝3．∴b2＝a2－c2＝25－9＝16．即圆心P的轨迹方程为 ＋ ＝1． 25 16 16.BC边上的中线所在直线的方程为y＝3， y＝3， x＝－1， 由 解得 y＝3x＋6， y＝3， 所以点A的坐标为(－1，3)． 设点C(x ，y )，则BC的中点在直线y＝3上， 1 1 y ＋0 所以 1 ＝3， 2 即y ＝6， 1 又点C(x ，6)在直线x＋3y－26＝0上，所以C(8，6)， 1 6－3 1 所以AC的斜率k ＝ ＝ ， AC 8＋1 3 1 所以直线AC的方程为y－6＝ (x－8)， 3 即x－3y＋10＝0．(1)因为AB边上的高所在直线的方程为x＋3y－26＝0， 所以直线AB的斜率k＝3，又因为△ABC的顶点B(－2，0)， 所以直线AB的方程为y＝3(x＋2)，即3x－y＋6＝0．1 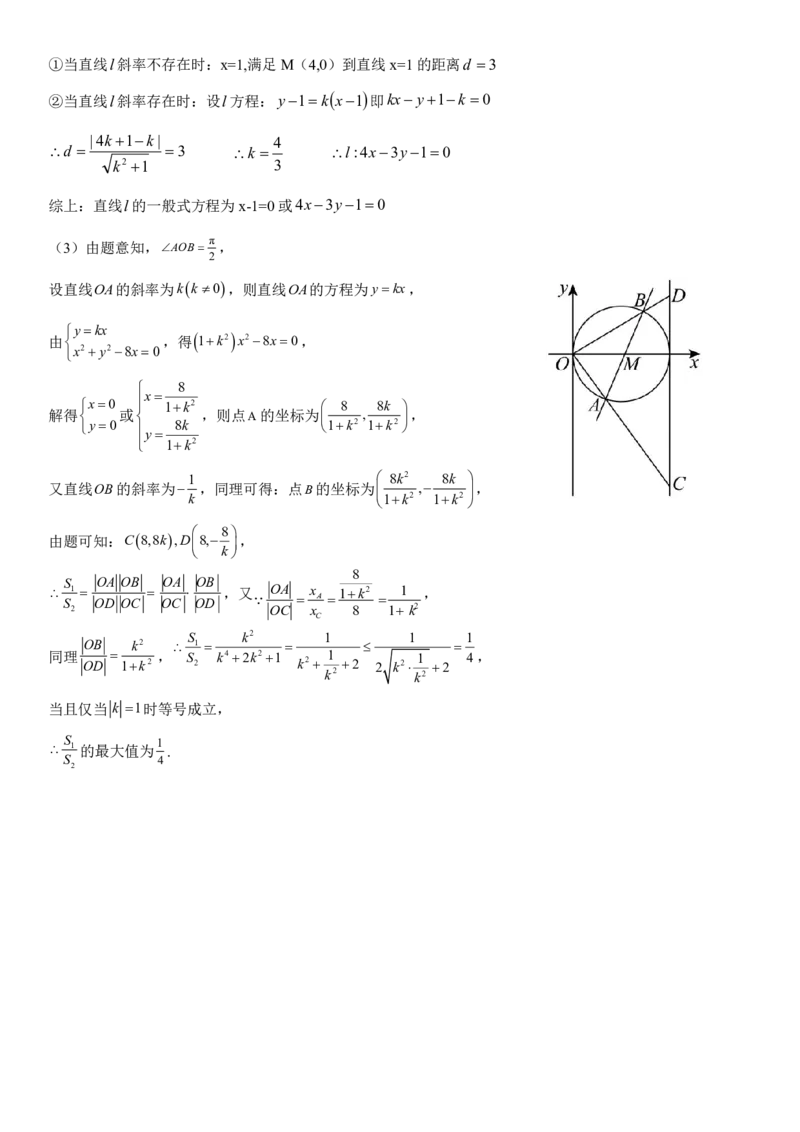19．【答案】(1)(x4)2y2 16 ； (2)x10或4x3y10；(3) . 4 【解】（1）由题可知，设圆的方程为(xa)2 y2 r2，   由直线3x 7y40与圆相切于点 1, 7 ， (1a)27r2  得 7 3 ，解得a4,r4，所以圆的方程为(x4)2y2 16；   1 1a 7 （2）设圆心M（4,0）到直线l的距离为d ∵|PQ|=2 r2 d2 ∴ 2 7  16d2 d 3①当直线l斜率不存在时：x=1,满足M（4,0）到直线x=1的距离d 3 ②当直线l斜率存在时：设l方程：y1k  x1  即kx y1k 0 |4k1k| 4 d  3 k  l:4x3y10 k2 1 3 综上：直线l的一般式方程为x-1=0或4x3y10 π （3）由题意知，AOB ， 2 设直线OA的斜率为kk 0，则直线OA的方程为ykx， ykx 由 ，得  1k2 x28x0， x2y28x0  8 x x0   1k2  8 8k  解得 或 ，则点A的坐标为 , ， y0  y 8k 1k2 1k2   1k2 1  8k2 8k  又直线OB的斜率为 ，同理可得：点B的坐标为 , ， k 1k2 1k2   8 由题可知：C8,8k,D8, ，  k  8 S OA OB OA OB  1    ，又 OA x 1k2 1 ， S OD OC OC OD   A   2 OC x 8 1 k2 C S k2 1 1 1 OB k2  1     同理 OD  1k2 ， S 2 k42k21 k2 1 2 2 k2 1 2 4， k2 k2 当且仅当 k 1时等号成立， S 1  1 的最大值为 . S 4 2