数学答案_2024-2025高二（7-7月题库）_2025年05月试卷_0511四川省南充市嘉陵一中2024-2025学年高二下学期4月期中考试

数学答案
一、单项选择题：1-4CBAA 5-8CCAA
二、多项选择题：
9. ACD 10.BD 11.ACD
12. 720 13. (0,3) 14. a n2，nN
n
8,【详解】令m1，得到a a a 3a ，故数列是等比数列， a 33n1 3n， a 32n1
1 n 1n n n 2n1
log a log a log a 12...  2n1 n  2n1 
3 1 3 2 3 2n1
11【详解】对于选项A，因为 f  x ax33x2 1，则 f x 3ax2 6x3x  ax2  ，
2 2 2
当a0时，令 f x 0，得到x0或x ，当x0或x 时，f x 0，当0 x 时，f x 0，
a a a
2 2 4
所以x0是 f  x  的极大值点，极大值为 f  0 1，x 是 f  x  极小值点，极小值为 f( ) 1，
a a a2
当a 0时， f(x)3x21，由极值的定义知， f (x)的极大值为1，无极小值，
2 2 2
当a 0时，令 f x 0，得到x0或x ，当x 或x 0时，f x 0，当  x0时，f x 0，
a a a
2 2 4
所以x0是 f  x  的极大值点，极大值为 f  0 1，x 是 f  x  极小值点，极小值为 f( ) 1，
a a a2
综上，1是 f (x)的极大值，所以选项A正确，
2 
 
对于选项B，因为1 a 0，由选项A知， f x 在区间 ,0上单调递增，
a 
2
又1 a 0，则 ,2 ，2a11，所以 f(a1) f(a)，故选项B错误，
a
2 2   2
对于选项C，当a2时， 1，由选项A知， f  x  的增区间为 ,0  ， , ，减区间为0, ，
a a   a
当x时， f  x ， f (0) 10， f  2 8a1218a130，
由零点存在性原理知，当a2时， f (x)有且仅有一个零点x ，且x 2，所以选项C正确，
0 0
2 2
对于选项D，因为 f  x  存在极小值点x，由选项A知，x  ，得到a ，
1 1 a x
1
2 2
因为 f(x ) f(x )，则 x33x2 1 x33x2 1，整理得到2x3 3x x2 x3 0，
1 2 x 1 1 x 2 2 2 1 2 1
1 1
第1页/共4页
学科网（北京）股份有限公司即 x x 2 x 2x 0，又x  x ，所以x 2x 0，故选项D正确，
1 2 1 2 1 2 1 2
 
14.记由n2个数构成递增的等比数列为 b ，
n
则b=1，b =100，则qn1=100，即n1lgq=lg1002
1 n2
所以T =b b b b ，
n 1 2 3 n2
即a lg  b b b b  =lgb lg  bq lg  bq2  lg  bqn1 
n 1 2 3 n2 1 1 1 1
=  n2  lgb 

123+  n1 

lgq
1
 n1  n2 
= lgq n2
2
15. 解：（1）由题知，该五位数个位数为奇数，然后余下的四个数全排列即可.
C1A4 72个.
3 4
（2）先对1,3,5三个数全排列，然后利用插空法排列2和4,即A3A2 72个
3 4
（3）从5个数中挑选出重复的数字，从剩下的4个数中挑选3个数字，先对重复数字排列，然后余下的三
个数全排列即C1C3C2A3 1200个
5 4 5 3
16.(1)在 12x 2 12x 3 12x n9a xa x2a x n中，
1 2 n
令x0，得n19，所以n10.
在 12x 2 12x 3 12x 10 9a xa x2a x10中，
1 2 10
令x1，得9a a a a a 11111111，
1 2 3 9 10
所以  a a a   a a a  8.
1 3 5 2 4 6
(2)∵ 12x n的展开式的通项公式为T Cr  2x r 2rCrxr，
r1 n n
   
∴a 22 C2 C2 C2 C2 4 C3 C2 C2 C2 4C3 660
2 2 3 4 10 3 3 4 10 11
17.（1）证明：因为数列  a  满足a 2a 1  nN*  ，
n n1 n
a 1
可得a 12(a 1)，即 n1 2，
n1 n a 1
n
又因为a 3，可得a 12，所以数列 a 1 是首项为2，公比为2的等比数列.
1 1 n
第2页/共4页
学科网（北京）股份有限公司（2）解：由（1）知，数列 a 1 是首项为2，公比为2的等比数列，
n
可得a 122n1 2n，所以a 2n 1，
n n
则数列  a  的前n项和为T 
2(12n)
n 2n1n2.
n n 12
（3）解：由（2）知：a 1 2n，可得b log  a 1 log 2n n，
n n 2 n 2
1 1 1 1
所以    ，
b b n(n1) n n1
n n1
1 1 1 1 1 1 1 1
所以S b b b (1 )(  )(  )(  )1 ，
n 1 2 n 2 2 3 3 4 n n1 n1
1
当nN时，S 1 为单调递增数列，
n n1
1
当n1时，S 取得最小值，最小知为S  ，
n 1 2
1 1
又因为 0，可得S 1，所以  S 1.
n1 n 2 n
1
18.（1）因为 f  x lnx 1a  x1，所以 f x   1a  .
x
因为 x 0，若1a0，即a1时， f

x

在
 0,
上单调递增，
1 1
若1a0，即a1时，令 f x   1a 0，得0 x ；
x a1
1 1  1   1 
令 f x   1a 0，得x  ，所以 f  x  在0, 上单调递增，在 , 上单调递减.
x a1  a1 a1 
 1   1 
综上，当a1时，f  x  在  0, 上单调递增；当a1时，f  x  在0, 上单调递增，在 , 
 a1 a1 
上单调递减.
（2）因为 f  x lnx 1a  x1， f  x1 ex  a1  x2(a1)恒成立，
所以ln(x1) 1a  (x1)1ex  a1  x2(a1)，则aex ln(x1)，
1
令g  x ex ln(x1)且x1，则g x ex  ，
x1
1
令h  x  g(x)，则h x ex  0，故h  x  g(x)在 1, 上单调递增，
(x1)2
又g
0
0，所以x1,0  时，g
x
0；x 0, 时，g
x
0，
第3页/共4页
学科网（北京）股份有限公司所以g

x

在
1,0 
上单调递减，在
 0,
上单调递增，g

x

g

0
1，
所以a1，实数a的取值范围为 ,1  .
19.（1）因为 f  x ex ax，所以 f x ex a，
当a0时， f x ex a0，则 f  x ex ax在R上单调递增，
当a0时，令 f x ex a0得xlna，令 f x ex a0得xlna，
所以函数 f  x  的增区间为(lna,)，减区间为(,lna)，
令F  x ex 2x，则Fxex 2，令F x ex 20得xln2，
令F x ex 20得xln2，所以函数F  x  的增区间为(ln2,)，减区间为(,ln2)，
所以当xln2时，F  x  取得最小值为F  ln2 eln2 2ln222ln20，
所以ex 2x，得证；
（2）由（1）知，g  x ex axcosx ，
因为函数g

x

在区间
 0,
内有唯一的零点，所以方程aex xcosx在区间
 0,
内有唯一解，
令h(x)ex xcosx,x0，则函数h(x)ex xcosx与 y a在  0, 上只有一个交点，
记m  x ex x1,(x0) ，则m x ex 10，所以m  x  在  0, 上单调递增，
所以m  x ex x1e010，即ex  x1，
故h(x)ex cosxxsinx1cosxx(1sinx)0 ，
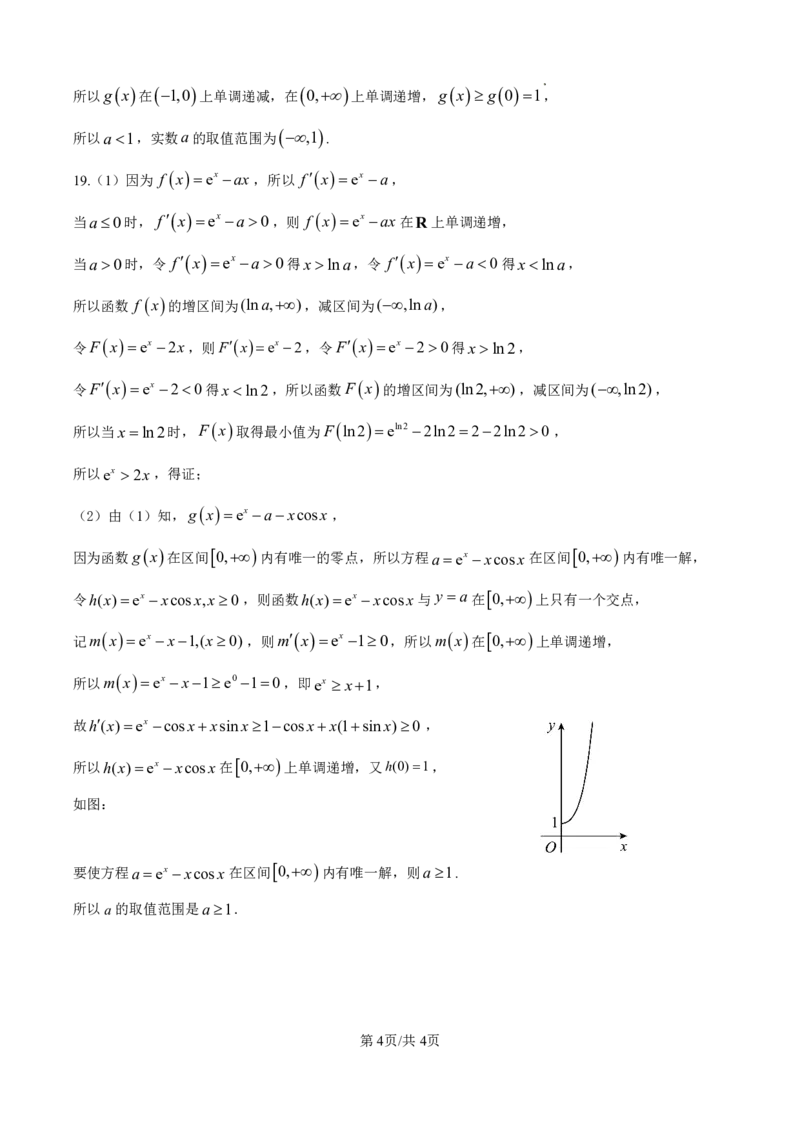
所以h(x)ex xcosx在  0, 上单调递增，又h(0)1，
如图：
要使方程aex xcosx 在区间
 0,
内有唯一解，则a1.
所以a的取值范围是a1.
第4页/共4页
学科网（北京）股份有限公司