文档内容
200 2 年河南高考数学真题及答案
一、选择题(共12小题,每小题5分,满分60分)
1.(5分)函数 的最小正周期是
A. B. C. D.
2.(5分)圆 的圆心到直线 的距离是
A. B. C.1 D.
3.(5分)不等式 的解集是
A. B. 且 C. D. 且
4.(5分)在 内,使 成立的 的取值范围是
A. , , B. ,
C. , D. , ,
5.(5分)已知集合 , , , ,则
A. B. C. D.
6.(5分)一个圆锥和一个半球有公共底面,如果圆锥的体积与半球的体积恰好相等,则
圆锥轴截面顶角的余弦值是
A. B. C. D.
7.(5分)函数 是奇函数的充要条件是
A. B. C. D.
8.(5分)已知 ,则有
A. B. C. D.
9.(5分)函数
第1页 | 共15页A.在 内单调递增 B.在 内单调递减
C.在 内单调递增 D.在 内单调递减
10.(5分)极坐标方程 与 的图形是
A. B.
C. D.
11.(5分)从正方体的6个面中选取3个面,其中有2个面不相邻的选法共有
A.8种 B.12种 C.16种 D.20种
12.(5分)据2002年3月5日九届人大五次会议《政府工作报告》:“2001年国内生产
总值达到95933亿元,比上年增长 ”,如果“十 五”期间 年 年)每
年的国内生产总值都按此年增长率增长,那么到“十 五”末我国国内年生产总值约为
A.115000亿元 B.120000亿元 C.127000亿元 D.135000亿元
二、填空题(共4小题,每小题4分,满分16分)
13.(4分)椭圆 的一个焦点是 ,那么 .
14.(4分)在 的展开式中 的系数是 .
15.(4分)已知 , ,则 .
16.(4分)已知函数 ,那么
.
三、解答题(共6小题,满分74分)
17.(12分)已知复数 ,求实数 , 使 .
18.(12分)设 为等差数列, 为等比数列, , , ,
第2页 | 共15页分别求出 及 的前10项的和 及 .
19.(12分)四棱锥 的底面是边长为 的正方形, 平面 .
(1)若面 与面 所成的二面角为 ,求这个四棱锥的体积;
(2)证明无论四棱锥的高怎样变化.面与面所成的二面角恒大于 .
20.(12分)设 、 是双曲线 上的两点,点 是线段 的中点.
求直线 的方程
如果线段 的垂直平分线与双曲线相交于 、 两点,那么 、 、 、 四点是
否共圆?为什么?
21.(12分)(1)给出两块相同的正三角形纸片(如图1,图 ,要求用其中一块剪拼
成一个三棱锥模型,另一块剪拼成一个正三棱柱模型,使它们的全面积都与原三角形的
面积相等,请设计一种剪拼方法,分别用虚线标示在图1、图2中,并作简要说明;
(2)试比较你剪拼的正三棱锥与正三棱柱的体积的大小;
(3)如果给出的是一块任意三角形的纸片(如图 ,要求剪拼成一个直三棱柱,使它的
全面积与给出的三角形的面积相等.请设计一种剪拼方法,用虚线标示在图3中,并作
简要说明.
22.(14分)已知 ,函数 .
(1)当 时,若对任意 都有 ,证明 ;
(2)当 时,证明:对任意 , , 的充要条件是 ;
(3)当 时,讨论:对任意 , , 的充要条件.
第3页 | 共15页参考答案
一、选择题(共12小题,每小题5分,满分60分)
1.(5分)函数 的最小正周期是
A. B. C. D.
【解答】解:函数 ,所以函数的最小正周期为:
故选: .
2.(5分)圆 的圆心到直线 的距离是
A. B. C.1 D.
【解答】解:由 得:圆心 ,
所以根据点到直线的距离公式得:
.
故选: .
3.(5分)不等式 的解集是
A. B. 且 C. D. 且
【解答】解:求不等式 的解集
则分两种情况讨论:
情况 即:
则: .
情况 即:
则:
两种情况取并集得 且 .
第4页 | 共15页故选: .
4.(5分)在 内,使 成立的 的取值范围是
A. , , B. ,
C. , D. , ,
【解答】解: ,
,
,
在 内,
,
故选: .
5.(5分)已知集合 , , , ,则
A. B. C. D.
【解答】解:对于 的元素,有 ,其分子为 的奇数倍;
对于 的元素,有 ,其分子为 的整数倍;
分析易得, ;
故选: .
6.(5分)一个圆锥和一个半球有公共底面,如果圆锥的体积与半球的体积恰好相等,则
圆锥轴截面顶角的余弦值是
A. B. C. D.
【解答】解:设圆锥的半径为 ,高为 ,母线与轴所成角为 ,则圆锥的高
圆锥的体积
半球的体积
第5页 | 共15页即:
故选: .
7.(5分)函数 是奇函数的充要条件是
A. B. C. D.
【解答】解:根据奇函数的定义可知
对任意 恒成立
, ,故选
8.(5分)已知 ,则有
A. B. C. D.
【解答】解: ,
故选: .
9.(5分)函数
A.在 内单调递增 B.在 内单调递减
C.在 内单调递增 D.在 内单调递减
【解答】解: 是 向右平移1个单位而得到,
故 在 上为增函数,
在 上为增函数.
故选: .
10.(5分)极坐标方程 与 的图形是
A. B.
第6页 | 共15页C. D.
【解答】解: 两边同乘以 得
利用 , , ,进行化简得
与
表示 , 为圆心, 为半径的圆,
表示直线
故选: .
11.(5分)从正方体的6个面中选取3个面,其中有2个面不相邻的选法共有
A.8种 B.12种 C.16种 D.20种
【解答】解:使用间接法,首先分析从6个面中选取3个面,共 种不同的取法,
而其中有2个面相邻,即8个角上3个相邻平面,选法有8种,
则选法共有 种;
故选: .
12.(5分)据2002年3月5日九届人大五次会议《政府工作报告》:“2001年国内生产
总值达到95933亿元,比上年增长 ”,如果“十 五”期间 年 年)每
年的国内生产总值都按此年增长率增长,那么到“十 五”末我国国内年生产总值约为
A.115000亿元 B.120000亿元 C.127000亿元 D.135000亿元
【解答】解:根据题意,有 ,
故选: .
二、填空题(共4小题,每小题4分,满分16分)
13.(4分)椭圆 的一个焦点是 ,那么 1 .
第7页 | 共15页【解答】解:把椭圆方程化为标准方程得: ,
因为焦点坐标为 ,所以长半轴在 轴上,
则 ,解得 .
故答案为:1.
14.(4分)在 的展开式中 的系数是 100 8 .
【解答】解: 的展开式中 的系数等于 展开式的 的系数加上
展开式的 的系数
展开式的通项为
令 ,得 故 展开式的 的系数为
令 得 故 展开式的 的系数为
故展开式中 的系数是
故答案为:1008.
15.(4分)已知 , ,则 .
【解答】解: , ,
, ,或 (舍去),
, ,
故答案为: .
16.(4分)已知函数 ,那么
.
第8页 | 共15页【解答】解: ,
(2) , (3) , (4) , (1)
故答案为:
三、解答题(共6小题,满分74分)
17.(12分)已知复数 ,求实数 , 使 .
【解答】解: ,
因为 , 都是实数,
所以由
得
两式相加,整理得
解得 ,
对应得 ,
所求实数为 , 或 ,
18.(12分)设 为等差数列, 为等比数列, , , ,
第9页 | 共15页分别求出 及 的前10项的和 及 .
【解答】解: 为等差数列, 为等比数列,
,
已知 , ,
,
得
由 , 知 的公差为 ,
,
由 , 知 的公比为 或 .
当 时, ,
当 时, .
19.(12分)四棱锥 的底面是边长为 的正方形, 平面 .
(1)若面 与面 所成的二面角为 ,求这个四棱锥的体积;
(2)证明无论四棱锥的高怎样变化.面与面所成的二面角恒大于 .
【解答】解(1) 平面 , 是 在面 上的射影,
是面 与面 所成二面角的平面角,
第10页 | 共15页而 是四棱锥 的高,
证明:(2)不论棱锥的高怎样变化,棱锥侧面 与 恒为全等三角形.
作 ,垂足为 ,连接 ,则 .
, ,故 是面 与面 所成的二面角的平面角.
设 与 相交于点 ,连接 ,则 .
在 中,
所以,面 与面 所成的二面角恒大于
20.(12分)设 、 是双曲线 上的两点,点 是线段 的中点.
求直线 的方程
如果线段 的垂直平分线与双曲线相交于 、 两点,那么 、 、 、 四点是
否共圆?为什么?
【解答】解: 依题意,记 , , , ,
可设直线 的方程为 ,
代入 ,整理得 ①
, 则是方程①的两个不同的根,
所以 ,且 ,
由 是 的中点得 ,
,
第11页 | 共15页解得 ,
所以直线 的方程为
将 代入方程①得
解出 ,
由 得 , .
即 、 的坐标分别为 和 .
由 垂直平分 ,
得直线 的方程为 ,
即 .
代入双曲线方程,整理得 .②
记 , , , ,以及 的中点为 , ,
则 , 是方程②的两个根.所以 , .
从而 , ;
又
即 、 、 、 四点到点 的距离相等,所以 、 、 、 四点共圆.
21.(12分)(1)给出两块相同的正三角形纸片(如图1,图 ,要求用其中一块剪拼
成一个三棱锥模型,另一块剪拼成一个正三棱柱模型,使它们的全面积都与原三角形的
面积相等,请设计一种剪拼方法,分别用虚线标示在图1、图2中,并作简要说明;
(2)试比较你剪拼的正三棱锥与正三棱柱的体积的大小;
(3)如果给出的是一块任意三角形的纸片(如图 ,要求剪拼成一个直三棱柱,使它的
全面积与给出的三角形的面积相等.请设计一种剪拼方法,用虚线标示在图3中,并作
第12页 | 共15页简要说明.
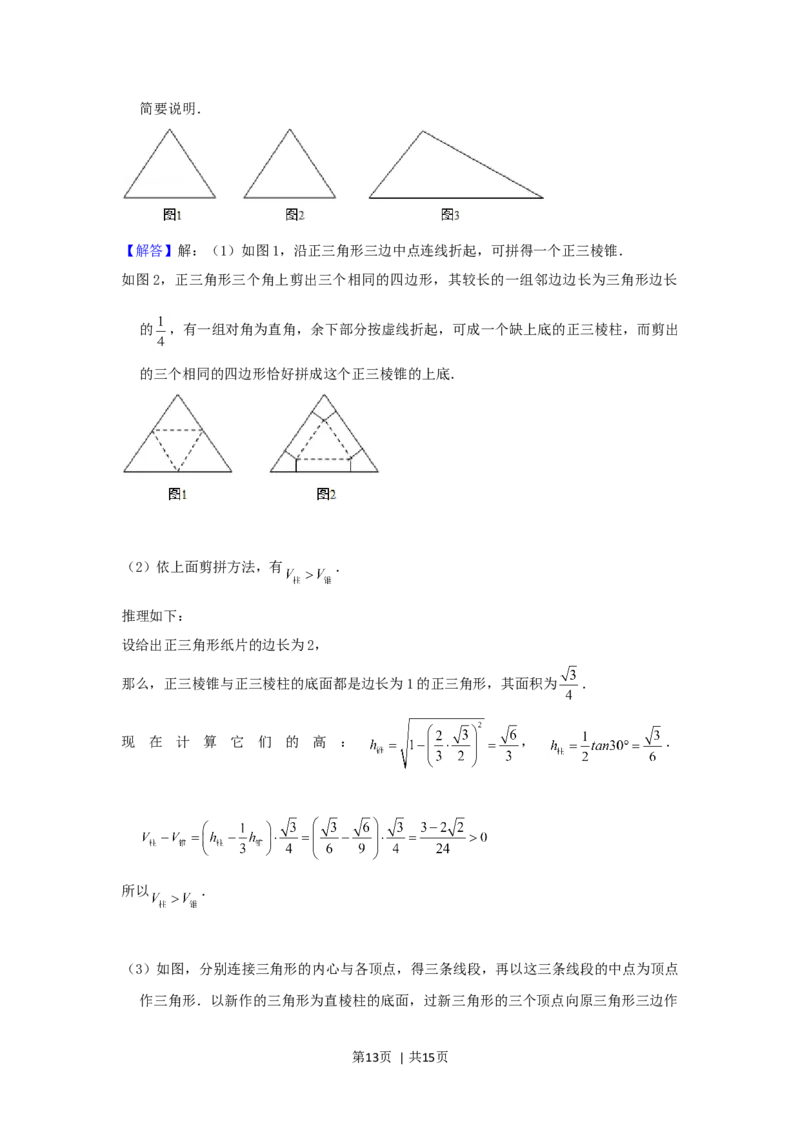
【解答】解:(1)如图1,沿正三角形三边中点连线折起,可拼得一个正三棱锥.
如图2,正三角形三个角上剪出三个相同的四边形,其较长的一组邻边边长为三角形边长
的 ,有一组对角为直角,余下部分按虚线折起,可成一个缺上底的正三棱柱,而剪出
的三个相同的四边形恰好拼成这个正三棱锥的上底.
(2)依上面剪拼方法,有 .
推理如下:
设给出正三角形纸片的边长为2,
那么,正三棱锥与正三棱柱的底面都是边长为1的正三角形,其面积为 .
现 在 计 算 它 们 的 高 : , .
所以 .
(3)如图,分别连接三角形的内心与各顶点,得三条线段,再以这三条线段的中点为顶点
作三角形.以新作的三角形为直棱柱的底面,过新三角形的三个顶点向原三角形三边作
第13页 | 共15页垂线,沿六条垂线剪下三个四边形,可心拼成直三棱柱的上底,余下部分按虚线折起,
成为一个缺上底的直三棱柱,即可得到直三棱柱.
22.(14分)已知 ,函数 .
(1)当 时,若对任意 都有 ,证明 ;
(2)当 时,证明:对任意 , , 的充要条件是 ;
(3)当 时,讨论:对任意 , , 的充要条件.
【解答】(1)证明:根据题设,对任意 ,都有 .
又 . ,
, ,
.
(2)证明:必要性:对任意 , , .
据此可推出 (1) ,即 ,
.
对任意 , , ,
因为 ,可得 ,可推出 ,即 ,
,
.
充分性:因为 , ,对任意 , ,
可以推出 ,即 ,
因为 , 对任意 , ,
可以推出: ,即 ,
第14页 | 共15页.
综上,当 时,对任意 , , 的充要条件是 .
(3)解:因为 , 时,对任意 , 有 ,即
;
(1) ,即 ,
又 ,即 .
所以,当 , 时,对任意 , , 的充要条件是 .
声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布
日期:2019/5/27 22:57:29;用户:15217760367;邮箱:15217760367;学号:10888156
第15页 | 共15页