文档内容
题号 1 2 3 4 5 6 7 8 9 10
答案 A C D A D B C AB BD ACD
1.A
【详解】A.路灯中一个烧坏后,不影响其他路灯正常工作,因此路灯是并联连接的,若
串联,路灯中一个烧坏后,会影响其他路灯正常工作,故A正确;
B.1号干电池的电动势等于5号干电池的电动势,但1号干电池的内阻小于5号干电池的
内阻,故B错误;
C.金属导体通电时建立电场的速率等于光速,自由电子定向移动的速率远小于光速,故C
错误;
D.教室里的八个电灯的电流相等,若八个电灯的电阻相等,当并联时,电压相等,则通
过的电流相等,可知,这八个电灯可能是并联,也可能是串联,故D错误。
故选A。
2.C
【详解】A.摩擦起电的实质是电子从一个物体转移到另一个物体,并没有创造电荷.故
A项错误.
B.感应起电的实质是电荷从物体的一部分转移到另一部分,转移过程中电荷量守恒.故B
项错误.
C.接触起电的实质是电子从一个物体转移到另一个物体,电荷总量保持不变.故C项正
确.
D.等量的正、负电荷可以中和,是电荷的转移,电荷没有被消灭,只是整体不显示电性
而已.故D项错误.
3.D
【详解】AB.仅给出了带电粒子在A、B两点的电势能,无法判断电场是否为匀强电场,
无法计算电场强度且无法计算AB中点的电势及电势能,选项A、B错误;
C.沿电场线方向电势降低,UA 一定为负值,选项C错误;
B
D.把该点电荷从B点由静止释放到经过A点的过程中,电场力做正功,由功能关系可知
E =E -E =4×10-8J
k pB pA
选项D正确。
故选D。
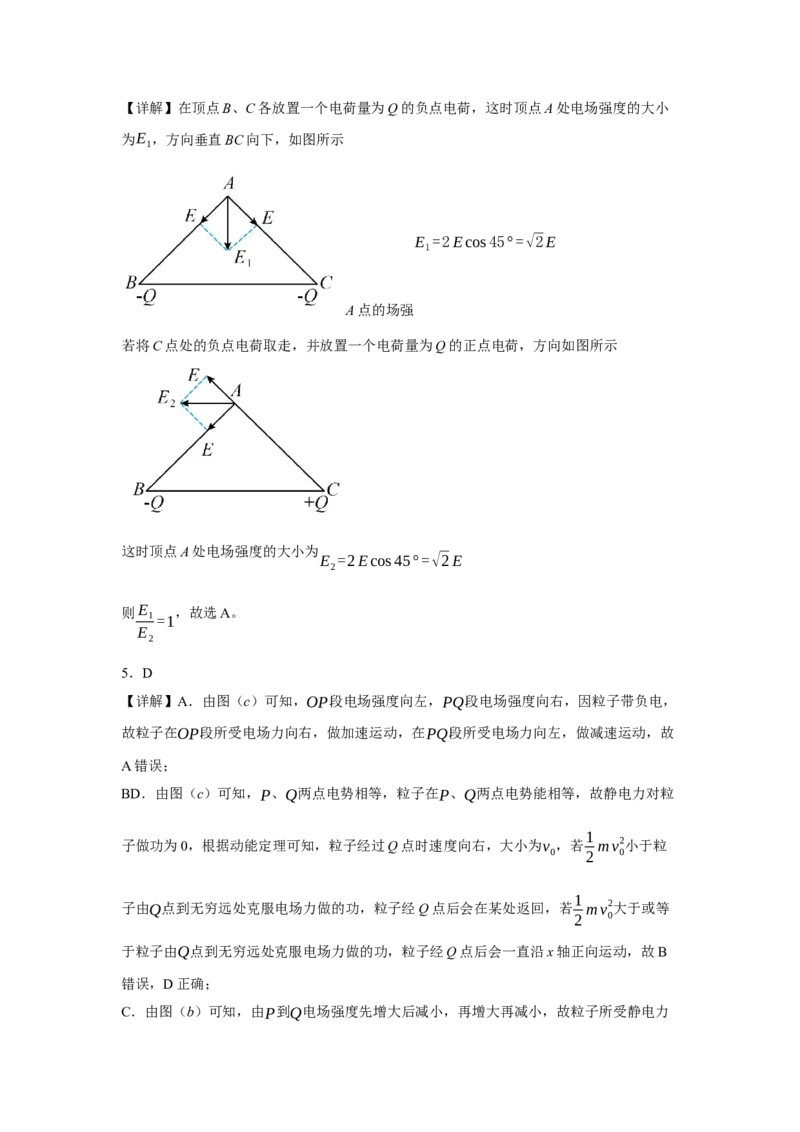
4.A【详解】在顶点B、C各放置一个电荷量为Q的负点电荷,这时顶点A处电场强度的大小
为E ,方向垂直BC向下,如图所示
1
E =2Ecos45°=√2E
1
A点的场强
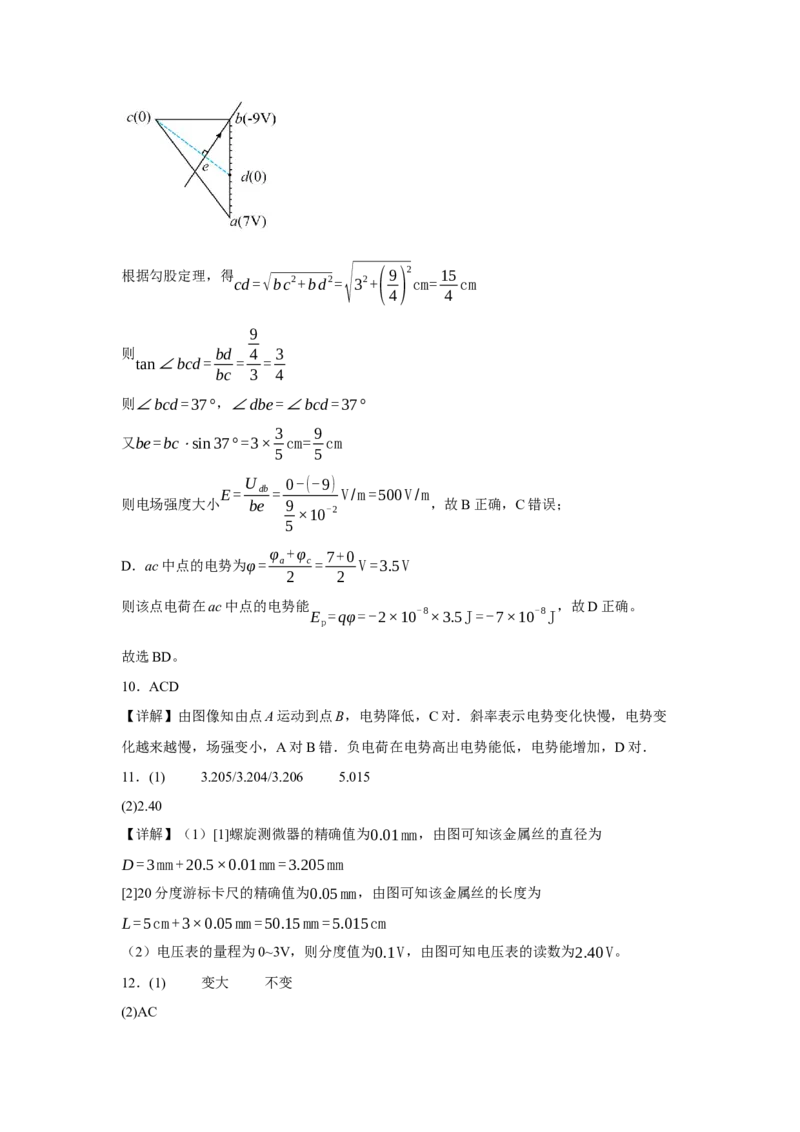
若将C点处的负点电荷取走,并放置一个电荷量为Q的正点电荷,方向如图所示
这时顶点A处电场强度的大小为
E =2Ecos45°=√2E
2
则E ,故选A。
1=1
E
2
5.D
【详解】A.由图(c)可知,OP段电场强度向左,PQ段电场强度向右,因粒子带负电,
故粒子在OP段所受电场力向右,做加速运动,在PQ段所受电场力向左,做减速运动,故
A错误;
BD.由图(c)可知,P、Q两点电势相等,粒子在P、Q两点电势能相等,故静电力对粒
1
子做功为0,根据动能定理可知,粒子经过Q点时速度向右,大小为v ,若 mv2小于粒
0 2 0
1
子由Q点到无穷远处克服电场力做的功,粒子经Q点后会在某处返回,若 mv2大于或等
2 0
于粒子由Q点到无穷远处克服电场力做的功,粒子经Q点后会一直沿x轴正向运动,故B
错误,D正确;
C.由图(b)可知,由P到Q电场强度先增大后减小,再增大再减小,故粒子所受静电力先增大后减小,再增大再减小,故C错误。
故选D。
6.B
【详解】A.电场线由正电荷出发终止于负电荷,则甲带正电、乙带负电,A错误;
B.A、B两点的电势相等,电场强度也可能等大同向,B正确;
C.甲附近的电场线比乙附近的电场线密集,则甲的电荷量大于乙的电荷量,C错误;
D.甲、乙的连线上,有些点附近电场线的疏密程度相同,则存在电场强度相等的两个点,
D项错误。
故选B。
7.C
【详解】B.由题图知,定值电阻与气敏元件串联,电压表测量定值电阻R两端的电压,
当人呼出的酒精气体浓度越大,测试仪中电压表的示数越大,由欧姆定律知,电路的电流
变大,根据P=UI,电路消耗的总功率越大,故B错误;
A.根据串联电路电压的规律,气敏元件电压越小,由分压原理,气敏电阻R 越小,故A
Q
错误;
C.根据P=UI,因定值电阻的电压变大,电路的电流变大,故电压表与电流表的示数乘积
变大,故C正确;
D.由欧姆定律,电压表与电流表的示数之比即定值电阻大小,比值不变,故D错误。
故选C。
8.AB
【详解】AB.若α=37∘, A点速度取得最大值时
v2
√4
mgcosα=m A ,v = gR
R A 5
从A点运动到B点,由动能定理,有
1 1 1
mv2 = mv2+mg⋅ R
2 A 2 B 5
得到
√2
v = gR<√gR
B 5
满足题意,AB正确;
C.若α=53∘,A点速度取得最大值时v2
√3
mgcosα=m A ,v = gR
R A 5
从A点运动到B点,由动能定理,有
1 1 2
mv2 = mv2+mg⋅ R
2 A 2 B 5
得到
1
mv2<0
2 B
不符合题意,C错误;
√4
D.若物块在A点的初速度为 gR,则物块在A点就离开轨道,不能沿着轨道运动到B
5
点,D错误。
故选AB。
9.BD
【详解】A.a、c两点间的电势差 W W +W -3.2×10-7+1.8×10-7
U = ac = ab bc = V=7V
ac q q -2×10-8
又U =φ -φ =φ -0=φ
ac a c a a
故φ =U =7V,故A错误;
a ac
BC.b、c两点间的电势差 W 1.8×10-7
U = bc = V=-9V
bc q -2×10-8
又U =φ -φ =φ -0=φ
bc b c b b
故φ =U =-9V,U =φ -φ =16V
b bc ab a b
将ab边平均分成16段,则每段的电势差为1V,在ab边上找到电势为0的d点,
9 9 9
则bd= ×ab= ×√52-32cm= cm
16 16 4
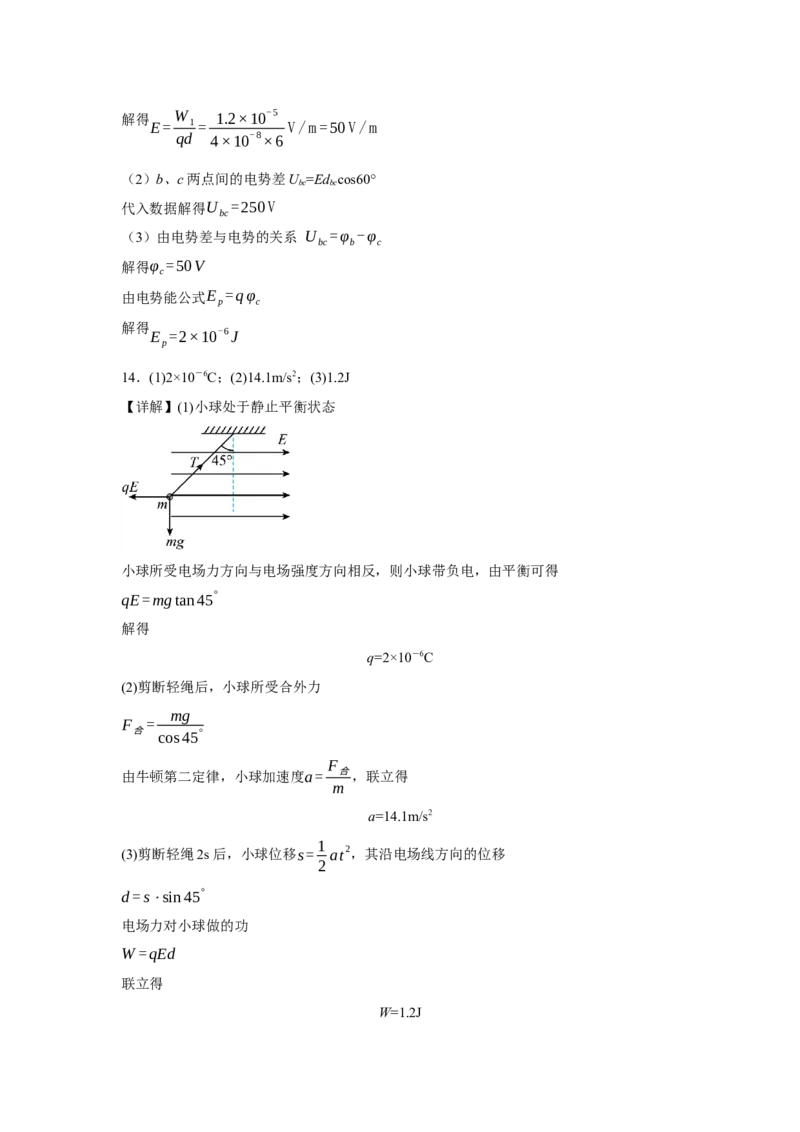
连接cd,并过b点作cd的垂线,垂足为e,则由e点指向b点的方向即为电场线的方向,
如图所示根据勾股定理,得
cd=√bc2+bd2=
√
32+
(9) 2
cm=
15
cm
4 4
9
则 bd 4 3
tan∠bcd= = =
bc 3 4
则∠bcd=37°,∠dbe=∠bcd=37°
3 9
又be=bc⋅sin37°=3× cm= cm
5 5
U 0-(-9)
E= db= V/m=500V/m
则电场强度大小 be 9 ,故B正确,C错误;
×10-2
5
φ +φ 7+0
D.ac中点的电势为φ= a c = V=3.5V
2 2
则该点电荷在ac中点的电势能 ,故D正确。
E =qφ=-2×10-8×3.5J=-7×10-8J
p
故选BD。
10.ACD
【详解】由图像知由点A运动到点B,电势降低,C对.斜率表示电势变化快慢,电势变
化越来越慢,场强变小,A对B错.负电荷在电势高出电势能低,电势能增加,D对.
11.(1) 3.205/3.204/3.206 5.015
(2)2.40
【详解】(1)[1]螺旋测微器的精确值为0.01mm,由图可知该金属丝的直径为
D=3mm+20.5×0.01mm=3.205mm
[2]20分度游标卡尺的精确值为0.05mm,由图可知该金属丝的长度为
L=5cm+3×0.05mm=50.15mm=5.015cm
(2)电压表的量程为0~3V,则分度值为0.1V,由图可知电压表的读数为2.40V。
12.(1) 变大 不变
(2)AC【详解】(1)[1]根据
εS
C=
4πkd
Q
C=
U
解得
4πkdQ
U=
εS
若把M板向左平移一小段距离后,电荷量Q不变,两极板的正对面积S也不变,增大两板
间距离d,两板间电压增大,静电计指针偏角增大;
[2]根据
4πkdQ
U=
εS
U
E=
d
解得
4πkQ
E=
εS
电场强度与两板间的距离无关,电场强度不变;
(2)A.实验中,通过分别改变电容器的结构,可以探究出影响平行板电容器电容的因素,
这种实验方法是控制变量法,A正确;
B.通过实验可以得出两极板之间的电压与极板的正对面积S、两极板间的距离d的关系,
不能得出平行板电容器的电容与极板的正对面积S成正比,与两极板间的距离d成反比的
结论,B错误;
Q
C.实验中极板上的电荷量几乎不变,根据电容器电容的定义式C= 可根据电压的变化判
U
定电容的变化,C正确;
故选AC。
13.(1)50V/m
(2)250V
(3)2×10-6J
【详解】(1)设a、b两点间距离为d,根据做功公式W =qEd
1解得 W 1.2×10-5
E= 1= V/m=50V/m
qd 4×10-8×6
(2)b、c两点间的电势差U =Ed cos60°
bc bc
代入数据解得U =250V
bc
(3)由电势差与电势的关系 U =φ -φ
bc b c
解得φ =50V
c
由电势能公式E =qφ
p c
解得
E =2×10-6J
p
14.(1)2×10-6C;(2)14.1m/s2;(3)1.2J
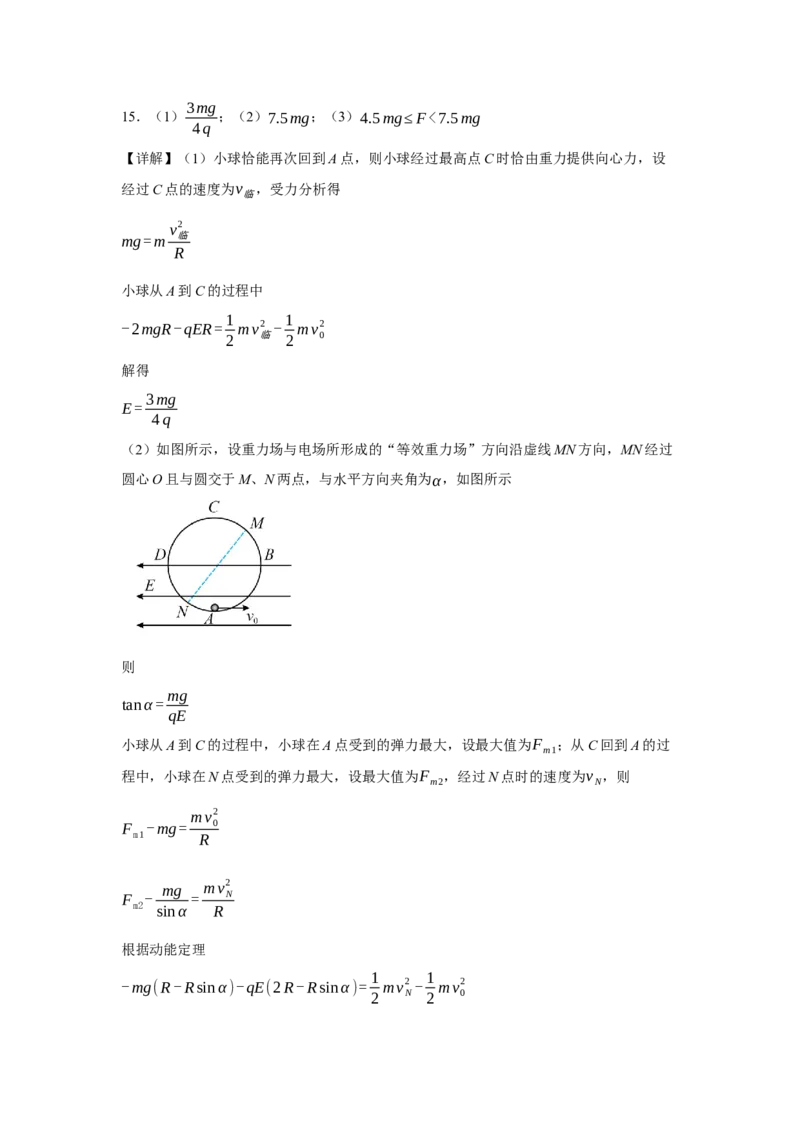
【详解】(1)小球处于静止平衡状态
小球所受电场力方向与电场强度方向相反,则小球带负电,由平衡可得
qE=mgtan45°
解得
q=2×10-6C
(2)剪断轻绳后,小球所受合外力
mg
F =
合 cos45°
F
由牛顿第二定律,小球加速度a= 合,联立得
m
a=14.1m/s2
1
(3)剪断轻绳2s后,小球位移s= at2,其沿电场线方向的位移
2
d=s⋅sin45°
电场力对小球做的功
W =qEd
联立得
W=1.2J3mg
15.(1) ;(2)7.5mg;(3)4.5mg≤F<7.5mg
4q
【详解】(1)小球恰能再次回到A点,则小球经过最高点C时恰由重力提供向心力,设
经过C点的速度为v ,受力分析得
临
v2
mg=m 临
R
小球从A到C的过程中
1 1
-2mgR-qER= mv2 - mv2
2 临 2 0
解得
3mg
E=
4q
(2)如图所示,设重力场与电场所形成的“等效重力场”方向沿虚线MN方向,MN经过
圆心O且与圆交于M、N两点,与水平方向夹角为α,如图所示
则
mg
tanα=
qE
小球从A到C的过程中,小球在A点受到的弹力最大,设最大值为F ;从C回到A的过
m1
程中,小球在N点受到的弹力最大,设最大值为F ,经过N点时的速度为v ,则
m2 N
mv2
F -mg= 0
m1 R
mg
mv2
F - = N
m2 sinα R
根据动能定理
1 1
-mg(R-Rsinα)-qE(2R-Rsinα)= mv2 - mv2
2 N 2 0解得
F =7.5mg
m1
F =5.25mg
m2
即弹力最大值
F =F =7.5mg
m m1
(3)若小球恰好完成一个完整的圆周运动到达A点,此后小球将脱离轨道。设小球脱离
轨道前,最后一次经过A点时最小速度为v ,轨道对小球弹力的最小值为F ,则
A1 1
1 1
mg⋅2R-qER= mv2 - mv2
2 A1 2 临
v2
F -mg=m A1
1 R
解得
F =4.5mg
1
由题意小球经过A点的速度为v 时,可恰好完成一个完整的圆周运动,则小球脱离轨道前
0
最后一次经过A点时的最大速度
v