文档内容
天津市部分区 2024~2025 学年度第一学期期中练习高三数学
本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,练习用时120分钟.
使用答题卡的地区,将答案写在答题卡上:不使用答题卡的地区,将答案写在练习卷上.
第Ⅰ卷(共45分)
注意事项:
本卷共9小题,每小题5分,共45分.
一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 设全集 ,集合 , ,则 ( )
A. B.
C. D.
2. 已知 , ,则 ( )
A. B. 1 C. D. 5
3. 若x, ,则“ 是“ ”的( )
A. 充分不必要条件 B. 必要不充分条件
.
C 充分必要条件 D. 既不充分也不必要条件
4. 已知等差数列 的前n项和为 ,若 ,则 ( )
A. 4 B. 3 C. 2 D. 1
5. 函数 的部分图象如下图所示,则 的解析式可能为( )
第1页/共7页
学科网(北京)股份有限公司A.
B.
C.
D.
6. 已知 ,则 ( )
A. B. C. D.
7. 已知 , , ,则a,b,c的大小关系为( )
A. B. C. D.
8. 已知函数 有极值点,则实数a的取值范围为( )
A. B. C. D.
9. 已知函数 在区间 上单调递增,且在区间 上有且仅有2个
零点,则 的取值范围为( )
A. B. C. D.
第Ⅱ卷
注意事项:
本卷共11小题,共105分.
二、填空题:本大题共6小题,每小题5分,共30分.试题中包含两个空的,答对1个的给3
分,全部答对的给5分.
第2页/共7页
学科网(北京)股份有限公司10. 若 为偶函数,则实数 ______.
.
11 已知函数 ,则 ______.
12. 若 ,且 ,则 的最小值为______.
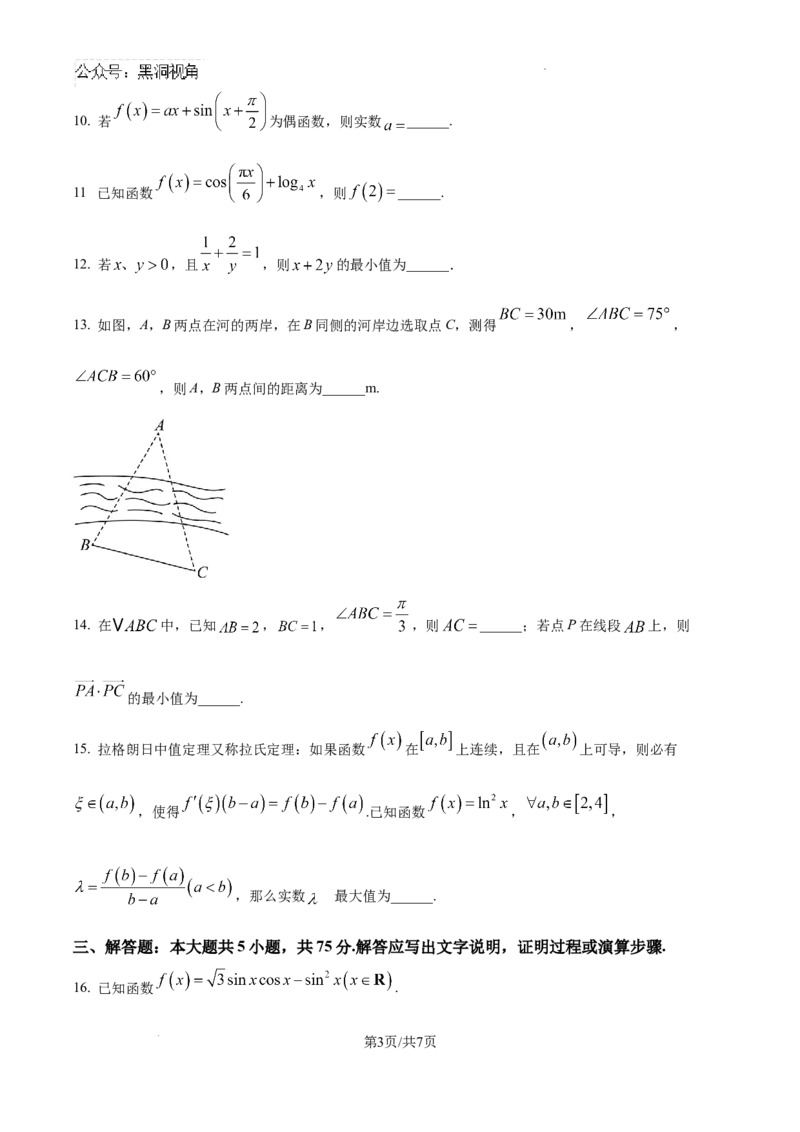
13. 如图,A,B两点在河的两岸,在B同侧的河岸边选取点C,测得 , ,
,则A,B两点间的距离为______m.
14. 在 中,已知 , , ,则 ______;若点P在线段 上,则
的最小值为______.
15. 拉格朗日中值定理又称拉氏定理:如果函数 在 上连续,且在 上可导,则必有
,使得 .已知函数 , ,
,那么实数 最的大值为______.
三、解答题:本大题共5小题,共75分.解答应写出文字说明,证明过程或演算步骤.
16. 已知函数 .
第3页/共7页
学科网(北京)股份有限公司(1)求 的最小正周期;
(2)求 在区间 上的最小值.
17. 已知 为等差数列, 为等比数列, , , , .
(1)求 和 通的项公式;
(2)求数列 的前n项和.
18. 在 中,角A,B,C的对边分别为a,b,c.已知 .
(1)求C的值;
(2)若 , ,求 的面积.
19. 已知函数 .
(1)若曲线 在点 处的切线的斜率为-3,求a的值;
的
(2)求 单调区间;
(3)若 ,对任意 , , ,不等式 恒成立,求实数k的取值
范围.
20. 已知数列 的前n项和为 , .
(1)求 的通项公式;
(2)设 ,求数列 的前n项和 ;
(3)证明:对于 中任意项 ,在 中都存在两项 , ,使得 .
第4页/共7页
学科网(北京)股份有限公司天津市部分区 2024~2025 学年度第一学期期中练习高三数学
本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,练习用时120分钟.
使用答题卡的地区,将答案写在答题卡上:不使用答题卡的地区,将答案写在练习卷上.
第Ⅰ卷(共45分)
注意事项:
本卷共9小题,每小题5分,共45分.
一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.
【1题答案】
【答案】C
【2题答案】
【答案】C
【3题答案】
【答案】B
【4题答案】
【答案】A
【5题答案】
【答案】A
【6题答案】
【答案】D
【7题答案】
【答案】C
【8题答案】
【答案】B
【9题答案】
【答案】D
第Ⅱ卷
注意事项:
本卷共11小题,共105分.
二、填空题:本大题共6小题,每小题5分,共30分.试题中包含两个空的,答对1个的给3
分,全部答对的给5分.
第5页/共7页
学科网(北京)股份有限公司【10题答案】
【答案】0
【11题答案】
【答案】1
【12题答案】
【答案】9
【13题答案】
【答案】
【14题答案】
【答案】 ①. ②.
【15题答案】
【答案】
三、解答题:本大题共5小题,共75分.解答应写出文字说明,证明过程或演算步骤.
【16题答案】
【答案】(1)
(2)
【17题答案】
【答案】(1) ,
(2) ,
【18题答案】
【答案】(1)
(2)
【19题答案】
第6页/共7页
学科网(北京)股份有限公司【答案】(1)
(2)答案见解析 (3)
【20题答案】
【答案】(1)
(2)
(3)证明见解析
第7页/共7页
学科网(北京)股份有限公司