文档内容
静海一中2024-2025第一学期高三数学(10月)
学生学业能力调研试卷
考生注意:
本试卷分第Ⅰ卷基础题(132分)和第Ⅱ卷提高题(15分)两部分,共
147分。3分卷面分。
知 识 技 能 学 习 能
力 ( 学
法)
内容 集 简 易 函 数 三 角 复数 导数与函数 平 面 向 不 等 关键环节
合 逻辑 性质 函数 量 式
分数 5 5 23 50 5 35 22 5 20
第Ⅰ卷 基础题(共132分)
一、选择题: 每小题5分,共45分.
1.已知集合 , 则 ( )
A. B. C. D.
2.已知 为正数,则“ ”是“ ”的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
3.函数 的部分图象大致为( )
A. B.
公众号:黑洞视角C. D.
4.已知函数 是定义在 上的偶函数,当 时, ,则使得
成立的 的取值范围是( )
A. B.
C. D.
5.已知 , , ,则( )
A. B.
C. D.
6.已知 ,则 ( )
A. B. C. D.
7.已知函数 , ,当 时,不等式 恒成
立,则实数a的取值范围为( )
A. B. C. D.
公众号:黑洞视角8.已知函数 的部分图象如图所示,则下列结论
正确的是( )
A. 的图象关于点 对称
B. 的图象向右平移 个单位后得到 的图象
C. 在区间 的最小值为
D. 为偶函数
9.如图,在平面四边形 中, , , ,
, , ,若点F为边AD上的动点,则 的最小值
为( )
公众号:黑洞视角A.1 B. C. D.2
二、填空题:每小题5分,共30分.
10.已知复数 ( 为虚数单位),其共轭复数为 ,则 的虚部为
.
11.计算: .
12.平面向量 , 满足 , , ,则 与 的夹角为
.
13.在∆ABC中,内角 的对边分别为 ,且 , , ,
则∆ABC的面积为 .
14.已知 ,且 ,则 的最小值为 .
15.在平面四边形 中, , ,若
→ → → →
AEDC AE⋅AF
,则2 ⋅ + = ;若 为边 上一动点,
公众号:黑洞视角→ →
PAPC
⋅
当 取最小值时,则 的值为 .
三、解答题:(本大题共5小题,共72分)
16.(15分)
在∆ABC中,内角 所对的边分别为 .已知 , , ,
.
(1)(5分)求 和 的值;
(2)(4分)求三角形BC边的中线 长;
(3)(6分)求 的值.
17.(12分)已知函数 , 的图象
的一个对称中心到最近的对称轴的距离为 .
(1)(5分)求函数 的单调递增区间:
(2)(7分)将函数 的图象上各点的横坐标缩短到原来的 ,纵坐标不变,得
到函数 的图象,求函数 在区间 上的值域.
18.(15分)设函数 .
(1)(4分)当 时,求 在 处的切线方程;
公众号:黑洞视角(2)(4分)讨论 的单调性;
(3)(7分)若 恒成立,求m的取值范围.
19.(15分)(1)(4分)设 ,对任意实数x,记
.若 有三个零点,则实数a的取值范围是
.
(2)(4分)已知函数 ,其中 ,若方程
有三个不同的实数根,则实数k的取值范围 .
(3)(4分)已知函数 ,函数 有四个零点,则
实数 的取值范围是 .
(4)(3分)问题:用数形结合法解决函数零点问题是常用的方法,请总结此方法使
用时需要注意什么问题?
第Ⅱ卷 提高题(共15分)
20.(15分)已知函数 , ( ).
(1)(4分)当 时,求曲线 在点 处的切线方程;
公众号:黑洞视角(2)(4分)求函数 的单调区间;
(3)(7分)若 对任意 恒成立,求整数a的最小值.
静海一中2024-2025第一学期高三数学(10月)
学生学业能力调研试卷答题纸
学校:
姓名:
班级:
考场:
座号
一、选择题:涂卡(不用做)
公众号:黑洞视角二、填空题(每题5分,共30分)
10. 11._________ 12.
13._______ 14.___________15.
三、解答题(本大题共5题,共72分)
16.(15分)
(1)(5分)
(2)(4分)
(3)(6分)
17.(12分)
(1)(5分)
(2)(7分)
公众号:黑洞视角18. (15分)
(1)(4分)
(2)(4分)
(3)(7分)
19.(15分)
(1)(4分)
公众号:黑洞视角(2)(4分)
(3)(4分)
(2)(3分)
20.(15分)
(1)(4分)
公众号:黑洞视角(2)(4分)
(3)(7分)
公众号:黑洞视角静海一中2024-2025第一学期高三数学(10月)
学生学业能力调研试卷 答案
一、选择题
题号 1 2 3 4 5 6 7 8 9
答案 D A A D A C B D B
二、填空题
10. 11.
12. 13. 14. 15. ,
三、解答题
16.(1)在 中,因为 ,故由 ,可得 .----1分
由已知及余弦定理,有 ,所以 .----3分
由正弦定理 ,得 .
所以, 的值为 , 的值为 .----5分
(2)设BC边的中点为D,在 中,
由余弦定理得:
公众号:黑洞视角,----9分
(3)由(1)及 ,得 ,所以 ,
.----12分
故 .----15分
17. (1)因为
,----2分
又由题 ,所以 ,
所以 ,
令 ,则 ,
所以函数 的单调递增区间为 .----5分
公众号:黑洞视角(2)由(1) ,
故由题意可得 ,----7分
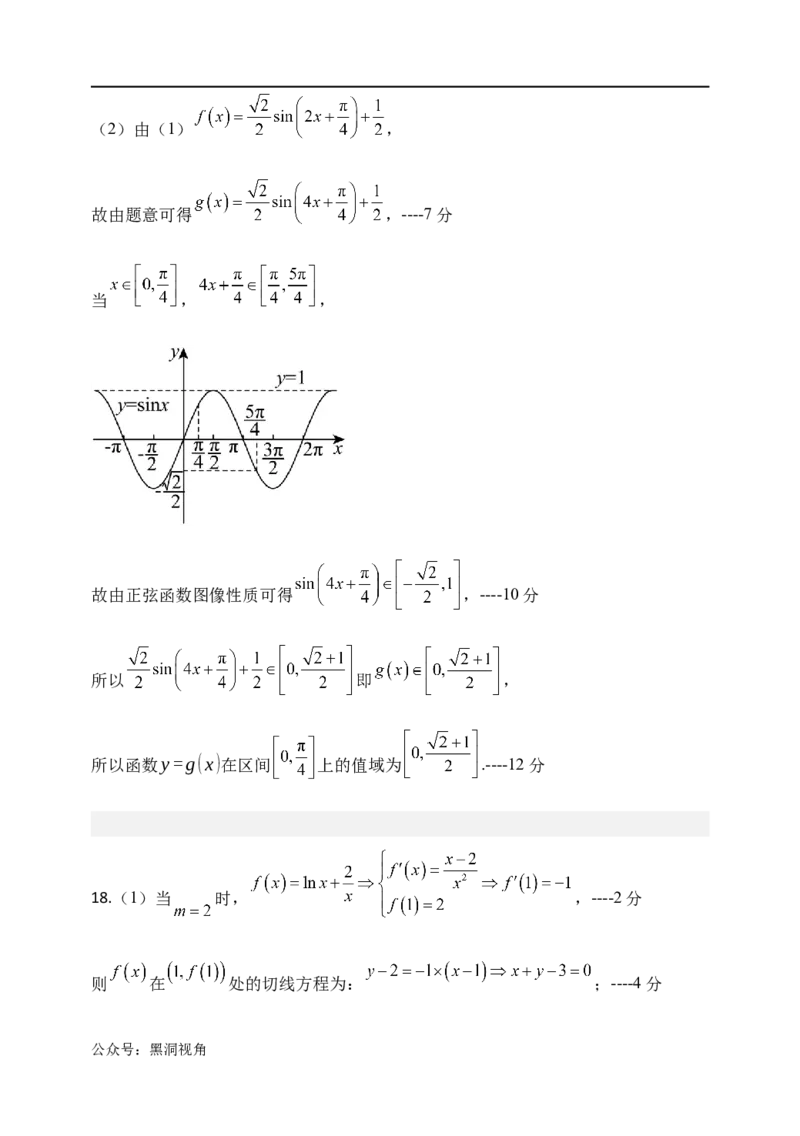
当 , ,
故由正弦函数图像性质可得 ,----10分
所以 即 ,
所以函数y=g(x)在区间 上的值域为 .----12分
18.(1)当 时, ,----2分
则 在 处的切线方程为: ;----4分
公众号:黑洞视角(2)由 ,
若 ,则 恒成立,即 在 上单调递增;
若 ,则 时,有 ,即 在 上单调递减,
时,有 ,即 在 上单调递减;
综上:若 时, 在 上单调递增;若 时, 在 上单调
递减;----8分
(3)不等式 恒成立,----11分
设 ,
易知 在 上单调递增,
又 ,所以 时有 , 时有 ,
即 在 上单调递减,在 上单调递增,----13分
所以 ,
故m的取值范围 .----15分
19. (1) ----4分
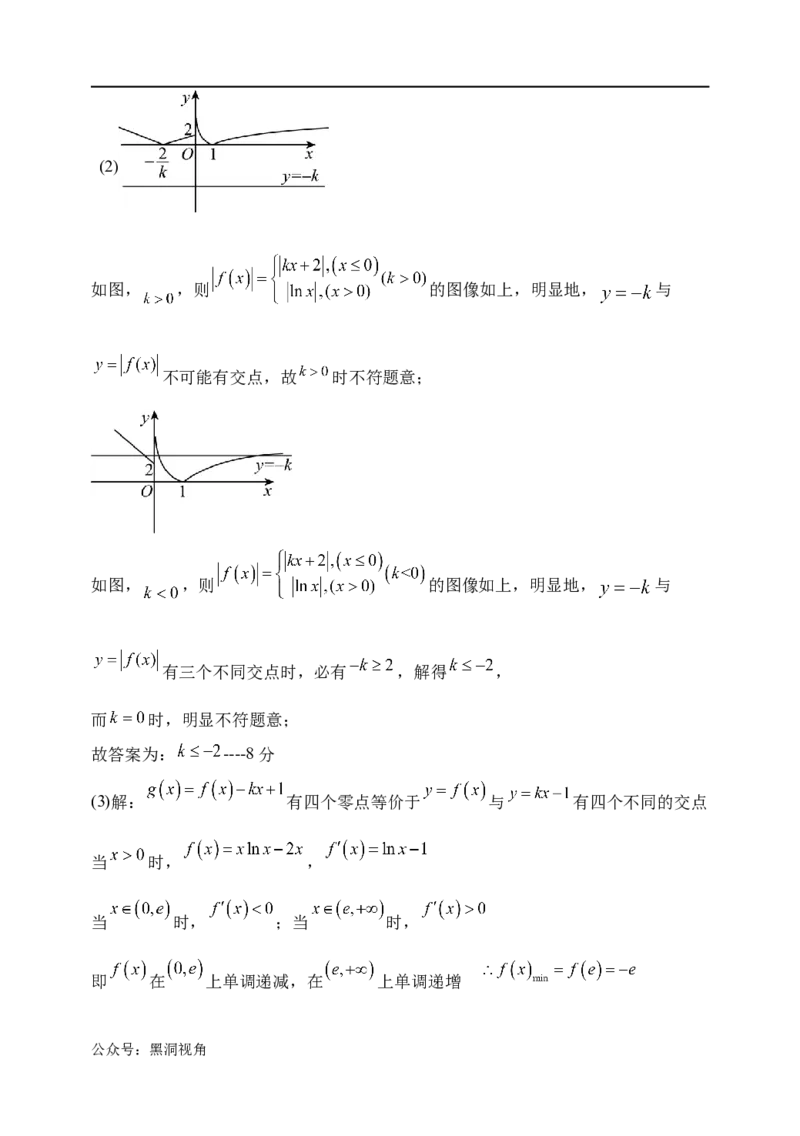
公众号:黑洞视角(2)
如图, ,则 的图像如上,明显地, 与
不可能有交点,故 时不符题意;
如图, ,则 的图像如上,明显地, 与
有三个不同交点时,必有 ,解得 ,
而 时,明显不符题意;
故答案为: ----8分
(3)解: 有四个零点等价于 与 有四个不同的交点
当 时, ,
当 时, ;当 时,
即 在 上单调递减,在 上单调递增
公众号:黑洞视角当 时, ,此时
由此可得 图象如下图所示:
恒过 ,由图象可知,直线位于图中阴影部分时,有四个不同交点
即临界状态为 与 两段图象分别相切
当 与 相切时,可得:
当 与 相切时
设切点坐标为 ,则
又 恒过 ,则
即 ,解得:
由图象可知: ----12分
20. 【详解】(1)当 时, ,
所以 ,
公众号:黑洞视角所以切线方程为 ,即 .----4分
(2)因为 ,
所以 ,----5分
设 ,
则 ,
又因为 ,所以 ,即 单调递增,
又因为 ,所以 时, ,即 ;
时, ,即 ,----7分
综上可知,函数 的单调递减区间为 ,单调递增区间为 .----8分
(3)因为 对任意 恒成,
即 , ,
即 ,
即 ,----11分
设 ,则 ,
公众号:黑洞视角易知 单调递增,所以 ,
所以 单调递增,则原不等式等价于 ,----13分
即 对任意 恒成立,
所以 ,令 ,则 ,
又因为 ,
令 ,则 ,所以 单调递减;
又因为 , ,
所以 ,
所以 时, ,即 , 单调递增;
时, ,即 , 单调递减;
所以 ,
所以 ,而 ,
所以整数 的最小值为 .----15分
公众号:黑洞视角公众号:黑洞视角