数学试卷_2024-2025高二（7-7月题库）_2024年12月试卷_1223浙江省丽水五校高中发展共同体期中高二2024-2025学年联考

绝密★考试结束前 学年第一学期丽水五校高中发展共同体期中联考 2024 高二年级数学学科 试题 考生须知： 1．本卷共4 页满分150分，考试时间120分钟。 2．答题前，在答题卷指定区域填写班级、姓名、考场号、座位号及准考证号并填涂相应数字。 3．所有答案必须写在答题纸上，写在试卷上无效。 4．考试结束后，只需上交答题纸。 选择题部分 一、选择题：本题共 8 小题，每小题 5 分，共 40 分. 在每小题给出的四个选项中， 只有一个选项是正确的．请把正确的选项填涂在答题卡相应的位置上. 1．直线 3x y30的倾斜角为( )    2 A． B． C． D． 4 6 3 3 2．已知空间向量a (m1,m,2),b(2,1,4),且a b，则m的值为( ) 10 10 A． B．10 C．10 D． 3 3 3．圆C :x2  y2 4与圆C :(x2)2 (y3)2 9的位置关系是( ) 1 2 A．内含 B．内切 C．外离 D．相交 y2 x2 4．已知双曲线  1的焦距为8，则该双曲线的渐近线方程为( ) m2 12 1 3 A．y x B．y3x C．y x D．y 3x 3 3 5．在正方体ABCD ABCD中，M 和N 分别为AB 和BB 的中点，那么直线AM 与CN 所成角的 1 1 1 1 1 1 1 余弦值是（ ） 2 2 21 21 A． B． C． D． 5 5 5 5 6．如图，太阳灶是一种将太阳光反射至一点用来加热水或食物的设备，上面装有抛物面形的反光镜， 镜的轴截面是抛物线的一部分，已知太阳灶的口径（直径）为4m，深度为0.5m，则该抛物线顶点 到焦点的距离为（ ） 高二数学学科 试题 第1页(共4页)A．0.25m B．0.5m C．1m D．2m x2 y2 7．已知椭圆C：  1,F,F 分别为其左右焦点，O为坐标原点，P为椭圆上一点，满足 9 5 1 2 1 cosFPF  ,则 OP 的长为（ ） 1 2 4 A． 6 B． 7 C．2 2 D． 31 8．已知AC 是棱长为8的正方体ABCD ABC D 的体对角线，空间一点M 满足MAMC 40， 1 1 1 1 1 1   AB是正方体的一条棱，则AM AB的最小值为（ ）         A．16 24 B．16 2 2 C．16 4 2 D．16 22 二、选择题：本题共 3 小题，每小题 6 分，共 18 分. 在每小题给出的选项中，有多 项符合题目要求. 全部选对得 6 分，部分选对的得部分分，选对但不全的得部分分， 有选错的得 0分.    9．已知a,b,c是空间中不共面的三个向量，则下列向量能构成空间的一个基底的是( )                     A．ab,c,abc B．a,2b,3c C．a,ab,c D．2abc,ab,ac 3 10．设O为坐标原点，直线y x1过抛物线C:y2 2px(p0)的焦点，且与C交于A,B两点， 3 l为C的准线，则（ ） A．p1 B．以AB为直径的圆与l相切 C． AB 8 D．S 4 △AOB 11．已知线段AB是圆C:(x1)2 (y3)2 4的一条动弦，|AB|2 3，直线l :mx y3m10与 1 直线l :xmy3m10相交于点P，下列说法正确的是( ) 2 A．直线l 恒过定点(3,1) B．直线l 与圆C恒相交 1 2 C．直线l ，l 的交点P在定圆x2  y2 4x2y0上 1 2 D．若G为AB中点 ，则PG 的最小值为4 5 高二数学学科 试题 第2页(共4页)非选择题部分 三、填空题：本题共 3 小题，每小题 5 分，共 15 分. 12．抛物线 y 4x2的准线方程为 ． 1 1 13．已知空间中三点A  2,2，0  ,B(0，, ),C(0，3，3),则点A到直线BC的距离为 ． 2 2 x2 y2 14．已知A,B,F分别是椭圆C：  1(a b0)的右顶点，上顶点和右焦点，若过A,B,F a2 b2 三点的圆恰与 y 轴相切，则C的离心率为 ． 四、解答题：本题共 5 小题，共 77 分. 解答应写出文字说明、证明过程或演算步骤. 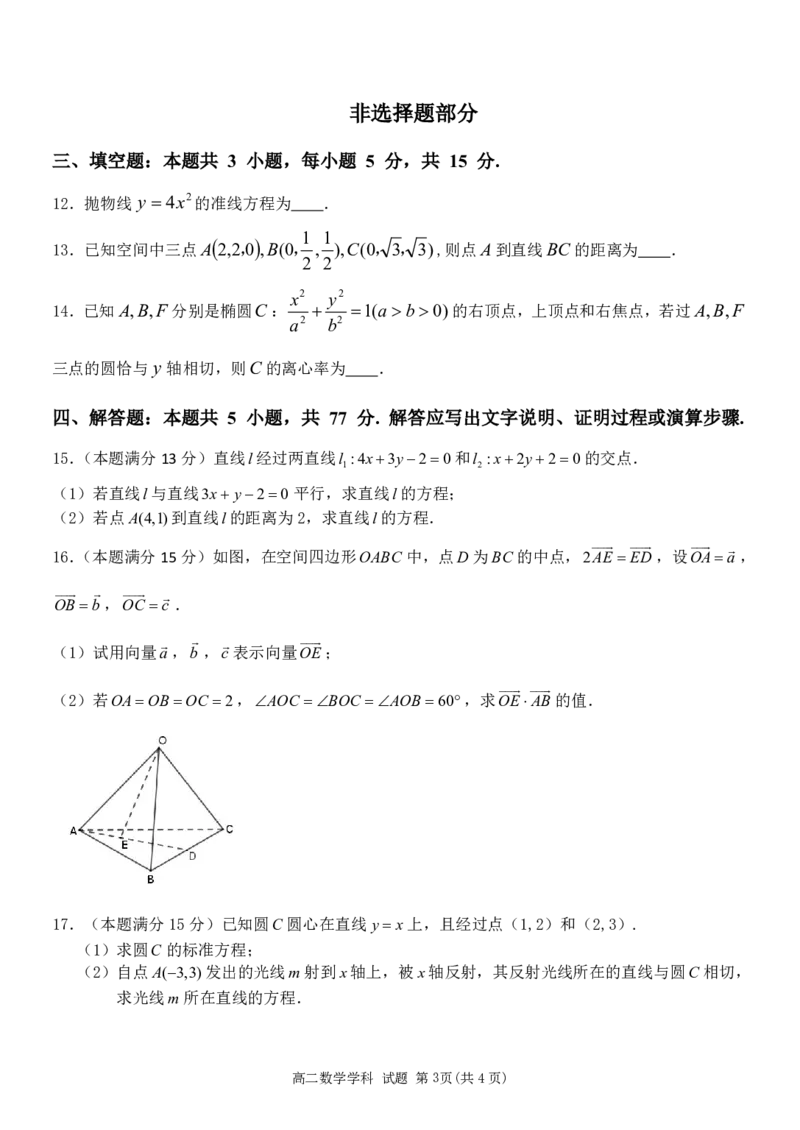15．（本题满分13分）直线l经过两直线l :4x3y20和l :x2y20的交点． 1 2 （1）若直线l与直线3x y20平行，求直线l的方程； （2）若点A(4,1)到直线l的距离为2，求直线l的方程．     16．（本题满分15分）如图，在空间四边形OABC 中，点D为BC的中点，2AE ED，设OAa，     OBb，OC c ．     （1）试用向量a，b ，c表示向量OE；   （2）若OAOBOC 2，AOC BOC AOB60，求OEAB的值． 17．（本题满分15分）已知圆C圆心在直线yx上，且经过点（1,2）和（2,3）. 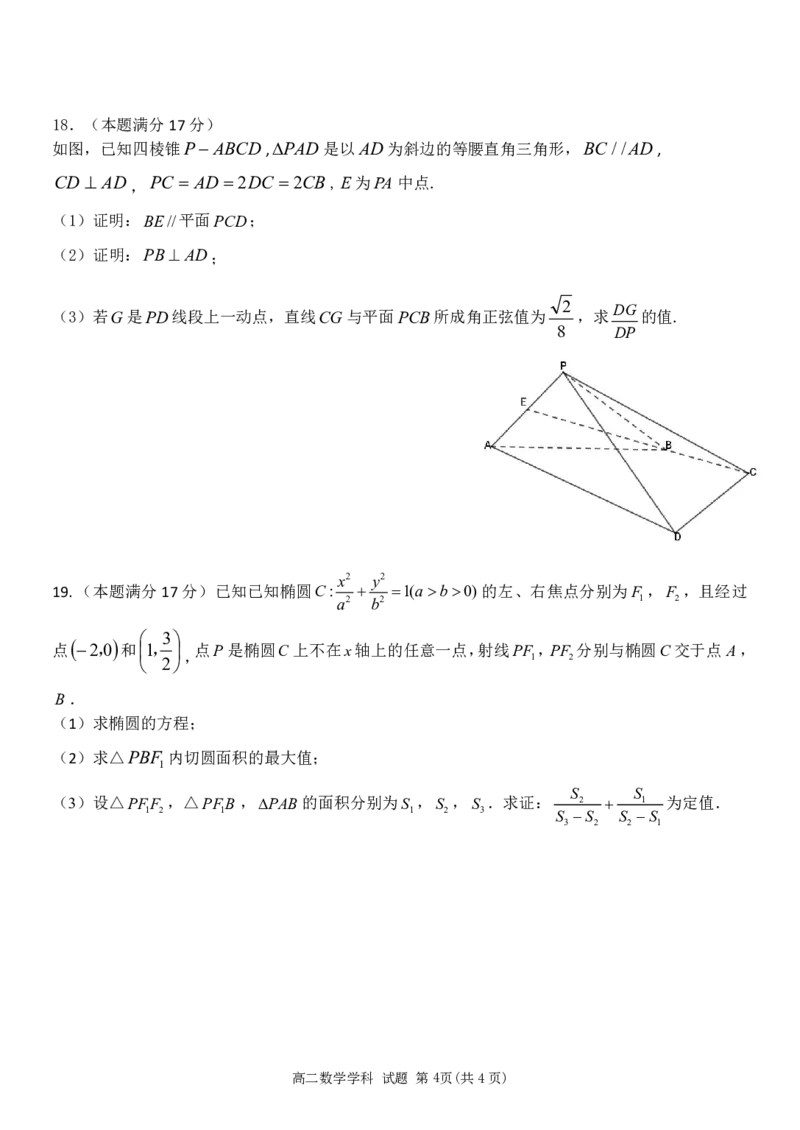（1）求圆C 的标准方程； （2）自点A(3,3)发出的光线m射到x轴上，被x轴反射，其反射光线所在的直线与圆C相切， 求光线m所在直线的方程． 高二数学学科 试题 第3页(共4页)18．（本题满分17分） 如图，已知四棱锥PABCD,PAD是以AD为斜边的等腰直角三角形，BC//AD, CD  AD，PC  AD 2DC 2CB,E为PA 中点. （1）证明：BE//平面PCD； （2）证明：PB AD； 2 DG （3）若G是PD线段上一动点，直线CG与平面PCB所成角正弦值为 ，求 的值. 8 DP x2 y2 19.（本题满分17分）已知已知椭圆C:  1(ab0)的左、右焦点分别为F ，F ，且经过 a2 b2 1 2  3 点  2，0  和  1， 2   ， 点P是椭圆C 上不在x轴上的任意一点，射线PF 1 ，PF 2 分别与椭圆C交于点A， B． （1）求椭圆的方程； （2）求△PBF 内切圆面积的最大值； 1 S S （3）设△PFF ，△PFB，PAB的面积分别为S ，S ，S ．求证： 2  1 为定值． 1 2 1 1 2 3 S S S S 3 2 2 1 声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布日期：2024/10/2915:36:34；用户：彭志凯；邮箱：suigao42@xyh.com；学号：30762996 高二数学学科 试题 第4页(共4页)