数学试卷_2024-2025高二（7-7月题库）_2024年12月试卷_1223浙江省金华市卓越联盟高二12月阶段性联考全科试卷及答案

2024 学年第一学期金华卓越联盟 12 月阶段性联考 高二年级数学试题 命题人：义乌三中 审题人：磐安二中 汤溪中学 考生须知： 1.本卷共4页满分150分，考试时间120分钟； 2.答题前，在答题卷指定区域填写班级､学号和姓名；考场号､座位号写在指定位置； 3.所有答案必须写在答题纸上，写在试卷上无效； 4.考试结束后，只需上交答题纸. 选择题部分 一､选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题 目的要求. x2 1.已知双曲线 y2 1的渐近线方程为（ ） 9 3 1 A. y x B.y   3x C. y 3x D. y x 3 3 2. 已知等差数列a ，前 n 项和为S ，若a 8, 则S （ ） n n 13 25 A．200 B．100 C．200 D．100 3. 直线xm1y10与直线mx2y10平行，则m的值为（ ） A．1或-2 B．1 C．-2 D． 2 4. 如果直线yxb与圆C:x2 y2 4相切，则b的值( ) A. 2 2 B. 2 2 C.2 2 D. 4 2 5. 空间直角坐标系oxyz中，定义经过点P  x ,y ,z 且法向量为m  (A,B,C) 的平面方程为 AxByCzD0  A,B,C,DR,A2 B2 C2 D2 0 ，平面外的一点Qx ,y ,z 到平面的距离 0 0 0 Ax By Cz D d  0 0 0 .阅读上面材料，解决下面问题：已知平面的方程为x2y2z20,在 A2 B2 C2 y 轴上求一点M使它到平面的距离为6，则点M的坐标为（ ） A.(0,8,0) B.(0,10,0) C.(0,10,0)或（0,8,0） D.(0,10,0)或（0,8,0） 高二数学学科 试题 第 1页（共4页）6.已知数列a 满足a 1,a a 2a a ，则数列a a 的前项和S 为（ ） n 1 n n1 n n1 n n1 n n n 1 2n A. B. C. D. 2n1 n1 n1 2n1 7. 在三棱台ABCABC 中，AB AC 2AA 2AB 4，BAA BAC CAA 600， 1 1 1 1 1 1 1 1 VABC 的重心为O，则AO的长为（ ） 1 1 1 10 3 3 A. 2 2 B. 5 C. D. 3 2 8.古希腊著名数学家阿波罗尼斯与欧几里得、阿基米德齐名，他发现：平面内到两个定点A,B的距 离之比为定值(1)的点所形成的图形是圆。后来，人们将这个圆以他的名字命名，称为阿波罗尼 斯圆，简称阿氏圆。已知点P,Q分别是抛物线C:x2 8y和E:x2  y2 12y320上的动点，若抛 物线C的焦点为F ，则2 PQ QF 的最小值为（ ） A．6 B．4 6 C．4 3 D．5 二､多选题：本题共3小题，每小题6分，共18分.在每小题给出的四个选项中，有多项是符合题目 要求的.全部选对的得6分，部分选对的得部分分，有选错的得0分. 9. 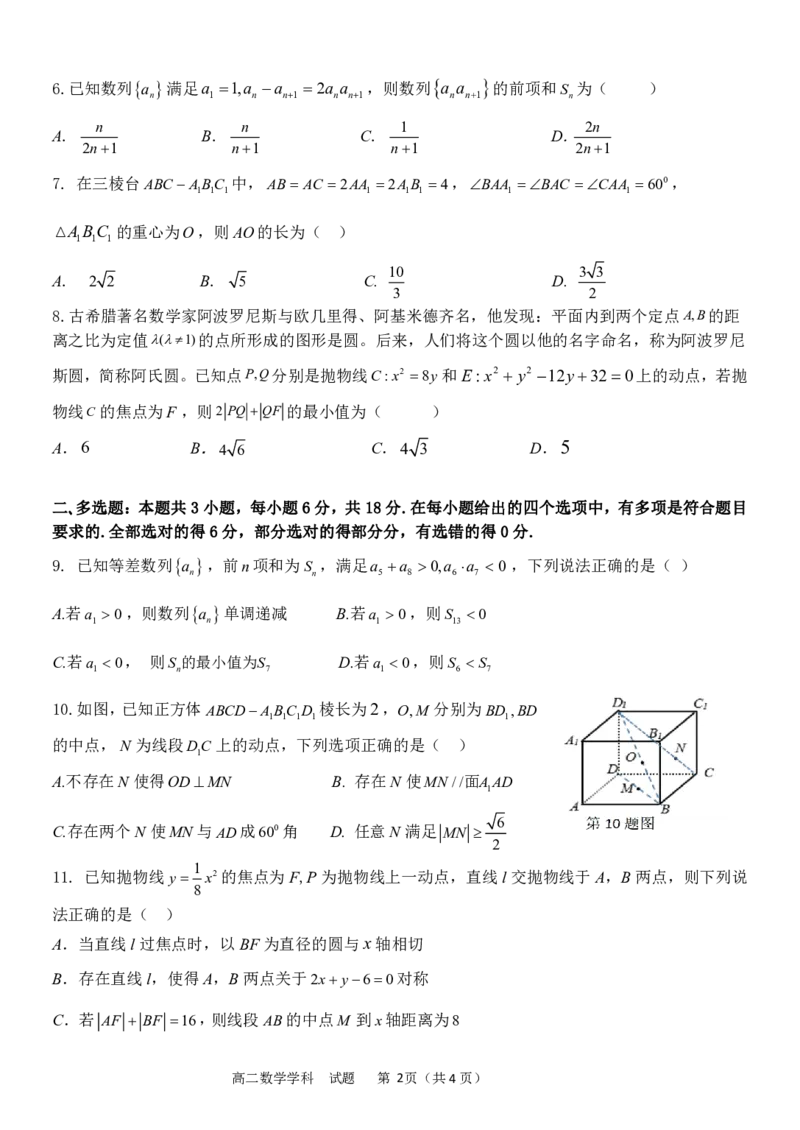已知等差数列a ，前n项和为S ，满足a a 0,a a 0 ，下列说法正确的是（ ） n n 5 8 6 7 A.若a 0，则数列a 单调递减 B.若a 0，则S 0 1 n 1 13 C.若a 0， 则S 的最小值为S D.若a 0，则S S 1 n 7 1 6 7 10.如图，已知正方体ABCDABC D 棱长为2，O,M 分别为BD ,BD 1 1 1 1 1 的中点，N 为线段DC上的动点，下列选项正确的是（ ） 1 A.不存在N 使得ODMN B. 存在N 使MN //面AAD 1 6 C.存在两个N 使MN与AD成600角 D. 任意N 满足 MN  2 1 11. 已知抛物线y x2的焦点为F,P为抛物线上一动点，直线l交抛物线于A，B两点，则下列说 8 法正确的是（ ） A．当直线l过焦点时，以BF为直径的圆与x轴相切 B．存在直线l，使得A，B两点关于2xy60对称 C．若 AF  BF 16，则线段AB的中点M 到x轴距离为8 高二数学学科 试题 第 2页（共4页）D．当直线l过焦点时，则2 AF 3BF 的最小值104 6 非选择题部分 三､填空题：本题共3小题，每题5分，共15分. 12.直线l的一个方向向量为( 3,1) ，则直线l的倾斜角为 . 13.如果数列a 对任意的nN*,a a a a ，则称a 为“速增数列”，若数列a 为“速增 n n2 n1 n1 n n n 数列”，且任意项a Z,a 1,a 3,a 211，则正整数k的最大值为 . n 1 2 k x2 y2 14.如图，已知双曲线C :  1(a0,b0) 与过其焦点的圆x2 y2 c2相交 1 a2 b2 于A,B,C,D四个点，直线AD与x轴交于点E，直线CE与双曲线C 交于点F， 1 记直线 AC,AF 的斜率分别为 k ,k ，若 k k 8 ，则双曲线 C 的离心率 1 2 1 2 1 为 . 四､解答题：本大题共5小题，共77分.解答应写出文字说明､证明过程或演算步骤. 15.(13分）已知圆C:x2  y2 2x4ym0被x轴截得的弦长为2 5，P 点是直线x y50上 的一点，过P 点作圆的两条切线，切点分别为A和B. （1）求m的值；（2）求四边形PACB面积的最小值. 16.(15分）已知递增等比数列a 的前n项和为S ，a 6,S 26,数列b 的前n项和为T ， n n 2 3 n n 2T  且b 1, n是公差为1的等差数列. 1  b  n （1）求数列a 和b 的通项公式；（2）令C a b ，求数列C 的前n项和K . 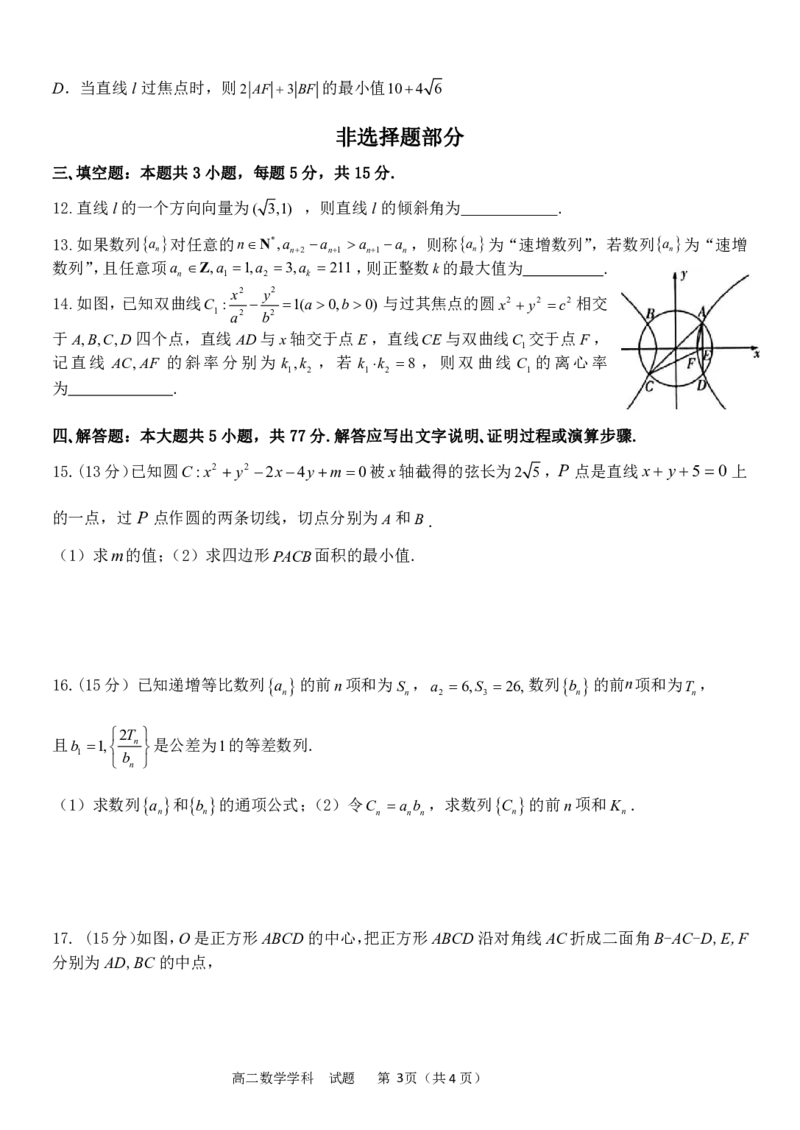n n n n n n n 17. (15分）如图，O是正方形ABCD的中心，把正方形ABCD沿对角线AC折成二面角B-AC-D,E,F 分别为AD,BC的中点， 高二数学学科 试题 第 3页（共4页）（1）当折成直二面角时(图1)，求直线OE与OF 所成角的大小； （2）当折成二面角BACD的平面角为600（图2），求直线BD与平面OEF所成角的正弦值. 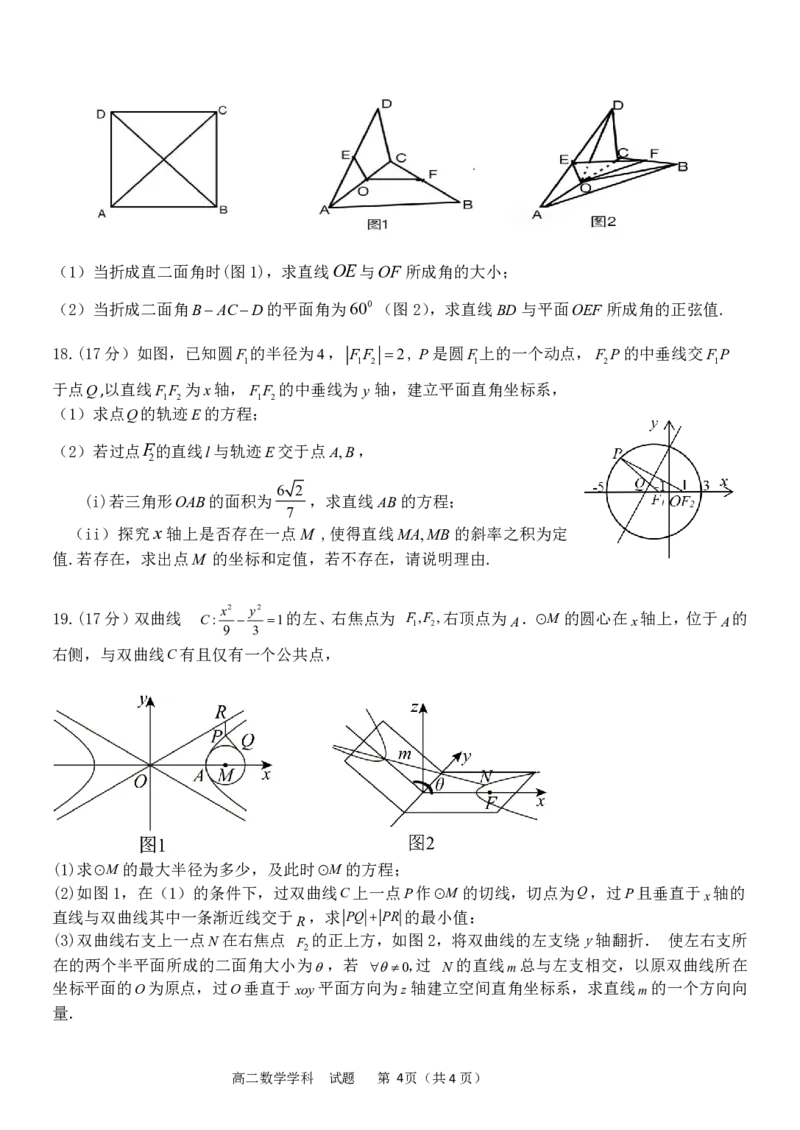18.(17分）如图，已知圆F的半径为4， FF 2,P是圆F上的一个动点，F P的中垂线交FP 1 1 2 1 2 1 于点Q,以直线FF 为x轴，FF 的中垂线为y轴，建立平面直角坐标系， 1 2 1 2 （1）求点Q的轨迹E的方程； （2）若过点F的直线l与轨迹E交于点A,B， 2 6 2 (i)若三角形OAB的面积为 ，求直线AB的方程； 7 （ii）探究x轴上是否存在一点M ,使得直线MA,MB的斜率之积为定 值.若存在，求出点M 的坐标和定值，若不存在，请说明理由. x2 y2 19.(17分）双曲线 C:  1的左、右焦点为 F 1 ,F 2 ,右顶点为 A ．M 的圆心在 x 轴上，位于 A 的 9 3 右侧，与双曲线C有且仅有一个公共点， (1)求M 的最大半径为多少，及此时M 的方程； (2)如图1，在（1）的条件下，过双曲线C上一点P作M 的切线，切点为Q，过P且垂直于 x 轴的 直线与双曲线其中一条渐近线交于 R ，求 PQ  PR 的最小值： (3)双曲线右支上一点N在右焦点 F 的正上方，如图2，将双曲线的左支绕y轴翻折． 使左右支所 2 在的两个半平面所成的二面角大小为，若 0，过 N的直线 m 总与左支相交，以原双曲线所在 坐标平面的O为原点，过O垂直于xoy平面方向为 z 轴建立空间直角坐标系，求直线 m 的一个方向向 量． 高二数学学科 试题 第 4页（共4页）