期中试卷答案_2024-2025高二（7-7月题库）_2024年11月试卷_1130浙江省宁波市余姚中学2024-2025学年高二上学期期中考试

余姚中学 2024学年第一学期高二上期中数学试题 一、选择题: 本大题共 8 小题, 每小题 5 分, 共 40 分. 每小题给出的四个选项中, 只有一 选项是正确的，请把正确的选项填涂在答题卡相应的位置上. 𝑥2 𝑦2 1.𝑀是双曲线 − =1上一点，点𝐹 ，𝐹 分别是双曲线的左、右焦点，若|𝑀𝐹 |=5，则 1 2 1 4 12 |𝑀𝐹 |= ( ) 2 A. 9或1 B. 1 C. 9 D. 9或2 【答案】C 【解析】【分析】本题考查双曲线的性质，考查运算求解能力，属于中档题． 根据双曲线的定义即可求解结论． 𝑥2 𝑦2 𝑎2 =4, 𝑎 =2, 【解答】解：由 − =1，得{ 所以{ 4 12 𝑐2 =𝑎2+𝑏2 =16, 𝑐 =4, 由双曲线的定义可知||𝑀𝐹 |−|𝑀𝐹 ||=2𝑎 =4，所以|𝑀𝐹 |=1或9，又|𝑀𝐹 |≥𝑐−𝑎 =2， 1 2 2 2 所以|𝑀𝐹 |=9． 2 故选C． 2.在各项均为正数的等比数列{𝑎 }中，𝑎 =2𝑎 +3𝑎 ，若存在两项𝑎 ，𝑎 使得√ 𝑎 𝑎 =3𝑎 ， 𝑛 6 5 4 𝑚 𝑘 𝑚 𝑘 1 1 4 则 + 的最小值为 ( ) 𝑚 𝑘 7 5 9 A. B. C. D. 2 3 2 4 【答案】A 【解析】【分析】 本题考查了等比数列的性质，属于简单题 本题先求出该等比数列的公比，再将后式化简，得出𝑚和𝑘的关系，即可求解 【解答】 设等比数列{𝑎 }的公比为𝑞(𝑞 >0)， 因为𝑎 =2𝑎 +3𝑎 ，所以𝑞2 =2𝑞+3，即𝑞2−2𝑞− 𝑛 6 5 4 3=0，解得𝑞 =3或𝑞 =−1(舍去).因为√ 𝑎 𝑎 =3𝑎 ，所以𝑎 𝑎 =9𝑎2，即𝑎2⋅3𝑚+𝑘−2 = 𝑚 𝑘 1 𝑚 𝑘 1 1 9𝑎2，所以𝑚+𝑘 =4， 所以{ 𝑚 =1, 或{ 𝑚 =2, 或{ 𝑚 =3, 所以 1 + 4 的值为 7 或 5 或 13 ，所以 1 𝑘 =3 𝑘 =2 𝑘 =1, 𝑚 𝑘 3 2 3 1 4 7 + 的最小值为 .故选A． 𝑚 𝑘 33．若动点P(x,y)满足方程 ( x + 2 ) 2 + y 2 − ( x − 2 ) 2 + y 2 = 3 ，则动点P的轨迹方程为 （ ） A． x9 4 2 − y7 4 2 = 1 B． x9 4 2 + y7 4 2 = 1 C． x 8 2 + y 4 2 = 1 D． x 1 2 6 − y 1 2 2 = 1 解析：由题意得点P(x,y)到点A(−2,0)与点 B ( 2 , 0 ) 的距离之差的绝对值为3，且43， 故动点P的轨迹方程是以A(−2,0)与 B ( 2 , 0 ) 为焦点的双曲线，故2a=3,c=2，所以 a = 3 2 , b 2 = c 2 − a 2 = 4 − 9 4 = 7 4 x2 y2 − =1 ，所以双曲线的方程为 9 7 .故选：A. 4 4 4．阅读材料: 在空间直角坐标系 O x y z 中, 过点 P ( x 0 , y 0 , z 0 ) 且一个法向量为n=(a,b,c) 的平面的方程为 a ( x − x 0 ) + b ( y − y 0 ) + c ( z − z 0 ) = 0 . 阅读上面材料,解决下面问题: 已知平面的方程为2x− y+z =2, 点M(−1,2,1), 则点M 到平面的距离为（ ） A. 5 1 1 0 0 2 2 B. 1 3 0 4 2 C. 5 6 6 D. 6 6 [解] 因为平面  的方程为 2x− y+z =2, 所以平面 的一个法向量为 n=(2,−1,1), 在平面  上任取一点 A(1, 1,1), 则 MA=(2,−1,0), 所以点 M 到 平面  的距离 d = |MAn| 5 5 6 = = . 故选 C. |n| 6 6 5. 已知直四棱柱 A B C D − A 1 B 1 C 1 D 1 的底面 A B − CD为矩形, A B = 1 , B C = 3 ,且 1 CM = MB ,若点B到平面 1 2 1 A B 1 D 1 2 的距离为 , 则点C到直线AM 的距离为（ ） 2 A. 30 B. 3 2 0 C. 5 D. 2 [解] 以D为原点, 建立如图所示的空间直角坐标系，连接 A C ，由题得 A(3,0,0),B(3,1,0),C(0,1,0), 令DD =a(a0), 则D(0,0,a),B(3,1, a),M(1, 1 1 1 1,a),AD =(−3,0,a),AB =(0,1,a), 设平面ABD 的法向 1 1 1 1量为n=(x,y,z), 则  n n   A A D B 1 1 = = − y 3 + x a + z a = z 0 = , 0 , 令 z = 3 , 得n=(a,−3a,3). 而 A B = ( 0 , 1 , 0 ) , 由点 B 2 |nAB| 3a 2 到平面ABD 的距离为 , 得 = = , 1 1 2 |n| 10a2 +9 2 3 2  3 2   3 2  解得a= ,于是M 1,1, ,AM =−2,1, , 而     4 4 4     A C = ( − 3 , 1 , 0 ) ,则 | A C | A  M A M | | = ( | − − 2 2 )  2 + ( − 1 3 2 ) + +  1 3  4 1 2 |  2 = 2 2 , 所以点 C 到直线AM 的距离为 | A C 2| − ( 2 2 ) 2 = 1 0 − 8 = 2 . 故选 D . 6. 长方体 A B C D − A B C 1 D 1 ， A B = B C = 1 ， B B 1 = 2 ，动点 P 满足 B P B C B B 1 ( , [ 0 ,1 ] )    = +  ， A P ⊥ B D 1 ，则二面角 P − A D − B 的正切值的取值范围是（ ） A．  0 , 1 4   1 B． 0, C．    2  1 4 , 1 2  1  D． ,1   2  【详解】 以 D 为原点，分别以DA,DC,DD 所在直线为x,y,z轴建立空间直角坐标系. 1 已知AB=BC=1， B B 1 = 2 ，则A(1,0,0)，B(1,1,0)， B 1 (1 ,1 , 2 ) , D 1 ( 0 , 0 , 2 ) ， D ( 0 , 0 , 0 ) , C ( 0 ,1 , 0 ) . 因为BP=BC+BB(,[0,1])，所以 1 BP=BC+BB =(−1,0,0)+(0,0,2)=(−,0,2), 1A P A B B P ( 0 ,1 , 0 ) ( , 0 , 2 ) ( ,1 , 2 )     = + = + − = − , B D 1 = ( − 1 , − 1 , 2 ) 因为AP⊥BD，所以 1 A P B D 1 1 4 0    = − + = ,因为[0,1],1−40,1，所以 0 , 1 4     ， 设平面 A D B 的法向量为 n 1 = ( 0 , 0 ,1 ) ，设平面 A D P 的法向量为 n 2 = ( x 2 , y 2 , z 2 ) ， D A = (1 , 0 , 0 ) ， A P ( ,1 , 2 )   = − .由  n n 2 2   D A A P = = 0 0 ，即 x 2 x 2 0 y 2 2 z 2 0    − = + + = ，令 x 2 = 0 ，则 y 2 2  = ，z =−1， 2 则n =(0,2,−1)为平面 2 A D P 的一个法向量.设二面角 P − A D − B 为，由图可知为锐角， 所以 c o s n n 1 1 n n 2 2  =  . n 1 n 2 0 0 0 2 1 ( 1 ) 1   =  +  +  − = − . n 1 = 1 ， | n 2 | 0 2 ( 1 ) 2 4 2 4 2 1   = + − + = + .所以 c o s 1 1 4 2 , s in 1 1 1 4 2 1 4 4 2 2 ,       = + = − + = + 则 ta n 2 0 , 1 2   =    .则二面角 P − A D − B 的正切值的取值范围是  0 , 1 2  故选：B. 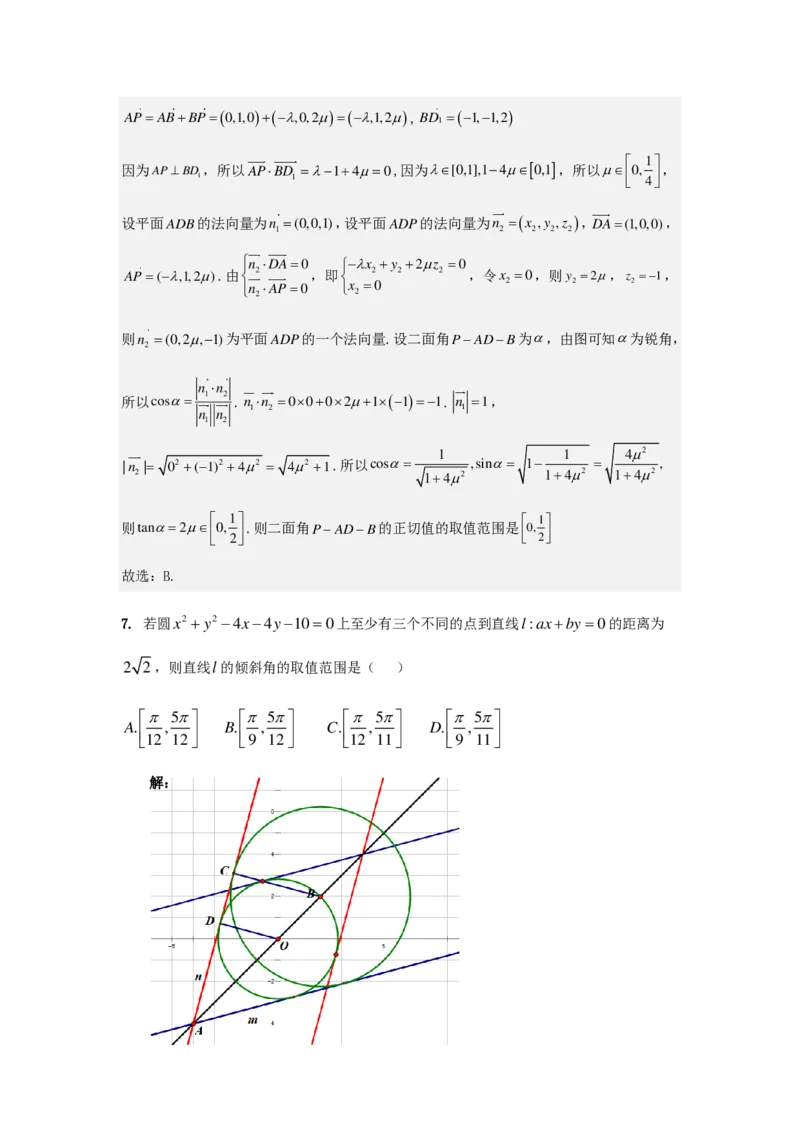7. 若圆 x 2 + y 2 − 4 x − 4 y − 1 0 = 0 上至少有三个不同的点到直线l:ax+by =0的距离为 2 2 ，则直线 l 的倾斜角的取值范围是（ ） A . 1 2 , 5 1 2      5 B. ,   9 12 C . 1 2 , 5 1 1     D . 9 , 5 1 1     解：为使得圆 x 2 + y 2 − 4 x − 4 y − 1 0 = 0 上至少有三个不同的点到直线 l : a x + b y = 0 的距 离为 2 2 ，只要圆 x 2 + y 2 = 8 的两条平行切线与圆 x 2 + y 2 − 4 x − 4 y − 1 0 = 0 都相交或者 一条与圆相交，另一条与圆相切。因此，由蓝色的两条平行切线转到红色的两条平行切线的 过程中都是满足题意的。为此所求直线 l 的倾斜角取值范围即为蓝色直线 m 的倾斜角与红色 直线 n 的倾斜角之间。 由于已知圆的圆心B(2,2)，半径为 3 2 ，于是直线 O B 为y = x，倾斜角为 4  ， BC =3 2 。又OD=2 2。由三角形AOD与三角形  A B C 相似知OA=4 2，故 O A D 6   = ，直线 m 的倾斜角为 4 6 1 2    − = ，直线 n 的倾斜角为 4 6 5 1 2    + = 。因此， 直线 l 的倾斜角的取值范围是 1 2 , 5 1 2     。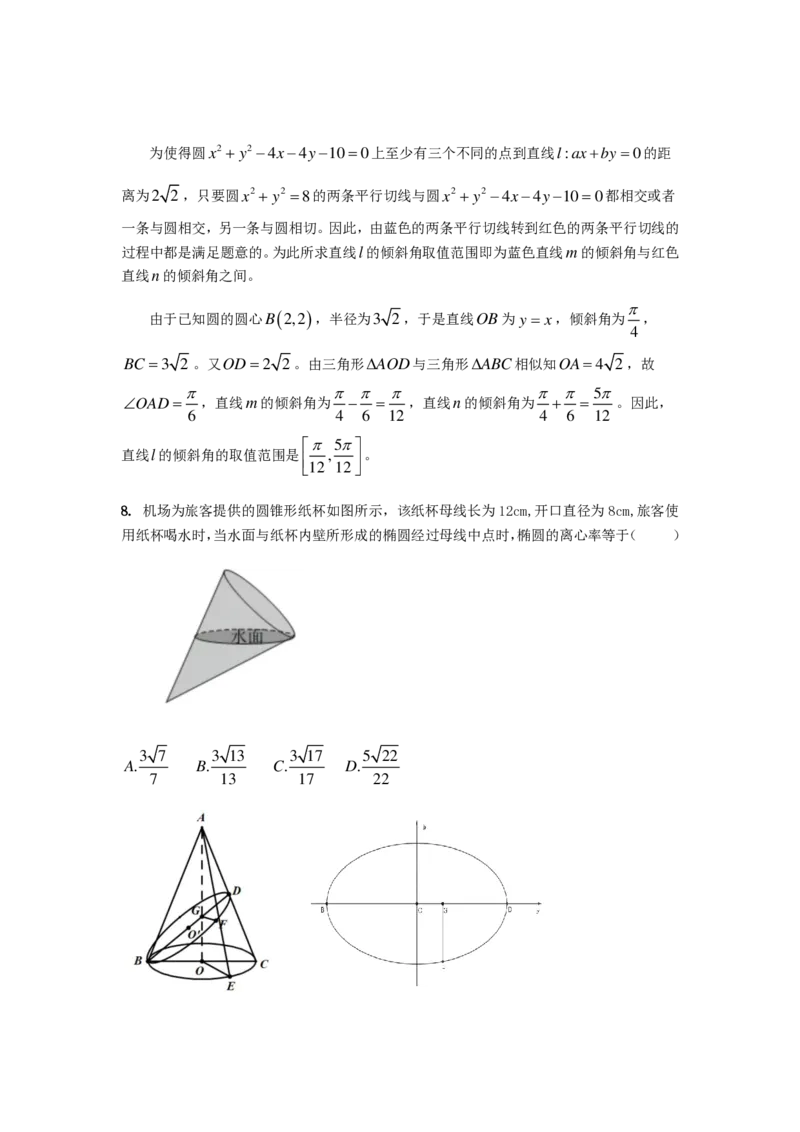 8. 机场为旅客提供的圆锥形纸杯如图所示，该纸杯母线长为12cm,开口直径为8cm,旅客使 用纸杯喝水时，当水面与纸杯内壁所形成的椭圆经过母线中点时，椭圆的离心率等于（ ） A . 3 7 7 3 13 B. 13 C . 3 1 1 7 7 D . 5 2 2 2 2解法： D 是母线 A C 的中点， B D 是中线，又 A O 也是中线，设 A O  B D = G ， 则G是  A B C 重心，设 B D 的中点为 O ' ，即椭圆的中心，设 BD =2a, O 'G = a 3 , G D = 2 3 a , 作平面 A O E ⊥ 平面ABC，  A G F  A O E ， G O F E = A A G O = 2 3 , G F = 8 3 . 对椭 圆如图建系， F  a 3 , − 8 3  , 故  a 3 a 2 2 +  − b 8 32  2 = 1 , b 2 = 8 , 根据平行四边形的性质，知 2 ( 8 2 + 1 2 2 ) = ( 4 a ) 2 + 1 2 2 , a = 1 7 , 于是， c 2 = a 2 − b 2 = 1 7 − 8 = 9 , c = 3 , e = c a = 3 1 7 = 3 1 1 7 7 . 二、选择题: 本大题共 3 小题, 每小题 6 分, 共计18分。每小题给出的四个选项中, 有多 项符合题目要求,。全部选对得 6分, 选对但不全的得部分分，有选错的得 0 分。 9.(多选题)已知曲线𝐶：𝑎𝑥2+𝑎𝑦2−2𝑥+4𝑎2𝑦=0，下列结论正确的是 ( ) A. 当𝑎 =0时，曲线𝐶是一条直线 B. 当𝑎 ≠0时，曲线𝐶是一个圆 C. 当曲线𝐶是圆时，它的面积的最小值为2𝜋 D. 当曲线𝐶是面积为5𝜋的圆时，|𝑎|=1 【答案】AB 【解析】【分析】 本题考查圆的方程，以及圆的面积，考查方程思想和运算能力，属于中档题． 由𝑎 =0，可得曲线为𝑥 =0，可判断𝐴;由𝑎 ≠0，化曲线𝐶为圆的标准方程，求得半径，由基 本不等式可得最小值，可判断𝐵𝐶;由半径为√ 5，解方程可得𝑎，可判断𝐷． 【解答】 解：对于𝐴选项，当𝑎 =0时，曲线𝐶的方程为𝑥 =0，此时曲线𝐶是一条直线，A正确； 对于𝐵选项，当𝑎 ≠0时，曲线𝐶的方程可化为𝑥2+𝑦2− 2 𝑥+4𝑎𝑦=0，因为(− 2 ) 2 +16𝑎2 = 𝑎 𝑎 4 +16𝑎2 >0，所以曲线𝐶是一个圆，B正确； 𝑎2 √ 4 +16𝑎2 对于𝐶选项，当曲线𝐶是圆时，其半径𝑟 = 𝑎2 =√ 4𝑎2+ 1 ≥√ 2√ 4𝑎2⋅ 1 =2，当且 2 𝑎2 𝑎2仅当4𝑎2 = 1 ，即𝑎 =± √ 2 时，等号成立，即𝑟的最小值为2，因此，当曲线𝐶是圆时，它的 𝑎2 2 面积的最小值为𝜋×22 =4𝜋，C错误； 对于𝐷选项，当曲线𝐶是面积为5𝜋的圆时，其半径𝑟 =√ 4𝑎2+ 1 =√ 5，即4𝑎2+ 1 =5， 𝑎2 𝑎2 1 解得𝑎 =±1或𝑎 =± ， D错误． 2 故选AB． 𝑥2 𝑦2 10.(多选题)已知椭圆𝐶： + =1的左、右焦点分别为𝐹 ，𝐹 ，点𝑃是椭圆上的一个动点， 1 2 4 3 则以下说法正确的是 ( ) A. △𝐹 𝑃𝐹 的周长为6 1 2 B. 若∠𝐹 𝑃𝐹 =60°，则△𝐹 𝑃𝐹 的面积为√ 3 1 2 1 2 C. 椭圆𝐶上存在两个点𝑃，使得∠𝐹 𝑃𝐹 =90° 1 2 1 2 9 D. + 的最小值为 2|𝑃𝐹1| |𝑃𝐹2| 8 【答案】ABD 【解析】由 𝑥2 + 𝑦2 =1，得𝑎2 =4，𝑏2 =3，则𝑐2 =1，所以𝑎 =2，𝑐 =1，因为点𝑃是椭圆 4 3 上的一个动点，所以|𝑃𝐹 |+|𝑃𝐹 |=2𝑎=4.对于𝐴，△𝐹 𝑃𝐹 的周长为|𝑃𝐹 |+|𝑃𝐹 |+ 1 2 1 2 1 2 |𝐹 𝐹 |=2𝑎+2𝑐 =6，故A正确；对于𝐵，在△𝐹 𝑃𝐹 中，由余弦定理得|𝐹 𝐹 |2 =|𝑃𝐹 |2+ 1 2 1 2 1 2 1 |𝑃𝐹 |2−2|𝑃𝐹 ||𝑃𝐹 |cos∠𝐹 𝑃𝐹 ，即|𝐹 𝐹 |2 =(|𝑃𝐹 |+|𝑃𝐹 |)2−3|𝑃𝐹 ||𝑃𝐹 |，则4=16− 2 1 2 1 2 1 2 1 2 1 2 1 3|𝑃𝐹 ||𝑃𝐹 |，所以|𝑃𝐹 ||𝑃𝐹 |=4，所以△𝐹 𝑃𝐹 的面积为 |𝑃𝐹 ||𝑃𝐹 |sin∠𝐹 𝑃𝐹 =√ 3，故 B 1 2 1 2 1 2 1 2 1 2 2 正确；对于𝐶，当点𝑃位于椭圆的短轴端点处时，∠𝐹 𝑃𝐹 最大，此时|𝑃𝐹 |=|𝑃𝐹 |=2=|𝐹 𝐹 |， 1 2 1 2 1 2 则△𝐹 𝑃𝐹 为等边三角形，故∠𝐹 𝑃𝐹 的最大值为60°，所以椭圆𝐶上不存在点𝑃，使得∠𝐹 𝑃𝐹 = 1 2 1 2 1 2 1 2 1 1 90°，故C错误；对于𝐷，因为|𝑃𝐹 |+|𝑃𝐹 |=2𝑎 =4，所以 + = ( + 1 2 2|𝑃𝐹1| |𝑃𝐹2| 4 2|𝑃𝐹1| 2 )(|𝑃𝐹 |+|𝑃𝐹 |)= 1 ( 5 + |𝑃𝐹2| + 2|𝑃𝐹1| )≥ 1 ( 5 +2√ |𝑃𝐹2| ⋅ 2|𝑃𝐹1| )= 9 ，当且仅当|𝑃𝐹 |= 1 2 2 |𝑃𝐹2| 4 2 2|𝑃𝐹1| |𝑃𝐹2| 4 2 2|𝑃𝐹1| |𝑃𝐹2| 8 8 1 2 9 2|𝑃𝐹 |= 时，取等号，经检验符合题意，所以 + 的最小值为 ，故 D正确．故选 1 3 2|𝑃𝐹1| |𝑃𝐹2| 8 ABD． 11.|𝑥|+|𝑦|称为点𝑃(𝑥，𝑦)的“𝛿和”，下列说法正确的是 ( ) A. “𝛿和”为1的点𝑃(𝑥，𝑦)的轨迹围成的图形的面积为2 B. 设𝑃是直线2𝑥−𝑦−4=0上任意一点，则点𝑃(𝑥，𝑦)的“𝛿和”的最小值为2C. 设𝑃是直线𝑎𝑥−𝑦+2=0上任意一点，则使得“𝛿和”最小的点有无数个的充要条件是 𝑎 =1 D. 设𝑃是椭圆𝑥2+ 𝑦2 =1上任意一点，则“𝛿和”的最大值为√ 3 2 【答案】ABD 【解析】对于𝐴，由“𝛿和”的定义得|𝑥|+|𝑦|=1，作出图形如图所示，根据图形得到四边 形𝐴𝐵𝐶𝐷为边长是√ 2的正方形，其面积为2，故A正确；对于𝐵，∵点𝑃是直线2𝑥−𝑦−4=0 4−3𝑥,𝑥 ≤0, 上任意一点，∴𝑦 =2𝑥−4，则|𝑥|+|𝑦|=|𝑥|+|2𝑥−4|={4−𝑥,0<𝑥 <2,可知当𝑥 =2时， 3𝑥−4,𝑥 ≥2, |𝑥|+|𝑦|取到最小值2，故B正确；对于𝐶，∵点𝑃是直线𝑎𝑥−𝑦+2=0上任意一点，∴𝑦 =𝑎𝑥+ 2，则|𝑥|+|𝑦|=|𝑥|+|𝑎𝑥+2|，可知当𝑎 =±1时，都满足使得“𝛿和”最小的点有无数个， 故C错误；对于𝐷，可设𝑃(cos𝜃,√ 2sin𝜃)，则|𝑥|+|𝑦|=|cos𝜃|+|√ 2sin𝜃|，易知其最大值 为√ 3，故 D正确．故选ABD． 三、填空题: 本大题共 3小题, 每小题 5 分, 共 15分。 12.已知数列{𝑎 }的前𝑛项和𝑆 =3𝑛−2，则𝑎 =__________． 𝑛 𝑛 𝑛 1,𝑛 =1, 【答案】{ 2×3𝑛−1,𝑛 ≥2 【解析】【分析】本题主要考查由数列前𝑛项和公式推导数列的通项公式，属于基础题， 先算出𝑛 =1时𝑎 ，再根据𝑛 ≥2时，𝑎 =𝑆 −𝑆 即可求得结论. 1 𝑛 𝑛 𝑛−1 【解答】 解：因为数列{𝑎 }的前𝑛项和𝑆 =3𝑛−2， 𝑛 𝑛 所以𝑎 =𝑆 =3−2=1， 1 1 当𝑛 ≥2时，𝑎 =𝑆 −𝑆 =3𝑛−3𝑛−1 =2×3𝑛−1， 𝑛 𝑛 𝑛−1又𝑎 =1不满足上式， 1 1,𝑛 =1, 所以𝑎 ={ 𝑛 2×3𝑛−1,𝑛 ≥2. 13.如图，两个正方形𝐴𝐵𝐶𝐷，𝐶𝐷𝐸𝐹的边长都是2，且二面角𝐴−𝐶𝐷−𝐸的大小为60°，𝑀， 𝑁为对角线𝐴𝐶和𝐹𝐷上的动点，且满足𝐴𝑀 =𝐹𝑁，则线段𝑀𝑁长度的最小值 为 ． 【答案】 2√ 5 5 【解析】【分析】本题主要考查二面角概念的应用，考查向量数量积概念的应用，属于中档 题， ∠𝐴𝐷𝐸即为二面角𝐴−𝐶𝐷−𝐸的平面角，以𝐷⃗⃗⃗⃗𝐴⃗ ,𝐷⃗⃗⃗⃗𝐶⃗ ,𝐷⃗⃗⃗⃗𝐸⃗ 为基底表示𝑀⃗⃗⃗⃗⃗⃗𝑁⃗ 即可得解． 【解答】 解：由题意知，𝐷𝐴=𝐷𝐶 =𝐷𝐸 =2，且𝐷𝐴⊥𝐷𝐶，𝐷𝐸 ⊥𝐷𝐶， 所以∠𝐴𝐷𝐸即为二面角𝐴−𝐶𝐷−𝐸的平面角，则∠𝐴𝐷𝐸 =60°． 因为𝐴𝑀 =𝐹𝑁，𝐴𝐶 =𝐷𝐹，设𝐴𝑀 =𝜆𝐴𝐶，0≤𝜆 ≤1， 所以𝐷𝑁 =𝐷𝐹−𝐹𝑁 =(1−𝜆)𝐷𝐹， 则𝑀⃗⃗⃗⃗⃗𝑁⃗⃗ =𝑀⃗⃗⃗⃗⃗𝐴⃗ +𝐴⃗⃗⃗⃗⃗𝐷⃗ +𝐷⃗⃗⃗⃗𝑁⃗⃗ =−𝜆𝐴⃗⃗⃗⃗𝐶⃗ −𝐷⃗⃗⃗⃗𝐴⃗ +(1−𝜆)𝐷⃗⃗⃗⃗𝐹⃗ =(𝜆−1)𝐷⃗⃗⃗⃗𝐴⃗ −(2𝜆−1)𝐷⃗⃗⃗⃗𝐶⃗ −(𝜆− 2 1)𝐷⃗⃗⃗⃗⃗𝐸⃗ ，则𝑀⃗⃗⃗⃗⃗𝑁⃗⃗ =[(𝜆−1)𝐷⃗⃗⃗⃗𝐴⃗ −(2𝜆−1)𝐷⃗⃗⃗⃗𝐶⃗ −(𝜆−1)𝐷⃗⃗⃗⃗⃗𝐸⃗ ]2 =4(𝜆−1)2+4(2𝜆−1)2+4(𝜆−1)2−4(𝜆−1)2 =20𝜆2−24𝜆+8=20(𝜆− 3 ) 2 + 4 ，故 5 5 当𝜆 = 3 时，𝑀⃗⃗⃗⃗⃗𝑁⃗⃗ 2 取得最小值 4 ， 5 5 所以|𝑀⃗⃗⃗⃗⃗𝑁⃗⃗ |≥ 2√ 5 ，所以线段𝑀𝑁长度的最小值为 2√ 5 ． 5 5 x2 y2 14.已知双曲线C: − =1(a0,b0),若双曲线不存在以点 a2 b2 ( 2 a , a ) 为中点的弦，则双曲 线离心率e的取值范围是 。解： 0  ( 2 a a 2 ) 2 − a b 2 2  1 , 3  a b 2 2  4 , e = a 2 + a 2 b 2 = 1 + b a 2 2   2 5 , 2 3 3  . 四、解答题: 本大题共 5 小题, 共 77 分。解答应写出文字说明、证明过程或演算步骤。 3．在等差数列 { a n } 中， a 3 = 7 , a 9 = − 5 , { a n } 的前n项和为 S n ． (1)求数列 { a n } 的通项公式； (2)求 S n 取最大值时 n 的值； (3)设 T n = | a 1 | + | a 2 | + | a 3 | +  + | a n | ，求T ． n 【详解】（1）由题意知在等差数列 { a n } 中，a =7,a =−5，设公差为d， 3 9 则a −a =6d =−12d =−2，则 9 3 a 1 = a 3 − 2 d = 1 1 ， 故a =a +(n−1)d =13−2n，故通项公式 n 1 a n = 1 3 − 2 n ． n(n−1) （2）结合（1）可得S =11n+ (−2)=12n−n2 =−(n−6)2+36， n 2  当 n = 6 时， S n 取最大值． （3） a n = 1 3 − 2 n ，  由 1 3 − 2 n  0 ，得 n  1 3 2 = 6 1 2 ， 即n6时有a 0， n n  7 时有a 0， n 若n6， T n = | a 1 | + | a 2 | + | a 3 | +  + | a n |= a 1 + a 2 + a 3 +  + a n = S n = 1 2 n − n 2 ， 若n7时，T =a +a ++a −a −−a n 1 2 6 7 n = 2 ( a 1 + a 2 +  + a 6 ) − ( a 1 + a 2 + a 3 +  + a n ) = 2 S 6 − S n = 2 (1 2  6 − 3 6 ) − (1 2 n − n 2 ) = n 2 − 1 2 n + 7 2 ，综合上述 T n =  1 n 2 2 n − − 1 n 2 2 n , n +  7 2 6 , , n n   7 N , n   N  ． 16. 已知数列{𝑎 }满足𝑎 =3，𝑎 =2𝑎 −2． 𝑛 1 𝑛+1 𝑛 (1)求证：{𝑎 −2}为等比数列； 𝑛 (2)求数列{𝑛𝑎 }的前𝑛项和𝑆 ． 𝑛 𝑛 【答案】解：(1)证明：由𝑎 =2𝑎 −2， 𝑛+1 𝑛 得𝑎 −2=2𝑎 −4=2(𝑎 −2)， 𝑛+1 𝑛 𝑛 又𝑎 −2=1， 1 所以{𝑎 −2}是以1为首项，2为公比的等比数列． 𝑛 (2)由(1)知𝑎 −2=2𝑛−1，故𝑎 =2+2𝑛−1， 𝑛 𝑛 则𝑛𝑎 =2𝑛+𝑛×2𝑛−1． 𝑛 设数列{𝑛·2𝑛−1}的前𝑛项和为𝑇 ， 𝑛 则𝑇 =1×20+2×21+3×22+⋯+𝑛×2𝑛−1， 𝑛 2𝑇 =1×21+2×22+3×23+⋯+𝑛×2𝑛， 𝑛 两式相减得 −𝑇 =1+21+22+23+⋯+2𝑛−1−𝑛×2𝑛 𝑛 =2𝑛−1−𝑛×2𝑛， 所以𝑇 =(𝑛−1)2𝑛+1， 𝑛 故𝑆 =2(1+2+3+⋯+𝑛)+𝑇 𝑛 𝑛 𝑛(𝑛+1) =2× +𝑇 2 𝑛 =𝑛(𝑛+1)+(𝑛−1)2𝑛+1． 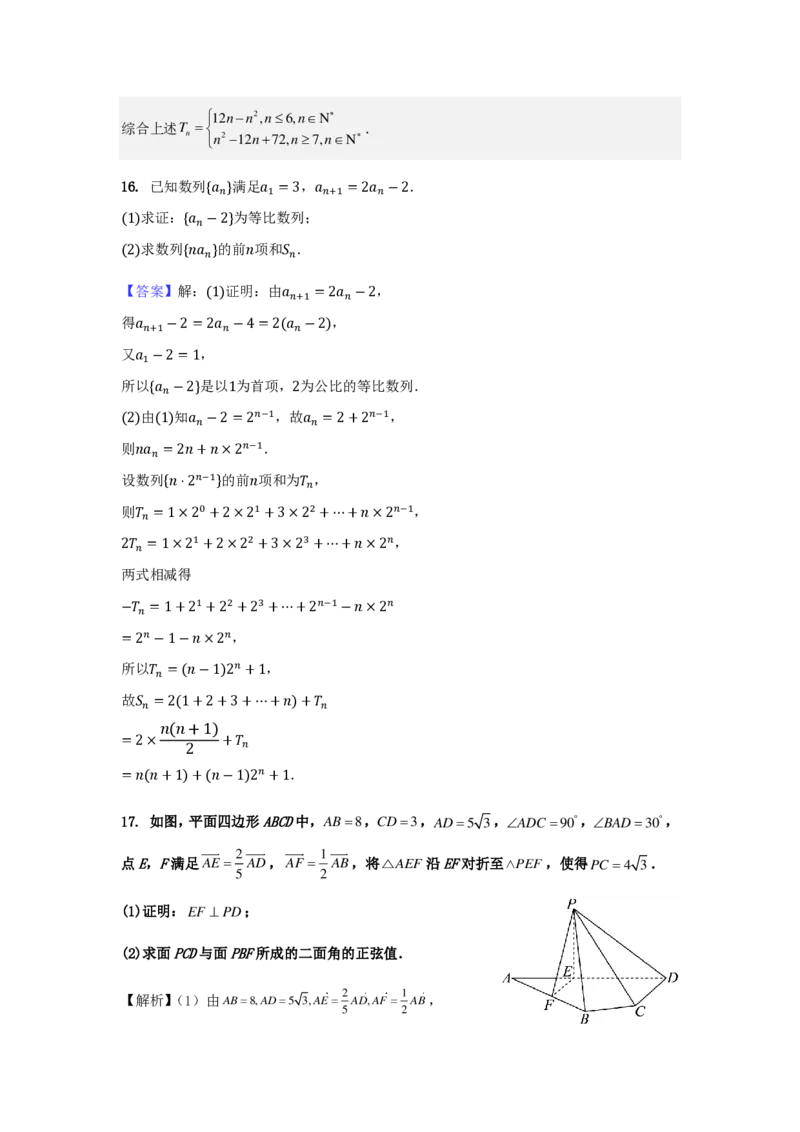17. 如图，平面四边形ABCD中， A B = 8 ， C D = 3 ，AD=5 3，  A D C = 9 0  ，BAD=30， 2 点E，F满足AE= AD， 5 A F = 1 2 A B ，将 △ A E F 沿EF对折至 PEF，使得 P C = 4 3 ． (1)证明：EF ⊥PD； (2)求面PCD与面PBF所成的二面角的正弦值． 2 1 【解析】（1）由AB=8,AD=5 3,AE= AD,AF= AB， 5 2得AE=2 3,AF =4，又  B A D = 3 0  ，在△AEF 中， 由余弦定理得 E F = A E 2 + A F 2 − 2 A E  A F c o s  B A D = 1 6 + 1 2 − 2  4  2 3  3 2 = 2 , 所以 A E 2 + E F 2 = A F 2 ，则 A E ⊥ E F ，即 E F A D ⊥ ， 所以 E F ⊥ P E , E F ⊥ D E ，又 P E D E = E , P E 、 D E  平面 P D E ， 所以 E F ⊥平面 P D E ，又 P D  平面 P D E ， 故EF⊥ P D ； （2）连接 C E ，由ADC=90,ED=3 3,CD=3，则 C E 2 = E D 2 + C D 2 = 3 6 ， 在 P E C 中， P C = 4 3 , P E = 2 3 , E C = 6 ，得 E C 2 + P E 2 = P C 2 ， 所以 P E ⊥ E C ，由（1）知 P E ⊥ E F ，又 E C E F = E , E C 、 E F  平面 A B C D ， 所以 P E ⊥ 平面 A B C D ，又ED平面 A B C D ， 所以 P E ⊥ E D ，则 P E , E F , E D 两两垂直，建立如图空间直角坐标系 E − x y z ， 则E(0,0,0),P(0,0,2 3),D(0,3 3,0),C(3,3 3,0),F(2,0,0),A(0,−2 3,0)， 由 F 是AB的中点，得B(4,2 3,0)， 所以 P C = (3 , 3 3 , − 2 3 ), P D = ( 0 , 3 3 , − 2 3 ), P B = ( 4 , 2 3 , − 2 3 ), P F = ( 2 , 0 , − 2 3 ) ， 设平面 P C D 和平面 P B F 的一个法向量分别为n=(x,y,z ),m=(x ,y ,z )， 1 1 1 2 2 2  nPC =3x +3 3y −2 3z =0 则 1 1 1 ， nPD=3 3y −2 3z =0 1 1  m m   P P B F = = 4 2 x x 2 2 + − 2 2 3 3 y z 2 2 − = 2 0 3 z 2 = 0 ， 令y =2,x = 3，得 1 2 x 1 = 0 , z 1 = 3 , y 2 = − 1 , z 2 = 1 ， 所以n=(0,2,3),m=( 3,−1,1)， mn 1 65 所以 cosm,n = = = ， m n 5 13 65 8 65 设平面PCD和平面PBF所成角为，则sin= 1−cos2= ， 65即平面 P C D 和平面 P B F 所成角的正弦值为 8 6 6 5 5 . 18.已知𝐹是抛物线𝐶:𝑦2 =2𝑝𝑥(𝑝>0)的焦点，𝐴是𝐶上在第一象限的一点，点𝐵在𝑦轴上， 𝐴𝐵 ⊥𝑦轴，|𝐴𝐵|=2，|𝐴𝐹|=3． (1)求𝐶的方程； (2)过𝐹作斜率为𝑘的直线与𝐶交于𝑀，𝑁两点，▵𝑀𝑂𝑁的面积为√ 5(𝑂为坐标原点)，求直线𝑀𝑁 的方程． 【答案】解：(1)由题知，𝑥 =2， 𝐴 𝑝 𝑝 由抛物线的定义知，|𝐴𝐹|=𝑥 + =2+ =3， 𝐴 2 2 ∴𝑝 =2，∴𝐶的方程为𝑦2 =4𝑥． (2)由(1)知𝐹(1,0)，设𝑀(𝑥 ,𝑦 )，𝑁(𝑥 ,𝑦 )， 1 1 2 2 直线𝑀𝑁的方程为𝑦=𝑘(𝑥−1)， 代入𝑦2 =4𝑥，整理得𝑘2𝑥2−(2𝑘2+4)𝑥+𝑘2 =0， 2 2𝑘 +4 由题易知𝑘 ≠0，∴𝑥 +𝑥 = ，𝑥 𝑥 =1， 1 2 2 1 2 𝑘 ∴|𝑀𝑁|=√ 1+𝑘2|𝑥 −𝑥 | 1 2 =√ (1+𝑘2)[(𝑥 +𝑥 )2−4𝑥 𝑥 ] 1 2 1 2 2 2 2𝑘 +4 4(1+𝑘 ) =√ (1+𝑘2)[( )2−4×1]= ， 2 2 𝑘 𝑘 |𝑘| ∵𝑂到直线𝑀𝑁的距离为𝑑 = ， √ 1+𝑘 2 1 1 4(1+𝑘 2 ) |𝑘| 2√ 1+𝑘 2 ∴𝑆 = |𝑀𝑁|⋅𝑑 = × × = =√ 5，解得𝑘 =±2， ▵𝑀𝑂𝑁 2 2 𝑘 2 √ 1+𝑘 2 |𝑘| ∴直线𝑀𝑁的方程为𝑦 =2𝑥−2或𝑦 =−2𝑥+2．19.(本小题15分) 已知平面上的动点𝑀(𝑥，𝑦)与定点(1,0)之间的距离和动点𝑀到定直线𝑥 =2的距离的比是常 数√ 2 ，记动点𝑀的轨迹为曲线𝐶，直线𝑙与曲线𝐶交于𝑃(𝑥 ，𝑦 )，𝑄(𝑥 ，𝑦 )两个不同的点，𝑂 1 1 2 2 2 为坐标原点． (1)若直线𝑙的方程为𝑦 =2𝑥+2，求△𝑂𝑃𝑄的面积； (2)若△𝑂𝑃𝑄的面积为√ 2 ，证明：𝑥2+𝑥2和𝑦2+𝑦2均为定值． 2 1 2 1 2 【答案】解：(1)由题意可知√ (𝑥−1)2+𝑦2 = √ 2 |𝑥−2|，化简得 𝑥2 +𝑦2 =1，即曲线𝐶的 2 2 𝑦=2𝑥+2, 方程为 𝑥 2 2 +𝑦2 =1. 由{ 𝑥2 +𝑦2 =1 消去𝑦，得9𝑥2+16𝑥+6=0，则𝛥 =40>0，且𝑥 1 + 2 16 2 𝑥 =− ，𝑥 𝑥 = ，所以|𝑃𝑄|=√ 1+4×√ (𝑥 +𝑥 )2−4𝑥 𝑥 =√ 5× 2 1 2 1 2 1 2 9 3 √ (− 16 ) 2 −4× 2 = 10√ 2 ，又坐标原点𝑂到直线𝑃𝑄的距离𝑑 = 2 = 2√ 5 ， 所以△𝑂𝑃𝑄的 9 3 9 √ 12+22 5 面积𝑆 = 1 ×|𝑃𝑄|×𝑑 = 1 × 10√ 2 × 2√ 5 = 2√ 10 ． 2 2 9 5 9 (2)证明：当直线𝑙的斜率不存在时， 设直线𝑙的方程为𝑥 =𝑡，将𝑥 =𝑡代入 𝑥2 +𝑦2 =1， 2 𝑡2 𝑡2 𝑡2 得𝑦=±√ 1− ，不妨设𝑃(𝑡,√ 1− )，𝑄(𝑡,−√ 1− )， 则△𝑂𝑃𝑄的面积𝑆 = 2 2 2 1 ×|𝑡|×2√ 1− 𝑡2 = √ 2 ， 解得𝑡2 =1，所以𝑥2+𝑥2 =2，𝑦2+𝑦2 =1. 当直线𝑙的斜率 2 2 2 1 2 1 2 𝑦 =𝑘𝑥+𝑚, 存在时，设直线𝑙的方程为𝑦 =𝑘𝑥+𝑚， 由{ 𝑥2 +𝑦2 =1, 得(1+2𝑘2)𝑥2+4𝑘𝑚𝑥+2(𝑚2− 2 1)=0，则𝛥 =8(2𝑘2−𝑚2+1)>0， 所以𝑥 +𝑥 =− 4𝑘𝑚 ，𝑥 𝑥 = 2(𝑚2−1) ， 所以 1 2 1+2𝑘2 1 2 1+2𝑘2 |𝑃𝑄 ∣=√ 1+𝑘2⋅√ (𝑥 +𝑥 )2−4𝑥 𝑥 = 2√ 2⋅√ 1+𝑘2⋅√ 2𝑘2−𝑚2+1 ， 又坐标原点𝑂到直线𝑃𝑄 1 2 1 2 1+2𝑘2 的距离𝑑 = |𝑚| ， 所以△𝑂𝑃𝑄的面积𝑆 = 1 ×|𝑃𝑄|×𝑑 = 1 × 2√ 2⋅√ 1+𝑘2⋅√ 2𝑘2−𝑚2+1 × √ 1+𝑘2 2 2 1+2𝑘2 |𝑚| = √ 2 ，化简得2𝑚2 =2𝑘2+1，所以𝑥2+𝑥2 =(𝑥 +𝑥 )2−2𝑥 𝑥 = 16𝑘2𝑚2 − √ 1+𝑘2 2 1 2 1 2 1 2 (1+2𝑘2)2 4(𝑚2−1) = 4𝑘2+2 =2，𝑦2+𝑦2 =1− 𝑥 1 2 +1− 𝑥 2 2 =1.综上可知，𝑥2+𝑥2 =2，𝑦2+𝑦2 =1， 1+2𝑘2 1+2𝑘2 1 2 2 2 1 2 1 2 均为定值．