江苏省南京市六校联合体2024-2025学年高二上学期10月月考数学试题参考答案及评分标准_2024-2025高二（7-7月题库）_2024年10月试卷

2024-2025 学年第一学期 10 月六校联合调研参考答案及评分标准 高二数学 一、单项选择题 1、B 2、A 3、C 4、B 5、C 6、C 7、D 8、C 二、多项选择题 9、ABD 10、AC 11、BCD 三、填空题 2 4 5 12、 13、 14、4 5 5 四、解答题 15解：(1)因为bsin2A＝asinB，所以2bsinAcosA＝asinB． 根据正弦定理，得2sinBsinAcosA＝sinAsinB， ……………… 2分 因为sinB≠0，sinA≠0，所以cosA＝1 ． ………………… 4分 2 又A∈(0，π)，所以A＝π． ………………… 6分 3 1 1 3 3 3 （2）在VABC中，由已知S  bcsinA bc  ,bc6， ············8分 ABC 2 2 2 2 π 因为A ，a 7 3 1 由余弦定理可得a2 b2 c2 2bccosA，即7bc22bc2bc ，··············10分 2 即7bc2 3bc，又b0,c0所以bc5. 所以VABC的周长周长为5 7.····································································13分 16解： （1）证明：因为PA是一条母线，所以PA平面ABC， 而BC平面ABC，则PABC，··································································· 2分 因为AB是底面一条直径，C是AB 的中点，所以ACB90，即AC BC，··········4分 又PA,AC平面PAC且PAAC A， 所以BC 平面PAC，而BC平面PBC，则平面PAC 平面PBC.·······················6分 试卷第1页，共5页 {#{QQABLQQEoggoABAAAAhCAQ1yCAOQkhGAAagOhBAEsAAASANABAA=}#}（2）设PA2AB4，则PB2 5， 因为C是AB 的中点，O为底面圆心，所以CO平面PAB， 作OE PB，交PB于点E连接CE， 由OEPB，CE PB可知，CEO是二面角APBC的平面角.·······················10分 4 2 5 3 5 则PBOEPABO，即OE   ，在直角COE中，CE  OC2OE2  . 2 5 5 5 2 5 5 2 所以 cosCEO  . 3 5 3 5 2 故二面角APBC的余弦值为 .··································································15分 3  1 pq   3 17解：（1）由题意得 ，·······························································4分 1  (1 p)q   6 2 1 解得 p ,q .··························································································6分 3 2 (2)比赛结束后，甲、乙个人得分可能为0，2，3，5. 记甲得分为i分的事件为C i0,2,3,5，乙得分为i分的事件为D i0,2,3,5， i i C,D 相互独立， i i 记两轮投篮后甲总得分不低于8分为事件E， 则EC D C D C D ，且C D ，C D ，C D 彼此互斥. 3 5 5 3 5 5 3 5 5 3 5 5 1 易得P（C ）= ，························································································8分 3 6 3 2 1 1 3 2 1 P（D ）=(1 )  ，P（C ）= ，P（D ）=   ， 3 5 5 4 3 6 3 4 3 2 所以P(E) P(C D C D C D ) P(C D )P(C D )P(C D ) 3 5 5 3 5 5 3 5 5 3 5 5 1 1 1 1 1 1 11 =       . 6 2 3 6 3 2 36 11 所以两轮投篮后，甲总得分不低于8分的概率为 .·········································15分 36 试卷第2页，共5页 {#{QQABLQQEoggoABAAAAhCAQ1yCAOQkhGAAagOhBAEsAAASANABAA=}#}18解：（1）法1：（待定系数法） 设圆M的方程为 xa 2  yb 2 r2， 因为圆M过点A(3,3)，所以 3a 2  3b 2 r2①，······································2分 又因为圆心M在直线2x y50上，所以2ab50②，·······························4分 a2b5 直线x2y50与圆M相切，得到r  ③，·······································6分 5 由①②③解得：a2，b1，r  5因此圆M的方程为(x2)2(y1)2 5.······· 7分 法2：（几何性质） 因为直线2x y50与直线x2y50垂直， 2x y50 x 1 又因为圆心M在直线2x y50上，联立方程 ，解得 ·········4分 x2y50 y 3 设两直线的交点为B(1,3)，由圆的几何性质，点B(1,3)在圆上，且为直线与圆的切点， 又因为圆M过点A(3,3)，且所以圆心M在直线x2上，又圆心M也在直线2x y50上， x2 x 2 联立方程 ，解得 ，故圆心M(2,1)，····································6分 2x y50 y 1 所以半径r  AM  5，因此圆M的方程为(x2)2 (y1)2 5.······················7分 （2）设A(x,y)，因为A为线段BD的中点，所以B(2x,2y2)，  24 x (x2)2 (y1)2 5 x0   13 因为A，B在圆M上，所以 ，解得 或 ········12分  (2x2)2 (2y1)2 5 y 0  y- 16   13 当A(0,0)时，直线l的方程为x0；···························································· 14分 24 16 5 当A( ,- )时，故直线l的方程为y x2，即5x12y240.··················16分 13 13 12 综上，直线l的方程为x0或5x12y240.···············································17分 试卷第3页，共5页 {#{QQABLQQEoggoABAAAAhCAQ1yCAOQkhGAAagOhBAEsAAASANABAA=}#}x2 y2 1 c 1 19解：（1）由于椭圆C:  1(ab0)的离心率为 ，故  ， a2 b2 2 a 2 又 AF ac6，所以a4，c2，b2 a2c2 12， 1 2 x2 y2 所以椭圆C的方程为  1.······································································4分 16 12 （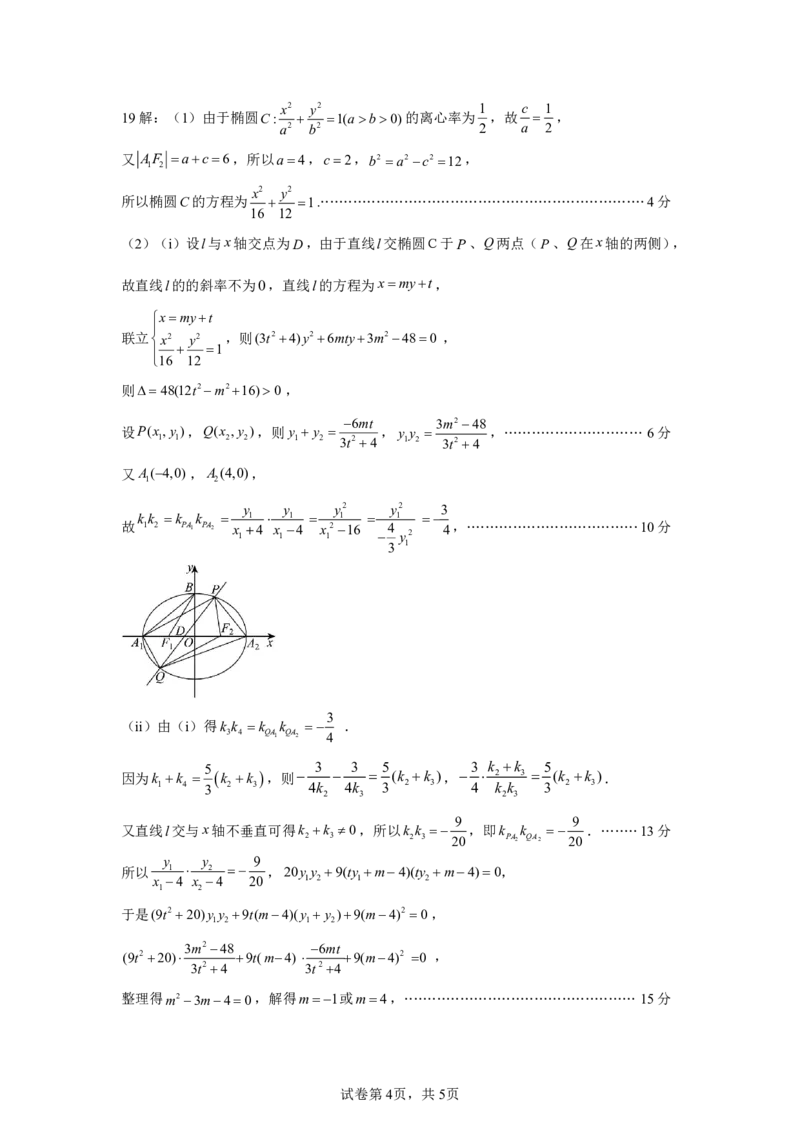2）（i）设l与x轴交点为D，由于直线l交椭圆Ｃ于P、Q两点（P、Q在x轴的两侧）， 故直线l的的斜率不为0，直线l的方程为xmyt， xmyt  联立x2 y2 ，则(3t24)y26mty3m2480 ，   1 16 12 则48(12t2m216)0 ， 6mt 3m248 设P(x,y )，Q(x ,y )，则y  y  ，y y  ，······························ 6分 1 1 2 2 1 2 3t24 1 2 3t24 又A(4,0)，A (4,0)， 1 2 y y y2 y2 3 kk k k  1  1  1  1  故 1 2 PA1 PA2 x 4 x 4 x2 16 4 4 ，·····································10分 1 1 1  y2 3 1 3 （ii）由（i）得k k k k  ． 3 4 QA1 QA2 4 5 3 3 5 3 k k 5 因为k k  k k ，则   (k k )，  2 3  (k k )． 1 4 3 2 3 4k 4k 3 2 3 4 k k 3 2 3 2 3 2 3 9 9 又直线l交与x轴不垂直可得k k 0，所以k k  ，即k k  ．········13分 2 3 2 3 20 PA2 QA2 20 y y 9 所以 1  2  ，20y y 9(ty m4)(ty m4)0， x 4 x 4 20 1 2 1 2 1 2 于是(9t220)y y 9t(m4)(y  y )9(m4)2 0， 1 2 1 2 3m248 6mt (9t220) 9t(m4)  9(m4)2 0 ， 3t24 3t24 整理得m23m40，解得m1或m4，··················································15分 试卷第4页，共5页 {#{QQABLQQEoggoABAAAAhCAQ1yCAOQkhGAAagOhBAEsAAASANABAA=}#}3m248 因为P、Q在x轴的两侧，所以y y  0，4m4，························ 16分 1 2 3t24 又m1时，直线l与椭圆C有两个不同交点， 因此m1，直线l恒过点D(1,0).································································ 17分 试卷第5页，共5页 {#{QQABLQQEoggoABAAAAhCAQ1yCAOQkhGAAagOhBAEsAAASANABAA=}#}