江苏省南京市六校联合体2024-2025学年高二上学期10月月考数学试题_2024-2025高二（7-7月题库）_2024年10月试卷_1025江苏省南京市六校联合体2024-2025学年高二上学期10月月考

2024-2025 学年第一学期 10 月六校联合调研试题 高二数学 本试卷共 4页，19题．全卷满分150分．考试用时 120分钟． 一、单项选择题：本题共8小题，每小题 5 分，共40 分．每小题给出的四个选 项中，只有一项符合题目要求. 1．已知复数z满足(12i)z 34i，则|z| ( ) A． 3 B． 5 C．3 D．5 2．设a为实数，已知直线l ：ax3y20，l ：6xa3y40，若l //l ，则a ( ) 1 2 1 2 A.6 B.-3 C.6或-3 D.-6或3 x2 y2 3．已知焦点在x轴上的椭圆  1的焦距为6，则实数m等于 ( ) m 3 3 21 A. B. C.12 D. 126 3 4 4 cos  2  π 4．已知  ，则tan  ( ) sin( )  4 4 A． 3 B．3 C． 3 D．3 5. 设直线xay20与圆C:x2 y22 16相交于A，B两点，且ABC的面积为8，则 a ( ) A.  2 B. 1 C.1 D. 2  6．已知M 为直线l:2x3y10上的动点，点P满足MP2,4，则点P的轨迹方程为 ( ) 49 A．3x2y90 B．(x2)2(y4)2  13 49 C．2x3y90 D．(x2)2(y4)2  13 7．如图，两个相同的正四棱台密闭容器内装有纯净水，AB8,AB 2，图1中水面高度 1 1 1 2 恰好为棱台高度的 ，图2中水面高度为棱台高度的 ，若图1和图2中纯净水的体积分别 2 3 V 为V,V ，则 1 ( ) 1 2 V 2 试卷第1页，共4页 {#{QQABLQQEoggoABAAAAhCAQ1yCAOQkhGAAagOhBAEsAAASANABAA=}#}2 6 287 387 A． B． C． D． 3 5 208 208 8．关于椭圆有如下结论：“过椭圆 x2  y2 1ab0上一点Px ,y 作该椭圆的切线， a2 b2 0 0 x x y y x2 y2 切线方程为 0  0 1.”设椭圆C：  1ab0的左焦点为F，右顶点为A，过 a2 b2 a2 b2 F且垂直于x轴的直线与C的一个交点为M，过M作椭圆的切线l，若切线l的斜率k 与直 1 线AM 的斜率k 满足k 2k 0，则椭圆C的离心率为 ( ) 2 1 2 1 3 2 2 A． B． C． D． 3 3 3 2 二、多项选择题：本题共 3小题，每小题 6分，共18分．在每小题给出的选项 中，有多项符合题目要求．全部选对的得 6分，部分选对的得部分分，有选错 的得0分. 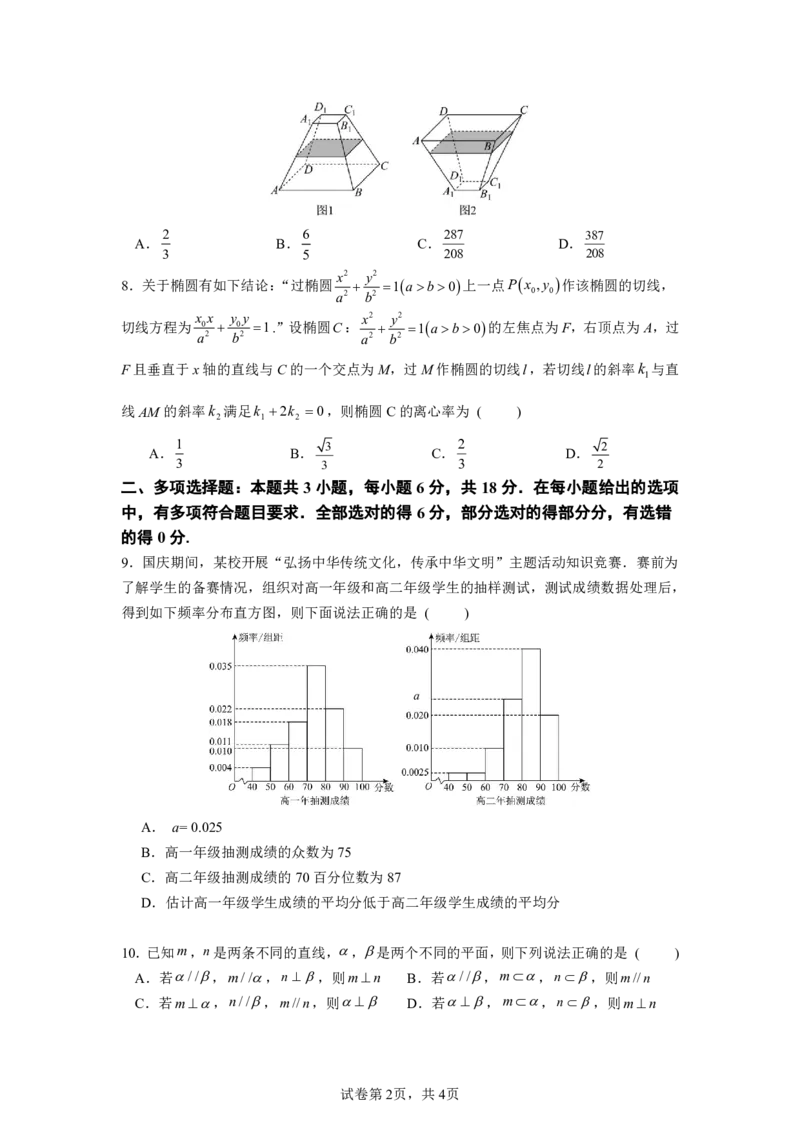9．国庆期间，某校开展“弘扬中华传统文化，传承中华文明”主题活动知识竞赛．赛前为 了解学生的备赛情况，组织对高一年级和高二年级学生的抽样测试，测试成绩数据处理后， 得到如下频率分布直方图，则下面说法正确的是 ( ) a A． a=0.025 B．高一年级抽测成绩的众数为75 C．高二年级抽测成绩的70百分位数为87 D．估计高一年级学生成绩的平均分低于高二年级学生成绩的平均分 10．已知m，n是两条不同的直线，，是两个不同的平面，则下列说法正确的是 ( ) A．若//，m//，n，则mn B．若//，m，n，则m//n C．若m，n//，m//n，则 D．若，m，n，则mn 试卷第2页，共4页 {#{QQABLQQEoggoABAAAAhCAQ1yCAOQkhGAAagOhBAEsAAASANABAA=}#}11．已知圆C：(x2)2  y2 4 ，以下四个命题表述正确的是 ( ) A．若圆x2 y210x8ym0与圆C恰有3条公切线，则m=16 B．圆x2y22y0与圆C的公共弦所在直线为2x y0 C．直线(2m1)x(3m2)y5m30与圆C恒有两个公共点 D．点P为y轴上一个动点，过点P作圆C的两条切线，切点分别为A，B，且A，B的 中点为M，若定点N（5，3），则MN的最大值为6 三、填空题：本题共 3 小题，每小题 5 分，共 15 分.请把答案直接填写在答题 卡相应位置上. 12．从分别写有1,2,3,4,5的五张卡片中任取两张，则抽到的两张卡片上的数字之和是3的倍 数的概率为 . x2 y2 13. 已知P为椭圆C： + 1上的点，A(1，0)， 则线段PA长度的最小值为 . 9 4 14．已知A0,2，B1,0，Ct,0，点D是直线AC上的动点，若AD≤ 3BD恒成立，则 正整数t 的最小值是 . 四、解答题：本题共5小题，共77分．解答应写出文字说明、证明过程或演算 步骤． 15．（本小题满分13分） 记ABC的内角A，B，C的对边分别为a，b，c，且bsin2A＝asinB． (1)求角A； 3 3 (2)若a 7，ABC的面积为 ，求VABC的周长. 2 16．（本小题满分15分） 如图，圆柱OO 1 中，PA是一条母线，AB是底面一条直径，C是AB 的中点. (1)证明：平面PAC 平面PBC ； (2)若PA2AB4，求二面角APBC的余弦值. 试卷第3页，共4页 {#{QQABLQQEoggoABAAAAhCAQ1yCAOQkhGAAagOhBAEsAAASANABAA=}#}17．（本小题满分15分） 某校为了厚植文化自信、增强学生的爱国情怀，特举办“中国诗词精髓”知识竞赛活动， 比赛中只有A，B两道题目，比赛按先A题后B题的答题顺序各答1次，答对A题得2分， 答对B题得3分，答错得0分.已知学生甲答对A题的概率为p，答对B题的概率为q，其 3 2 中0 p1，0q1，学生乙答对A题的概率为 ，答对B题的概率为 ，且甲乙各自在 4 3 1 1 答A，B两题的结果互不影响.已知甲比赛后得5分的概率为 ，得3分的概率为 . 3 6 （1）求p，q的值； （2）求比赛后，甲乙总得分不低于8分的概率. 18．（本小题满分17分） 已知圆M过点A(3,3)，圆心M在直线2x y50上，且直线x2y50与圆M相切. （1）求圆M的方程； （2）过点D(0,2)的直线l交圆M于A，B两点.若A为线段DB的中点，求直线l的方程. 19．（本小题满分17分） x2 y2 1 已知椭圆C:  1(ab0)的离心率为 ，A、A 分别为椭圆C的左、右顶点，F 、 a2 b2 2 1 2 1 F 分别为椭圆C的左、右焦点， AF 6． 2 1 2 (1)求椭圆C的方程； (2)设与x轴不垂直的直线l交椭圆C于P、Q两点（P、Q在x轴的两侧），记直线AP，AP， 1 2 AQ，AQ的斜率分别为k ，k ，k ，k ． 2 1 1 2 3 4 （i）求kk 的值； 1 2 5 （ii）若k k  k k ，问直线PQ是否过定点，若过定点，求出定点；若不过定点， 1 4 3 2 3 说明理由. 试卷第4页，共4页 {#{QQABLQQEoggoABAAAAhCAQ1yCAOQkhGAAagOhBAEsAAASANABAA=}#}