文档内容
2024-2025 学年江苏省南京市第一中学高二下学期 3 月月考数学试卷
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
⃗ ⃗ ⃗ ⃗ ⃗ ⃗ ⃗
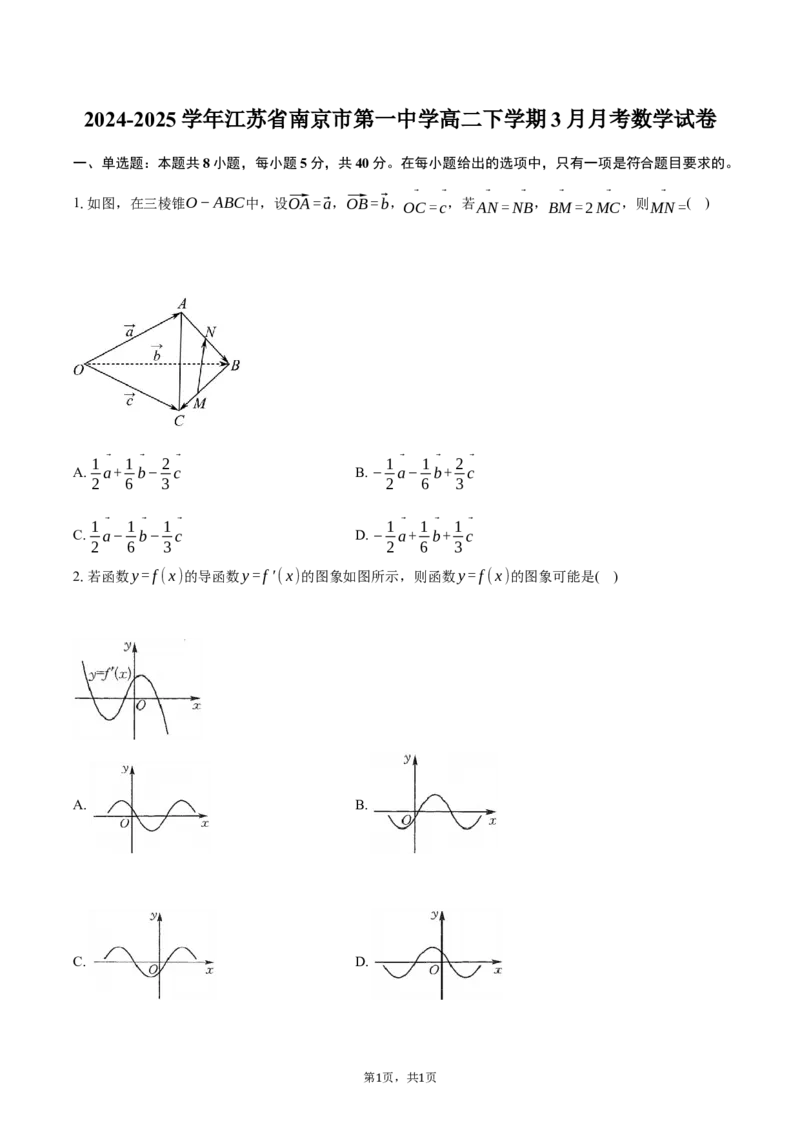
1.如图,在三棱锥O−ABC中,设⃗OA=⃗a,⃗OB=⃗b, OC=c ,若 AN=NB , BM=2MC ,则 MN=( )
1⃗ 1⃗ 2⃗ 1⃗ 1⃗ 2⃗
A. a+ b− c B. − a− b+ c
2 6 3 2 6 3
1⃗ 1⃗ 1⃗ 1⃗ 1⃗ 1⃗
C. a− b− c D. − a+ b+ c
2 6 3 2 6 3
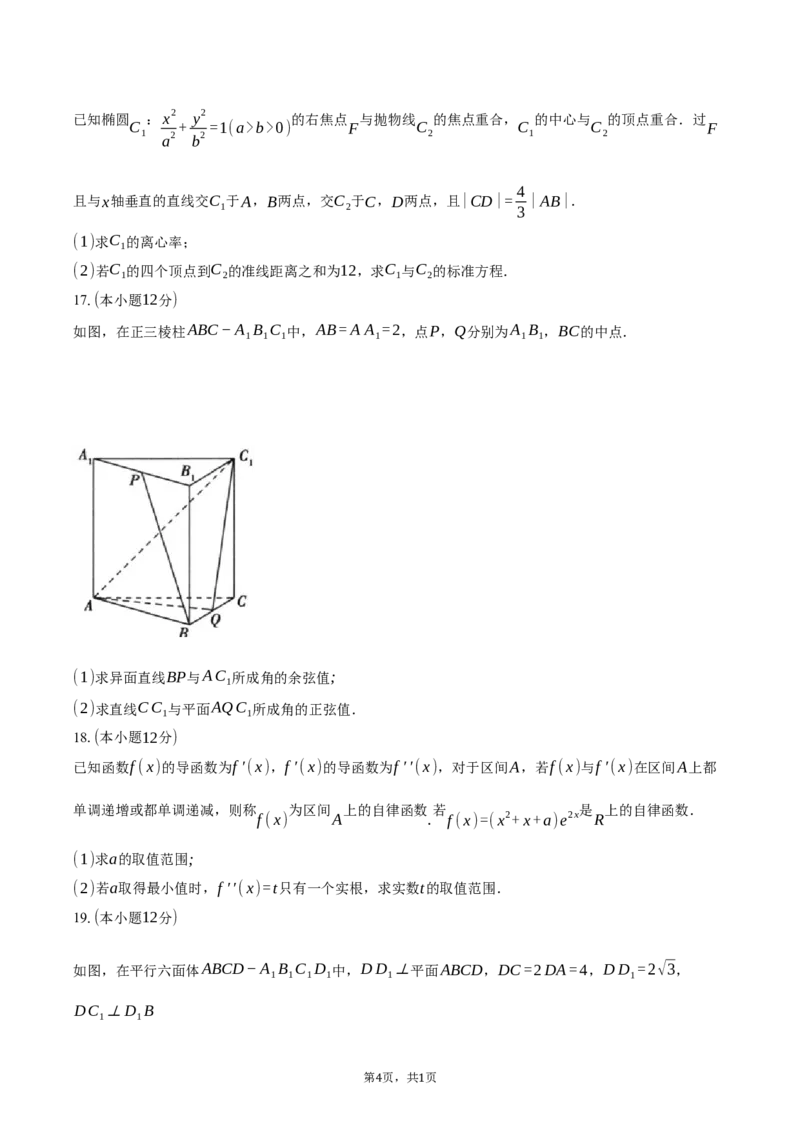
2.若函数y=f(x)的导函数y=f ′(x)的图象如图所示,则函数y=f(x)的图象可能是( )
A. B.
C. D.
第 页,共 页
1 13.三名学生分别从4门选修课中选修一门课程,不同的选法有( )
A. 24种 B. 81种 C. 64种 D. 32种
4.若⃗ ,⃗ ,则 ⃗ ⃗ ⃗ ⃗ ( )
a=(−1,2,1) b=(1,2,−3) (a+b)⋅(2a−b)=
A. −2 B. 4 C. −21 D. 26
1 1 1
5.已知等比数列{a }满足 + + =2,a =2,记S 为其前n项和,则S =( )
n a a a 2 n 3
1 2 3
A. 1 B. 2 C. 4 D. 8
6.已知圆O:x2+ y2=1,直线x−y+a=0上存在点P,过点P作圆O的两条切线,切点为A,B,使得
∠APB=60∘,则a的取值范围( )
A. [−2,2] B. [−∞,2] C. [−2√2,2√2] D. [−2√2,+∞]
7.若函数
f(x)=
x3
−
a
x2+x+1
在区间(1
,3
)上有极值点,则实数
a
的取值范围是( )
3 2 2
A. ( 5) B. [ 5) C. ( 10) D. [ 10)
2, 2, 2, 2,
2 2 3 3
8.用黑白两种颜色随机地染如图所示表格中6个格子,每个格子染一种颜色,并且从左到右数,不管数到
哪个格子,总有黑色格子不少于白色格子的染色方法种数为( )
A. 15 B. 16 C. 18 D. 20
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.给出下列命题,其中正确的是( )
A. 若 ⃗ ⃗ ⃗ 是空间的一个基底,则 ⃗ ⃗ ⃗ ⃗ 也是空间的一个基底
{a,b,c} {a,b,b+c}
B. 在空间直角坐标系中,点P(−2,4,3)关于坐标平面yOz的对称点是(−2,−4,−3)
⃗ 1 ⃗ 3 ⃗
C. 若空间四个点P,A,B,C满足PC= PA+ PB,则A,B,C三点共线
4 4
D. 平面 α 的一个法向量为 m ⃗ =(1,3,−4) ,平面 β 的一个法向量为⃗ n=(−2,−6,k). 若 α//β ,则 k=8
10.某种产品的加工需要经过5道工序,则以下说法正确的是( )
第 页,共 页
2 1A. 如果其中某道工序不能放在最后,那么有96种加工顺序
B. 如果其中某2道工序不能放在最前,也不能放在最后,那么有36种加工顺序
C. 如果其中某2道工序必须相邻,那么有24种加工顺序
D. 如果其中某2道工序不能相邻,那么有72种加工顺序
11.在长方体ABCD−A B C D 中,AB=AD=1,A A =2,E为A D 的中点,动点P在长方体
1 1 1 1 1 1 1
ABCD−A 1 B 1 C 1 D 1 内(含表面),且满足 A ⃗ P=λA ⃗ C+μA ⃗ E ,记动点P的轨迹为Ω,则( )
3√33
A. Ω的面积为
8
B. 平面A BC 与Ω所在平面平行
1 1
1
C. 当λ= 时,存在点P,使得A P⊥BD
2 1 1
D. 当μ=1时,三棱锥P−ABC的体积为定值
三、填空题:本题共3小题,每小题5分,共15分。
12.在空间直角坐标系中,A(1,1,1)、B(2,3,4),平面BCD的一个法向量是(−1,2,1),则点A到平面
BCD的距离为 .
13.圆x2+ y2−4=0与圆x2+ y2−4x+4 y−12=0的公共弦长为 .
14.已知数列 的首项 ,其前 项和为 ,且满足 若对任意的 ,
{a } a =a n S S +S =3n2(n≥2). n∈N∗
n 1 n n n−1
a b>0) F C C C F
1 a2 b2 2 1 2
4
且与x轴垂直的直线交C 于A,B两点,交C 于C,D两点,且|CD|= |AB|.
1 2 3
(1)求C 的离心率;
1
(2)若C 的四个顶点到C 的准线距离之和为12,求C 与C 的标准方程.
1 2 1 2
17.(本小题12分)
如图,在正三棱柱ABC−A B C 中,AB=A A =2,点P,Q分别为A B ,BC的中点.
1 1 1 1 1 1
(1)求异面直线BP与AC 所成角的余弦值;
1
(2)求直线CC 与平面AQC 所成角的正弦值.
1 1
18.(本小题12分)
已知函数f(x)的导函数为f ′(x),f ′(x)的导函数为f ′′(x),对于区间A,若f(x)与f ′(x)在区间A上都
单调递增或都单调递减,则称 为区间 上的自律函数 若 是 上的自律函数.
f(x) A . f(x)=(x2+x+a)e2x R
(1)求a的取值范围;
(2)若a取得最小值时,f ′′(x)=t只有一个实根,求实数t的取值范围.
19.(本小题12分)
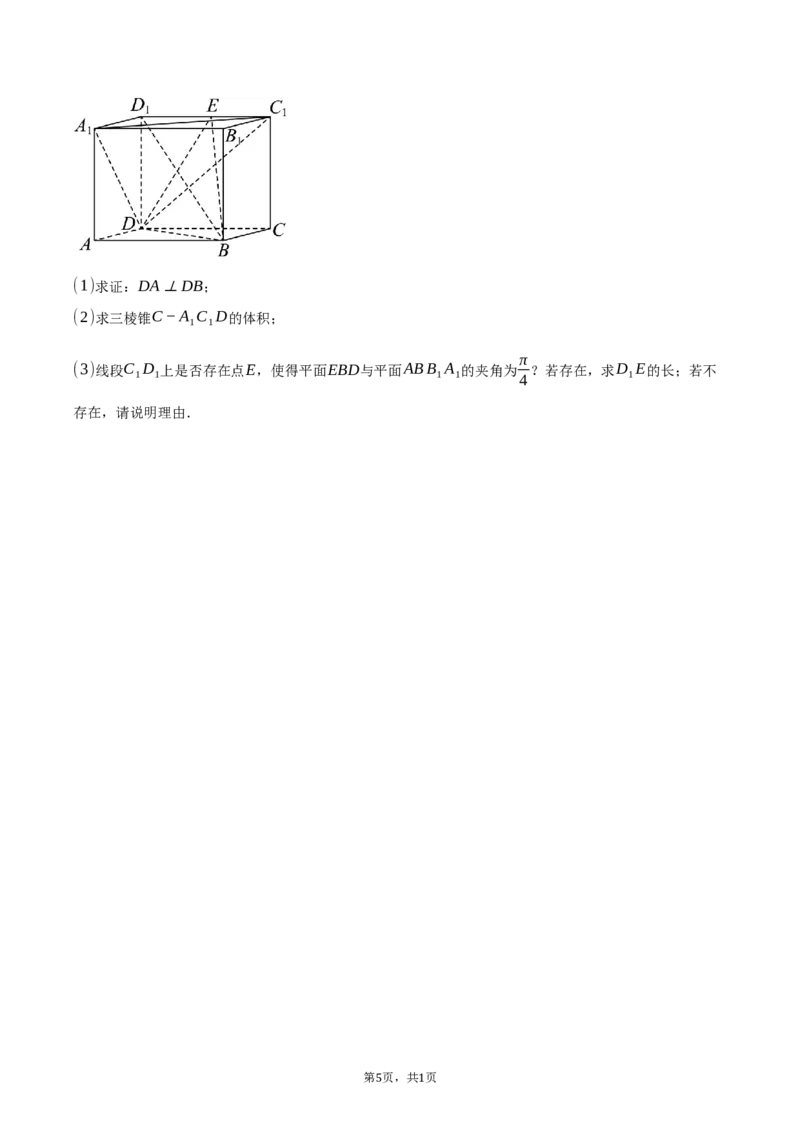
如图,在平行六面体ABCD−A B C D 中,DD ⊥平面ABCD,DC=2DA=4,DD =2√3,
1 1 1 1 1 1
DC ⊥D B
1 1
第 页,共 页
4 1(1)求证:DA⊥DB;
(2)求三棱锥C−A C D的体积;
1 1
π
(3)线段C D 上是否存在点E,使得平面EBD与平面ABB A 的夹角为 ?若存在,求D E的长;若不
1 1 1 1 4 1
存在,请说明理由.
第 页,共 页
5 1参考答案
1.A
2.C
3.C
4.A
5.D
6.C
7.C
8.D
9.ACD
10.ABD
11.ACD
12.√6
13.2√2
14.(9 15)
,
4 4
15.解:(1)无重复数字的四位密码相当于从6个数字中任取4个的排列,
所以无重复数字的密码箱的四位密码个数为 .
A4=6×5×4×3=360
6
最高位上的数字为 的无重复数字的四位偶数,其个位是 之一,共有 个;
(2) 2 0,4 C1A2
2 4
最高位上的数字为 之一的无重复数字的四位偶数,其个位是 之一,共有 个,
3,5 0,2,4 C1C1A2
2 3 4
最高位上的数字为 的无重复数字的四位偶数,其个位是 之一,共有 个,
4 0,2 C1A2
2 4
所以比 大的无重复数字的四位偶数个数为 .
2000 2C1A2+C1C1A2=120
2 4 2 3 4
16.解:(1)由题意设抛物线C 的方程为:y2=4cx,焦点坐标F为(c,0),
2
因为AB⊥x轴,将x=c代入抛物线的方程可得y2=4c2,所以|y|=2c,
所以弦长|CD|=4c,
第 页,共 页
6 1将 代入椭圆 的方程可得 c2 b4 ,所以 b2,
x=c C y2=b2 (1− )= |y|=
1 a2 a2 a
所以弦长 2b2,
|AB|=
a
4 4 2b2
再由|CD|= |AB|,可得4c= ⋅ ,即3ac=2b2=2(a2−c2 ),
3 3 a
1
整理可得2c2+3ac−2a2=0,即2e2+3e−2=0,e∈(0,1),所以解得e= ,
2
1
所以C 的离心率为 ;
1 2
(2)由椭圆的方程可得4个顶点的坐标分别为:(±a,0),(0,±b),
而抛物线的准线方程为:x=−c,
c 1
所以由题意可得2c+a+c+a−c=12,即a+c=6,而由(1)可得 = ,所以解得:a=4,c=2,所以
a 2
b2=a2−c2=16−4=12,
x2 y2
所以C 的标准方程为: + =1,C 的标准方程为:y2=8x.
1 16 12 2
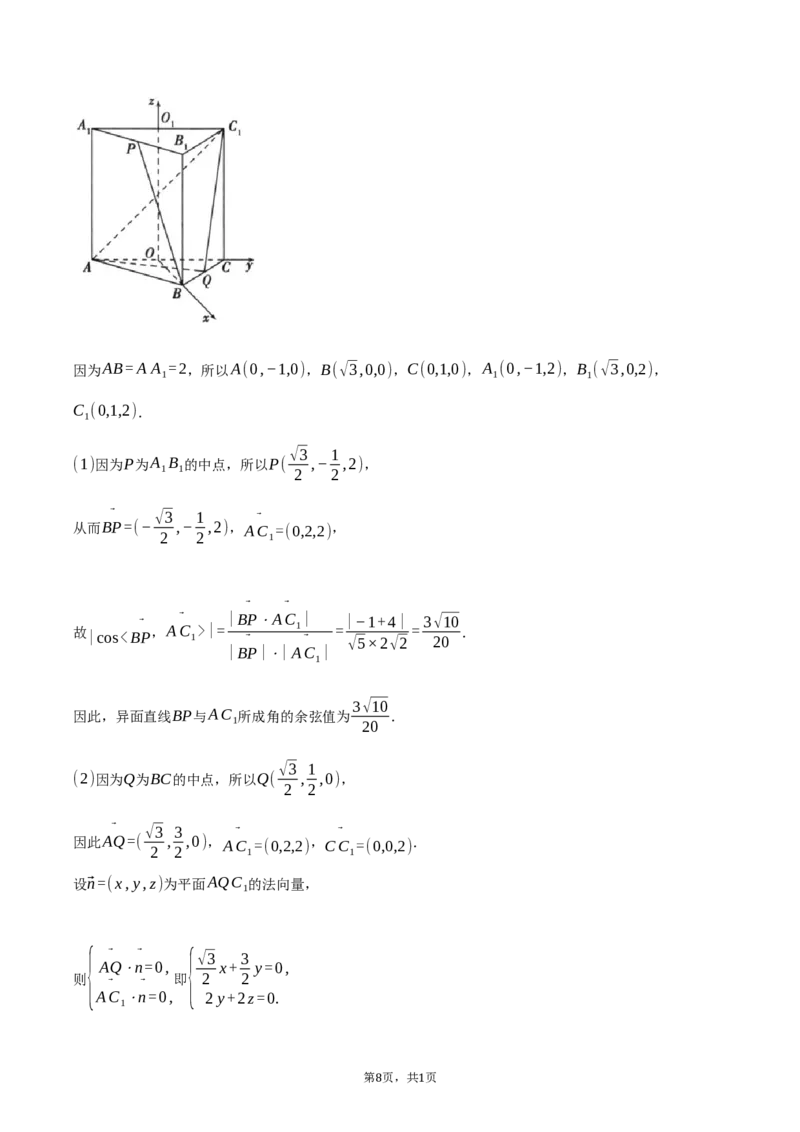
17.解:如图,在正三棱柱ABC−A B C 中,设AC,A C 的中点分别为O,O ,连接OB,OO ,
1 1 1 1 1 1 1
⃗ ⃗ ⃗
则OB⊥OC,OO
1
⊥OC,OO
1
⊥OB,以
{OB,OC,OO }
为基底,建立空间直角坐标系O−xyz.
1
第 页,共 页
7 1因为AB=A A =2,所以A(0,−1,0),B(√3,0,0),C(0,1,0),A (0,−1,2),B (√3,0,2),
1 1 1
C (0,1,2).
1
√3 1
(1)因为P为A B 的中点,所以P( ,− ,2),
1 1 2 2
⃗ √3 1 ⃗
从而BP=(− ,− ,2),AC =(0,2,2) ,
2 2 1
⃗ ⃗
⃗ |BP⋅AC | |−1+4| 3√10
故|cos|=
⃗
1
⃗
=
√5×2√2
=
20
.
|BP|⋅|AC |
1
3√10
因此,异面直线BP与AC 所成角的余弦值为 .
1 20
√3 1
(2)因为Q为BC的中点,所以Q( , ,0),
2 2
⃗ √3 3 ⃗ ⃗
因此AQ=( , ,0),AC =(0,2,2) ,CC =(0,0,2) .
2 2 1 1
设⃗n=(x,y,z)为平面AQC 的法向量,
1
{ ⃗ ⃗ {√3 3
AQ⋅n=0, x+ y=0,
则 即 2 2
⃗ ⃗
AC ⋅n=0, 2y+2z=0.
1
第 页,共 页
8 1⃗
不妨取n=(√3,−1,1) .
设直线CC 与平面AQC 所成角为θ,
1 1
⃗ ⃗
则sinθ=|cos|= |CC 1 ⋅n| = 2 = √5 ,
1 ⃗ ⃗ 2×√5 5
|CC |·|n|
1
√5
所以直线CC 与平面AQC 所成角的正弦值为 .
1 1 5
18.解: 由 ,
(1) f(x)=(x2+x+a)e2x
得 ,
f ′(x)=(2x+1)e2x+2(x2+x+a)e2x=(2x2+4x+2a+1)e2x
,
f ′′(x)=(4x+4)e2x+2(2x2+4x+2a+1)e2x=(4x2+12x+4a+6)e2x
因为 是 上的自律函数,且 在 上不可能恒小于零,
f(x)=(x2+x+a)e2x R f ′′(x) R
所以f(x)与f ′(x)在区间R上都单调递增,
所以{4x2+12x+4a+6≥0在
上恒成立,
R
2x2+4x+2a+1≥0
所以{144−16(4a+6)≤0,解得 3,
a≥
16−8(2a+1)≤0 4
所以 的取值范围为[3 );
a ,+∞
4
3
(2)当a= 时,f ′′(x)=(4x2+12x+9)e2x=(2x+3) 2e2x,
4
令 ,
ℎ(x)=f ′′(x)=(4x2+12x+9)e2x
则 ,
ℎ′(x)=(8x+12)e2x+2(4x2+12x+9)e2x=(8x2+32x+30)e2x
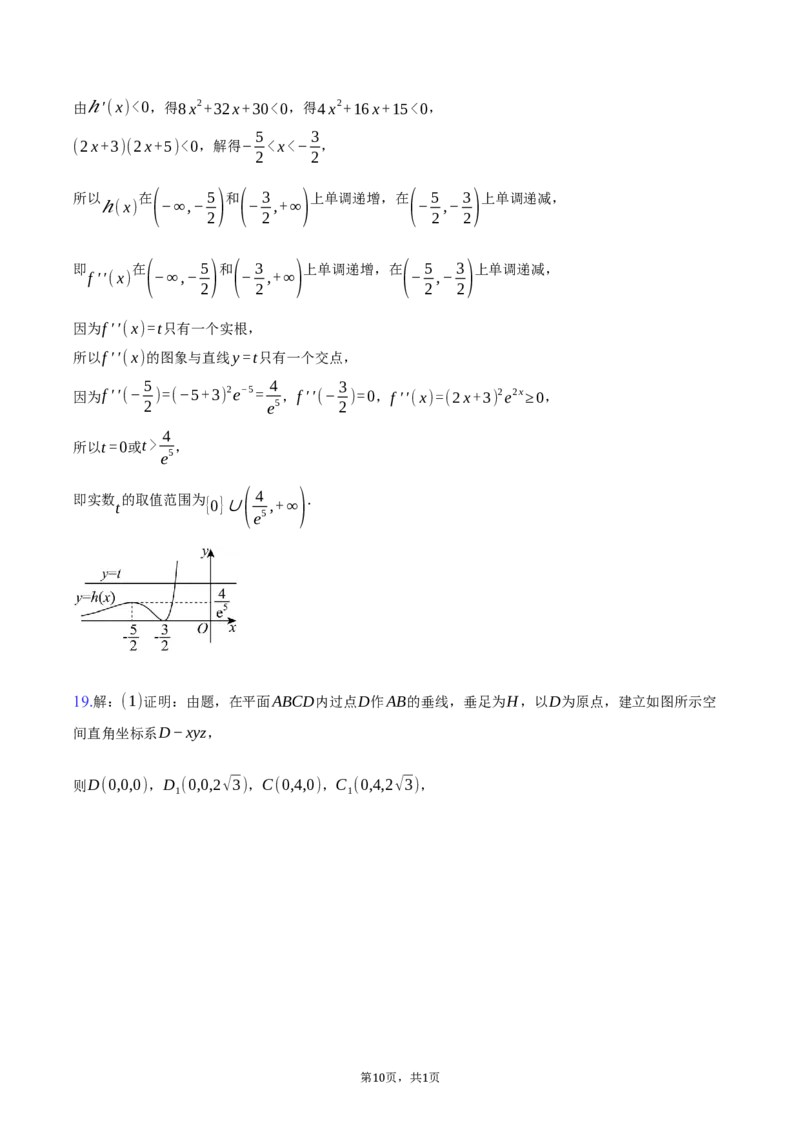
由ℎ′(x)>0,得8x2+32x+30>0,得4x2+16x+15>0,
5 3
(2x+3)(2x+5)>0,解得x<− 或x>− ,
2 2
第 页,共 页
9 1由ℎ′(x)<0,得8x2+32x+30<0,得4x2+16x+15<0,
5 3
(2x+3)(2x+5)<0,解得− ,
e5
即实数 的取值范围为 ( 4 ).
t {0}∪ ,+∞
e5
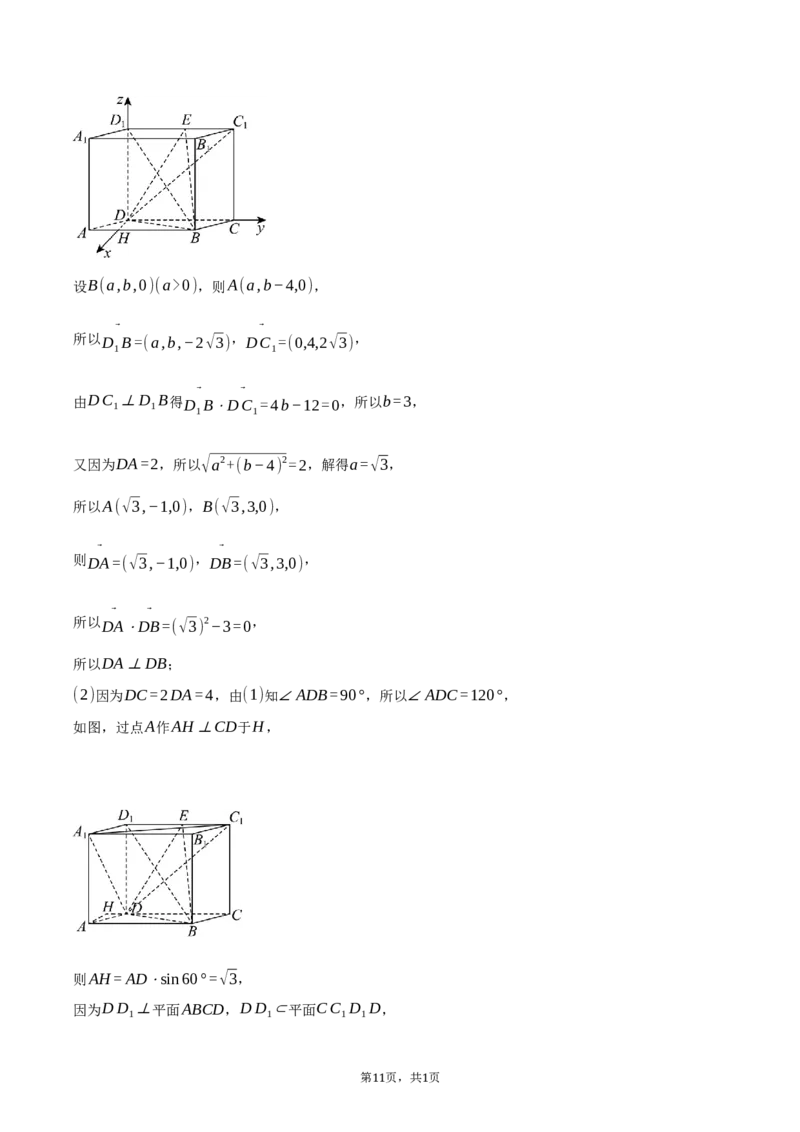
19.解:(1)证明:由题,在平面ABCD内过点D作AB的垂线,垂足为H,以D为原点,建立如图所示空
间直角坐标系D−xyz,
则D(0,0,0),D (0,0,2√3),C(0,4,0),C (0,4,2√3),
1 1
第 页,共 页
10 1设B(a,b,0)(a>0),则A(a,b−4,0),
⃗ ⃗
所以D B=(a,b,−2√3) ,DC =(0,4,2√3) ,
1 1
⃗ ⃗
由DC
1
⊥D
1
B得D
B⋅DC
=4b−12=0,所以b=3,
1 1
又因为DA=2,所以√a2+(b−4) 2=2,解得a=√3,
所以A(√3,−1,0),B(√3,3,0),
⃗ ⃗
则DA=(√3,−1,0) ,DB=(√3,3,0) ,
⃗ ⃗
所以DA⋅DB=(√3) 2−3=0,
所以DA⊥DB;
(2)因为DC=2DA=4,由(1)知∠ADB=90°,所以∠ADC=120°,
如图,过点A作AH⊥CD于H,
则AH=AD⋅sin60°=√3,
因为DD ⊥平面ABCD,DD ⊂平面CC D D,
1 1 1 1
第 页,共 页
11 1所以平面CC D D⊥平面ABCD,平面CC D D∩平面ABCD=DC,AH⊂平面ABCD,
1 1 1 1
所以AH⊥平面CC D D,
1 1
1 1 1
所以V =V = S ⋅AH= ⋅( ×DC×CC )⋅AH
C−A 1 C 1 D A 1 −CC 1 D 3 △CC 1 D 3 2 1
1 1
= × ×4×2√3×√3=4;
3 2
(3)由(1)得平面ABB A 的一个法向量为⃗n =(1,0,0),
1 1 1
⃗ ⃗
假设存在E点满足条件,设D E=λD C ,(0≤λ≤1),
1 1 1
⃗ ⃗ ⃗
则DE=DD +D E=(0,4λ,2√3) ,
1 1
设平面EBD的一个法向量为⃗n =(x ,y ,z ),
2 2 2 2
{⃗ ⃗
n ⋅DE=0 {4λ y +2√3z =0
2 2 2
由 ,得 ,
⃗ ⃗ √3x +3 y =0
n ⋅DB=0 2 2
2
令y
2
=√3,则x
2
=−3,z
2
=−2λ,所以n ⃗ =(−3,√3,−2λ) ,
2
⃗ ⃗
⃗ ⃗ n ⋅n −3
所以cos= 1 2 = ,
1 2 ⃗ ⃗ √12+4λ2
|n |⋅|n |
1 2
π
因为平面EBD与平面ABB A 的夹角为 ,
1 1 4
−3 √2 √6
所以 | |= ,解得λ=± ,
√12+4λ2 2 2
第 页,共 页
12 1√6
又因为0≤λ≤1,所以λ=± 舍去,
2
π
所以线段C D 上不存在点E使得平面EBD与平面ABB A 的夹角为 .
1 1 1 1 4
第 页,共 页
13 1