山东名校考试联盟2024-2025学年高三上学期期中检测数学试题+答案_2024-2025高三（6-6月题库）_2024年11月试卷_11152025届山东名校考试联盟高三上学期期中检测（全科）

{{##{{QQQQAABBSSYYaYAogxggAAQgQ0hgSBAACAKA5hrCQQQQHXyCCCgmgKQQkkogCAhAJCWSggEGAxQACAGAOMAAwADBSCBRFFIAFBIAA=A}#=}}#}{{##{{QQQQAABBSSYYaYAogxggAAQgQ0hgSBAACAKA5hrCQQQQHXyCCCgmgKQQkkogCAhAJCWSggEGAxQACAGAOMAAwADBSCBRFFIAFBIAA=A}#=}}#}{{##{{QQQQAABBSSYYaYAogxggAAQgQ0hgSBAACAKA5hrCQQQQHXyCCCgmgKQQkkogCAhAJCWSggEGAxQACAGAOMAAwADBSCBRFFIAFBIAA=A}#=}}#}{{##{{QQQQAABBSSYYaYAogxggAAQgQ0hgSBAACAKA5hrCQQQQHXyCCCgmgKQQkkogCAhAJCWSggEGAxQACAGAOMAAwADBSCBRFFIAFBIAA=A}#=}}#}山东名校考试联盟 高三阶段性测试数学参考答案 一、选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一 项是符合题目要求的。 题号 1 2 3 4 5 6 7 8 答案 C B D B A C D D 8.【解析】根据 f(x+2)+ f(x)= f(4)，以 - 1 - x + 2 代换 x 得： f(x+4)+ f(x+2)= f(4)， 所以 f(x+4)= f(x)，可知函数 f ( x ) 的周期为4， 因为 f(2x+1)是 R 上的奇函数，所以 f(−2x+1)+ f(2x+1)=0，即 f ( x ) 关于点(1,0)对称， 1 3 5 7 5 1 于是 f( )+ f( )=0， f( )+ f( )= f( )+ f(− )=0， 2 2 2 2 2 2 由 f(x+4)+ f(x+2)= f(4)，取 x = 0 得 + = f ( 4 ) f ( 2 ) f ( 4 ) ，即 f ( 2 ) = 0 ， 则 f(4)= f(0)=−f(2)=0，因此 f ( x + 2 ) + f ( x ) = 0 ，取 x = 3 2 ，得 f ( 3 2 ) + f ( 7 2 ) = 0 ， 1 3 5 7 1 3 5 7 3 7 于是 f( )+2f( )+3f( )+4f( )=[f( )+ f( )]+3[f( )+ f( )]+ f( )+ f( )=0， 2 2 2 2 2 2 2 2 2 2 5 1 9 1 1 因此，k(k− )=5f( )=5f(4+ )=5f( )=5. 2 2 2 2 k=1 二、选择题：本题共3小题，每小题6分，共18分．在每小题给出的四个选项中，有多项 符合题目要求．全部选对的得6分，部分选对的得部分分，有选错的得0分。 题号 9 10 11 答案 ABD AC BCD 10. 【解析】外心为外接圆圆心，也为三边中垂线的交点. 取AB的中点D，因为(OA+OB) AB=2OD AB=0，A,C对； 1 2 1 2 因为OA BC =OA (AC−AB) =OA AC−OA AB =− AC + AB =6，所以B错； 2 2 由奔驰定理得(sin2A)OA+(sin2B)OB+(sin2C)OC =0，D错. 答案为：AC. 11. 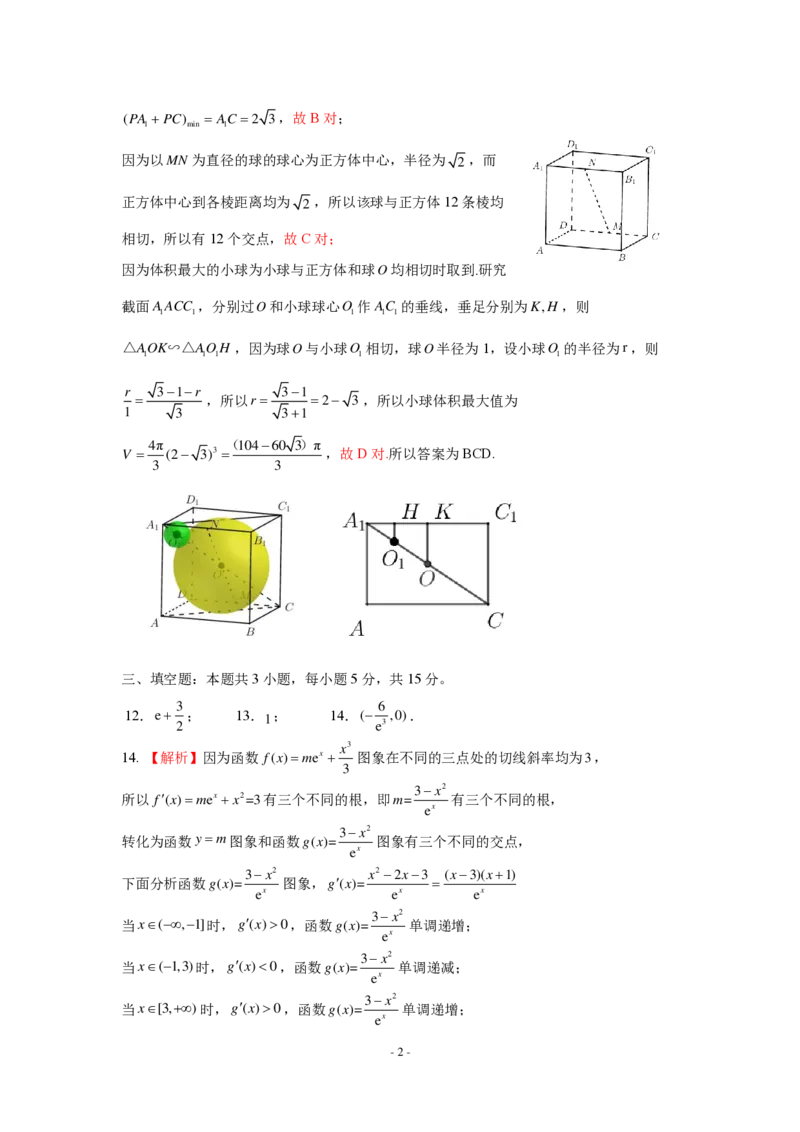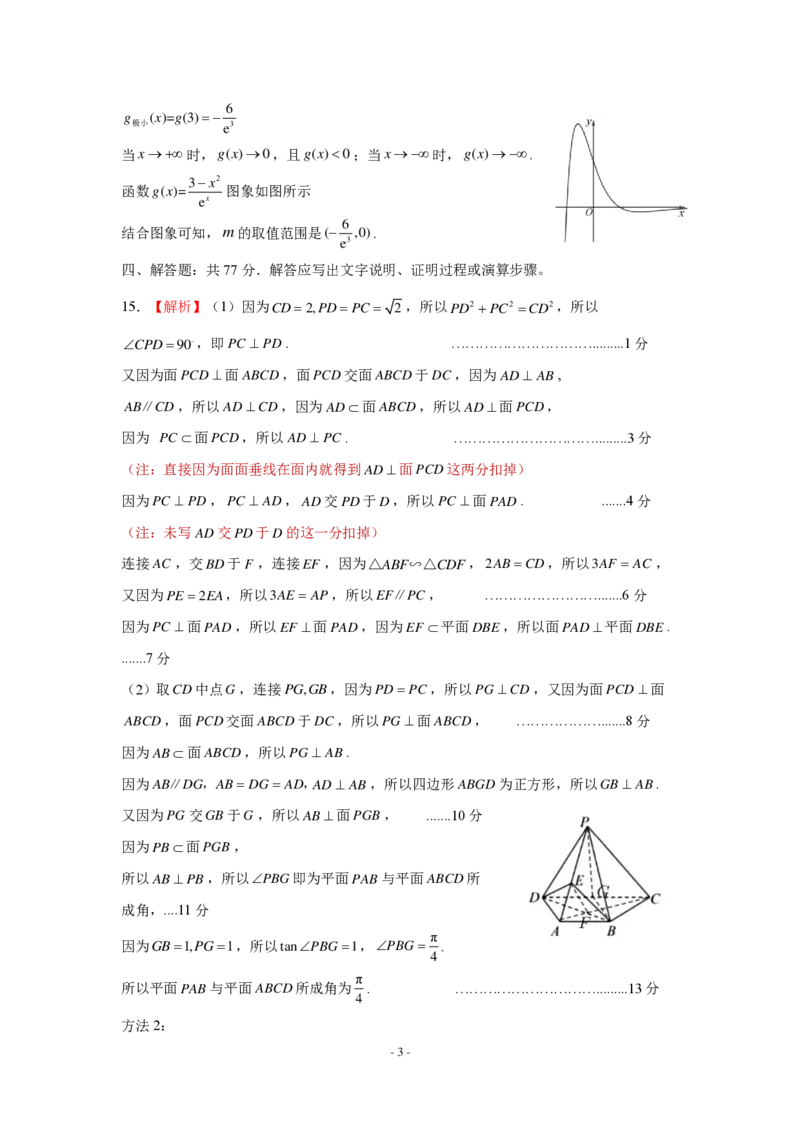【解析】取AB中点G ，所以APB=2GPB，因为△GPB为直角三角形， 当P在 运动中时，PG[ 2,2]，GB=1PG，所以GPB45 ，APB90 ，故A错； 由对称性得PD=PC，即求PA +PD=PA +PC，在面CDAB 中， 1 1 1 1 {{##{{QQQQAABBSSYYaYAogxggAAQgQ0hgSBAACAKA5hrCQQQQHXyCCCgmgKQQkkogCAhAJCWSggEGAxQACAGAOMAAwADBSCBRFFIAFBIAA=A}#=}}#}- 2 - ( P A 1 + P C ) m in = A C1 = 2 3 ，故B对； 因为以MN 为直径的球的球心为正方体中心，半径为 2 ，而 正方体中心到各棱距离均为 2 ，所以该球与正方体12条棱均 相切，所以有12个交点，故C对； 因为体积最大的小球为小球与正方体和球 O 均相切时取到.研究 截面 A 1 A C C 1 ，分别过 O 和小球球心 O 1 作AC 的垂线，垂足分别为 1 1 K , H ，则 △ A O1 K ∽ △ A O1 1 H ，因为球 O 与小球 O 1 相切，球 O 半径为1，设小球 O 1 的半径为 r ，则 r 1 = 3 − 1 3 − r 3−1 ，所以r= =2− 3，所以小球体积最大值为 3+1 V = 4 π 3 ( 2 − 3 ) 3 = （ 1 0 4 − 6 3 0 3 ） π ，故D对.所以答案为BCD. 三、填空题：本题共3小题，每小题5分，共15分。 12． e + 3 2 ； 13． 1 ； 14． ( − 6 3 e , 0 ) ． x3 14. 【解析】因为函数 f(x)=mex + 图象在不同的三点处的切线斜率均为3， 3 所以 f ( x ) = m e x + x 2 = 3 有三个不同的根，即 m = 3 − e x x 2 有三个不同的根， 转化为函数 y = m 3−x2 图象和函数g(x)= 图象有三个不同的交点， ex 下面分析函数 g ( x ) = 3 − e x x 2 图象， g ( x ) = x 2 − 2 e x x − 3 = ( x − 3 ) e ( x x + 1 ) 3−x2 当x(−,−1]时，g(x)0，函数g(x)= 单调递增； ex 当x(−1,3)时， g ( x )  0 3−x2 ，函数g(x)= 单调递减； ex 3−x2 当x[3,+)时，g(x)0，函数g(x)= 单调递增； ex {{##{{QQQQAABBSSYYaYAogxggAAQgQ0hgSBAACAKA5hrCQQQQHXyCCCgmgKQQkkogCAhAJCWSggEGAxQACAGAOMAAwADBSCBRFFIAFBIAA=A}#=}}#}- 3 - g 极 小 ( x ) = g ( 3 ) = − 6 3 e 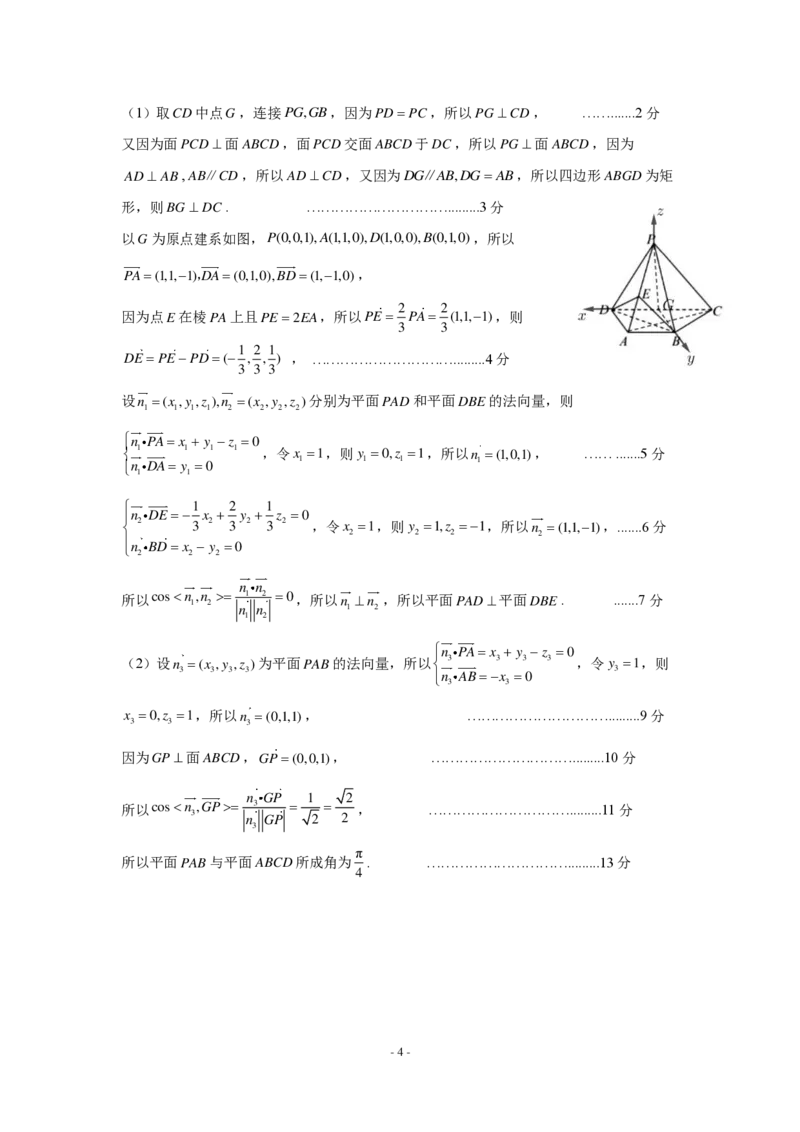当 x → +  时， g ( x ) → 0 ，且 g ( x )  0 ；当 x → −  时， g ( x ) → −  . 函数 g ( x ) = 3 − e x x 2 图象如图所示 结合图象可知， m 的取值范围是 ( − 6 3 e , 0 ) . 四、解答题：共77分．解答应写出文字说明、证明过程或演算步骤。 15．【解析】（1）因为CD=2,PD=PC= 2，所以 P D 2 + P C 2 = C D 2 ，所以 CPD=90 ，即 P C ⊥ P D . ………………………….........1分 又因为面 P C D ⊥ 面 A B C D ，面 P C D 交面ABCD于 D C ，因为AD⊥ AB, A B ∥ C D ，所以 A D ⊥ C D ，因为 A D  面ABCD，所以AD⊥面PCD， 因为 P C  面 P C D ，所以 A D ⊥ P C . ………………………….........3分 （注：直接因为面面垂线在面内就得到AD⊥面 P C D 这两分扣掉） 因为 P C ⊥ P D ， P C ⊥ A D ， A D 交 P D 于 D ，所以 P C ⊥ 面 P A D . .......4分 （注：未写AD交 P D 于 D 的这一分扣掉） 连接 A C ，交 B D 于 F ，连接 E F ，因为 △ A B F ∽ △ C D F ， 2 A B = C D ，所以 3 A F = A C ， 又因为PE=2EA，所以 3 A E = A P ，所以 E F ∥ P C ， …………………….......6分 因为 P C ⊥ 面 P A D ，所以EF ⊥面 P A D ，因为EF 平面 D B E ，所以面PAD⊥平面DBE. 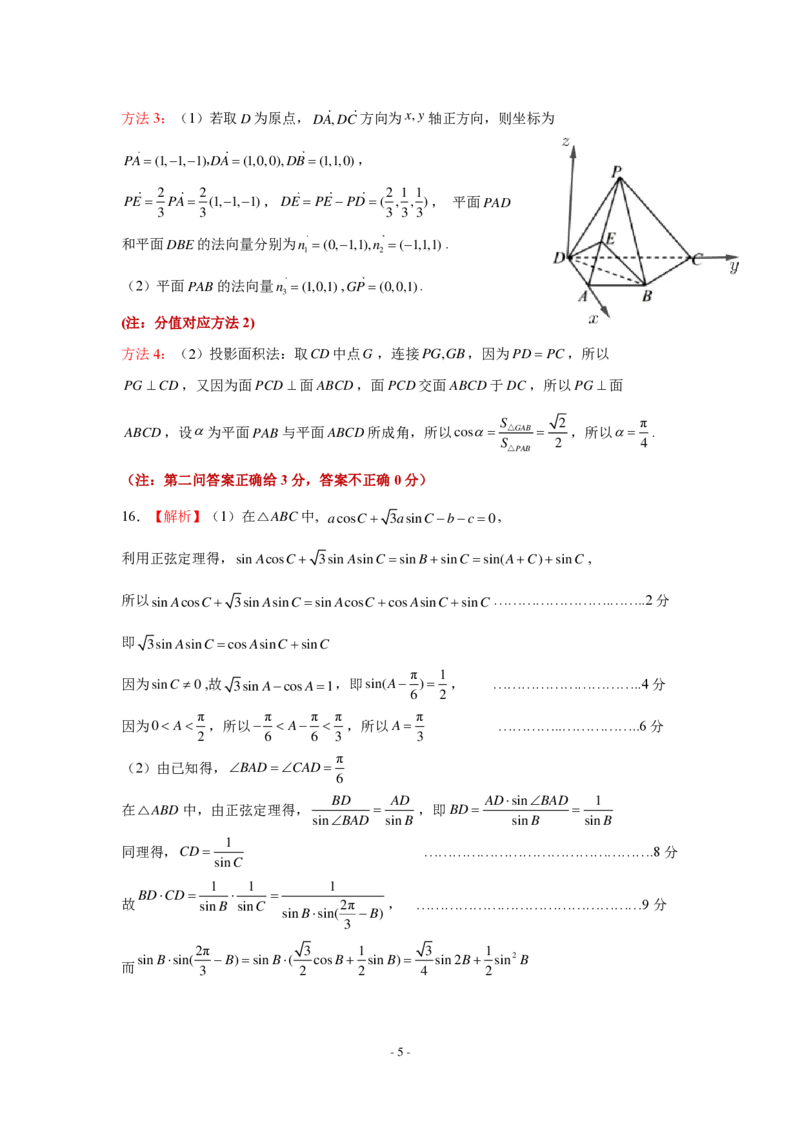.......7分 （2）取CD中点G ，连接 P G , G B ，因为PD=PC，所以PG⊥CD，又因为面 P C D ⊥ 面 ABCD，面 P C D 交面ABCD于DC，所以PG⊥面ABCD， ……………….......8分 因为 A B  面 A B C D ，所以 P G ⊥ A B . 因为 A B ∥ D G ， A B = D G = A D ， AD⊥ AB，所以四边形ABGD为正方形，所以GB⊥ AB. 又因为 P G 交 G B 于 G ，所以 A B ⊥ 面 P G B ， .......10分 因为PB面PGB， 所以 A B ⊥ P B ，所以PBG即为平面 P A B 与平面ABCD所 成角，....11分 因为 G B = 1 , P G = 1 ，所以 ta n  P B G = 1 π ，PBG= . 4 π 所以平面PAB与平面ABCD所成角为 . ………………………….........13分 4 方法2： {{##{{QQQQAABBSSYYaYAogxggAAQgQ0hgSBAACAKA5hrCQQQQHXyCCCgmgKQQkkogCAhAJCWSggEGAxQACAGAOMAAwADBSCBRFFIAFBIAA=A}#=}}#}（1）取 - 4 - C D 中点 G ，连接 P G , G B ，因为 P D = P C ，所以 P G ⊥ C D ， …….......2分 又因为面 P C D ⊥ 面 A B C D ，面 P C D 交面ABCD于 D C ，所以PG⊥面 A B C D ，因为 AD⊥ AB,AB∥CD，所以 A D ⊥ C D ，又因为 D G ∥ A B , D G = A B ，所以四边形ABGD为矩 形，则 B G ⊥ D C . ………………………….........3分 以 G 为原点建系如图，P(0,0,1),A(1,1,0),D(1,0,0),B(0,1,0)，所以 P A = (1 ,1 , − 1 ，) D A = ( 0 ,1 , 0 ) , B D = (1 , − 1 , 0 ) ， 因为点E在棱PA上且PE=2EA，所以 P E = 2 3 P A = 2 3 (1 ,1 , − 1 ) ，则 D E = P E − P D = ( − 1 3 , 2 3 , 1 3 ) ， ………………………….........4分 设 n 1 = ( x 1 , y 1 , z 1 ) , n 2 = ( x 2 , y 2 , z 2 ) 分别为平面 P A D 和平面 D B E 的法向量，则  n n 1 1 P D A A = = x 1 y 1 + = y 1 0 − z 1 = 0 ，令 x 1 = 1 ，则 y 1 = 0 , z 1 = 1 ，所以 n 1 = (1 , 0 ,1 ) ， …… .......5分  n n 2 2 D B E D = = − x 1 3 2 − x 2 y + 2 = 2 3 0 y 2 + 1 3 z 2 = 0 ，令 x 2 = 1 ，则 y 2 = 1 , z 2 = − 1 ，所以 n 2 = (1 ,1 , − 1 ) ，.......6分 所以 c o s  n 1 , n 2  = n n 1 1 n n 2 2 = 0 ，所以 n 1 ⊥ n 2 ，所以平面 P A D ⊥ 平面 D B E . .......7分 （2）设 n 3 = ( x 3 , y 3 , z 3 ) 为平面 P A B 的法向量，所以  n n 3 3 P A A B = = x − 3 x + 3 y = 3 0 − z 3 = 0 ，令 y 3 = 1 ，则 x =0,z =1，所以n =(0,1,1)， ………………………….........9分 3 3 3 因为 G P ⊥ 面ABCD，GP=(0,0,1)， ………………………….........10分 所以 c o s  n 3 , G P  = n n 3 3 G G P P = 1 2 = 2 2 ， ………………………….........11分 π 所以平面PAB与平面ABCD所成角为 . ………………………….........13分 4 {{##{{QQQQAABBSSYYaYAogxggAAQgQ0hgSBAACAKA5hrCQQQQHXyCCCgmgKQQkkogCAhAJCWSggEGAxQACAGAOMAAwADBSCBRFFIAFBIAA=A}#=}}#}方法3：（1）若取 - 5 - D 为原点， D A , D C 方向为 x , y 轴正方向，则坐标为 P A = (1 , − 1 , − 1 ，) D A = (1 , 0 , 0 ) , D B = (1 ,1 , 0 ) ， P E = 2 3 P A = 2 3 (1 , − 1 , − 1 ) 2 1 1 ，DE=PE−PD=( , , )， 平面 3 3 3 P A D 和平面 D B E 的法向量分别为 n 1 = ( 0 , − 1 ,1 ) , n 2 = ( − 1 ,1 ,1 ) . （2）平面 P A B 的法向量 n 3 = (1 , 0 ,1 ) , G P = ( 0 , 0 ,1 ) . (注：分值对应方法2) 方法4：（2）投影面积法：取 C D 中点 G ，连接 P G , G B ，因为 P D = P C ，所以 PG⊥CD，又因为面PCD⊥面ABCD，面PCD交面ABCD于DC，所以PG⊥面 A B C D ，设为平面 P A B 与平面 A B C D 所成角，所以 c o s S S G P A A B B 2 2  = △ △ = ，所以 π 4  = . （注：第二问答案正确给3分，答案不正确0分） 16．【解析】（1）在△ABC中, a c o s C + 3 a s in C − b − c = 0 , 利用正弦定理得， s in A c o s C + 3 s in A s in C = s in B + s in C = s in ( A + C ) + s in C , 所以 s in A c o s C + 3 s in A s in C = s in A c o s C + c o s A s in C + s in C …………………….……..2分 即 3sinAsinC=cosAsinC+sinC 因为 s in C  0 ,故 3 s in A − c o s A = 1 π 1 ，即sin(A− )= ， …………………………..4分 6 2 因为 0  A  π 2 π π π π ，所以−  A−  ，所以A= …………..……………..6分 6 6 3 3 （2）由已知得，  B A D =  C A D = π 6 在△ABD中，由正弦定理得， s in B  D B A D = s A in D B ，即 B D = A D  s s in in  B B A D = s 1 in B 同理得， C D = s 1 in C ………………………………………….8分 1 1 1 BDCD=  = 故 sinB sinC 2π ， …………………………………………9分 sinBsin( −B) 3 2π 3 1 3 1 sinBsin( −B)=sinB( cosB+ sinB)= sin2B+ sin2B 而 3 2 2 4 2 {{##{{QQQQAABBSSYYaYAogxggAAQgQ0hgSBAACAKA5hrCQQQQHXyCCCgmgKQQkkogCAhAJCWSggEGAxQACAGAOMAAwADBSCBRFFIAFBIAA=A}#=}}#}- 6 - = 4 3 s in 2 B − 1 4 c o s 2 B + 1 4 = 1 2 s in ( 2 B − π 6 ) + 1 4 ……………………….12分 因为锐角 △ A B C 中， 0  C = 2 π 3 − B  π 2 ，所以 π 6  B  π 2 ………………..….13分 π π 5π π 1 1 π 1 1 3 故2B− ( , ),sin(2B− )( ,1], sin(2B− )+ ( , ] 6 6 6 6 2 2 6 4 2 4 所以 B D  C D 的取值范围为 [ 4 3 , 2 ) . ………………………………………….15分 17．【解析】（1）由题意n=7，且每一行都成等差数列则有： a 1 1 + a 1 2 + + a 1 7 = 7 a 1 4 ， ………………………………………….2分 a 2 1 + a 2 2 + + a 2 7 = 7 a 2 4 ， ， a 7 1 + a 7 2 + + a 7 7 = 7 a 7 4 ， 则有 M = 7  ( a 1 4 + a 2 4 + + a 7 4 ) ， ………………………………………….4分 又因为每一列成等差数列，故有 a 1 4 + a 2 4 + + a 7 4 = 7 a 4 4 = 3 5 ， 即 M = 7  3 5 = 2 4 5 ． ……………………………………….6分 （2）由题意每一行均为等差数列，设第二行的公差为d ， 则有 2 d = a 2 5 − a 2 3 = 8 ，故 d = 4 ， ……………………………………….7分 从而可得第二行的通项公式 a 2 n = a 2 3 + ( n − 3 )  4 = 4 n − 2 ，……………………………….8分 所以 a 2 6 = 2 2 ，又因为每一列均为公比为 q 的等比数列，且a =88 46 又因为 a ij  0 ，故q=2， …………………………………….10分 即有 a m n = a 2 n  q m − 2 = ( 4 n − 2 )  2 m − 2 = ( 2 n − 1 )  2 m − 1 ，从而有 a n n = ( 2 n − 1 )  2 n − 1 ， …….12分 故S =a +a + +a =120 +321+522 + +(2n−3)2n−2 +(2n−1)2n−1 11 22 nn 2 S = 1  2 1 + 3  2 2 + 5  2 3 + + ( 2 n − 3 )  2 n − 1 + ( 2 n − 1 )  2 n ………………….13分 所以 − S = 1 + 2 ( 2 1 + 2 2 + +  2 n − 1 ) − ( 2 n − 1 )  2 n …………………………….14分 即 S = ( 2 n − 3 )  2 n + 3 ． …………………………….15分 18．【解析】（1）由题意可知 f ( 0 ) = 0 ， …………………………..1分 f(x)=3ax2+2cosx−1，则 f(0)=1， …………………………..2分 故曲线y= f(x)在点(0, f(0))处的切线方程为y= x． …………………………..3分 {{##{{QQQQAABBSSYYaYAogxggAAQgQ0hgSBAACAKA5hrCQQQQHXyCCCgmgKQQkkogCAhAJCWSggEGAxQACAGAOMAAwADBSCBRFFIAFBIAA=A}#=}}#}（2）当 - 7 - a = 1 时， f ( x ) = x 3 + 2 s in x − x ．则 f ( x ) = 3 x 2 + 2 c o s x − 1 ． 当0 x1时， c o s x c o s 1 c o s 3 1 2    = ，此时 f ( x ) = 3 x 2 + 2 c o s x − 1 2 c o s x − 1  0 ． …………………………..5分 当x 1时， f ( x ) = 3 x 2 + 2 c o s x − 1 3 x 2 − 2 − 1 0 ． 故 f(x)0在 [ 0 , +  ) 上恒成立． …………………………..7分 再由 f ( − x ) = 3 ( − x ) 2 + 2 c o s ( − x ) − 1 = 3 x 2 + 2 c o s x − 1 = f ( x ) 可知 f ( x ) 为偶函数，于是 f ( x )  0 在 R 上恒成立．故 f ( x ) 在 R 上单调递增． …………………………..8分 （3）当x=0时， f ( x ) = 0 符合题意． …………………………..9分 当x0时，由 f ( x ) 0 可得 a x − 2 x s 3 in x ． ………………………….11分 x−2sinx 令F(x)= ，则 x3 F  ( x ) = 2 ( 3 s in x − x x 4 − x c o s x ) ． 令G(x)=3sinx−x−xcosx，则 G ( x ) = x s in x + 2 c o s x − 1 ． 令H(x)=xsinx+2cosx−1，则 H ( x ) = x c o s x − s i n x ． 令K(x)=xcosx−sinx， 当0x π时， K ( x ) = − x s i n x  0 ，故 K ( x ) 在 ( 0 , π ] 上单调递减． 又K(0)=0，则此时 K ( x )  0 ．故 H ( x ) 在 ( 0 , π ] 上单调递减． 因为H(0)=10，H(π)=−30，则存在 x 0  ( 0 , π ) ，使得 H ( x 0 ) = G ( x 0 ) = 0 ，于是 G ( x ) 在(0,x )上单调递增，在 0 ( x 0 , π ] 上单调递减．由于G(0)=0，G(π)=0，则当x(0,π]时， G(x) 0，此时F(x) 0．因此 F ( x ) 在(0,π]上单调递增． 故当 x  ( 0 , π ] 时， F ( x ) F ( π ) = 1 π 2 ． ………………………….14分 x3 令L(x)=2sinx+ −x,xπ，则 π2 L ( x ) = 2 c o s x + 2 3 x 2 π − 1 ． 当xπ时， L  ( x ) = 2 c o s x + 2 3 x 2 π − 1  − 2 + 3 π π 2 2 − 1 = 0 ，则L(x)在 ( π , +  ) 上单调递增，此时 L ( x )  L ( π ) = 0 x−2sinx 1 ．故当x(π,+)时，F(x)=  ． ……………………….16分 x3 π2 x−2sinx 1 故F(x)= 在 x3 π2 ( 0 , +  ) 上恒成立．  1  因此a的取值范围为  π2 ,+  ． ………………………….17分 {{##{{QQQQAABBSSYYaYAogxggAAQgQ0hgSBAACAKA5hrCQQQQHXyCCCgmgKQQkkogCAhAJCWSggEGAxQACAGAOMAAwADBSCBRFFIAFBIAA=A}#=}}#}19．【解析】（1） - 8 - T 1 不是“理想集”， T 2 是“理想集”． ………………………….2分 （注：答对一个给一分） （2）共16个“理想集”. …………………………..4分 若n=1，有 S = { 0 ,1 , 2 , 3 , 4 , 5 } ． 当 | T |= 3 时，若 a = 0 ，则 b 1 ，由 c + 2 a  3 b 可知 c  3 b 3 ，故(b,c)=(1,4)或 (1 , 5 ) ； 若a=1，则 b 2 ，由c+2a3b可知c+23b 6，则 4  c 5 ，故 ( b , c ) = ( 2 , 5 ) ． 故含有三个元素的“理想集” T = { 0 ,1 , 4 } ,{ 0 ,1 , 5 } 或{1,2,5}，共3个．…………………..6分 当|T |=4时，T ={0,1,2,4},{0,1,3,4}， { 0 ,1 , 2 , 5 } ,{ 0 ,1 , 3 , 5 } ,{ 0 ,1 , 4 , 5 } ，{1,2,3,5}，或 { 1 , 2 , 4 , 5 } ，共7个． 当 | T |= 5 时，T ={0,1,2,3,4}， { 0 ,1 , 2 , 3 , 5 } ， { 0 ,1 , 2 , 4 , 5 } ,{ 0 ,1 , 3 , 4 , 5 } ， { 1 , 2 , 3 , 4 , 5 } ，共5个． 当 | T |= 6 时，T ={0,1,2,3,4,5}，共1个． 综上所述，所有“理想集” T 的个数为16个分别为： { 0 ,1 , 4 } ,{ 0 ,1 , 5 } ，{1,2,5}， { 0 ,1 , 2 , 4 } ， { 0 , 1 , 3 , 4 } ， { 0 ,1 , 2 , 5 } ,{ 0 ,1 , 3 , 5 } ,{ 0 ,1 , 4 , 5 } ， { 1 , 2 , 3 , 5 } ， { 1 , 2 , 4 , 5 } ， { 0 ,1 , 2 , 3 , 4 } ， { 0 ,1 , 2 , 3 , 5 } ， { 0 ,1 , 2 , 4 , 5 } ,{ 0 ,1 , 3 , 4 , 5 } ， { 1 , 2 , 3 , 4 , 5 } ， { 0 ,1 , 2 , 3 , 4 , 5 } ． …………………………..8分 （注：没有步骤不扣分，缺少或错误均不给分） （3）若 | T |= 4 n + 2 ，记 T = { x 1 , x 2 , , x 4 n + 2 } 且 0 x 1  x 2   x 4 n + 2 5 n ． …………..9分 利用反证法，假设对于 T 中任意三个元素 a , b , c ( a  b  c ) ，均有c+2a 3b，………..10分 则3x x +2x ， i+1 4n+2 i i = 1 , 2 , , 4 n + 1 ． …………………………..11分 记y =x −x 0，于是 i 4n+2 i y i+ 1 2 3 y i ， …………………………..12分 则 y 4 n + 1 2 3 y 4 n  2 3  2 y 4 n − 1  2 3  4 n y 1 ． …………………………..14分 因此 1 y 4 n + 1  2 3  4 n ( x 4 n + 2 − x 1 )  1 8 6 1  n ( 5 n − 0 ) =  8 8 0 1  n  1 ，矛盾．……………………..16分 故集合 T 必为“理想集”． …………………………..17分 {{##{{QQQQAABBSSYYaYAogxggAAQgQ0hgSBAACAKA5hrCQQQQHXyCCCgmgKQQkkogCAhAJCWSggEGAxQACAGAOMAAwADBSCBRFFIAFBIAA=A}#=}}#}