文档内容
“宁化、永安、尤溪、大田、沙县一中”五校协作
2023—2024 学年高三 11 月联考
高三数学试题
命题人:尤溪一中 王伟荣 审题学校:永安、宁化、大田、沙县一中
(考试时间:120分钟 总分150分)
试卷分第I卷(选择题)和第II卷(非选择题)两部分
第I卷(选择题,共60分)
一.选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目
要求的.
1.设全集 ,若集合 满足 ,则( )
A. B. C. D.
2.复数 ,则 ( )
A. B. C. D.
3.已知向量 , 满足 , , ,则 与 的夹角为( )
A. B. C. D.
4.若偶函数 满足 ,当 时, ,则 ( )
A. B. C. D.
5.“中国剩余定理”又称“孙子定理”,1852年英国来华传教士伟烈亚利将《孙子算法》中“物
不知数”问题的解法传至欧洲.1874年,英国数学家马西森指出此法符合1801年由高斯得出
的关于同余式解法的一般性定理,因而西方称之为“中国剩余定理”,“中国剩余定理”讲
第 1 页 共 5 页
学科网(北京)股份有限公司的是一个关于整除的问题,现有这样一个整除问题:将1至2022这2022个数中,能被5除余
1且被7除余1的数按由小到大的顺序排成一列,构成数列 ,则此数列的项数为( )
A.58 B.57 C.56 D.55
6.下列说法正确的是( )
A.随机变量 ,则
B.若随机变量 , ,则
C.从装有2个红球和2个黑球的口袋内任取2个球,至少有一个黑球与至少有一个红球是两个互
斥而不对立的事件
D.从除颜色外完全相同的 个红球和 个白球中,一次摸出 个球,则摸到红球的个数服从超
几何分布;
7.已知函数 ,则 在 上不单调的一个充分不必要条件是( )
A. B. C. D.
8.已知在正三棱锥 中, 为 的中点, ,则正三棱锥 的表面积与该
三棱锥的外接球的表面积的比为( )
A. B. C. D.
二.多选题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部
选对的得5分,部分选对的得2分,有选错的得0分.
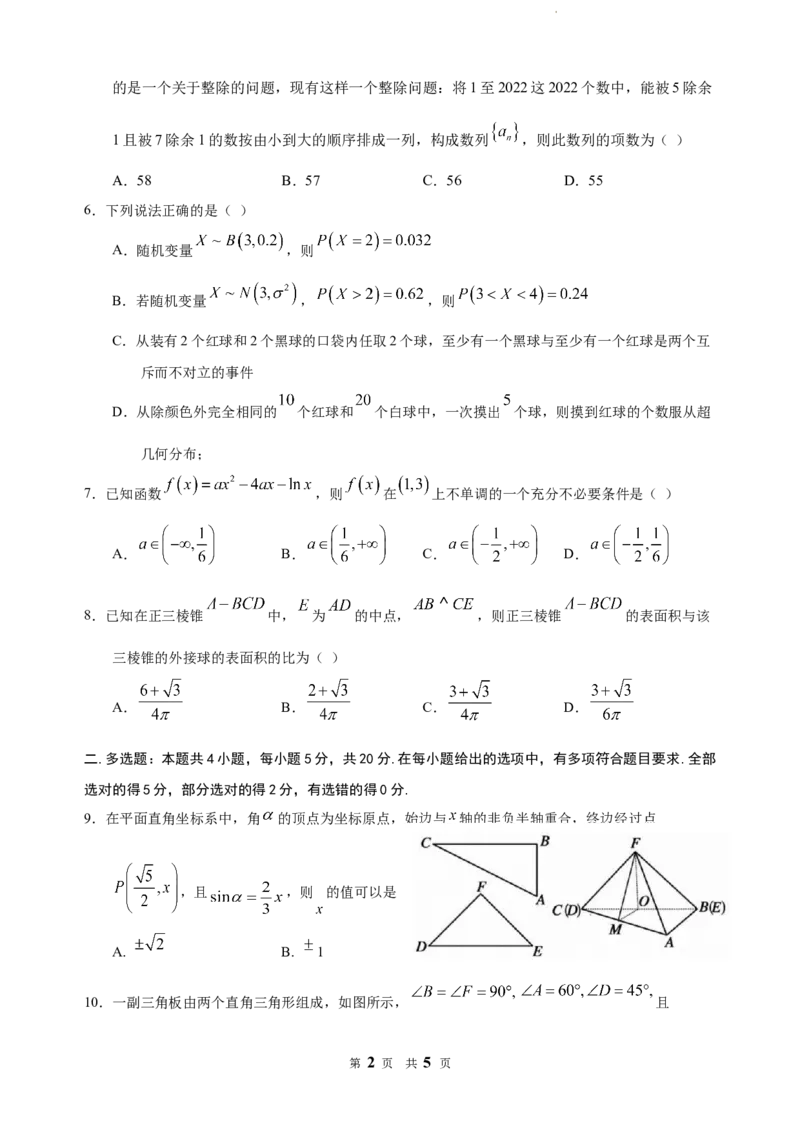
9.在平面直角坐标系中,角 的顶点为坐标原点,始边与 轴的非负半轴重合,终边经过点
,且 ,则 的值可以是( )
A. B. 1 C. 0 D. 2
10.一副三角板由两个直角三角形组成,如图所示, 且
第 2 页 共 5 页
学科网(北京)股份有限公司,现将两块三角板拼接在一起,得到三棱锥 ,取 和 中点 、 ,则
下列判断中正确的是( )
A.直线 面
B.三棱锥 体积为定值.
C. 与面 所成的角为定值
D.设面 面 ,则 ∥
11.已知 ,则实数 满足( )
A. B. C. D.
12.数列 的前n项和为 , ,且当 时, .则下列结论正确的是( )
A. 是等差数列 B. 既有最大值也有最小值.
C. D. 若 ,则 .
第II卷(非选择题,共90分)
三.填空题:本题共4小题,每小题5分,共20分.
13.等比数列 的前 项和 ,若 , , , ,则 ___ .
14.楼道里有12盏灯,为了节约用电,需关掉3盏,关掉的灯不能相邻,则关灯方案有___ 种.
15.已知函数 ,则不等式 的解集是___ __.
16.已知函数 和 ,若总存在两条不同的直线与函数 和 图象都
第 3 页 共 5 页
学科网(北京)股份有限公司相切,则实数 的取值范围为___ __.
四.解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分10分)
在 中,角 所对的边分别是 .已知 .
(1)若 ,求 ;
(2)求 的取值范围.
18.(本小题满分12分)
已知函数 的最大值为 ,其相邻两个零点之间
的距离为 ,且 的图象关于直线 对称.
(1)当 时,求函数 的递增区间.
(2)若对任意的 恒成立,求实数 的最小正值.
19.(本小题满分12分)
等差数列 满足 , .数列 的前n项和 满足 .
(1)求数列 和 的通项公式;
(2)对于集合 , ,定义集合 且 .设数列 和 中的所有项分别
构成集合A,B,将集合 的所有元素按从小到大依次排列构成一个新数列 ,求数列
的前 项和 .
20.(本小题满分12分)
E
F
第 4 页 共 5 页
学科网(北京)股份有限公司
DE
F
D
在多面体 中, ,且 ,
,
(1)证明: ;
(2)若 ,求直线 与平面 所成角的正弦值.
21.(本小题满分12分)
小芳、小明两人各拿两颗质地均匀的骰子做游戏,规则如下:若掷出的点数之和为 的倍数,则
由原投掷人继续投掷;若掷出的点数之和不是 的倍数,则由对方接着投掷.
(1)规定第 次从小明开始.
(ⅰ)求前 次投掷中小明恰好投掷 次的概率;
(ⅱ)设游戏的前 次中,小芳投掷的次数为 ,求随机变量 的分布列与期望.
(2)若第 次从小芳开始,求第 次由小芳投掷的概率 .
22.(本小题满分12分)
已知函数 , .
(1)若 在 处取得极值,求 的值;
(2)设 ,讨论函数 的单调性;
(3)当 时,若存在正实数 , 满足 ,求证:
第 5 页 共 5 页
学科网(北京)股份有限公司