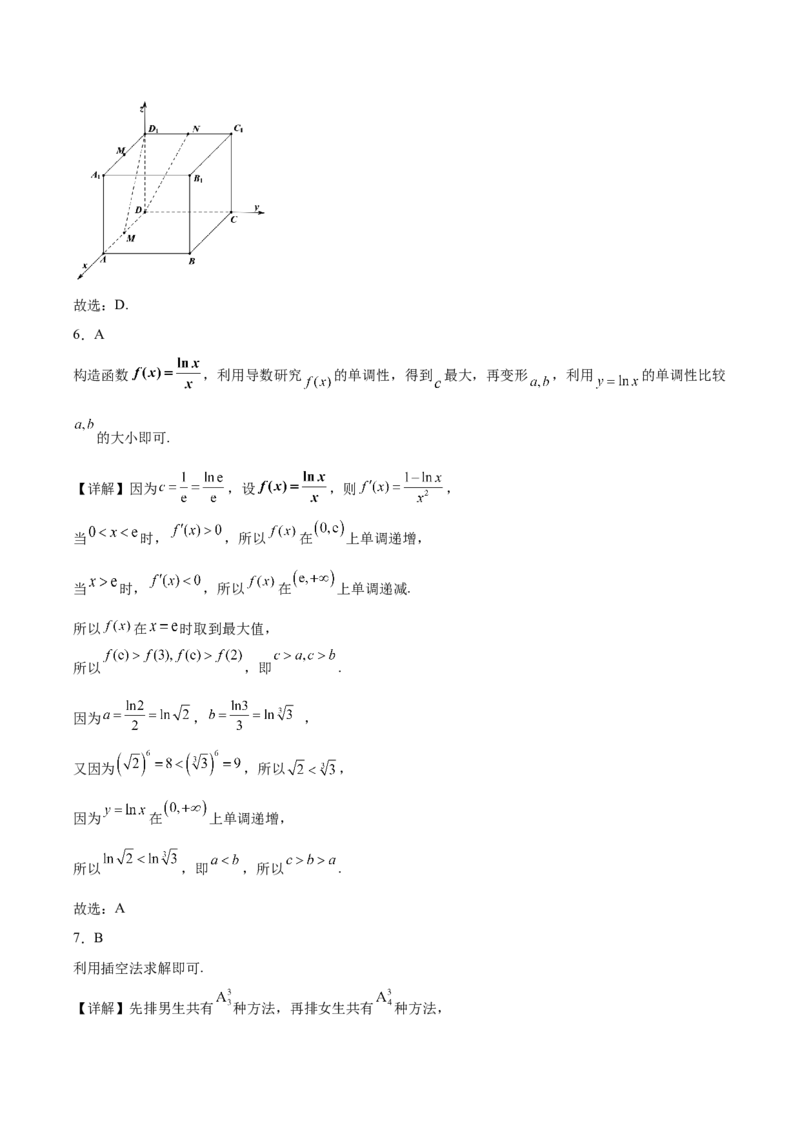文档内容
江苏扬州市邗江区2024-2025学年高二下学期期中考试数学试卷
一、单选题
1.已知向量 ,满足 ,则 ( )
A. B.1 C. D.2
2.已知函数 ,则 ( )
A. B. C. D.
3.如图,空间四边形OABC中, , , ,且 , ,则 等于
( )
A. B. C. D.
4.函数 的单调递减区间是( )
A. B. C. D.
5.在正方体 中, 是 的中点, 是 的中点,则异面直线 与 所成角的
余弦值为( )
A. B. C. D.
6.已知 ,则( )
A. B.
C. D.
7.有3名男生和3名女生排成一排,女生不能相邻的不同排法有( )
A.72种 B.144种 C.108种 D.288种8.设函数 是定义在 上的奇函数, 为其导函数.当 时, , ,则
不等式 的解集为( )
A. B.
C. D.
二、多选题
9.已知A,B,C,D是空间直角坐标系 中的四点,P是空间中任意一点,则( )
A.若 与 关于平面 对称,则
B.若 ,则A,B,C,D共面
C.若 ,则A,B,C,D共面
D.若 三点共线,则
10.在 件产品中,有 件合格品, 件不合格品,从这 件产品中任意抽出 件,则( )
A.抽出的 件中恰好有 件是不合格品的抽法有 种
B.抽出的 件中恰好有 件是不合格品的抽法有 种
C.抽出的 件中至少有 件是不合格品的抽法有 种
D.抽出的 件中至少有 件是不合格品的抽法有 种
11.设函数 ,则( )
A.当 时, 有两个零点
B.当 时, 是 的极大值点C.当 时,点 为曲线 的对称中心
D.当 时, 在区间 上单调递增
三、填空题
12.若 ,则 的值为 .
13.函数 的极值是 .
14.在平行六面体 中,已知底面四边形 为矩形, , ,
,则 .
四、解答题
15.已知函数 ,且 .
(1)求 的值;
(2)求函数 的图象在点 处的切线方程.
16.用 五个数字,问:
(1)可以组成多少个无重复数字的四位密码?
(2)可以组成多少个无重复数字的四位数?
(3)可以组成多少个十位数字比个位数字大的无重复数字的四位偶数?
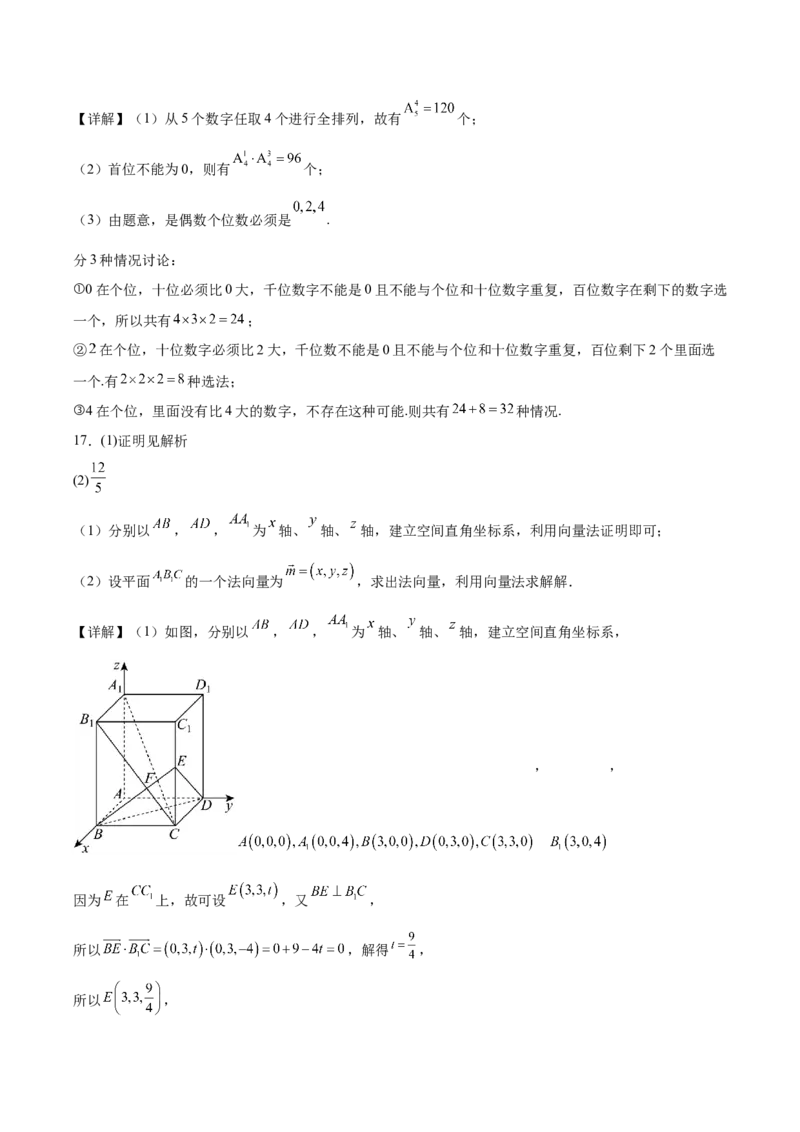
17.如图,长方体 中, , . 是棱 上一点,且 ,交 于点 .
(1)求证: 平面 ;(2)求点 到平面 的距离.18.如图,在空间几何体ABCDPE中,正方形PDCE所在平面垂直于梯形ABCD所在平面 ,
, ,点F在线段AP上,
(1)求二面角 的正弦值;
(2) 为线段 上一点,若直线BQ与平面BCP所成角的正弦值为 ,求线段 的长.
19.已知函数 .
(1)求 的最小值;
(2)若 对任意的 恒成立,求实数 的取值范围;
(3)若 是函数 的极值点,求证: .
题号 1 2 3 4 5 6 7 8 9 10
答案 D C C A D A B C BD ACD
题号 11
答案 ACD
1.D
根据空间向量数量积的坐标运算即可得解.
【详解】因为 ,所以 ,
即 ,所以 .
故选:D.
2.C
求出 ,可得出 的值,利用导数的概念可求得所求极限的值.
【详解】因为 ,则 ,所以, ,所以, .
故选:C.
3.C
利用空间向量的线性运算求解.
【详解】 ,
.
故选:C
4.A
对函数求导并令 解不等式可得单调递减区间.
【详解】易知函数定义域为 ,
可得 ,显然 ,
令 ,可得 ,
因此函数 的单调递减区间是 .
故选:A
5.D
建立空间直角坐标系,求出 , ,利用线线角的向量法,即可求解.
【详解】如图,以 为坐标原点,建立空间直角坐标系,设正方体的边长为 ,
则 ,所以 , ,
设异面直线 与 所成的角为 ,
则 ,故选:D.
6.A
构造函数 ,利用导数研究 的单调性,得到 最大,再变形 ,利用 的单调性比较
的大小即可.
【详解】因为 ,设 ,则 ,
当 时, ,所以 在 上单调递增,
当 时, ,所以 在 上单调递减.
所以 在 时取到最大值,
所以 ,即 .
因为 , ,
又因为 ,所以 ,
因为 在 上单调递增,
所以 ,即 ,所以 .
故选:A
7.B
利用插空法求解即可.
【详解】先排男生共有 种方法,再排女生共有 种方法,由分步乘法计数原理可得满足条件的排法数为 ,
故选:B.
8.C
当 时,构造函数 ,求导结合已知得其单调性,进而可得当 时, ,当
时, ,结合奇函数的性质即可进一步得解.
【详解】当 时,令 ,则 ,所以 在 上单调递增,
当 时, ,即 ,
当 时, ,即 ,
因为函数 是定义在 上的奇函数,
所以 ,
当 时, ,当 时, ,
所以不等式 的解集为 .
故选:C.
9.BD
【详解】对于A,A与B关于平面 对称,则 ,故A错误;
对于B,由共面向量定理易知得B正确;
对于C,因为 ,故C错误;
对于D, ,因为A,B,C共线,所以 共线,
所以 ,所以 ,故D正确.
故选:BD.
10.ACD【详解】对于A、B,抽出的 件中恰好有 件是不合格品,则包括一件不合格品和两件合格品,共有
种抽取方法,故A正确B错误;
对于C、D,抽出的 件中至少有 件是不合格品,可以分为“有 件是不合格品”和“有2件是不合格
品”两种情况,“有 件是不合格品”有 种抽取方法,“有2件是不合格品”有 种抽取方法,
所以共有 种抽取方法. 故C正确.
另外,“至少有 件是不合格品”的对立事件是“3件都是合格品”,其抽取方法有 种,所以,抽出的
件中至少有 件是不合格品的抽取方法有 种.故D正确.
故选:ACD.
11.ACD
根据因式分解可得函数的零点,结合导函数的图像去研究函数的极大值、对称中心与单调性.
【详解】已知 ,所以 ,
当 时, ,方程有两个根,所以 正确,
当 时, 的解集为 , 的解集为 ,
所以 在 上单调减,在 上单调增,所以 在 处取极小值,所以 错误,
当 时, ,
所以 关于 中心对称,所以 正确,
当 时, 的解集为 ,而 ,所以 在 上
单调递增,所以 正确.
故选:
12. 或
由组合数的性质,代入计算,即可得到结果.【详解】由 可得 或 ,
解得 或 ,
又 ,解得 ,且 ,
所以 的值为 或 .
故答案为: 或
13.
利用导数判断单调性,即可求出极值点,进而求出函数的极值.
【详解】由 的定义域为 , ,
当 时, ,则 在 上单调递减;
当 时, ,则 在 上单调递增;
故 在 取得极小值为 ,无极大值;
故答案为: .
14.
取定空间的一个基底 ,表示出 ,再利用数量积的运算律求得答案.
【详解】在平行六面体 中, , ,
则 ,而 ,则 ,
而 ,则
,
所以 .
故答案为:15.(1) ;
(2) .
(1)求导即可代入求解,
(2)根据导数求解斜率,即可由点斜式求解.
【详解】(1)由 ,得 ,
又 ,
所以 ,解得 .
(2)由(1)知 , ,
∴ ,即切点为 ,
又 , ,
∴切线的斜率为 ,
故函数 的图象在点 处的切线方程为: ,
即 .
16.(1)120
(2)96
(3)32
(1)直接全排列即可得答案;
(2)注意首位不能为0,从不为0的四个数选一个放在首位,再从剩下的四个数选三个数全排列即可得答
案;
(3)分0在个位、 在个位、4在个位三种情况进行讨论,再由分类加法计数原理求解可得答案.【详解】(1)从5个数字任取4个进行全排列,故有 个;
(2)首位不能为0,则有 个;
(3)由题意,是偶数个位数必须是 .
分3种情况讨论:
①0在个位,十位必须比0大,千位数字不能是0且不能与个位和十位数字重复,百位数字在剩下的数字选
一个,所以共有 ;
② 在个位,十位数字必须比2大,千位数不能是0且不能与个位和十位数字重复,百位剩下2个里面选
一个.有 种选法;
③4在个位,里面没有比4大的数字,不存在这种可能.则共有 种情况.
17.(1)证明见解析
(2)
(1)分别以 , , 为 轴、 轴、 轴,建立空间直角坐标系,利用向量法证明即可;
(2)设平面 的一个法向量为 ,求出法向量,利用向量法求解解.
【详解】(1)如图,分别以 , , 为 轴、 轴、 轴,建立空间直角坐标系,
, ,
因为 在 上,故可设 ,又 ,
所以 ,解得 ,
所以 ,,
,即
, 平面 .
所以 平面 .
(2)设平面 的一个法向量为 ,
,
则 ,
,
令 ,得 ,所以得 ,
,
所以所求的距离为 ;
18.(1)答案见解析
(2)
(1)建立空间直角坐标系,利用两个半平面的法向量可得二面角的余弦值,进而得到正弦值;
(2)根据 为线段 上一点,设 ,,利用空间向量法求直线和平面所成角的正弦值
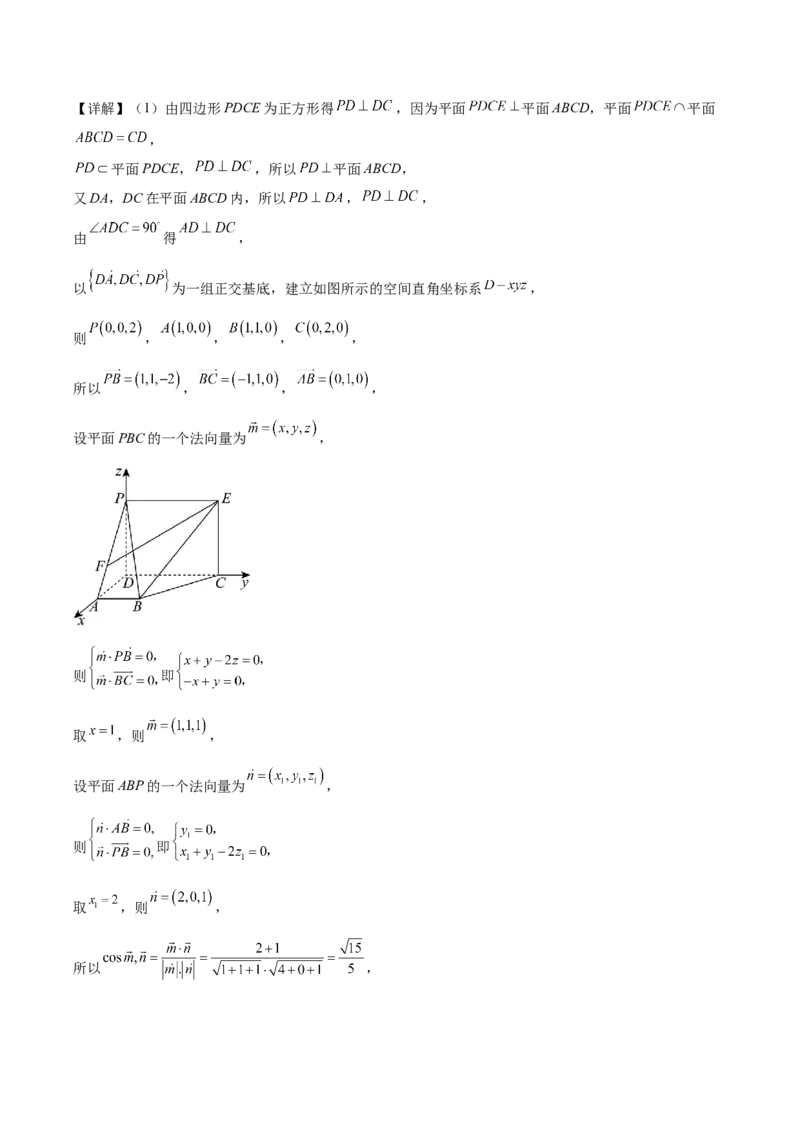
列式即可求解.【详解】(1)由四边形PDCE为正方形得 ,因为平面 平面ABCD,平面 平面
,
平面PDCE, ,所以 平面ABCD,
又DA,DC在平面ABCD内,所以 , ,
由 得 ,
以 为一组正交基底,建立如图所示的空间直角坐标系 ,
则 , , , ,
所以 , , ,
设平面PBC的一个法向量为 ,
则 即
取 ,则 ,
设平面ABP的一个法向量为 ,
则 即
取 ,则 ,
所以 ,所以二面角 的正弦值为 .
(2)设 , ,
则 ,
因为BQ与平面BCP所成角的正弦值为 ,
所以 ,
解得 或 ,因为 ,所以 ,
故
19.(1)
(2)
(3)证明见解析
(1)求得 ,得出函数 的单调区间,进而求得函数 最小值;
(2)根据题意,转化为 在 恒成立,令 ,求得 ,
得出函数 的单调性,求得 的最小值,即可得到答案.
令 ,解得 ,
(3)由函数 ,求得 ,令 ,求得 在上恒成立,得到函数 在 上单调递增,根据 是 的极值点,得到 ,结合
,即可证得 .
【详解】(1)解:由函数 ,可得其定义域为 ,且 ,
当 时, ;当 时, ,
所以 在 上单调递减,在 单调递增,
所以 .
(2)解:由 ,其中
可得 ,即 ,
由 对任意 恒成立,即 在 恒成立,
令 ,可得 ,
令 ,解得 ,
当 时, ;当 时, ,
所以函数 在 上单调递减,在 上单调递增,
所以 ,所以 ,即实数 的取值范围为 .
(3)解:由 ,可得 ,
令 ,可得 在 上恒成立,
所以函数 在 上单调递增,即函数 在 上单调递增,
因为 是 的极值点,所以存在 使得 ,即 ,又由 ,所以 ,
则 ,
所以 .