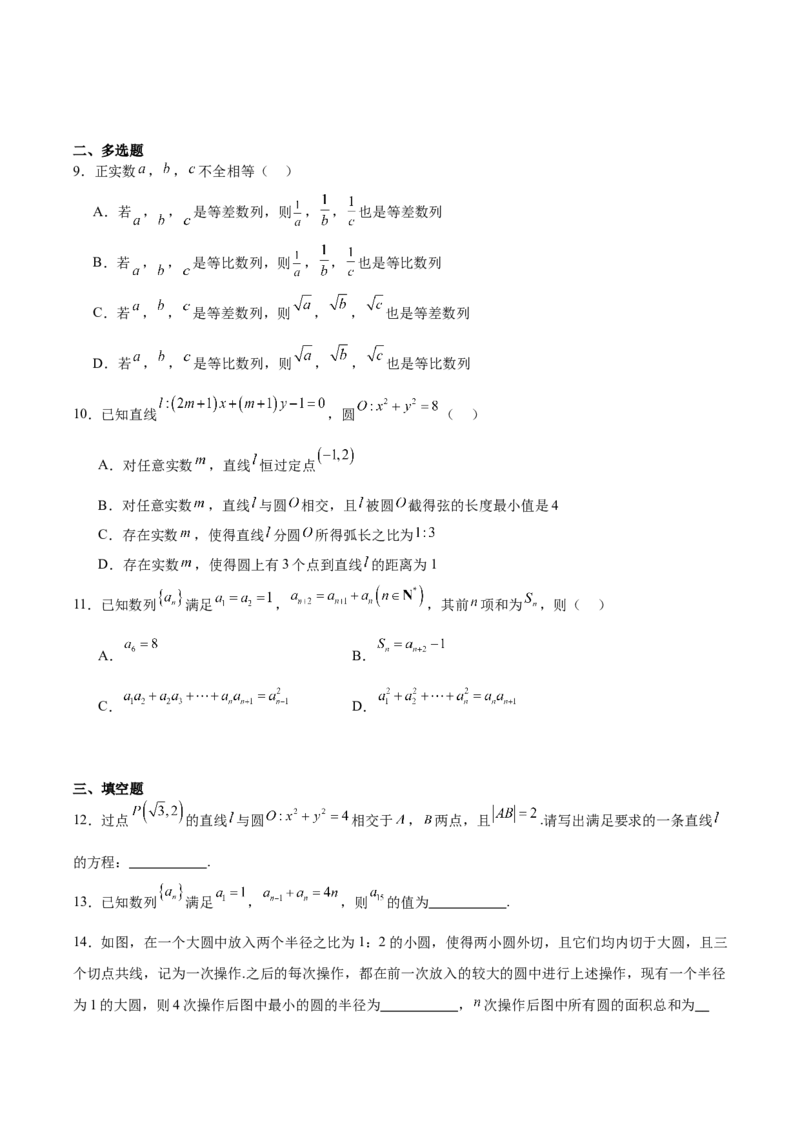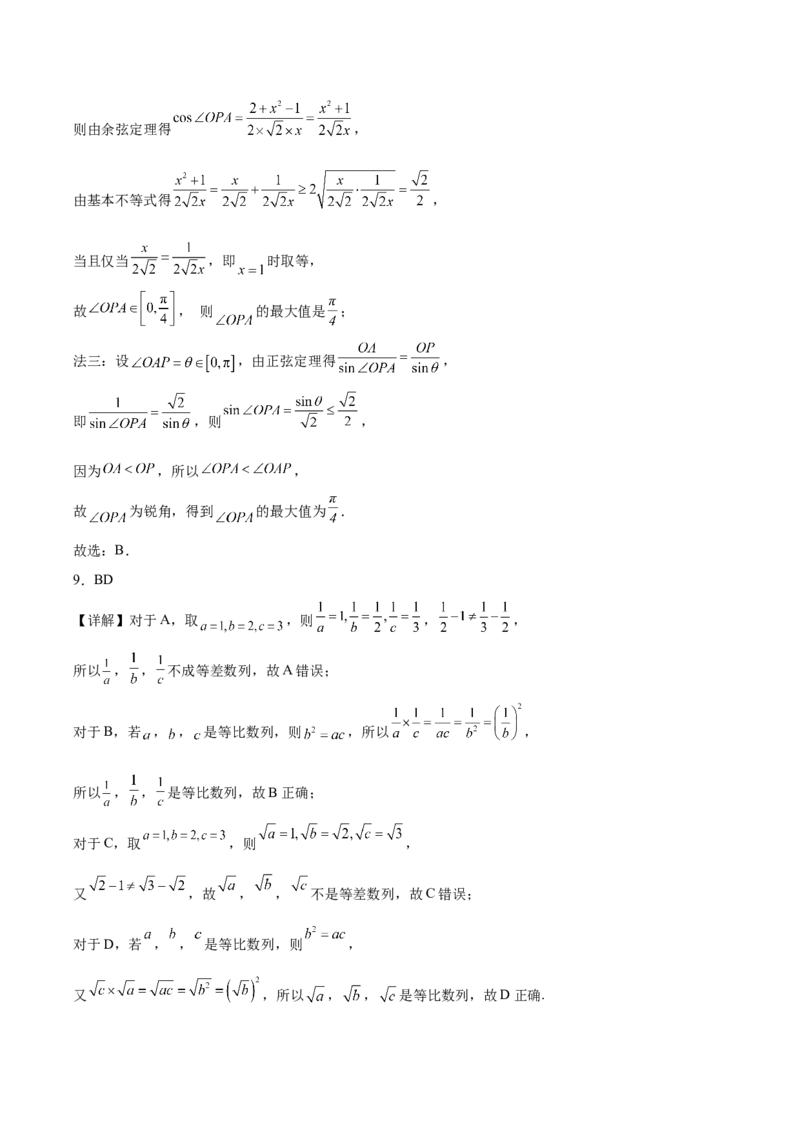文档内容
江苏省苏州市2025-2026学年高二上学期期中阳光调研
数学试卷
一、单选题
1.在等差数列 中,若 ,则 的值为( )
A.1 B.2 C.3 D.4
2.直线 过点 , ,则 的倾斜角为( )
A. B. C. D.
3.已知一个等差数列的项数为奇数,其中所有奇数项的和为290,所有偶数项的和为261.则此数列的项数
为( )
A.10 B.19 C.21 D.29
4.直线 与直线 及直线 相交于同一点,且 为 的一个方向向量,则 在 轴
上的截距为( )
A. B. C.1 D.2
5.已知数列 满足 ,则 的值为( )
A. B. C. D.2
6.已知点 , ,点 在 轴上, 是直角三角形,这样的三角形的个数是( )
A.1 B.2 C.3 D.4
7.已知等比数列 的首项为64,公比为 ,记 为数列 的前 项积,则当 时正整数 的最大
值为( )
A.12 B.13 C.14 D.15
8.已知点 是圆 上的动点,点 ,则 的最大值是( )
A. B. C. D.二、多选题
9.正实数 , , 不全相等( )
A.若 , , 是等差数列,则 , , 也是等差数列
B.若 , , 是等比数列,则 , , 也是等比数列
C.若 , , 是等差数列,则 , , 也是等差数列
D.若 , , 是等比数列,则 , , 也是等比数列
10.已知直线 ,圆 ( )
A.对任意实数 ,直线 恒过定点
B.对任意实数 ,直线 与圆 相交,且 被圆 截得弦的长度最小值是4
C.存在实数 ,使得直线 分圆 所得弧长之比为
D.存在实数 ,使得圆上有3个点到直线 的距离为1
11.已知数列 满足 , ,其前 项和为 ,则( )
A. B.
C. D.
三、填空题
12.过点 的直线 与圆 相交于 , 两点,且 .请写出满足要求的一条直线
的方程: .
13.已知数列 满足 , ,则 的值为 .
14.如图,在一个大圆中放入两个半径之比为1:2的小圆,使得两小圆外切,且它们均内切于大圆,且三
个切点共线,记为一次操作.之后的每次操作,都在前一次放入的较大的圆中进行上述操作,现有一个半径
为1的大圆,则4次操作后图中最小的圆的半径为 , 次操作后图中所有圆的面积总和为.
四、解答题
15.已知 的三个顶点分别是 , , .
(1)求 边上的中线所在直线的方程;
(2)求 的外接圆的方程.
16.已知圆 ,圆 .
(1)判断并证明圆 ,圆 的位置关系;
(2)若两圆 与 相交于 , 两点,满足 ,则称圆 与圆 正交.现有动圆 与圆 ,圆
均正交,自 引动圆 的切线.求证:切线长是定值.
17.记数列 的前 项和为 ,满足 .记数列 的前 项和为 ,满足 , ,
.
(1)求数列 , 的通项公式;
(2)求数列 的前 项和 .
18.已知数列 的第 项是由 个1构成的 位数,如: , , ,…数列 的第 项
是由1或2构成的所有 位数的和,如: , ,,…
(1)求数列 的通项公式及其前 项和 ;
(2)试求出 ,并直接写出数列 的一个通项公式(无需说明理由);
(3)求满足不等式 的正整数 的最小值.(参考数据: , )
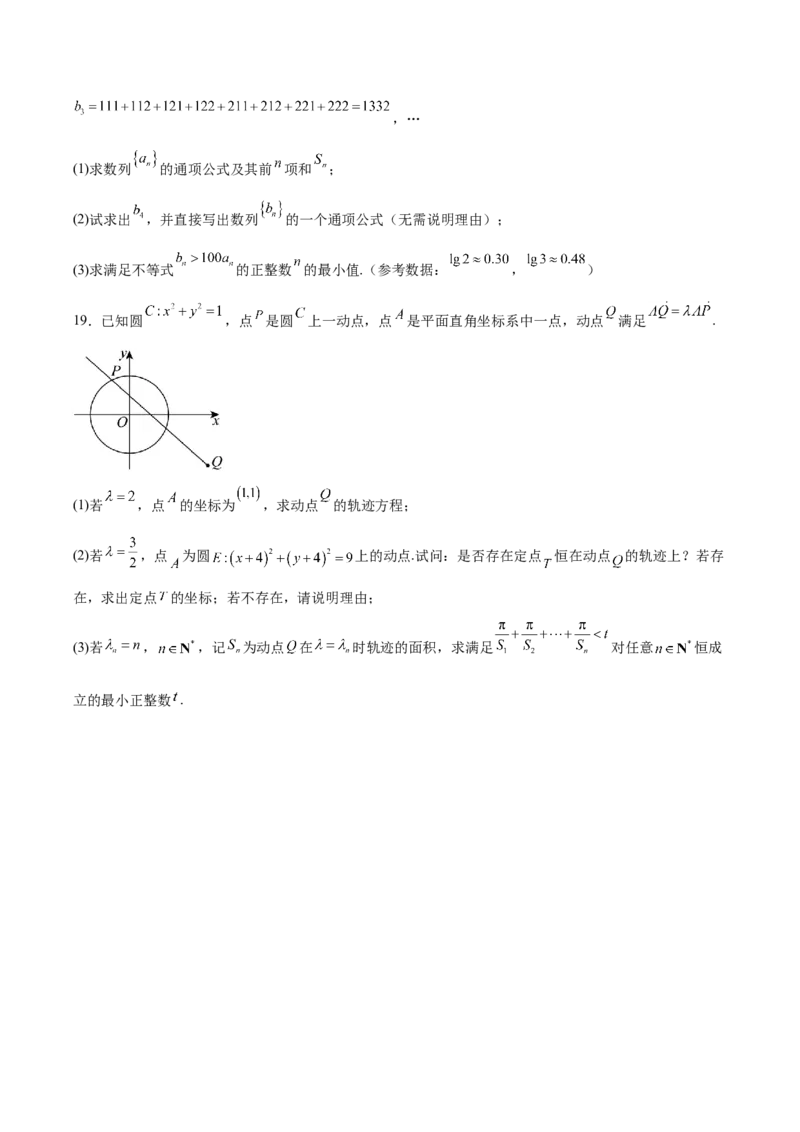
19.已知圆 ,点 是圆 上一动点,点 是平面直角坐标系中一点,动点 满足 .
(1)若 ,点 的坐标为 ,求动点 的轨迹方程;
(2)若 ,点 为圆 上的动点.试问:是否存在定点 恒在动点 的轨迹上?若存
在,求出定点 的坐标;若不存在,请说明理由;
(3)若 , ,记 为动点 在 时轨迹的面积,求满足 对任意 恒成
立的最小正整数 .参考答案
1.C
【详解】在等差数列中, .
故选:C.
2.D
【详解】因为直线 过点 , ,所以直线 的斜率 ,
设直线 的倾斜角 ,则 ,又 ,所以 ,
所以直线 的倾斜角为 .
故选:D.
3.B
【详解】设项数为 ,
则 ,
.
此数列共有19项.
故选:B
4.A
【详解】联立方程 ,直线 过点 ,
又 为直线的一个方向向量,则直线斜率为1,
直线 ,当 , ,即 在 轴上的截距为 .
故选:A
5.B
【详解】因为数列 满足 ,可得 , , ,…,
可得数列 是周期为3的周期数列,所以 .
故选:B.
6.C
【详解】设 .显然直线 斜率都存在.
若 为直角,则 ,所以 ,解得 ;
若 为直角,则 ,所以 ,解得 ;
若 为直角,则 ,所以 ,解得 .
故有三个满足要求的直角三角形.
故选:C
方法二:若 为直角,则 ,解得 ;
若 为直角,则 ,解得 ;
若 为直角,则 ,解得 .
故有三个满足要求的直角三角形.
故选:C
方法三:当 为直角顶点时,显然有两个这样的直角三角形;
若 为直角顶点, 中点 , ,则 ,而点 到 距离
为5, 此时有唯一点 ,符合要求.
故有三个满足要求的直角三角形.
故选:C
7.A【详解】由题意 , , ,
, , ,
当 时正整数 的最大值为12.
故选A.
8.B
【详解】法一:如图,设过 , , 三点的圆的半径为 ,
则 ,又 ,
所以 ,则 是锐角,可得 ,
故 取最大, 最大,
则 时, 取得最小值 ,此时 ,
而 是锐角,此时 ,
法二:如图,结合圆的性质设 ,则由余弦定理得 ,
由基本不等式得 ,
当且仅当 ,即 时取等,
故 , 则 的最大值是 ;
法三:设 ,由正弦定理得 ,
即 ,则 ,
因为 ,所以 ,
故 为锐角,得到 的最大值为 .
故选:B.
9.BD
【详解】对于A,取 ,则 , ,
所以 , , 不成等差数列,故A错误;
对于B,若 , , 是等比数列,则 ,所以 ,
所以 , , 是等比数列,故B正确;
对于C,取 ,则 ,
又 ,故 , , 不是等差数列,故C错误;
对于D,若 , , 是等比数列,则 ,
又 ,所以 , , 是等比数列,故D正确.故选:BD.
10.ACD
【详解】直线 即 ,
令 ,解得 ,
所以直线 过定点 ,故A正确;
,故定点 在圆 内, 直线 与圆 相交,
设 ,由圆的几何性质,当直线 与 垂直时,弦长最小,
,则最小弦长为 ,故B错误
对于C,若直线 分圆 所得弧长之比为1:3,则劣弧所对圆心角为 ,
此时弦长为 ,而 ,故这样的直线是存在的,
存在实数 满足条件,故C正确
对于D,圆 半径为 ,若圆上有3个点到直线 的距离为1,
则圆心到直线 距离为 , 圆心 到直线 的距离 ,
而 , 存在实数 满足条件,故D正确
故选:ACD.
11.ABD
【详解】 , , , , ,故A正确;
对于B,由 ,
,故B正确
对于C,当 时, ,而 , ,故C错误.因为 , ,
即 , ,…,
累加得
,故D正确.
故选:ABD.
12. 或 .(写出其中一个即可)
【详解】由题意知过点 的直线 与圆 相交于 , 两点,
当直线 的斜率不存在时,直线方程为 ,代入 中,
可得 ,即 坐标为 ,此时 ,符合题意;
当直线 的斜率存在时,设方程为 ,即 ,
设圆心O到直线l的距离为d,则 ,
由 ,圆的半径 可得 ,即 ,解得 ,
故 ,解得 ,
故直线l的方程为 ,即 ,
故答案为: 或 .(写出其中一个即可)
13.29
【详解】由 ,可得 ,两式相减 ,
是首项为1,公差为4的等差数列,.
故答案为: .
14.
【详解】 次操作后,小圆的半径依次为 ,
大圆的半径依次为 ,
所以小圆半径是首项为 ,公比为 等比数列,
大圆半径是首项为 ,公比为 等比数列,
4次操作后图中最小的圆的半径为 ;
次操作后,小圆面积和为:
,
大圆面积和为:
所以大圆与小圆面积和为 ,
则所有圆的面积总和为 .
故答案为:
15.(1)(2)
【详解】(1)线段 中点为 ,则 边中线的斜率为 ,
所以 边上的中线所在直线方程为 化简得 ,
(2)设 外接圆一般方程为 ,代入三点坐标得,
解得 ,
即 的外接圆方程为 ,
即 .
16.(1)两圆内含,证明见解析
(2)证明见解析
【详解】(1)两圆内含.
证明:因为圆 圆心 ,半径 ,圆 圆心 ,半径 ,
圆心距 ,所以两圆内含.
(2)证明:设动圆 圆心 ,半径为 ,动圆 与圆 交于 , 两点,由题意有 ,
所以 ,即 ,
动圆 与圆 交于 , 两点,同理可得 ,即 ,故 ,
则有 整理得 ,即圆心 ,所以半径 ,
自 引动圆 的切线,切线长 ,所以切线长是定值 .17.(1) ,
(2)
【详解】(1) ,当 时,
数列 是首项为2,公比为2的等比数列,
由 得 ,
整理得 ①, ②
②-①得 ,即
即数列 是等差数列, , , ,
(2)
,
,
两式相减 ,
即数列 的前 项和 .
18.(1) , ;(2) ,
(3)7
【详解】(1)依题意 ,
所以 ,又 ,
所以数列 为常数列, ,
,
;
(2)依题意 是由 个 位数相加,其个位上的数字和为 ,
十位上的数字和为 , ,第 位上的数字和为 ,
又 , , ,
所以 ,
,
所以 ,又 ,
所以 是以 为首项, 为公比的等比数列,所以 ,即 ;
(3)由 ,即 , ,
即 ,所以 ,
又 在定义域上单调递增,且 , ,
所以 的最小值为 .
19.(1)
(2)存在,
(3)2
【详解】(1) ,设 ,则
代入圆 得: ,即
即动点 的轨迹方程为: ;
(2) ,设 , ,则
, 分别在圆 和圆 上,则
整理可得 的轨迹方程为 .
显然恒过定点 ,故 ;
(3) 时, ,设 , ,则代入圆 得:
即 的轨迹方程为: ,则
,则 ,故
时, ,故