文档内容
绵阳南山中学实验学校高 2021 级高三(上)一诊模拟考试
理科数学
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上.
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改
动,用橡皮擦干净后,再选涂其它答案标号.回答非选择题时,将答案写在答题卡上,写在
本试卷上无效.
3.考试结束后,将答题卡交回.
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有
一项是符合题目要求的.
1. 设全集 ,集合 , ,则 ( )
A. B. C. D.
【答案】D
【解析】
【分析】先解一元二次不等式,化简集合A,再利用数轴进行集合的补集和交集运算可得.
【详解】解一元二次不等式化简集合A,得 ,
由 得 ,
所以 .
故选D.
【点睛】本题考查了一元二次不等式的解法,集合的交集和补集运算,用数轴运算补集和交集时,注意空心点
和实心点的问题,属基础题.
2. 若复数 ,则 ( )
A. B. C. D.
【答案】C
第1页/共30页
学科网(北京)股份有限公司【解析】
【分析】由复数的四则运算结合共轭复数的概念求解.
【详解】由 ,得 .
故选:C
3. 设 是等差数列 的前n项和,若 ,则 ( )
A. 15 B. 30 C. 45 D. 60
【答案】C
【解析】
【分析】根据等差数列的性质求出 ,再根据等差数列前n项和公式即可得解.
【详解】由题意得 ,所以 ,
所以 .
故选:C.
4. 已知命题 : ,使得 成立为真命题,则实数 的取值范围是( )
A. B. C. D.
【答案】B
【解析】
【分析】由一次函数和二次函数的图象和性质,知当 时,命题为真命题,当 时,需 ,最
后综合讨论结果,可得答案.
【详解】命题 为真命题等价于不等式 有解.
当 时,不等式变形为 ,则 ,符合题意;
当 时, ,解得 ;
当 时,总存在 ,使得 ;
第2页/共30页
学科网(北京)股份有限公司综上可得实数 的取值范围为 .
故选:B
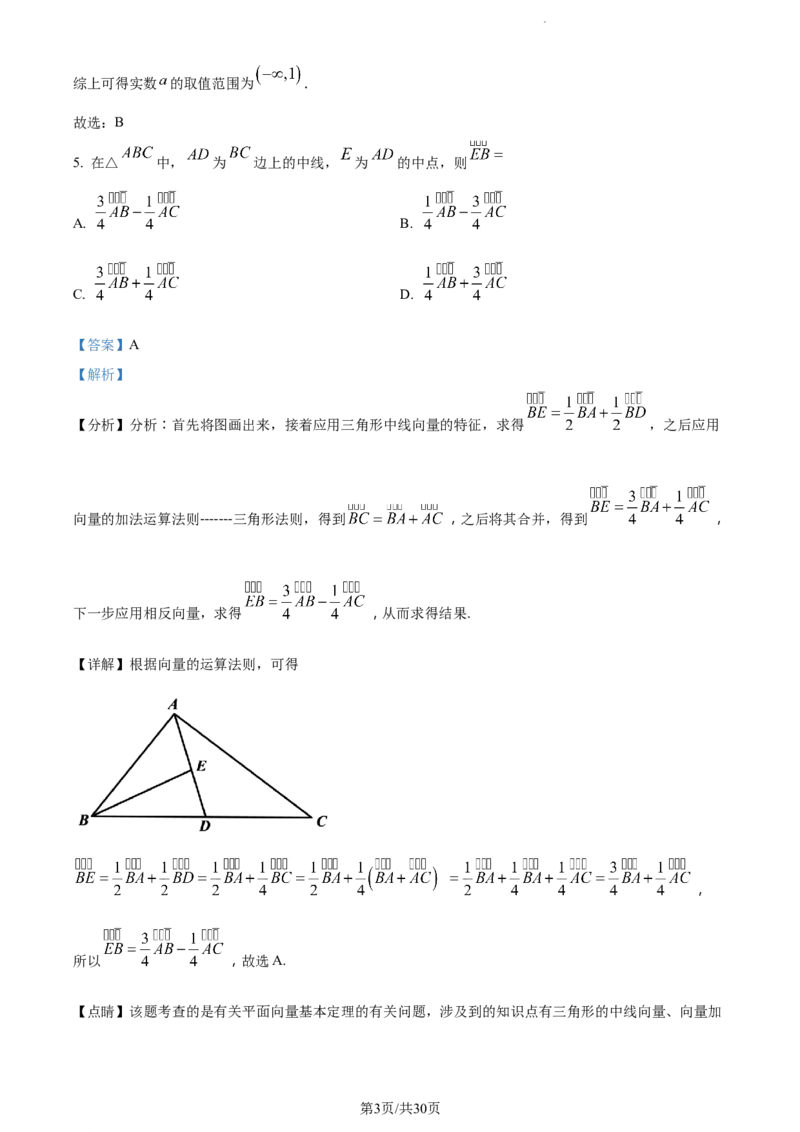
5. 在△ 中, 为 边上的中线, 为 的中点,则
A. B.
C. D.
【答案】A
【解析】
【分析】分析:首先将图画出来,接着应用三角形中线向量的特征,求得 ,之后应用
向量的加法运算法则-------三角形法则,得到 ,之后将其合并,得到 ,
下一步应用相反向量,求得 ,从而求得结果.
【详解】根据向量的运算法则,可得
,
所以 ,故选A.
【点睛】该题考查的是有关平面向量基本定理的有关问题,涉及到的知识点有三角形的中线向量、向量加
第3页/共30页
学科网(北京)股份有限公司法的三角形法则、共线向量的表示以及相反向量的问题,在解题的过程中,需要认真对待每一步运算.
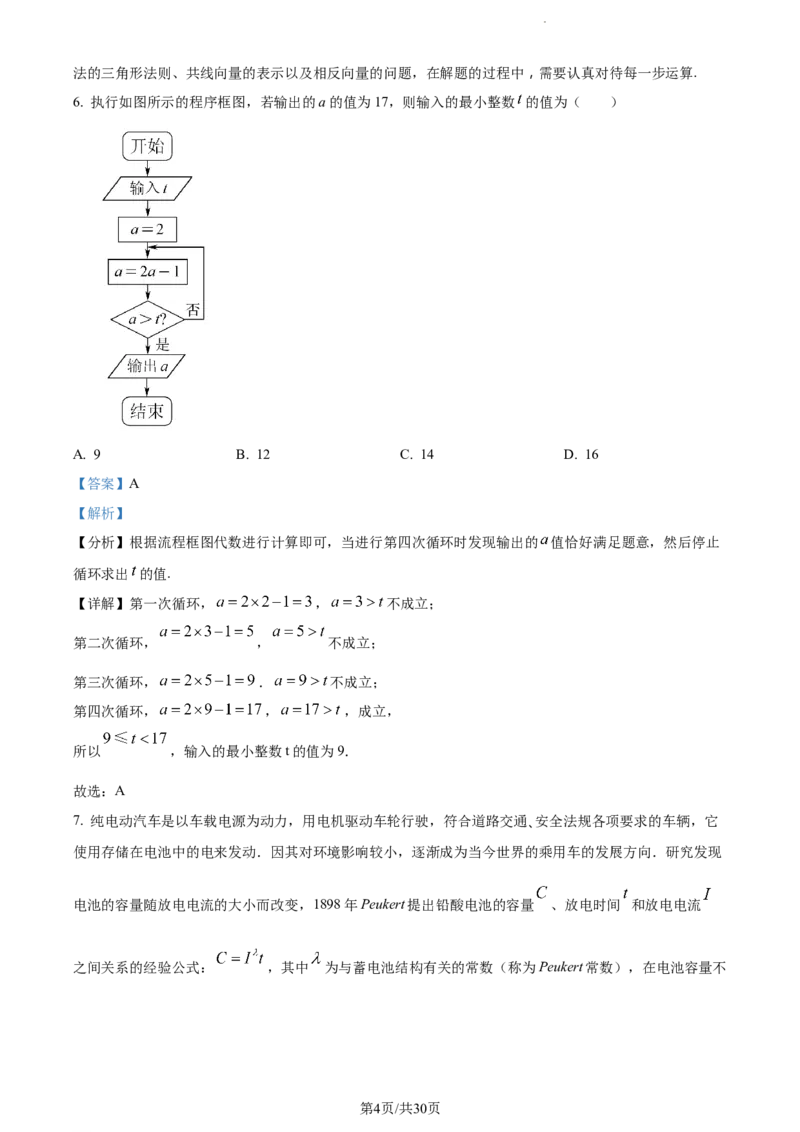
6. 执行如图所示的程序框图,若输出的a的值为17,则输入的最小整数 的值为( )
A. 9 B. 12 C. 14 D. 16
【答案】A
【解析】
【分析】根据流程框图代数进行计算即可,当进行第四次循环时发现输出的 值恰好满足题意,然后停止
循环求出 的值.
【详解】第一次循环, , 不成立;
第二次循环, , 不成立;
第三次循环, . 不成立;
第四次循环, , ,成立,
所以 ,输入的最小整数t的值为9.
故选:A
7. 纯电动汽车是以车载电源为动力,用电机驱动车轮行驶,符合道路交通、安全法规各项要求的车辆,它
使用存储在电池中的电来发动.因其对环境影响较小,逐渐成为当今世界的乘用车的发展方向.研究发现
电池的容量随放电电流的大小而改变,1898年Peukert提出铅酸电池的容量 、放电时间 和放电电流
之间关系的经验公式: ,其中 为与蓄电池结构有关的常数(称为Peukert常数),在电池容量不
第4页/共30页
学科网(北京)股份有限公司变的条件下,当放电电流为 时,放电时间为 ;当放电电流为 时,放电时间为 ,则该萻
电池的Peukert常数 约为( )(参考数据: , )
A. 1.12 B. 1.13 C. 1.14 D. 1.15
【答案】D
【解析】
【分析】根据题意可得 ,再结合对数式与指数式的互化及换底公式即可求解.
【详解】由题意知 ,
所以 ,两边取以10为底的对数,得 ,
所以 .
故选:D.
8. 若 ,则 ( )
A. B. C. D.
【答案】A
【解析】
【分析】由二倍角公式可得 ,再结合已知可求得 ,利用同角三
角函数的基本关系即可求解.
【详解】
,
第5页/共30页
学科网(北京)股份有限公司, , ,解得 ,
, .
故选:A.
【点睛】关键点睛:本题考查三角函数的化简问题,解题的关键是利用二倍角公式化简求出 .
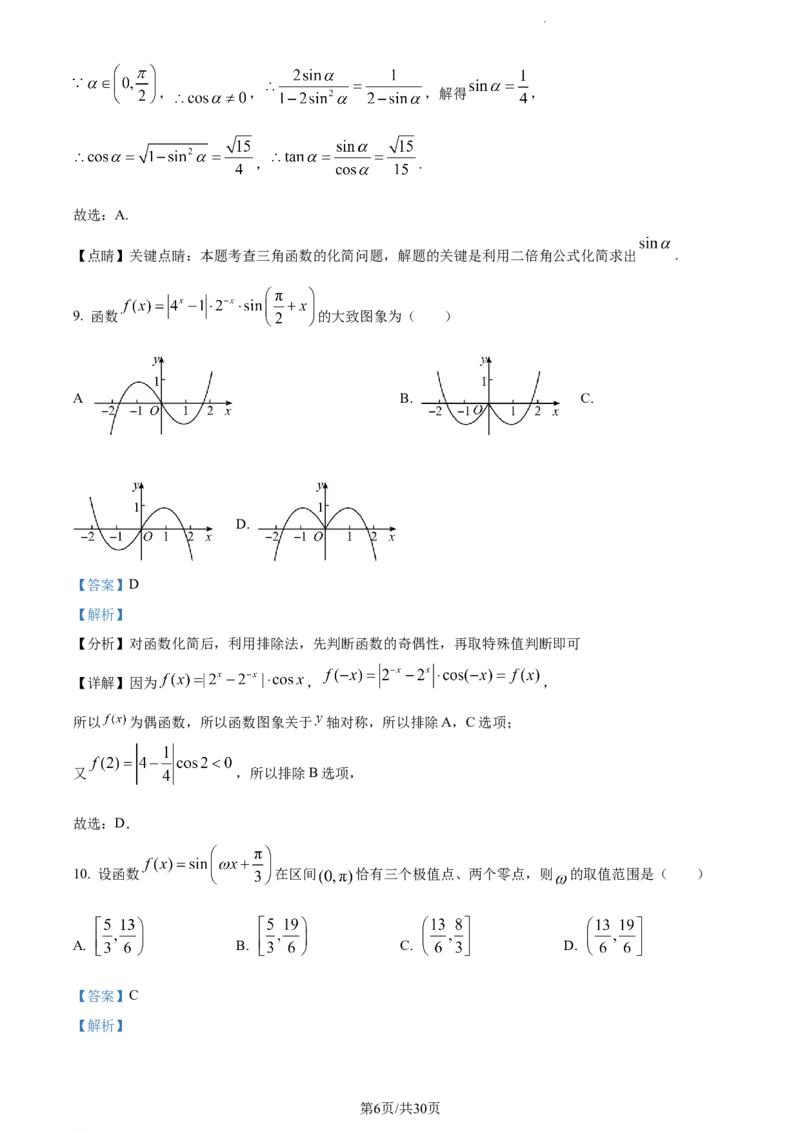
9. 函数 的大致图象为( )
A B. C.
.
D.
【答案】D
【解析】
【分析】对函数化简后,利用排除法,先判断函数的奇偶性,再取特殊值判断即可
【详解】因为 , ,
所以 为偶函数,所以函数图象关于 轴对称,所以排除A,C选项;
又 ,所以排除B选项,
故选:D.
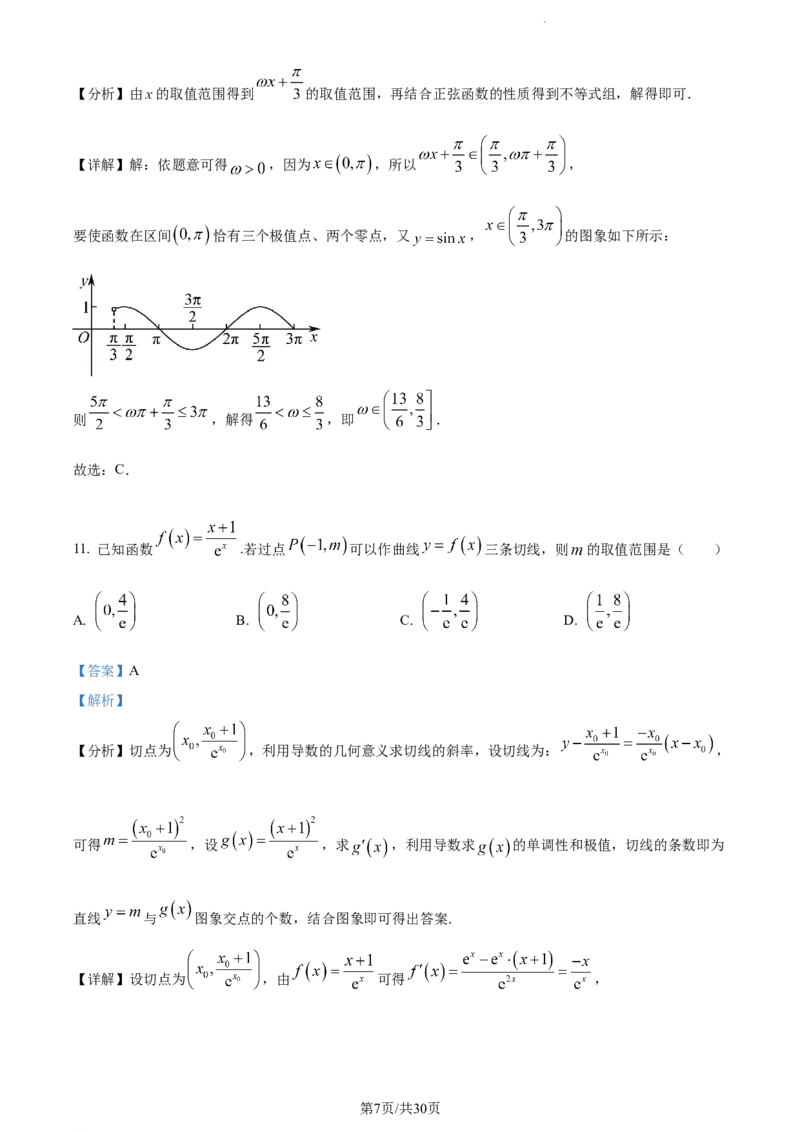
10. 设函数 在区间 恰有三个极值点、两个零点,则 的取值范围是( )
A. B. C. D.
【答案】C
【解析】
第6页/共30页
学科网(北京)股份有限公司【分析】由 的取值范围得到 的取值范围,再结合正弦函数的性质得到不等式组,解得即可.
【详解】解:依题意可得 ,因为 ,所以 ,
要使函数在区间 恰有三个极值点、两个零点,又 , 的图象如下所示:
则 ,解得 ,即 .
故选:C.
11. 已知函数 .若过点 可以作曲线 三条切线,则 的取值范围是( )
A. B. C. D.
【答案】A
【解析】
【分析】切点为 ,利用导数的几何意义求切线的斜率,设切线为: ,
可得 ,设 ,求 ,利用导数求 的单调性和极值,切线的条数即为
直线 与 图象交点的个数,结合图象即可得出答案.
【详解】设切点为 ,由 可得 ,
第7页/共30页
学科网(北京)股份有限公司所以在点 处的切线的斜率为 ,
所以在点 处的切线为: ,
因为切线过点 ,所以 ,
即 ,即这个方程有三个不等根即可,
切线的条数即为直线 与 图象交点的个数,
设 ,
则
由 可得 ,由 可得: 或 ,
所以 在 和 上单调递减,在 上单调递增,
当 趋近于正无穷, 趋近于0,当 趋近于负无穷, 趋近于正无穷,
的图象如下图,且 ,
要使 与 的图象有三个交点,则 .
则 的取值范围是: .
故选:A.
第8页/共30页
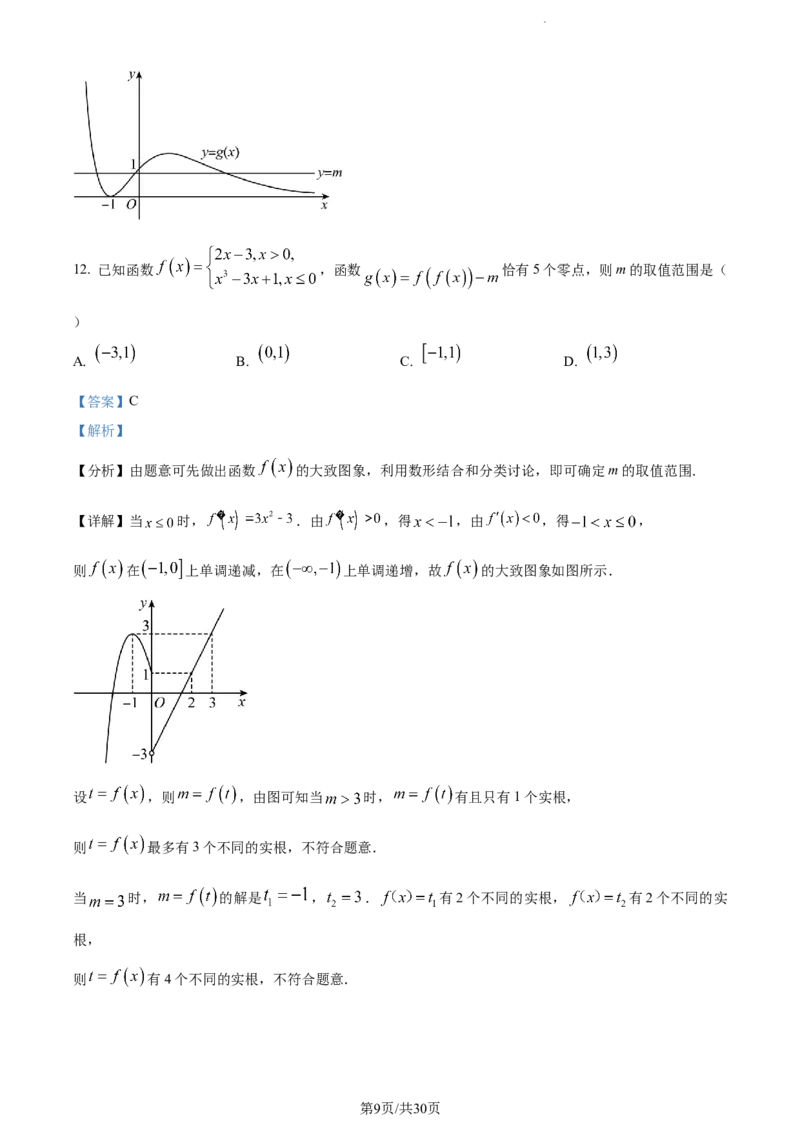
学科网(北京)股份有限公司12. 已知函数 ,函数 恰有5个零点,则m的取值范围是(
)
A. B. C. D.
【答案】C
【解析】
【分析】由题意可先做出函数 的大致图象,利用数形结合和分类讨论,即可确定m的取值范围.
【详解】当 时, .由 ,得 ,由 ,得 ,
则 在 上单调递减,在 上单调递增,故 的大致图象如图所示.
设 ,则 ,由图可知当 时, 有且只有1个实根,
则 最多有3个不同的实根,不符合题意.
当 时, 的解是 , . 有2个不同的实根, 有2个不同的实
根,
则 有4个不同的实根,不符合题意.
第9页/共30页
学科网(北京)股份有限公司当 时, 有3个不同的实根 , , ,且 , , .
有2个不同的实根, 有2个不同的实根, 有3个不同的实根,
则 有7个不同的实根,不符合题意.
当 时, 有2个不同的实根 , ,且 , .
有2个不同的实根, 有3个不同的实根,
则 有5个不同的实根,符合题意.
当 时, 有2个不同的实根 , ,且 , ,
有2个不同的实根, ,有2个不同的实根,则 有4个不同的实根,不符合题
意.
当 时, 有且只有1个实根,则 最多有3个不同的实根,不符合题意,
综上,m的取值范围是 .
故选:C.
【点睛】方法点睛:对于函数零点问题,若能够画图时可作出函数图像,利用数形结合与分类讨论思想,
即可求解.本题中,由图看出,m的讨论应有 , , , , 这几
种情况,也是解题关键.
二、填空题:本大题共4小题,每小题5分,共20分.
13. 已知向量 .若 ,则 ________.
【答案】 .
【解析】
【分析】利用向量的坐标运算法则求得向量 的坐标,利用向量的数量积为零求得 的值
【详解】 ,
第10页/共30页
学科网(北京)股份有限公司,解得 ,
故答案为: .
【点睛】本题考查平面向量的坐标运算,平面向量垂直的条件,属基础题,利用平面向量
垂直的充分必要条件是其数量积 .
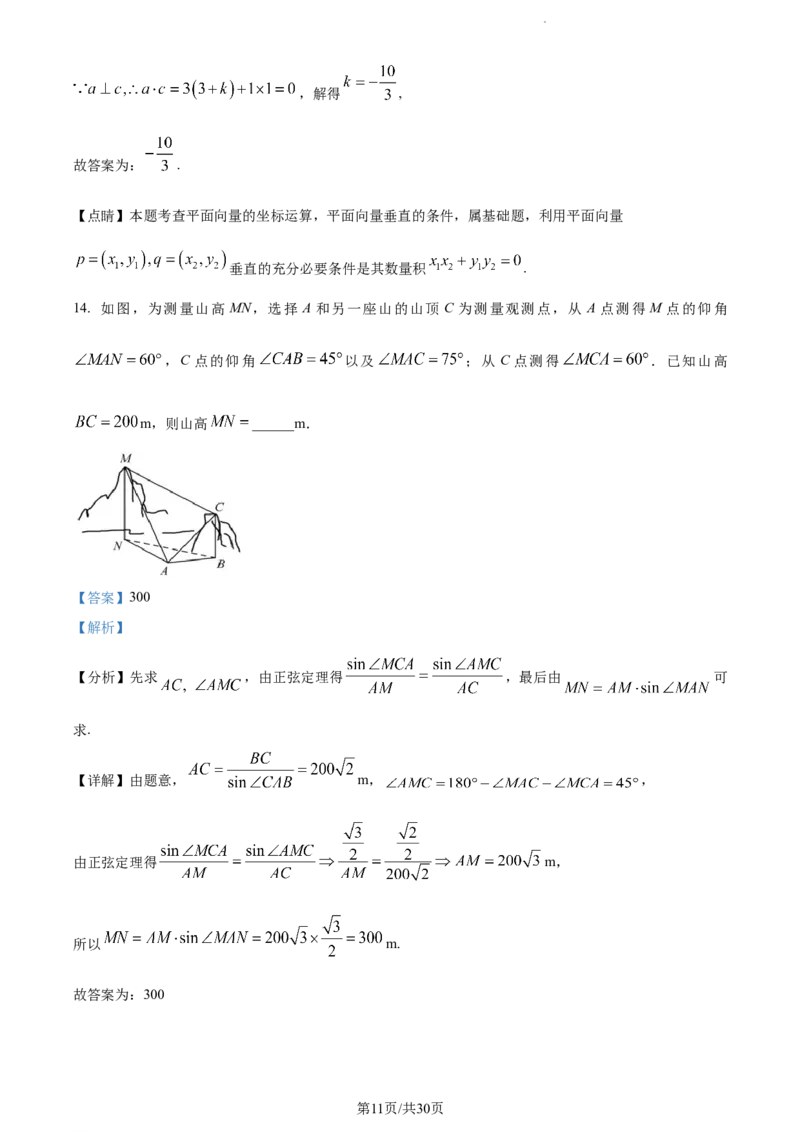
14. 如图,为测量山高 MN,选择 A 和另一座山的山顶 C 为测量观测点,从 A 点测得 M 点的仰角
,C 点的仰角 以及 ;从 C 点测得 .已知山高
m,则山高 ______m.
【答案】300
【解析】
【分析】先求 ,由正弦定理得 ,最后由 可
求.
【详解】由题意, m, ,
由正弦定理得 m,
所以 m.
故答案为:300
第11页/共30页
学科网(北京)股份有限公司15. 已知等比数列 的前3项和为 ,则 ___________.
【答案】3
【解析】
【分析】设等比数列 的公比为 ,根据已知条件利用等比数列的定义计算可得 , ,即
可求得 的值.
【详解】解:设等比数列 的公比为 , ,由题意 ,
因为前3项和为168,故 ,
又 ,
所以 , ,
则 .
故答案为:3.
16. 已知函数 是 的奇函数,对任意 ,都有 成立,当 ,
且 时,都有 ,有下列命题
① ②直线 是函数 图象的一条对称轴
③函数 在 上有5个零点 ④函数 在 上为减函数
则结论正确的有____________.
【答案】①②④
【解析】
【分析】根据题意,利用特殊值法求得 ,进而分析得到 时函数 的一条对称轴,,函
第12页/共30页
学科网(北京)股份有限公司数 时周期为4的周期函数,且函数 在 上单调递增,据此结合选项,逐项判定,即可求解.
【详解】由题意,函数 是 的奇函数,则 ,
对任意 ,都有 成立,
当 ,有 ,即 ,
则有 ,即 时函数 的一条对称轴,
又由 为奇函数,则 ,即 ,
可得 ,所以函数 时周期为4的周期函数,
当 ,且 时,都有 ,可函数 在 上单调递增,
对于①中,由 ,则 ,
所以
,所以①正确;
对于②中,由 时函数 的一条对称轴,且函数 时周期为4的周期函数,
则直线 是函数 图象的一条对称轴,所以②正确;
对于③中,函数 在 上有7个零点,分别为 ,所以C错误;
对于④中,函数 在 上为增函数且周期为4,可得 在 上为增函数,又由
是函数 图象的一条对称轴,则函数 在 上为减函数,所以④正确.
故答案为:①②④
三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,
每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.
(一)必考题:共60分.
第13页/共30页
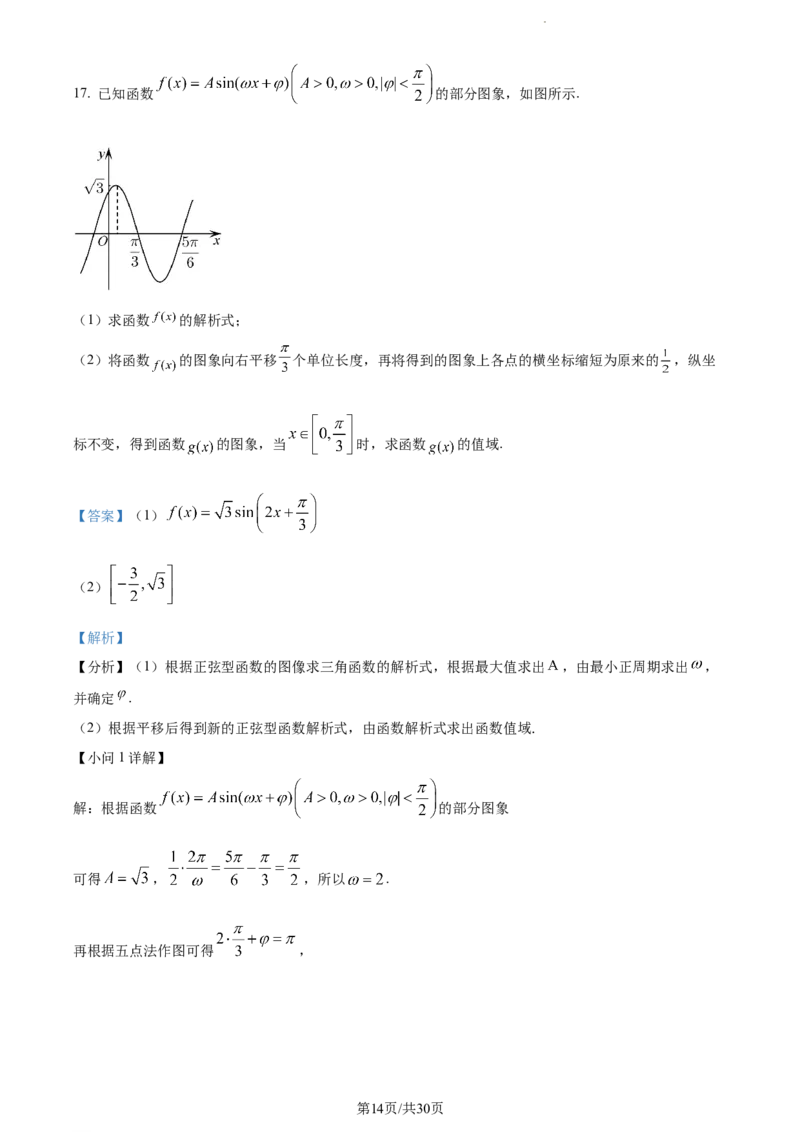
学科网(北京)股份有限公司17. 已知函数 的部分图象,如图所示.
(1)求函数 的解析式;
(2)将函数 的图象向右平移 个单位长度,再将得到的图象上各点的横坐标缩短为原来的 ,纵坐
标不变,得到函数 的图象,当 时,求函数 的值域.
【答案】(1)
(2)
【解析】
【分析】(1)根据正弦型函数的图像求三角函数的解析式,根据最大值求出 ,由最小正周期求出 ,
并确定 .
(2)根据平移后得到新的正弦型函数解析式,由函数解析式求出函数值域.
【小问1详解】
解:根据函数 的部分图象
可得 , ,所以 .
再根据五点法作图可得 ,
第14页/共30页
学科网(北京)股份有限公司所以 , .
【小问2详解】
将函数 的图象向右平移 个单位后,可得 的图象,
再将得到的图象上各点的横坐标缩短为原来的 ,纵坐标不变,得到函数 的图象.
由 ,可得
又 函数 在 上单调递增,在 单调递减
, ,
函数 在 的值域 .
18. 已知数列 的前n项和为 , ,且 . ,
.
(1)求数列 和 的通项公式;
的
(2)若 ,求数列 前n项和 .
【答案】(1) ,
(2)
【解析】
第15页/共30页
学科网(北京)股份有限公司【分析】(1)根据对数运算得 ,利用等比数列定义求通项公式,利用等差中项判断数列 为
等差数列,建立方程求出公差,从而可得 的通项;
(2)利用错位相减法计算即可.
【小问1详解】
∵ ,∴ ,则 ,所以 为等比数列,
又 ,得 ,所以 ,
由 知 是等差数列,且 , ,
∴ ,得 , .∴ .
【小问2详解】
因为 , ,所以 ,
所以
则
上面两式作差得
,
∴
19. 记 是内角 , , 的对边分别为 , , .已知 ,点 在边 上,
.
(1)证明: ;
第16页/共30页
学科网(北京)股份有限公司(2)若 ,求 .
【答案】(1)证明见解析;(2) .
【解析】
【分析】(1)根据正弦定理的边角关系有 ,结合已知即可证结论.
(2)方法一:两次应用余弦定理,求得边 与 的关系,然后利用余弦定理即可求得 的值.
【详解】(1)设 的外接圆半径为R,由正弦定理,
得 ,
因为 ,所以 ,即 .
又因为 ,所以 .
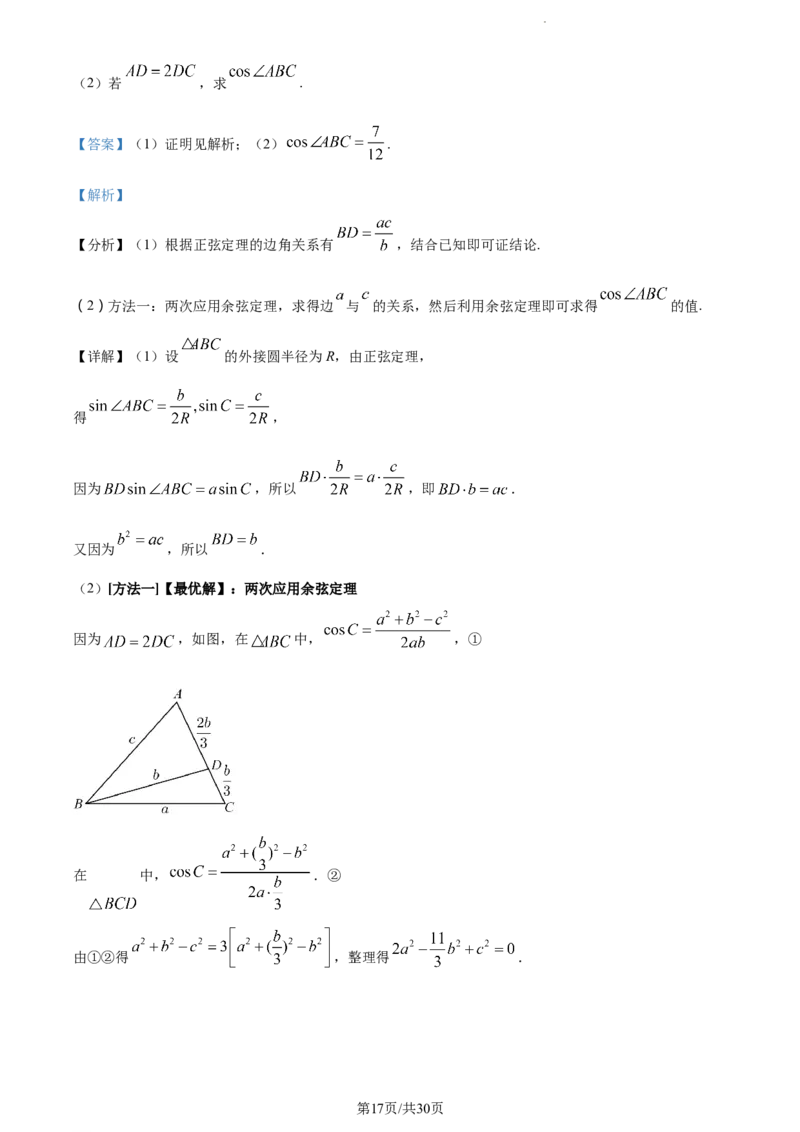
(2)[方法一]【最优解】:两次应用余弦定理
因为 ,如图,在 中, ,①
在 中, .②
由①②得 ,整理得 .
第17页/共30页
学科网(北京)股份有限公司又因为 ,所以 ,解得 或 ,
当 时, (舍去).
当 时, .
所以 .
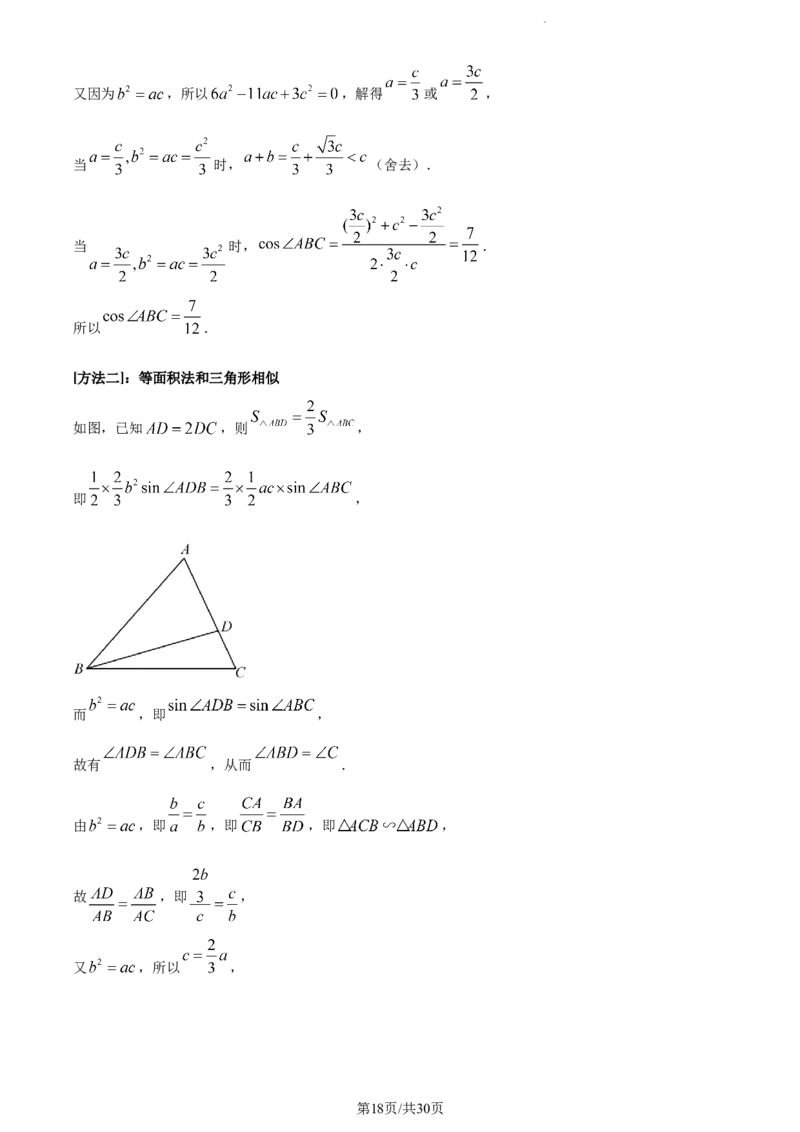
[方法二]:等面积法和三角形相似
如图,已知 ,则 ,
即 ,
而 ,即 ,
故有 ,从而 .
由 ,即 ,即 ,即 ,
故 ,即 ,
又 ,所以 ,
第18页/共30页
学科网(北京)股份有限公司则 .
[方法三]:正弦定理、余弦定理相结合
由(1)知 ,再由 得 .
在 中,由正弦定理得 .
又 ,所以 ,化简得 .
在 中,由正弦定理知 ,又由 ,所以 .
在 中,由余弦定理,得 .
故 .
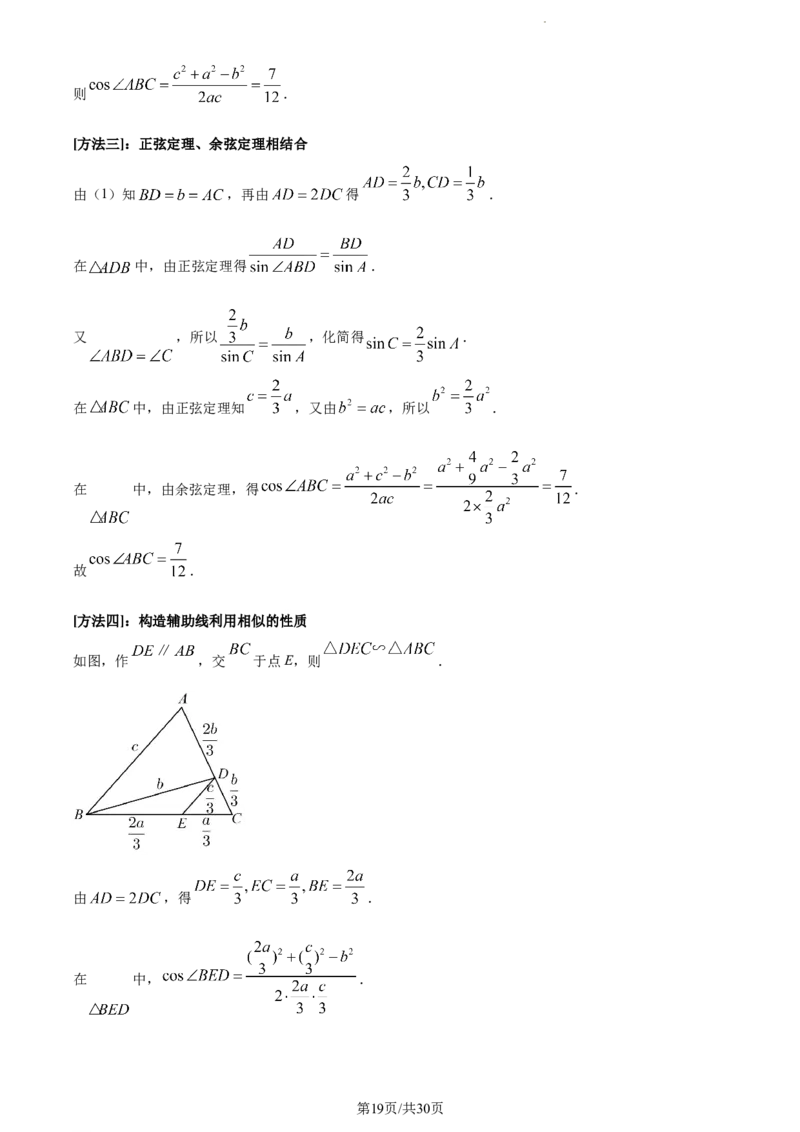
[方法四]:构造辅助线利用相似的性质
如图,作 ,交 于点E,则 .
由 ,得 .
在 中, .
第19页/共30页
学科网(北京)股份有限公司在 中 .
因为 ,
所以 ,
整理得 .
又因为 ,所以 ,
即 或 .
下同解法1.
[方法五]:平面向量基本定理
因为 ,所以 .
以向量 为基底,有 .
所以 ,
即 ,
又因为 ,所以 .③
由余弦定理得 ,
所以 ④
联立③④,得 .
所以 或 .
第20页/共30页
学科网(北京)股份有限公司下同解法1.
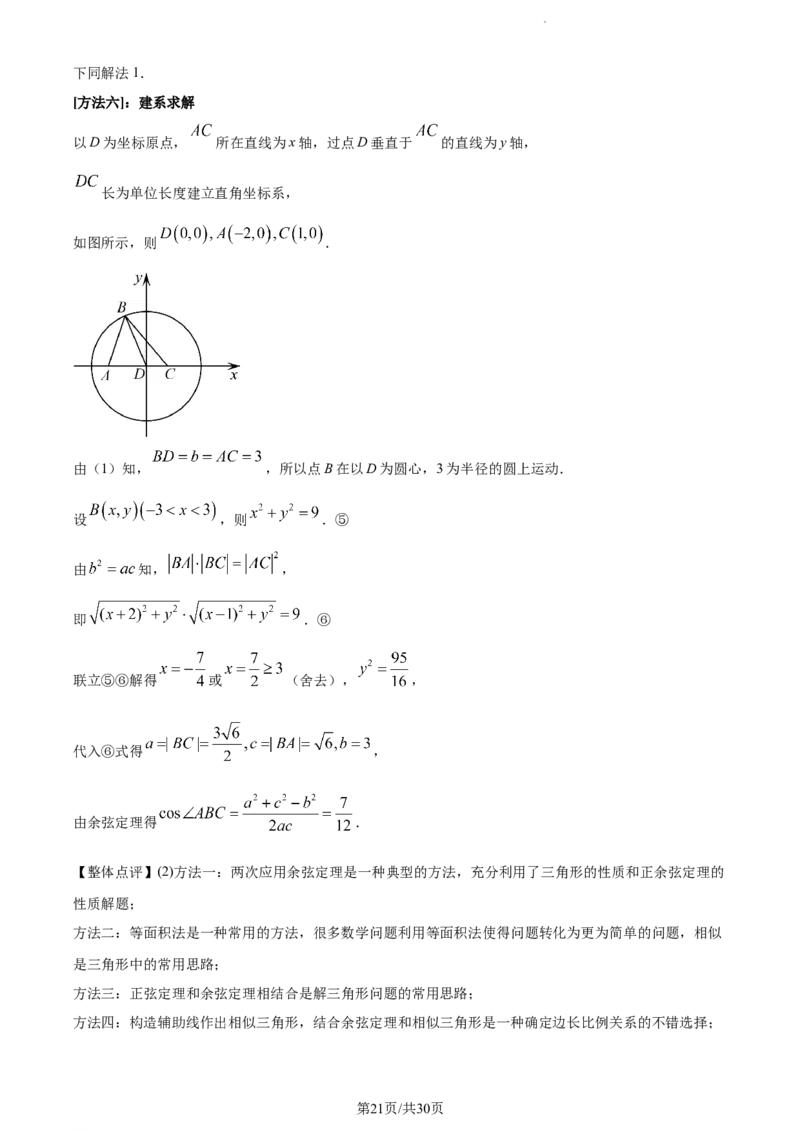
[方法六]:建系求解
以D为坐标原点, 所在直线为x轴,过点D垂直于 的直线为y轴,
长为单位长度建立直角坐标系,
如图所示,则 .
由(1)知, ,所以点B在以D为圆心,3为半径的圆上运动.
设 ,则 .⑤
由 知, ,
即 .⑥
联立⑤⑥解得 或 (舍去), ,
代入⑥式得 ,
由余弦定理得 .
【整体点评】(2)方法一:两次应用余弦定理是一种典型的方法,充分利用了三角形的性质和正余弦定理的
性质解题;
方法二:等面积法是一种常用的方法,很多数学问题利用等面积法使得问题转化为更为简单的问题,相似
是三角形中的常用思路;
方法三:正弦定理和余弦定理相结合是解三角形问题的常用思路;
方法四:构造辅助线作出相似三角形,结合余弦定理和相似三角形是一种确定边长比例关系的不错选择;
第21页/共30页
学科网(北京)股份有限公司方法五:平面向量是解决几何问题的一种重要方法,充分利用平面向量基本定理和向量的运算法则可以将
其与余弦定理充分结合到一起;
方法六:建立平面直角坐标系是解析几何的思路,利用此方法数形结合充分挖掘几何性质使得问题更加直
观化.
20. 已知函数 .
(1)讨论 的单调性;
(2)证明:当 时, .
【答案】(1)答案见解析
(2)证明见解析
【解析】
【分析】(1)先求导,再分类讨论 与 两种情况,结合导数与函数单调性的关系即可得解;
(2)方法一:结合(1)中结论,将问题转化为 的恒成立问题,构造函数
,利用导数证得 即可.
方法二:构造函数 ,证得 ,从而得到 ,进而将问题
转化为 的恒成立问题,由此得证.
【小问1详解】
因为 ,定义域为 ,所以 ,
当 时,由于 ,则 ,故 恒成立,
所以 在 上单调递减;
当 时,令 ,解得 ,
第22页/共30页
学科网(北京)股份有限公司当 时, ,则 在 上单调递减;
当 时, ,则 在 上单调递增;
综上:当 时, 在 上单调递减;
当 时, 在 上单调递减, 在 上单调递增.
【小问2详解】
方法一:
由(1)得, ,
要证 ,即证 ,即证 恒成立,
令 ,则 ,
令 ,则 ;令 ,则 ;
所以 在 上单调递减,在 上单调递增,
所以 ,则 恒成立,
所以当 时, 恒成立,证毕.
方法二:
令 ,则 ,
由于 在 上单调递增,所以 在 上单调递增,
又 ,
所以当 时, ;当 时, ;
第23页/共30页
学科网(北京)股份有限公司所以 在 上单调递减,在 上单调递增,
故 ,则 ,当且仅当 时,等号成立,
因为 ,
当且仅当 ,即 时,等号成立,
所以要证 ,即证 ,即证 ,
令 ,则 ,
令 ,则 ;令 ,则 ;
所以 在 上单调递减,在 上单调递增,
所以 ,则 恒成立,
所以当 时, 恒成立,证毕.
.
21 已知函数
(1)当 时,求曲线 在点 处的切线方程;
(2)若 在区间 各恰有一个零点,求a的取值范围.
【答案】(1)
(2)
【解析】
【分析】(1)先算出切点,再求导算出斜率即可
第24页/共30页
学科网(北京)股份有限公司,
(2)求导 对 分类讨论,对 分 两部分研究
【小问1详解】
的定义域为
当 时, ,所以切点为 ,所以切线斜
率为2
所以曲线 在点 处的切线方程为
【小问2详解】
设
若 ,当 ,即
所以 在 上单调递增,
故 在 上没有零点,不合题意
若 ,当 ,则
所以 在 上单调递增所以 ,即
所以 在 上单调递增,
故 在 上没有零点,不合题意
若
(1)当 ,则 ,所以 在 上单调递增
第25页/共30页
学科网(北京)股份有限公司所以存在 ,使得 ,即
当 单调递减
当 单调递增
所以
当 ,
令 则
所以 在 上单调递增,在 上单调递减,所以 ,
又 , ,
所以 在 上有唯一零点
又 没有零点,即 在 上有唯一零点
(2)当
设
所以 在 单调递增
所以存在 ,使得
当 单调递减
第26页/共30页
学科网(北京)股份有限公司当 单调递增,
又
所以存在 ,使得 ,即
当 单调递增,当 单调递减,
当 , ,
又 ,
而 ,所以当
所以 在 上有唯一零点, 上无零点
即 在 上有唯一零点
所以 ,符合题意
所以若 在区间 各恰有一个零点,求 的取值范围为
【点睛】
方法点睛:本题的关键是对 的范围进行合理分类,否定和肯定并用,否定只需要说明一边不满足即可,
肯定要两方面都说明.
(二)选考题:共10分.请考生在第22、23题中任选一题做答.如果多做,则按所做的第
一题记分.
选修4—4:坐标系与参考方程
第27页/共30页
学科网(北京)股份有限公司22. 在直角坐标系 中,曲线M的方程为 ,曲线N的方程为 ,以坐标原点O为极
点,x轴的正半轴为极轴,建立极坐标系.
(1)求曲线M,N的极坐标方程;
(2)若射线 与曲线M交于点A(异于极点),与曲线N交于点B,且
,求 .
【答案】(1) ;
(2)
【解析】
【分析】(1)根据极坐标与直角坐标的互化公式,即可求解曲线 和 的极坐标方程;
(2)将 代入曲线 和 的方程,求得 和 ,结合题意求
得 ,即可求解.
【小问1详解】
解:由 ,可得 ,即 ,
又由 ,可得 ,
所以曲线M的极坐标方程为 .
由 ,可得 ,即 ,
即曲线N的极坐标方程为 .
【小问2详解】
第28页/共30页
学科网(北京)股份有限公司解:将 代入 ,可得 ,
将 代入 ,可得 ,
则 ,
因为 ,所以 ,
又因为 ,所以 .
选修4—5:不等式选讲
23. 已知函数 .
(1)求不等式 的解集;
(2)设函数 的最小值为m,且正实数a,b,c满足 ,求证:
.
【答案】(1)
(2)证明见详解
【解析】
【分析】(1)分段讨论去绝对值即可求解;(2)利用绝对值不等式可求得 ,再利用基本不等式即
可证明.
【小问1详解】
由题意可得: ,
当 时,则 ,解得 ;
第29页/共30页
学科网(北京)股份有限公司当 时,则 ,解得 ;
当 时,则 ,解得 ;
综上所述:不等式 的解集为 .
【小问2详解】
∵ ,当且仅当 时等号成立,
∴函数 的最小值为 ,则 ,
又∵ ,当且仅当 ,即 时等号成立;
,当且仅当 ,即 时等号成立;
,当且仅当 ,即 时等号成立;
上式相加可得: ,当且仅当 时等号成立,
∴ .
第30页/共30页
学科网(北京)股份有限公司