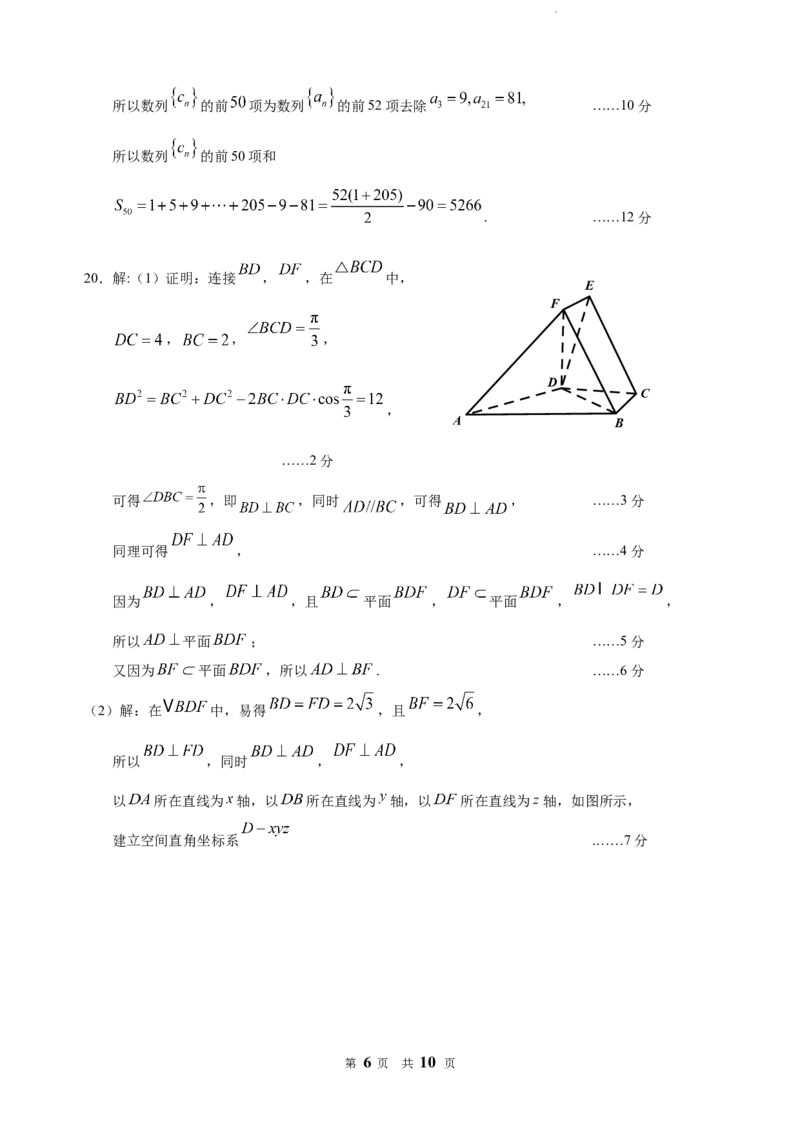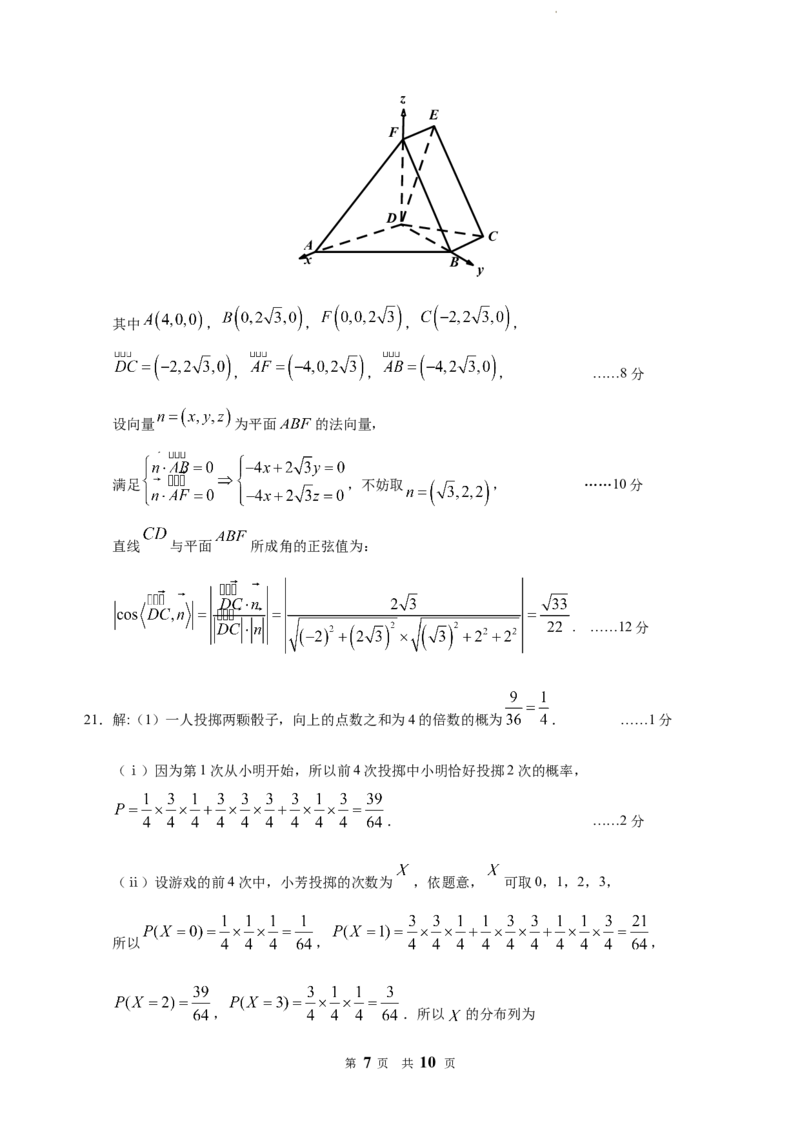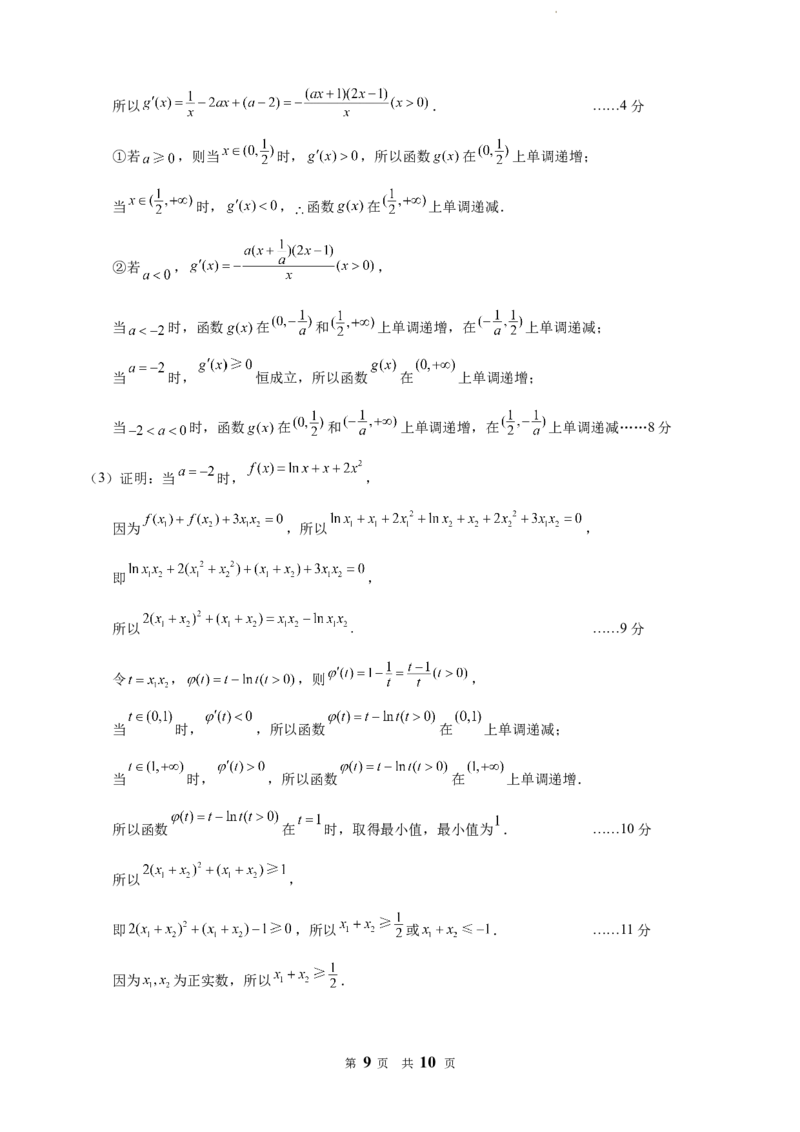文档内容
“宁化、永安、尤溪、大田、沙县一中”五校协作
2023—2024 学年高三 11 月联考
高三数学参考答案
一. 选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是
符合题目要求的.
1-4.CBCC 5-8.ADBD
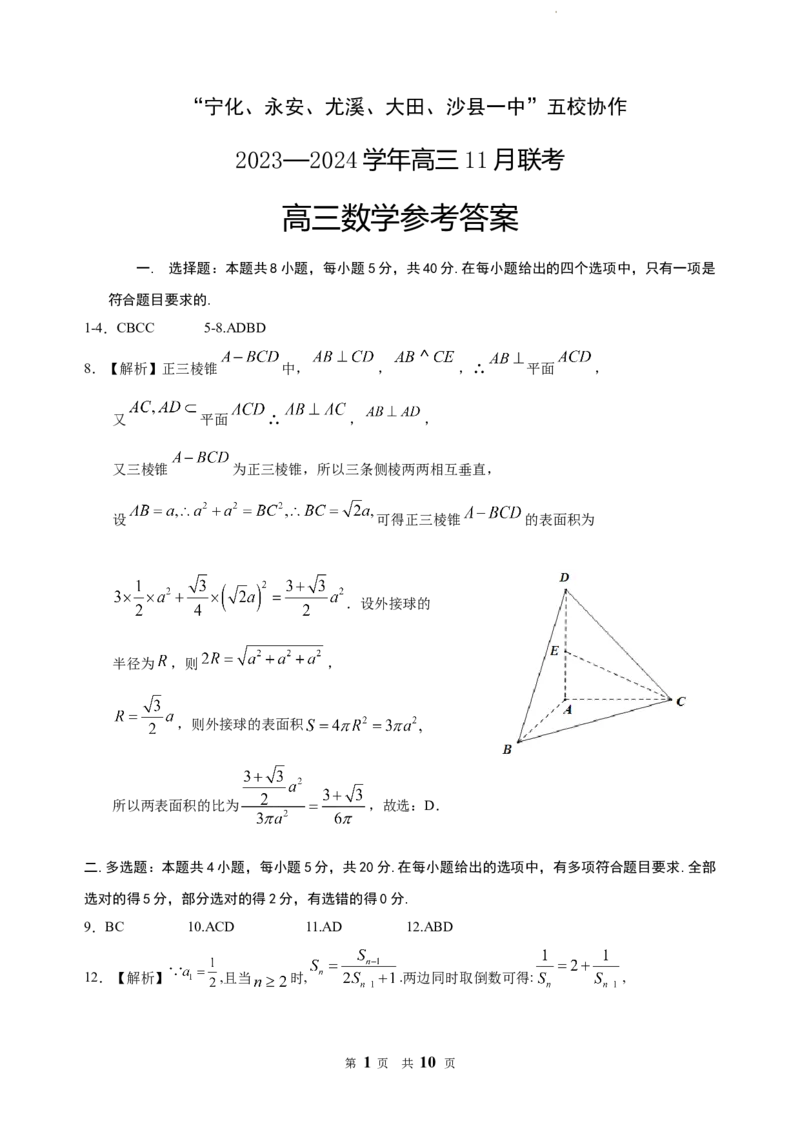
8.【解析】正三棱锥 中, , ,∴ 平面 ,
又 平面 ∴ , ,
又三棱锥 为正三棱锥,所以三条侧棱两两相互垂直,
设 可得正三棱锥 的表面积为
.设外接球的
半径为 ,则 ,
,则外接球的表面积
所以两表面积的比为 ,故选:D.
二.多选题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部
选对的得5分,部分选对的得2分,有选错的得0分.
9.BC 10.ACD 11.AD 12.ABD
12.【解析】 ,且当 时, .两边同时取倒数可得: ,
第 1 页 共 10 页
学科网(北京)股份有限公司即 ,且 , 数列 是等差数列,其公差为2,首项为2,所以A正确.
,可得 ,
当 时, ,所以 ;
所以 是先递减再递增的数列,当 时, ,所以 最大, 最小.B正确,C错
误..
对于D.当 时, ,又 时, ,对于上式也成立. ,
时, ,
,D正确
故选ABD
三.填空题:本题共4小题,每小题5分,共20分.
13.31 14.120 15. 16.
16.【解析】设函数 上的切点坐标为 ,且 ,函数 上的
切点坐标为 ,且 又 ,
则公切线的斜率 ,则 所以 ,
则公切线方程为 ,即
第 2 页 共 10 页
学科网(北京)股份有限公司代入 得: ,则 ,整理得
,
若总存在两条不同的直线与函数 图象均相切,则方程 有两个不同的实
根,设 ,则
令 得 ,当 时, 单调递增, 时,
单调递减,
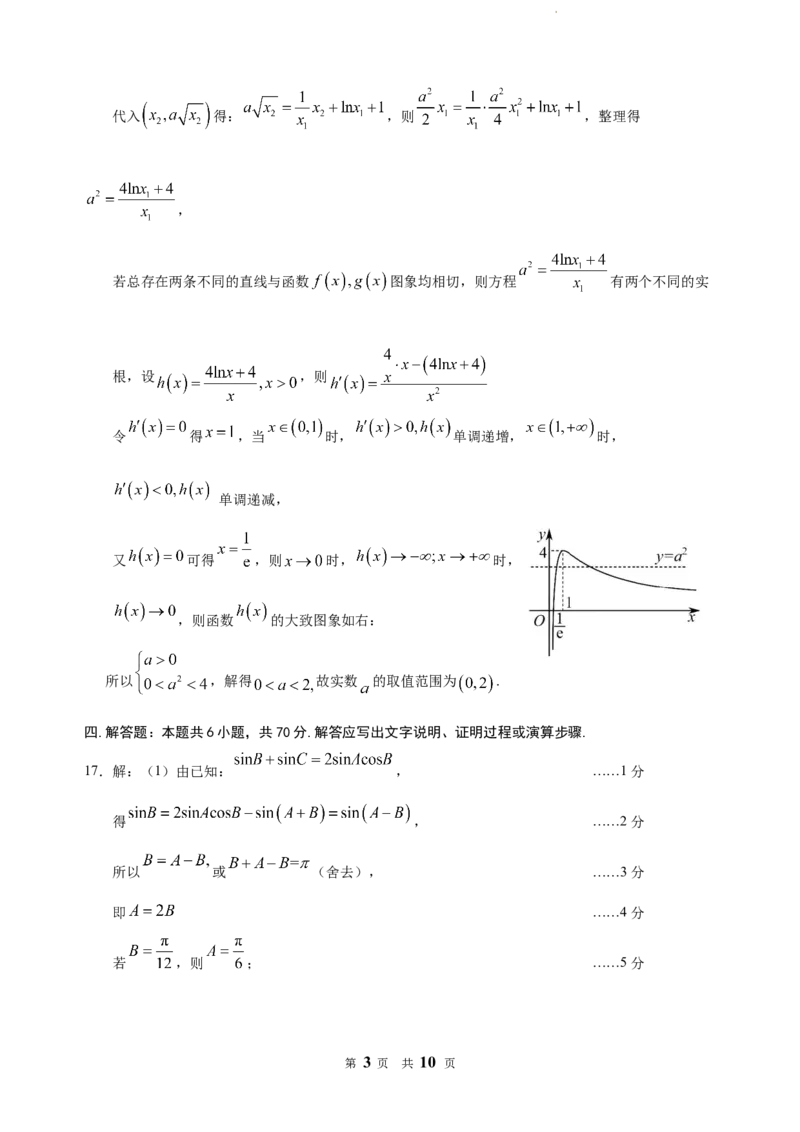
又 可得 ,则 时, 时,
,则函数 的大致图象如右:
所以 ,解得 故实数 的取值范围为 .
四.解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.解:(1)由已知: , ……1分
得 , ……2分
所以 或 (舍去), ……3分
即 ……4分
若 ,则 ; ……5分
第 3 页 共 10 页
学科网(北京)股份有限公司(2)由题意得
, ……7分
而 ,所以 , ……8分
故 ,即 . ……10分
18.解:(1)由题意可得 ,设函数 的最小正周期为 ,则 ,得
, ,此时, . ……2分
因为函数 的图象关于直线 对称,则 ,
, , , ,则 ……4分
令 ,得
,∴取 , ……6分
因此,函数 在区间 上的递增区间为 . ……7分
(2)又因为 ,所以函数 图象的对称中心为 ,…8分
则 ,所以 , ……10分
第 4 页 共 10 页
学科网(北京)股份有限公司解得 , ……11分
当 时, 取到了最小正值为 . ……12分
19 . 解 : ( 1 ) 设 等 差 数 列 的 公 差 为 , 则 等 差 数 列 通 项 公 式 为
,
所以 ,
所以 ,所以 ,所以 , ……3分
又因为 ,所以当 时, ,
两式相减可得 ,即 ,
令 ,则 ,解得 ,
所以数列 是以3为首项,3为公比的等比数列,所以 . ……6分
法二、由 可得 , ,
所以 ,解得 ,(其他同上)
法三、由 可得
解得 ,(其他同上)
(2)由(1)可知,
第 5 页 共 10 页
学科网(北京)股份有限公司所以数列 的前 项为数列 的前52项去除 ……10分
所以数列 的前50项和
. ……12分
20.解:(1)证明:连接 , ,在 中,
E
F
, , ,
D
C
,
A B
……2分
可得 ,即 ,同时 ,可得 , ……3分
同理可得 , ……4分
因为 , ,且 平面 , 平面 , ,
所以 平面 ; ……5分
又因为 平面 ,所以 . ……6分
(2)解:在 中,易得 ,且 ,
所以 ,同时 , ,
以 所在直线为 轴,以 所在直线为 轴,以 所在直线为 轴,如图所示,
建立空间直角坐标系 .……7分
第 6 页 共 10 页
学科网(北京)股份有限公司z
E
F
D
C
A
x B
y
其中 , , , ,
, , , ……8分
设向量 为平面 的法向量,
满足 ,不妨取 , ……10分
直线 与平面 所成角的正弦值为:
. ……12分
21.解:(1)一人投掷两颗骰子,向上的点数之和为4的倍数的概为 . ……1分
(ⅰ)因为第1次从小明开始,所以前4次投掷中小明恰好投掷2次的概率,
. ……2分
(ⅱ)设游戏的前4次中,小芳投掷的次数为 ,依题意, 可取0,1,2,3,
所以 , ,
, .所以 的分布列为
第 7 页 共 10 页
学科网(北京)股份有限公司0 1 2 3
…5分
所以 . ……6分
(2)若第1次从小芳开始,则第 次由小芳投掷骰子有两种情况:
①第 次由小芳投掷,第 次继续由小芳投掷,其概率为 ;
②第 次由小明投掷,第 次由小芳投掷,其概率为
. ……8分
因为①②两种情形是互斥的,所以
, ……10分
所以 .
因为 ,所以 是以 为首项, ……11分
为公比的等比数列,所以 ,即 . ……12分
22.(1)解:因为 ,所以 , ……1分
因为 在 处取得极值,所以 ,解得 . ……2分
验证:当 时, ,
易得 在 处取得极大值. ……3分
(2)解:因为 ,
第 8 页 共 10 页
学科网(北京)股份有限公司所以 . ……4分
①若 ,则当 时, ,所以函数 在 上单调递增;
当 时, , 函数 在 上单调递减.
②若 , ,
当 时,函数 在 和 上单调递增,在 上单调递减;
当 时, 恒成立,所以函数 在 上单调递增;
当 时,函数 在 和 上单调递增,在 上单调递减……8分
(3)证明:当 时, ,
因为 ,所以 ,
即 ,
所以 . ……9分
令 , ,则 ,
当 时, ,所以函数 在 上单调递减;
当 时, ,所以函数 在 上单调递增.
所以函数 在 时,取得最小值,最小值为 . ……10分
所以 ,
即 ,所以 或 . ……11分
因为 为正实数,所以 .
第 9 页 共 10 页
学科网(北京)股份有限公司当 时, ,此时不存在 满足条件,
所以 . ……12分
第 10 页 共 10 页
学科网(北京)股份有限公司