文档内容
数学试卷
注意事项:
1.答题前,考生务必用黑色碳素笔将自己的姓名、准考证号、考场号、座位号在答题卡上填写
清楚.
2.每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦
干净后,再选涂其他答案标号.在试题卷上作答无效.
3.考试结束后,请将本试卷和答题卡一并交回.满分150分,考试用时120分钟.
一、单项选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有
一项是符合题目要求的)
1.已知集合 , ,则集合 的元素个数为( )
A.2 B.3 C.4 D.5
2.复数 (其中 为虚数单位)的虚部为( )
A.2 B.1 C. D.
3.已知向量 , ,若 ,则 ( )
A. B.1
C. D.
4.为了树立和践行绿水青山就是金山银山的理念, 市某高中全体教师于2023年3月12日开展植树活动,
购买柳树、银杏、梧桐、樟树四种树苗共计1200棵,比例如图所示.青年教师、中年教师、老年教师报名参
加植树活动的人数之比为 ,若每种树苗均按各年龄段报名人数的比例进行分配,则中年教师应分得梧
桐的数量为( )
A.60棵 B.100棵 C.144棵 D.160棵
5.设随机变量 服从正态分布 ,若 ,则 的值为( )
A.9 B.7 C.5 D.4
6.纯电动汽车是以车载电源为动力,用电机驱动车轮行驶,符合道路交通、安全法规各项要求的车辆,它使
用存储在电池中的电来发动.因其对环境影响较小,逐渐成为当今世界的乘用车的发展方向.研究发现电池
学科网(北京)股份有限公司的容量随放电电流的大小而改变,1898年Peukert提出铅酸电池的容量 、放电时间 和放电电流 之间关系
的经验公式: ,其中 为与蓄电池结构有关的常数(称为Peukert常数),在电池容量不变的条件下,
当放电电流为 时,放电时间为 ;当放电电流为 时,放电时间为 ,则该蓄电池的Peukert
常数 约为(参考数据: , )( )
A.1.12 B.1.13
C.1.14 D.1.15
7.某圆锥的轴截面是一个边长为8的等边三角形,在该圆锥中内接一个圆柱,则该圆柱的侧面积的最大值为
( )
A. B.
C. D.
8.已知定义域为 的函数 ,其导函数为 ,且满足 , ,则( )
A. B.
C. D.
二、多项选择题(本大题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多
个选项是符合题目要求的,全部选对的得5分,选对但不全的得2分,有选错的得0分)
9.已知数列 的前 项和为 ,且满足 , ,则下列说法正确的
是( )
A.数列 为递增数列
B.数列 的前 项和为
C.数列 的通项公式为
D.数列 不是递增数列
10.有6个相同的球,分别标有数字1,2,3,4,5,6,从中不放回地随机取两次,每次取1个球,甲表示
事件“第一次取出的球的数字是奇数”,乙表示事件“第二次取出的球的数字是偶数”,丙表示事件“两次
学科网(北京)股份有限公司取出的球的数字之和是奇数”,丁表示事件“两次取出的球的数字之和是偶数”,则( )
A.乙发生的概率为 B.丙发生的概率为
C.甲与丁相互独立 D.丙与丁互为对立事件
11.已知函数 满足: , ,则( )
A.函数 的值域为
B.函数 的图象关于直线 对称
C.函数 是奇函数
D.函数 在 上单调递减
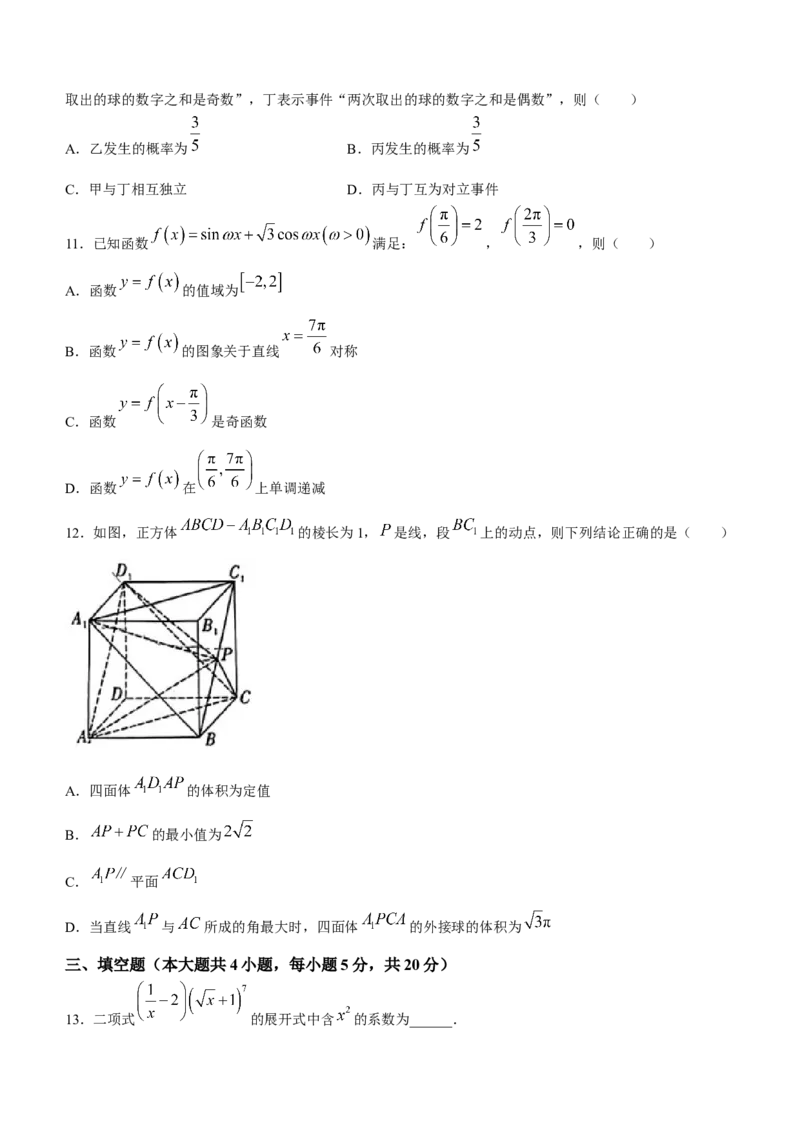
12.如图,正方体 的棱长为1, 是线,段 上的动点,则下列结论正确的是( )
A.四面体 的体积为定值
B. 的最小值为
C. 平面
D.当直线 与 所成的角最大时,四面体 的外接球的体积为
三、填空题(本大题共4小题,每小题5分,共20分)
13.二项式 的展开式中含 的系数为______.
学科网(北京)股份有限公司14.核桃(又称胡桃、羌桃)、扁桃、腰果、榛子并称为世界著名的“四大干果”.它的种植面积很广,但
因地域不一样,种植出来的核桃品质也有所不同:现已知甲、乙两地盛产核桃,甲地种植的核桃空壳率为
2%(空壳率指坚果,谷物等的结实性指标,因花未受精,壳中完全无内容,称为空壳),乙地种植的核桃空
壳率为4%,将两地种植出来的核桃混放在一起,已知甲地和乙地核桃数分别占总数的60%,40%,从中任取
一个核桃,则该核桃是空壳的概率是______.
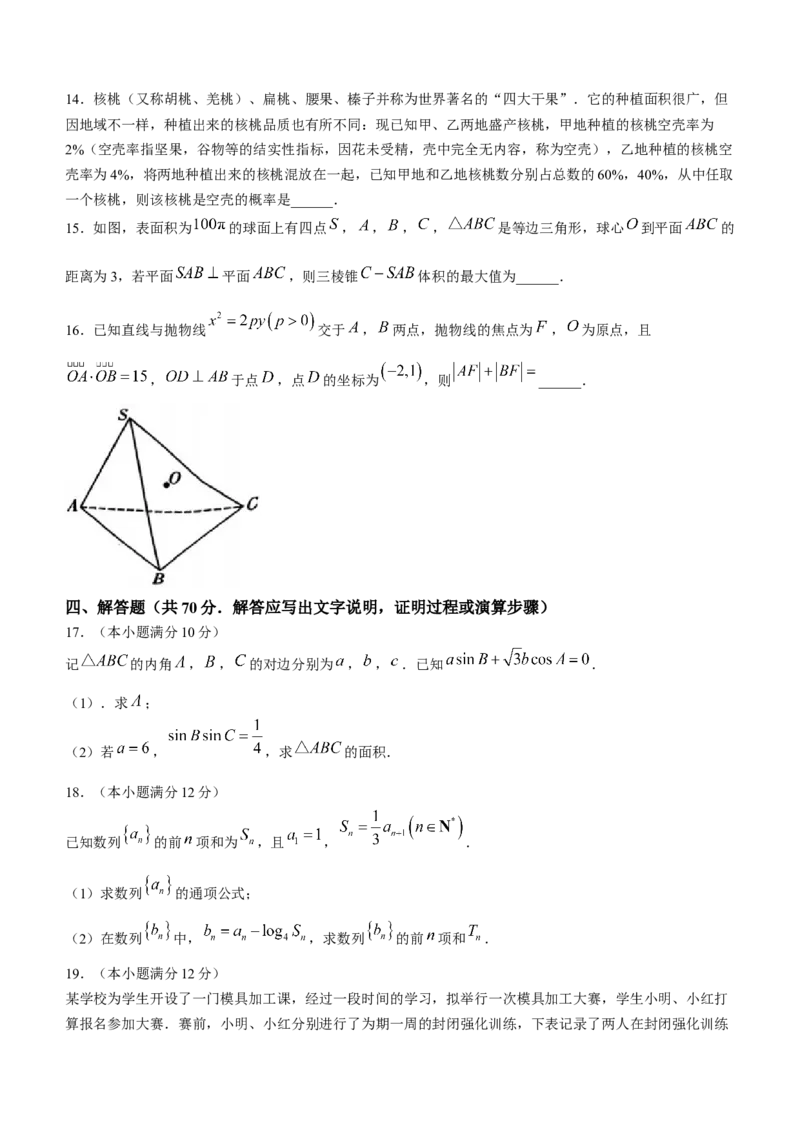
15.如图,表面积为 的球面上有四点 , , , , 是等边三角形,球心 到平面 的
距离为3,若平面 平面 ,则三棱锥 体积的最大值为______.
16.已知直线与抛物线 交于 , 两点,抛物线的焦点为 , 为原点,且
, 于点 ,点 的坐标为 ,则 ______.
四、解答题(共70分.解答应写出文字说明,证明过程或演算步骤)
17.(本小题满分10分)
记 的内角 , , 的对边分别为 , , .已知 .
(1).求 ;
(2)若 , ,求 的面积.
18.(本小题满分12分)
已知数列 的前 项和为 ,且 , .
(1)求数列 的通项公式;
(2)在数列 中, ,求数列 的前 项和 .
19.(本小题满分12分)
某学校为学生开设了一门模具加工课,经过一段时间的学习,拟举行一次模具加工大赛,学生小明、小红打
算报名参加大赛.赛前,小明、小红分别进行了为期一周的封闭强化训练,下表记录了两人在封闭强化训练
学科网(北京)股份有限公司期间每天加工模具成功的次数,其中小明第7天的成功次数 忘了记录,但知道 , ( ,
分别表示小明、小红第 天的成功次数).
第一天 第二天 第三天 第四天 第五天 第六天 第七天
序号 1 2 3 4 5 6 7
16 20 20 25 30 36
小明成功次数
16 22 25 26 32 35 35
小红成功次数
(1)求这7天内小明成功的总次数不少于小红成功的总次数的概率;
(2)根据小明这7天内前6天的成功次数,求其成功次数 关于序号 的线性回归方程,并估计小明第七天
成功次数 的值.
参考公式:回归方程 中斜率与截距的最小二乘估计公式分别为:
, .
参考数据: ; .
20.(本小题满分12分)
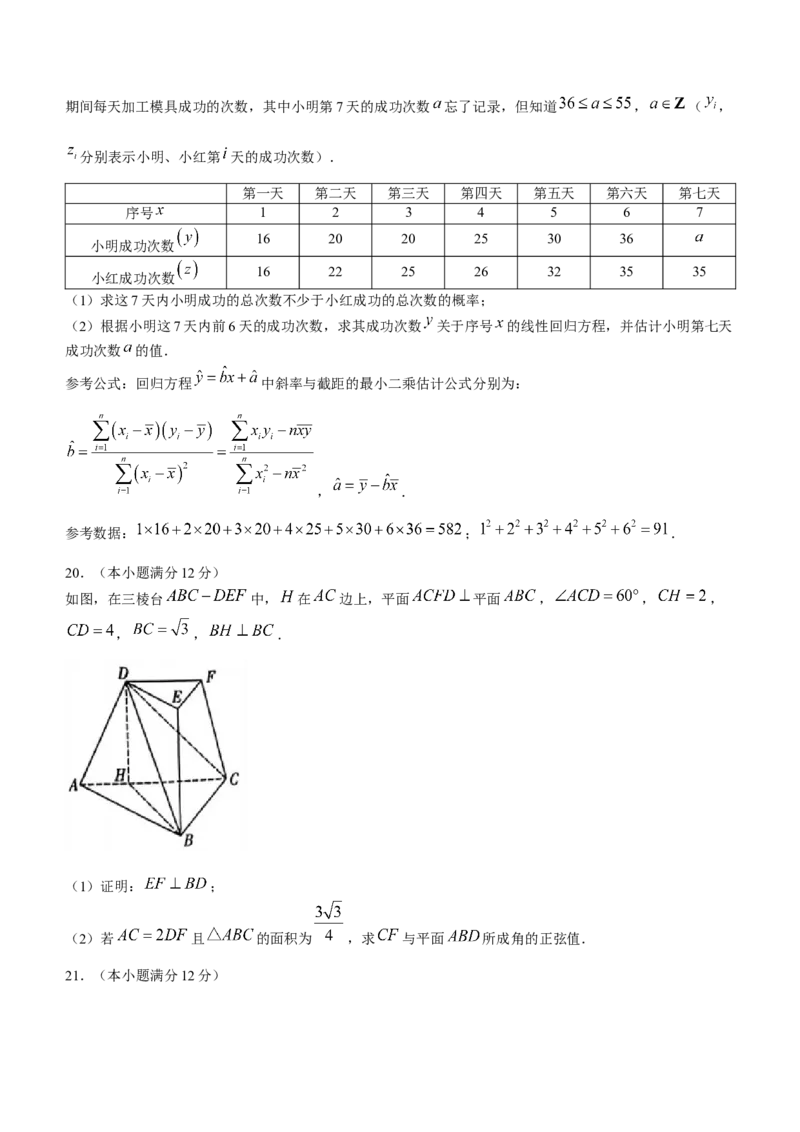
如图,在三棱台 中, 在 边上,平面 平面 , , ,
, , .
(1)证明: ;
(2)若 且 的面积为 ,求 与平面 所成角的正弦值.
21.(本小题满分12分)
学科网(北京)股份有限公司已知椭圆 的上、下顶点分别是 , ,点 (异于 , 两点)在椭圆 上,
直线 与 的斜率之积为 ,椭圆 的短轴长为4.
(1)求 的标准方程;
(2)已知 ,直线 与椭圆 的另一个交点为 ,且直线 与 相交于点 ,证明:点 在定
直线上.
22.(本小题满分12分)
已知函数 , .
(1)若 ,讨论函数 的单调性;
(2)当 时, 恒成立,求 的取值范围.
学科网(北京)股份有限公司