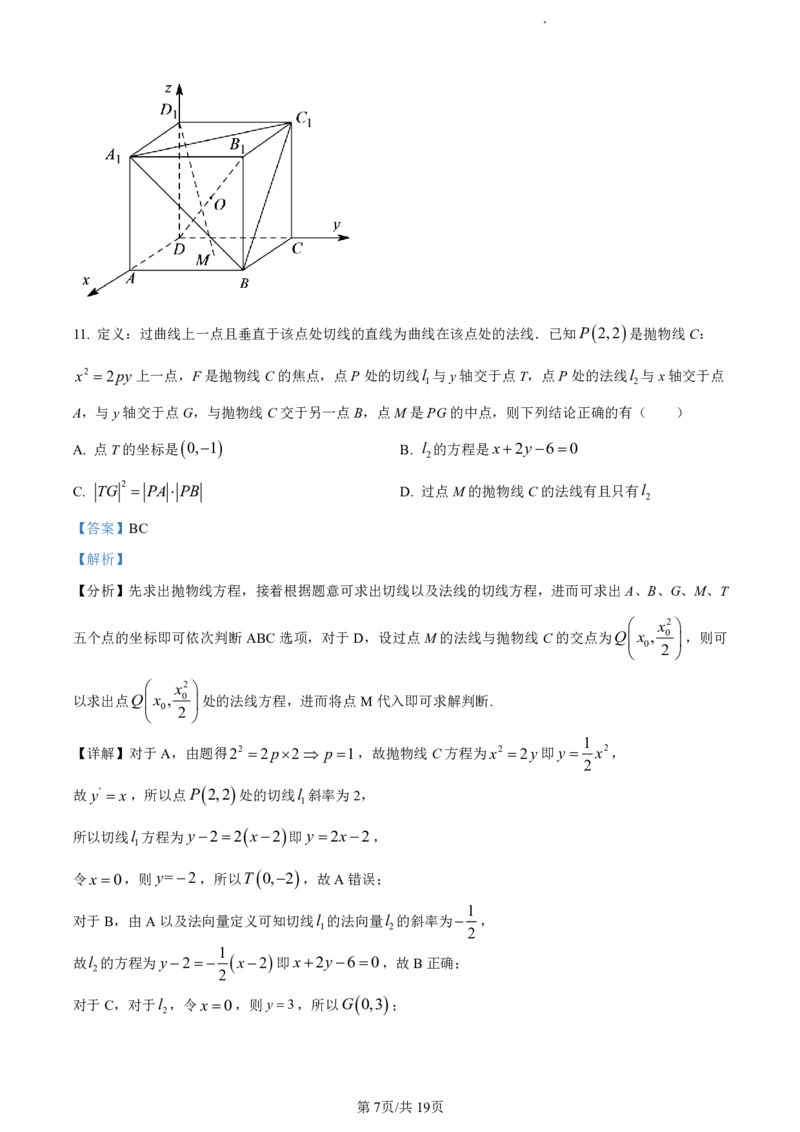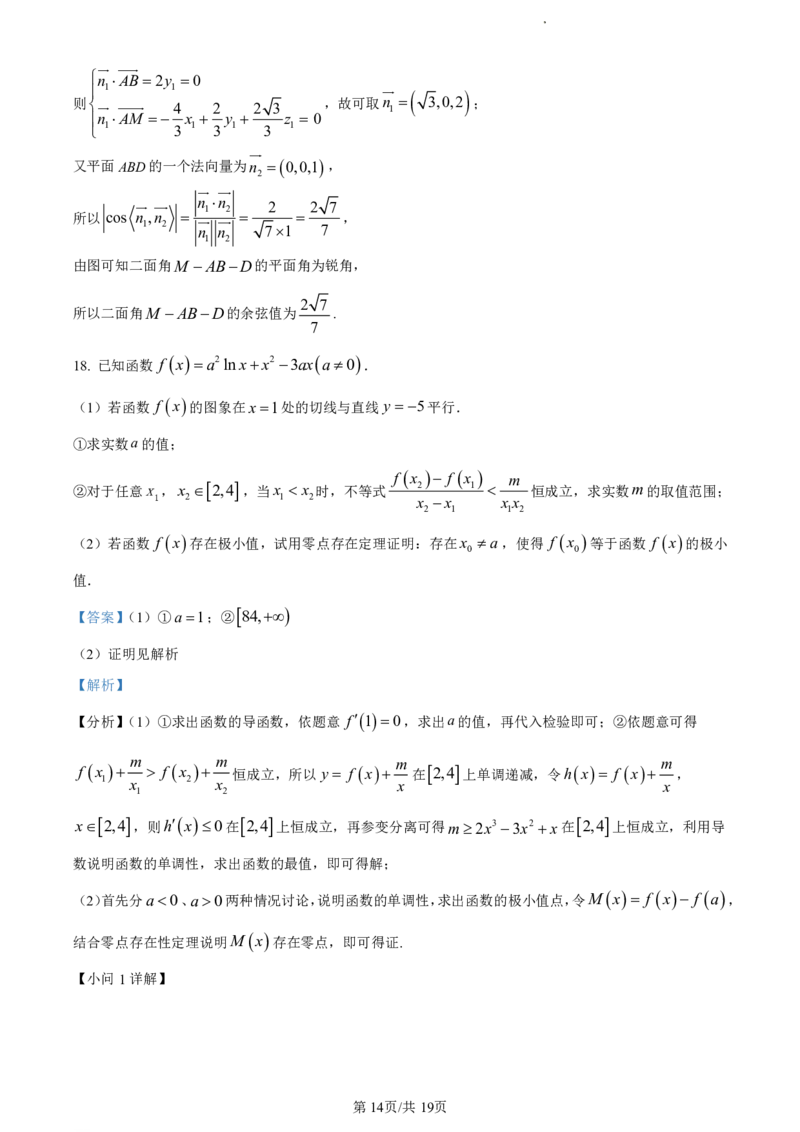江苏省盐城市2023-2024学年第二学期高二年级6月数学试题（解析版）_2024-2025高二（7-7月题库）_2024年07月试卷_0701江苏省盐城市2023-2024学年高二下学期6月期末

2023-2024 学年度第二学期高二年级期终考试
数学试题
注意事项：
1．本试卷考试时间为 120分钟，试卷满分 150分，考试形式闭卷．
2．本试卷中所有试题必须作答在答题卡上规定的位置，否则不给分．
3．答题前，务必将自己的姓名、准考证号用0.5毫米黑色墨水签字笔填写在试卷及答题卡上．
一、单选题：（本大题共 8小题，每小题 5分，计 40分．每小题给出的四个选项中，只有一
项是符合要求的，请在答题卡的指定位置填涂答案选项．）
X～N  2,2  P  X 0 0.2 P  X 4 
1. 已知随机变量 ，若 ，则 （ ）
A.0.2 B.0.3 C.0.7 D.0.8
【答案】D
【解析】
【分析】利用正态分布的对称性求概率.
【详解】随机变量X～N  2,2  ，P  X 0 0.2，
则P  X 4 P  X 0 0.2，
故P  X 4 1P  X 4 10.20.8.
故选：D.
2. 已知a   m,1  ，b   3m1,1 ，若a  //b  ，则m（ ）
A.  1 B. －1 C. 1 D. 2
2 2 3
【答案】C
【解析】
【分析】根据平面向量共线的坐标表示得到方程，解得即可.
【详解】因为a   m,1  ，b   3m1,1 且a  //b  ，
1
所以m11 3m1  ，解得m .
2
故选：C
2 1 5
3. 若随机事件A，B满足P  A  ，P  B  ，P  AB  ，则P  AB （ ）
3 2 6
第1页/共19页
学科网（北京）股份有限公司1 1 1 2
A. B. C. D.
6 3 2 3
【答案】B
【解析】
【分析】由概率的性质P  AB  P  A P  B P  AB  即可得到答案.
【详解】由概率的性质，
2 1 5 1
P  AB  P  A P  B P  AB     .
3 2 6 3
故选：B.
4. 白术是常见的大宗药材，最早记载于《神龙本草经》，又叫于术、片术，具有补脾健胃，燥湿利水等功效．今
年白术从1月份到5月份每公斤的平均价格y（单位：元）的数据如下表：
月份x 1 2 3 4 5
每公斤平均价格y 77 109 137 168 199
根据上表可得回归方程 yˆ 30xa，则实数a的值为（ ）
A.46 B.47 C.48 D.49
【答案】C
【解析】
【分析】求出x， y，根据回归直线方程必过样本中心点计算可得.
1 1
【详解】依题意x 123453， y   77109137168199 138，
5 5
 
又回归直线方程 yˆ 30xa必过样本中心点 x,y ，
所以138303a，解得a48.
故选：C
x2 y2
5. 若双曲线C：  1  a0,b0 的渐近线与圆 x2 2  y2 3没有公共点，则双曲线C的离心
a2 b2
率的取值范围为（ ）
2 3   2 3
A.   ,  B. 2, C.  1,2  D.   1,  
 3   3 
【答案】B
【解析】
【分析】先根据双曲线方程求得双曲线的渐近线，进而利用圆心到渐近线的距离大于半径求得a和b的关
第2页/共19页
学科网（北京）股份有限公司系，进而利用c2  a2 b2求得a和c的关系，则双曲线的离心率可求．
【详解】双曲线渐近线为bxay 0，且与圆 x2 2  y2 3没有公共点，
2b
圆心到渐近线的距离大于半径，即  3，
a2 b2
c
b2 3a2，b2 c2 a2 3a2，e 2．
a
故选：B．
6. 某中学开设8个社团课程，甲乙两名同学分别从这8个社团课程中随机选2个课程报名，则两人恰好有
1个课程相同的选法有（ ）
A.168种 B.336种 C.392种 D.640种
【答案】B
【解析】
【分析】先从这8个社团课程中随机选1个课程，是两名同学共同选的1个课程，然后从剩下的7个社团
课程中选2个课程，分别给甲乙两名同学，即可得到答案.
【详解】从这8个社团课程中随机选1个课程，是两名同学共同选的1个课程，方法种数为C1种，
8
从剩下的7个社团课程中选2个课程，分别给甲乙两名同学，方法种数为A2种，
7
所以共有C1A2 876336种.
8 7
故选:B.
10 1
7. 设数列  a  的前n项积为T ，满足a 3T 1，则  （ ）
n n n n T
i1 i
275 295
A.175 B.185 C. D.
2 2
【答案】A
【解析】
T 1 1
【分析】首先令n 1求出a ，当n2时a  n ，即可得到T 3TT T ，从而得到  3，
1 n T n n n1 n1 T T
n1 n n1
 1 
即 是以4为首项，3为公差的等差数列，再由等差数列求和公式计算可得.
T 
n
1
【详解】因为a 3T 1，当n 1时a 3T 1，解得a  ，
n n 1 1 1 4
第3页/共19页
学科网（北京）股份有限公司T T
当n2时a  n ，所以 n 3T 1，则T 3TT T ，
n T T n n n n1 n1
n1 n1
1 1 1  1 
所以  3，又 4，所以 是以4为首项，3为公差的等差数列，
T n T n1 T 1 T n 
10 1 10 101 
所以 410 3175.
T 2
i1 i
故选：A
8. 已知函数 f  x  x3 2x2，若 f  m 2en，则m与n的大小关系为（ ）
A. mn B. mn C. mn D. 不能确定
【答案】B
【解析】
【分析】由 f  m 2en可得nln  m3 2m2  ln2，则mnmln  m3 2m2  ln2  m2  ，令
g  m mln  m3 2m2  ln2，对g  m  求导，求出g  m  的最小值大于0，即可证明mn.
【详解】因为 f  m 2en，所以 f  m m32m2 m2 m2 2en，则m>2，
即
m3 2m2
en，两边同时取对数，则nln
m3 2m2
ln  m32m2 ln2 ，
2 2
则mnmln  m32m2  ln2mln  m32m2  ln2,  m 2 
 
令g  m mln  m3 2m2  ln2  m2  ，
3m2 4m m32m2   3m2 4m  m35m2 4m  m1  m4 
g m 1    ，
m32m2 m32m2 m32m2 m  m2 
令g
m
0，解得：m4；令g
m
0，解得：2m4，
所以在  2,4  上单调递减，在  4, 上单调递增，
g  m   g  4 4ln32ln244ln20，
min
所以mn 0，所以mn.
故选：B.
二、多选题：（本题共3个小题，每小题 6分，共 18分．在每小题给出的四个选项中，有多
项符合题目要求，全部选对的得 6分，部分选对的得部分分，有选错的得 0分．请在答题卡
的指定位置填涂答案选项．）
第4页/共19页
学科网（北京）股份有限公司9.2024年五一假期新片《维和防暴队》，《末路狂花钱》，《穿过月亮的旅行》，《九龙城寨之围城》，《间谍过
家家代号：白》，《哈尔的移动城堡》的豆瓣评分如下：5.6 ，6.2，6.7，7.5，7.5，9.1．则下列关于这
组数据的说法中正确的有（ ）
A. 均值为7.1 B. 中位数为7.1
C. 方差为2 D. 第80百分位数为7.5
【答案】ABD
【解析】
【分析】根据平均数、方差、中位数及百分位数的定义一一判断即可.
1
【详解】对于A：这组数据的均值为  5.66.26.77.57.59.1 7.1，故A正确；
6
6.77.5
对于B、D：将数据从小到大排列为5.6 ，6.2，6.7，7.5，7.5，9.1，故中位数为 7.1，
2
又680%4.8，所以第80百分位数为7.5，故B、D正确；
对于C：这组数据的方差为
1 377
 5.67.1 2  6.27.1 2  6.77.1 2 2  7.57.1 2  9.17.1 2  ，故C错误.
 
6 300
故选：ABD
10. 已知正方体ABCDABCD 的棱长为1，M 为平面ABCD内一动点，则下列结论正确的有（ ）
1 1 1 1
A. BD 平面AC B
1 1 1
π
B. 若直线DM 与平面ABCD所成角为 ，则点M 的轨迹是椭圆
1
3
  1 1
C. 存在点M ，使得DM  DD DA DC
1 1 2 2
2
D. 正方体ABCDABCD 的外接球被平面AC B所截得的截面面积为 π
1 1 1 1 1 1 3
【答案】ACD
【解析】
【分析】建立空间直角坐标系，利用空间向量法一一计算可得.
       
【详解】如图建立空间直角坐标系，则D 0,0,0 ，B 1,1,0 ，A 1,0,1 ，C 0,1,1 ，
1 1
       
D 0,0,1 ，C 0,1,0 ，A 1,0,0 ，B 1,1,1 ，
1 1
  
所以AC 1,1,0 ，BA  0,1,1 ，DB  1,1,1 ，
1 1 1 1
       
所以DB AC 0，DB BA 0，所以DB  AC ，DB BA ，
1 1 1 1 1 1 1 1 1 1
第5页/共19页
学科网（北京）股份有限公司即DB  AC ，DB  BA ，又BA AC  A ，BA,AC 平面AC B，
1 1 1 1 1 1 1 1 1 1 1 1 1 1
所以BD 平面AC B，故A正确；
1 1 1
 
设M  x,y,0  ，则DM  x,y,1 ，又平面ABCD的法向量可以为n  0,0,1  ，
1


  D 1 M n 1 3 1
依题意 cosDM,n     ，所以x2  y2  ，
1 DM  n  x2  y2 1 2 3
1
π
所以直线DM 与平面ABCD所成角为 ，则点M 的轨迹是圆，故B错误；
1
3
 1 1 1 1 1 1 
因为DD DA DC  0,0,1   1,0,0   0,1,0   , ,1，
1 2 2 2 2 2 2 
 1   1 1
DM  x,y,1 ，所以当x y 时满足DM  DD DA DC，故C正确；
1 2 1 1 2 2
正方体ABCDABCD 的外接球的直径为正方体的体对角线，
1 1 1 1
12 12 12 3 1 1 1
则外接球的半径R   ，球心为DB 的中点，设为O，则O , , ，
2 2 1 2 2 2


由BD 平面AC B，所以平面AC B的一个法向量为m DB  1,1,1 ，
1 1 1 1 1 1
  1 1 1
又BO    , , ，
 2 2 2
 1

mBO
所以点O到平面AC B的距离 2 3 ，
1 1 d    
m 3 6
设平面AC B被外接球所截的截面圆的半径为r，
1 1
2 2
 3  3 2
则r  R2 d2       ，
   
2 6 3
   
2
所以截面圆的面积S  πr2  π，故D正确.
3
故选：ACD
第6页/共19页
学科网（北京）股份有限公司 
11. 定义：过曲线上一点且垂直于该点处切线的直线为曲线在该点处的法线．已知P 2,2 是抛物线C：
x2 2py 上一点，F是抛物线C的焦点，点P处的切线l 与y轴交于点T，点P处的法线l 与x轴交于点
1 2
A，与y轴交于点G，与抛物线C交于另一点B，点M是PG的中点，则下列结论正确的有（ ）
A. 点T的坐标是  0,1  B. l 的方程是x2y60
2
C. TG 2  PA  PB D. 过点M的抛物线C的法线有且只有l
2
【答案】BC
【解析】
【分析】先求出抛物线方程，接着根据题意可求出切线以及法线的切线方程，进而可求出A、B、G、M、T
 x2 
五个点的坐标即可依次判断ABC选项，对于D，设过点M的法线与抛物线C的交点为Qx , 0 ，则可
 0 2 
 x2 
以求出点Qx , 0 处的法线方程，进而将点M代入即可求解判断.
 0 2 
1
【详解】对于A，由题得22 2p2 p1，故抛物线C方程为x2 2y即y  x2，
2
故 y  x，所以点P  2,2  处的切线l 斜率为2，
1
所以切线l 方程为 y22  x2  即 y 2x2，
1
令x0，则 y=2，所以T  0,2  ，故A错误；
1
对于B，由A以及法向量定义可知切线l 的法向量l 的斜率为 ，
1 2
2
1
故l 的方程为 y2  x2 即x2y60，故B正确；
2
2
 
对于C，对于l ，令x0，则y3，所以G 0,3 ；
2
第7页/共19页
学科网（北京）股份有限公司 
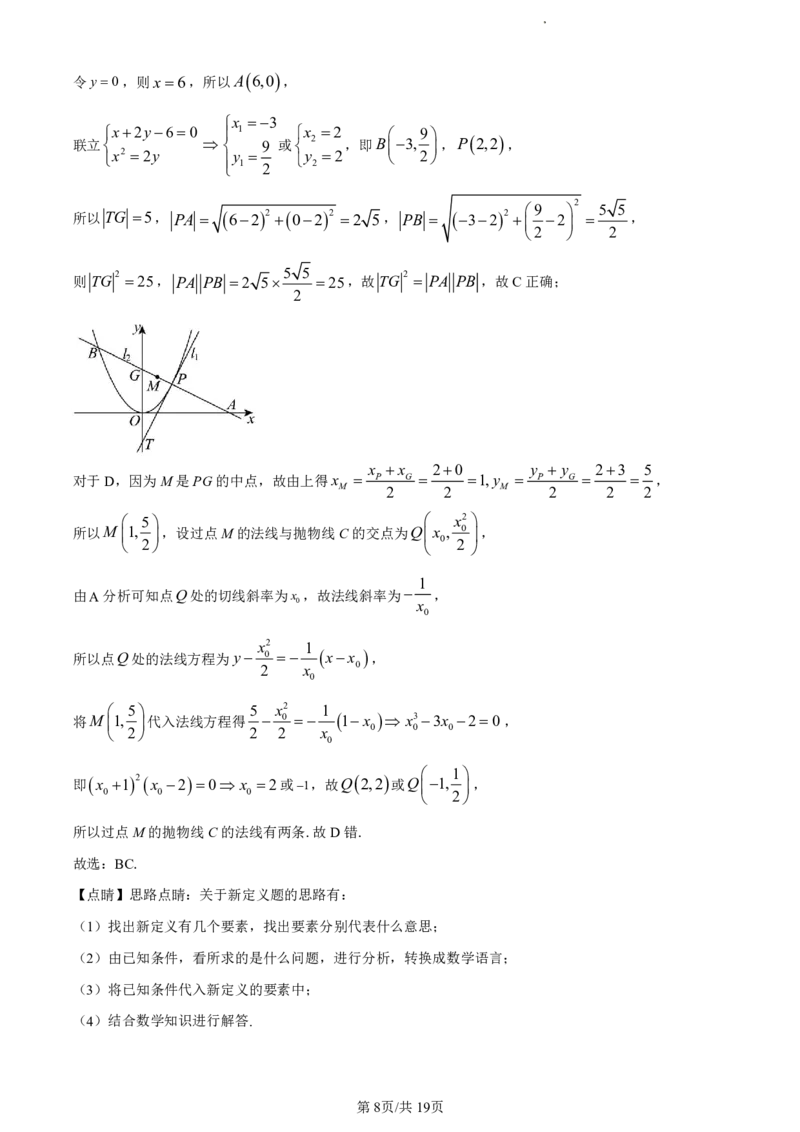
令y0，则x6，所以A 6,0 ，
x 3
x2y60  1 x 2  9
联立   9 或 2 ，即B 3, ，P  2,2  ，
x2 2y y  y 2  2
 1 2 2
2
9  5 5
所以 TG 5， PA   62 2  02 2 2 5， PB  32 2   2  ，
2  2
则 TG 2 25， PA PB 2 5 5 5 25，故 TG 2  PA PB ，故C正确；
2
x x 20 y  y 23 5
对于D，因为M是PG的中点，故由上得x  P G  1,y  P G   ，
M 2 2 M 2 2 2
 5  x2 
所以M 1, ，设过点M的法线与抛物线C的交点为Qx , 0 ，
 2  0 2 
1
由A分析可知点Q处的切线斜率为x ，故法线斜率为 ，
0 x
0
x2 1
所以点Q处的法线方程为 y 0   xx  ，
2 x 0
0
 5 5 x2 1
将M 1, 代入法线方程得  0   1 x  x33x 2 0，
 2 2 2 x 0 0 0
0
 1
即 x 1 2 x 2 0 x 2或1，故Q  2,2  或Q 1, ，
0 0 0  2
所以过点M的抛物线C的法线有两条.故D错.
故选：BC.
【点睛】思路点睛：关于新定义题的思路有：
（1）找出新定义有几个要素，找出要素分别代表什么意思；
（2）由已知条件，看所求的是什么问题，进行分析，转换成数学语言；
（3）将已知条件代入新定义的要素中；
（4）结合数学知识进行解答.
第8页/共19页
学科网（北京）股份有限公司三、填空题（本大题共 3小题，每小题 5分，计15分．第 14题第一空 2分，第二空 3分．不
需写出解答过程，请把答案写在答题卡的指定位置上）
12.  1x 3  1x 4  1x 5  1x 6展开式中含x2项的系数为______．
【答案】34
【解析】
【分析】求出各项展开中的x2系数，再求和即可.
【详解】x2的系数分别为C2、C2、C2、C2，
3 4 5 6
故展开式中x2的系数和为C2+C2+C2+C2 34.
3 4 5 6
故答案为：34.
13. 一种抛掷骰子游戏：若抛掷出点数为1，2，则得0分；若抛掷出点数为3，4，5，6，则得2分．现抛
掷骰子10次，则得分X的期望值为______．
40 1
【答案】 ##13
3 3
【解析】
【分析】设抛掷骰子一次得分为Y ，求出Y 的可能取值及其对应的概率，即可求出EY ，又X 10Y，由
均值的性质即可得出答案.
【详解】设抛掷骰子一次得分为Y ，则Y 0,2，
2 1 4 2
P  Y 0   ，P  Y 2   ，
6 3 6 3
1 2 4
所以E  Y 0 2  ，因为X 10Y，
3 3 3
4 40
所以E  X  E  10Y 10E  Y 10  .
3 3
40
故答案为： .
3
14. 祖暅，祖冲之之子，他的“祖暅原理”﹔幂势既同，则积不容异．意思是：夹在两个平行平面之间的两个
几何体，被平行于这两个平面的任意平面所截，如果截得的面积总相等，那么这两个几何体的体积相等．将
x2 y2
双曲线E：  1与y0，y 5所围成的平面图形（含边界）绕其虚轴旋转一周得到如图所示的几何
9 25
体，其中线段OA为双曲线的实半轴，直线 y 5分别与双曲线E的一条渐近线及右支交于点B和C，则
线段BC旋转一周所得图形的面积为______，几何体的体积为______．
第9页/共19页
学科网（北京）股份有限公司【答案】 ①. 9 ②. 60π
【解析】
   
【分析】根据已知可得B 3,5 ，C 3 2,5 ，则线段BC旋转一周所得的图形为圆环面积，可得其面积；
根据祖暅定理可知几何体的体积为一个截面积相同的几何体体积加上等高的圆锥体积，即可得到答案.
【详解】
x2 y2 5
由双曲线  1得a 3,b5，则渐近线方程为 y  x，
9 25 3
 5 x2 y2
所以   y  3 x    x 3 ，则B  3,5  ；又   9  25 1    x3 2 ，则C  3 2,5  ，
 y 5 y 5  y 5 y 5
 2
则线段旋转一周所得的图形的面积为：S  3 2 π32π 9π；
1
设在直线y0和y 5之间的任一条直线 y t0t 5，分别与双曲线E的一条渐近线及右支交于点G
和F，
 5  3 x2 y2  3
y  x x  t 3    1 x 25t2 3 
由 3  5 ，则G t,t，又 9 25  5 ，则F 25t2,t，
 y t  y t 5   y t  y t 5 
2 2
3  3 
则线段GF 旋转一周所得的图形的面积为：S  25t2  π  t π 9π，
5  5 
则被平行于这两个平面的任意平面所截，两个截面的面积总相等，
又双曲线的实半轴OAa3，此时截面面积为S  π32 9π  S ，
2 1
1
所以根据祖暅定理可得,几何体的体积为V  S hV 9π5 π32560π.
1 圆锥 3
第10页/共19页
学科网（北京）股份有限公司故答案为：9；60π.
四、解答题（本大题共 6小题，计 77分．解答应写出必要的文字说明，证明过程或演算步骤，
请把答案写在答题卡的指定区域内）
15. 盒中有四张卡片，分别标有数字1，2，3，4，现从盒中任取两张卡片，记取到偶数的个数为X ．
（1）求P  X 1  ；
（2）求X 的分布列．
2
【答案】（1）
3
（2）分布列见解析
【解析】
【分析】（1）利用古典概型的概率公式计算可得；
（2）依题意X 的可能取值为0，1，2，求出所对应的概率，即可得到分布列.
【小问1详解】
X 1表示的随机事件是“取到的两张卡片上的数字是一个偶数、一个奇数”，
C1 C1 2
所以P  X 1  2 2  ；
C2 3
4
【小问2详解】
依题意X 的可能取值为0，1，2，
C2 1 C1 C1 2 C2 1
则P  X 0  2  ，P  X 1  2 2  ，P  X 2  2  ，
C2 6 C2 3 C2 6
4 4 4
所以X 的分布列如下所示：
X 0 1 2
1 2 1
P
6 3 6
16. 已知数列  a  是正项等比数列，其前n项和为S ，且a a 12，S  S 108．
n n 1 2 4 2
 
（1）求 a 的通项公式；
n
a
（2）设b  n ，求满足b 100的最大整数n．
n log a n
3 n
【答案】（1）a 3n
n
第11页/共19页
学科网（北京）股份有限公司（2）5
【解析】
a a 12
【分析】（1）设等差数列的公比为q，则 1 2 ，解方程即可得出答案；
S S 108
4 2
 
（2）由（1）求出b ，求得 b 在nN*上单调递增，b 100,b 100，即可得出答案；
n n 5 6
【小问1详解】
a a 12
设等差数列的公比为q，则 1 2 ，
S S 108
4 2
a a q12
则 1 1 ，因为q0，所以q 3，a 3，
a q2 a q3 108 1
1 1
所以a a qn1 33n1 3n .
n 1
【小问2详解】
a 3n 3n
因为a 3n，b  n   ，
n n log a log 3n n
3 n 3
3n1
b n1  n1  3n1  n  3n 1，所以  b  在nN*上单调递增，
b 3n n1 3n n1 n
n
n
36 729 35
b   100,b  100，满足b 100的最大整数为5.
6 6 6 5 5 n
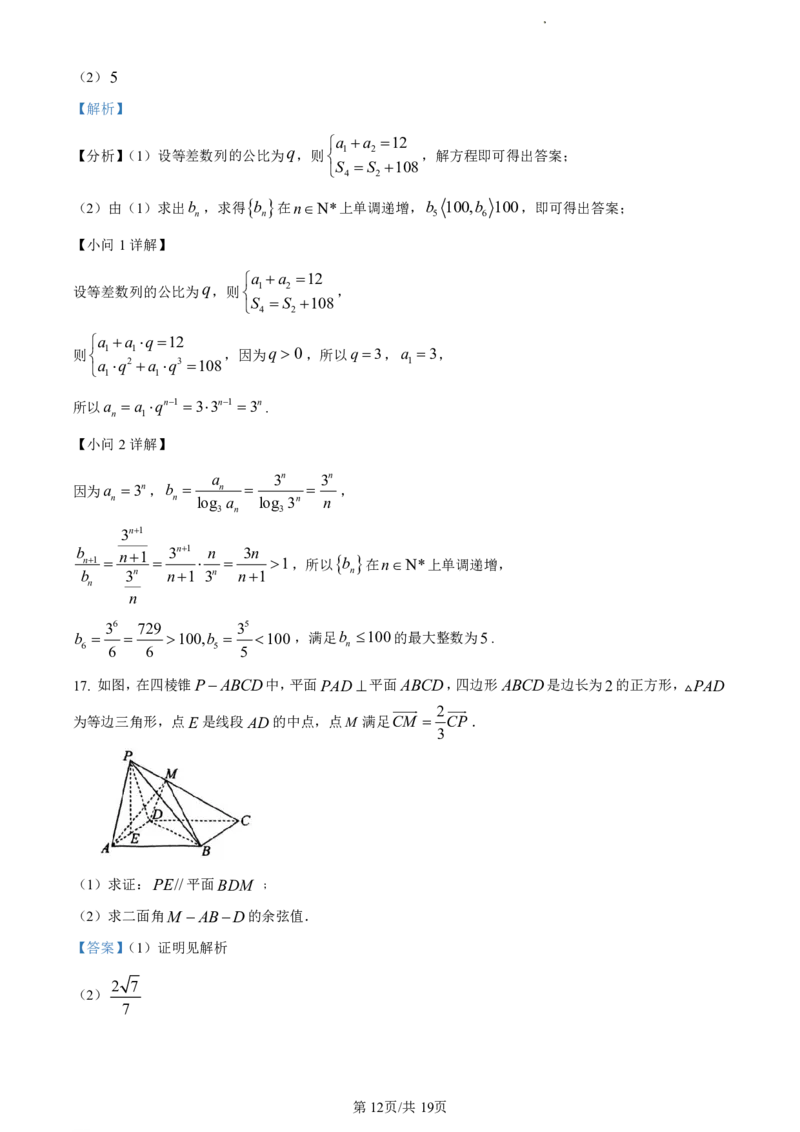
17. 如图，在四棱锥PABCD中，平面PAD 平面ABCD，四边形ABCD是边长为2的正方形，PAD
 2
为等边三角形，点E是线段AD的中点，点M 满足CM  CP ．
3
（1）求证：PE//平面BDM ﹔
（2）求二面角M ABD的余弦值．
【答案】（1）证明见解析
2 7
（2）
7
第12页/共19页
学科网（北京）股份有限公司【解析】
【分析】（1）连接EC交BD于N ，连接MN，根据条件证明MN//PE 即可得证；
（2）先证明PE 平面ABCD，建立空间直角坐标系，求出相关点和向量的坐标，分别求得平面AMB与
平面ABD的法向量，最后由空间向量的夹角公式求解即得.
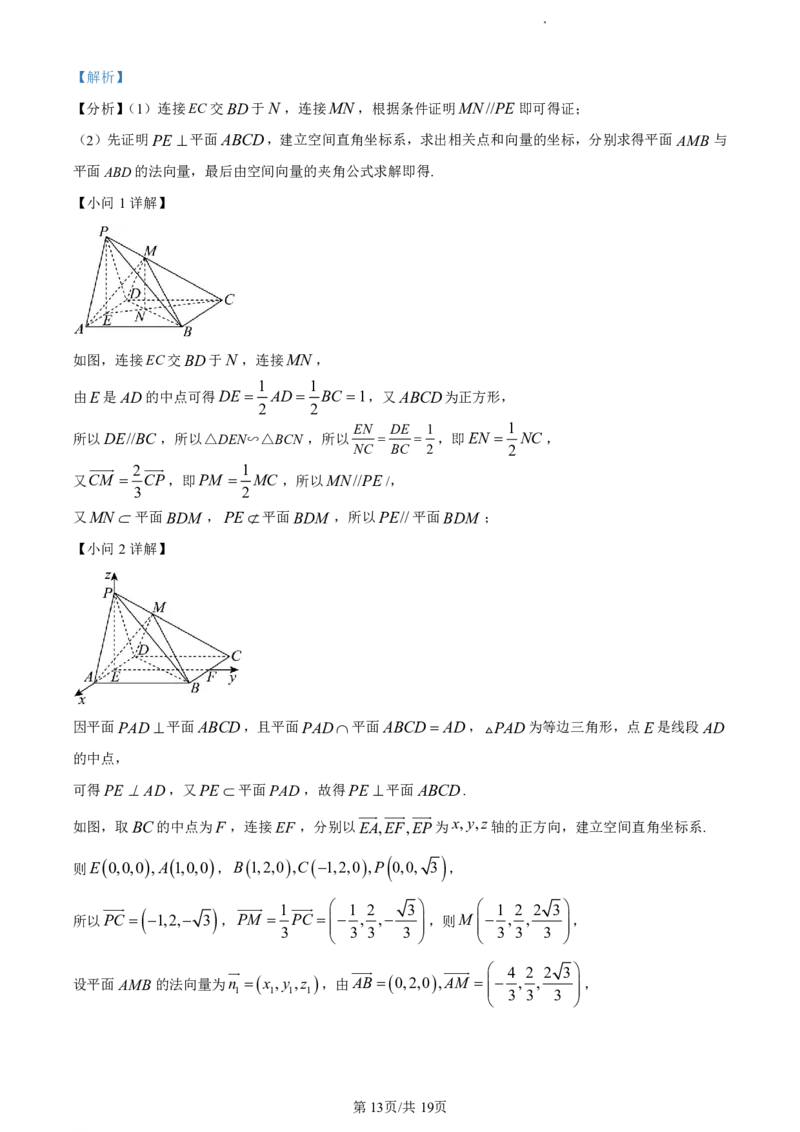
【小问1详解】
如图，连接EC交BD于N ，连接MN，
1 1
由E是AD的中点可得DE  AD  BC 1，又ABCD为正方形，
2 2
EN DE 1 1
所以DE//BC ，所以△DEN∽△BCN ，所以   ，即EN  NC ，
NC BC 2 2
 2 1
又CM  CP，即PM  MC ，所以MN//PE /，
3 2
又MN平面BDM ，PE平面BDM ，所以PE//平面BDM ；
【小问2详解】
因平面PAD 平面ABCD，且平面PAD平面ABCD AD，PAD为等边三角形，点E是线段AD
的中点，
可得PEAD，又PE 平面PAD，故得PE 平面ABCD.
  
如图，取BC的中点为F ，连接EF ，分别以EA,EF,EP为x,y,z轴的正方向，建立空间直角坐标系.
则E  0,0,0  ,A  1,0,0  ，B  1,2,0  ,C 1,2,0  ,P  0,0, 3  ，
    1  1 2 3  1 2 2 3
所以PC  1,2, 3 ，PM  PC  , , ，则M  , , ，
   
3 3 3 3 3 3 3
   
    4 2 2 3
设平面AMB的法向量为n  x ,y ,z ，由AB  0,2,0  ,AM  , , ，
1 1 1 1  3 3 3 
 
第13页/共19页
学科网（北京）股份有限公司 
n AB  2y 0
 1 1   
则  4 2 2 3 ，故可取n 1  3,0,2 ；
n AM  x  y  z  0
 1 3 1 3 1 3 1

又平面ABD的一个法向量为n  0,0,1 ，
2
 
  n 1 n 2 2 2 7
所以 cos n ,n      ，
1 2 n n 71 7
1 2
由图可知二面角M ABD的平面角为锐角，
2 7
所以二面角M ABD的余弦值为 .
7
18. 已知函数 f  x a2lnxx2 3ax  a0  ．
（1）若函数 f  x  的图象在x 1处的切线与直线 y 5平行．
①求实数a的值；
f

x

f

x

m
②对于任意x，x  2,4  ，当x  x 时，不等式 2 1  恒成立，求实数m的取值范围；
1 2 1 2 x x x x
2 1 1 2
（2）若函数 f  x  存在极小值，试用零点存在定理证明：存在x a，使得 f  x  等于函数 f  x  的极小
0 0
值．
【答案】（1）①a 1；②
 84,
（2）证明见解析
【解析】
【分析】（1）①求出函数的导函数，依题意
f
1
0，求出a的值，再代入检验即可；②依题意可得
f  x  m  f  x  m 恒成立，所以 y  f  x  m 在  2,4  上单调递减，令h  x  f  x  m ，
1 x 2 x x x
1 2
x
2,4
 ，则h
x
0在 
2,4

上恒成立，再参变分离可得m2x33x2 x在

2,4

上恒成立，利用导
数说明函数的单调性，求出函数的最值，即可得解；
（2）首先分a0、a0两种情况讨论，说明函数的单调性，求出函数的极小值点，令M

x

f

x

f

a

，
 
结合零点存在性定理说明M x 存在零点，即可得证.
【小问1详解】
第14页/共19页
学科网（北京）股份有限公司①函数 f  x a2lnxx2 3ax  a0  的定义域为  0, ， f x 
a2
2x3a，
x
因为函数 f  x  的图象在x 1处的切线与直线 y 5平行，即 f 1 a2 23a0，解得a 1或a2；
当a 1时 f  x lnxx2 3x，则 f (1)=-2，
则函数 f  x  的图象在x 1处的切线为y=2，与直线 y 5平行，符合题意；
当a2时 f  x 4lnxx2 6x，则 f  1 5，
则函数 f  x  的图象在x 1处的切线为y 5，与直线 y 5重合，不符合题意；
所以a 1.
f

x

f

x

m
②对于任意x，x  2,4  ，当x  x 时，不等式 2 1  恒成立，
1 2 1 2 x x x x
2 1 1 2
m m
即 f  x   f  x  恒成立，
1 x 2 x
1 2
m
所以 y  f  x  在  2,4  上单调递减，
x
m m
令h  x  f  x  lnxx2 3x ，x 2,4  ，
x x
1 m
则h x  2x3 0在  2,4  上恒成立，
x x2
 
所以m2x33x2 x在 2,4 上恒成立，
令F  x 2x33x2 x，x 2,4  ，
2
则F x 6x2 6x16  x 1   1 在  2,4  上单调递递增，
 2 2
所以F
x
 F
2
0，
所以F  x  在  2,4  上单调递递增，所以F  x   F  4 84，
max
所以m84，即实数m的取值范围为  84, ；
【小问2详解】
函数 f  x a2lnxx2 3ax  a0  的定义域为  0, ，
a2  xa  2xa 
且 f x  2x3a  ，
x x
第15页/共19页
学科网（北京）股份有限公司当a0时 f¢(x)>0恒成立，所以 f  x  在  0, 上单调递增，则 f  x  无极值，不符合题意；
当a0时x， f  x  ， f  x  的关系如下所示：
 a a a 
x 0,   ,a a
 a,
 2 2 2 
f  x   0  0 
 
f x 单调递增 极大值 单调递减 极小值 单调递增
所以 f  x  在xa处取得极小值，
 x
令M  x  f  x  f  a a2lnxx2 3ax f  a a2ln  x2 3ax2a2，
a
 a  a  a  a 3 
则M     3a 0，M     ln2a2 0，
e2  e2 e2  2 4 
3
（e3 2.73 19.68324，所以lne3 ln24，则34ln2，所以 ln2），
4
 a  a  a a
所以M  M   0，又M  x  在 , 上为连续函数，
e2  2 e2 2
 a a
 
所以M x 在 , 上存在零点x ，
e2 2 0
 a a
即x   , 使得M  x 0，此时 f  x  f  a  ，
0 e2 2 0 0
所以存在x a，使得 f  x  等于函数 f  x  的极小值.
0 0
【点睛】方法点睛：导函数中常用的两种常用的转化方法：一是利用导数研究含参函数的单调性，常化为
不等式恒成立问题．注意分类讨论与数形结合思想的应用；二是函数的零点、不等式证明常转化为函数的
单调性、极(最)值问题处理．
x2 y2 2
19. 在平面直角坐标系xoy中，已知椭圆E：  1  ab0 的离心率为 ，右焦点F到椭圆E上
a2 b2 3
任意一点的最小距离为1．
（1）求椭圆E的方程；
（2）设A，B为椭圆E的左，右顶点，过点F作直线l交椭圆E于C，D两点，C与A，B不重合），连接AC，
第16页/共19页
学科网（北京）股份有限公司BD交于点Q．
①求证：点Q在定直线上：
    5 1
②设AQ AC，BQ BD，求  的最大值．
1 2  
1 2
x2 y2
【答案】（1）  1
9 5
9 5 1 8
（2）①点Q在定直线x 上；②  的最大值为
2   3
1 2
【解析】
【分析】（1）根据椭圆离心率公式、焦半径范围和a2 b2 c2求出a、b即可得解.
（2）①先由（1）得A 3,0  ，B  3,0  ，F  2,0  ，设直线l:x ty2、C  x ,y  、D  x ,y  ，
1 1 2 2
y y
则可得l : y  1  x3  ，l : y  2  x3  ，结合点C、D在直线l上联立直线AC与直线BD
AC x 3 BD x 3
1 2
得Q点横坐标是一个定值从而得解.
    15 3
②由①以及AQ AC，BQ BD可分别求出 和  ，结合（1）中韦达定
1 2 1 2  x 3  2 2  x 3 
1 2
5 1
理将其直接带入  计算即可求解.
 
1 2
【小问1详解】
a2 b2 c2

c 2
由题意得  ，a 3,b 5,c2，
a 3

ac1

x2 y2
所以椭圆E的方程为  1.
9 5
【小问2详解】
①由（1）A 3,0  ，B  3,0  ，F  2,0  ，故可设直线l:x ty2，
xty2

 
联立x2 y2  5t29 y2 20ty250，

 1
 9 5
第17页/共19页
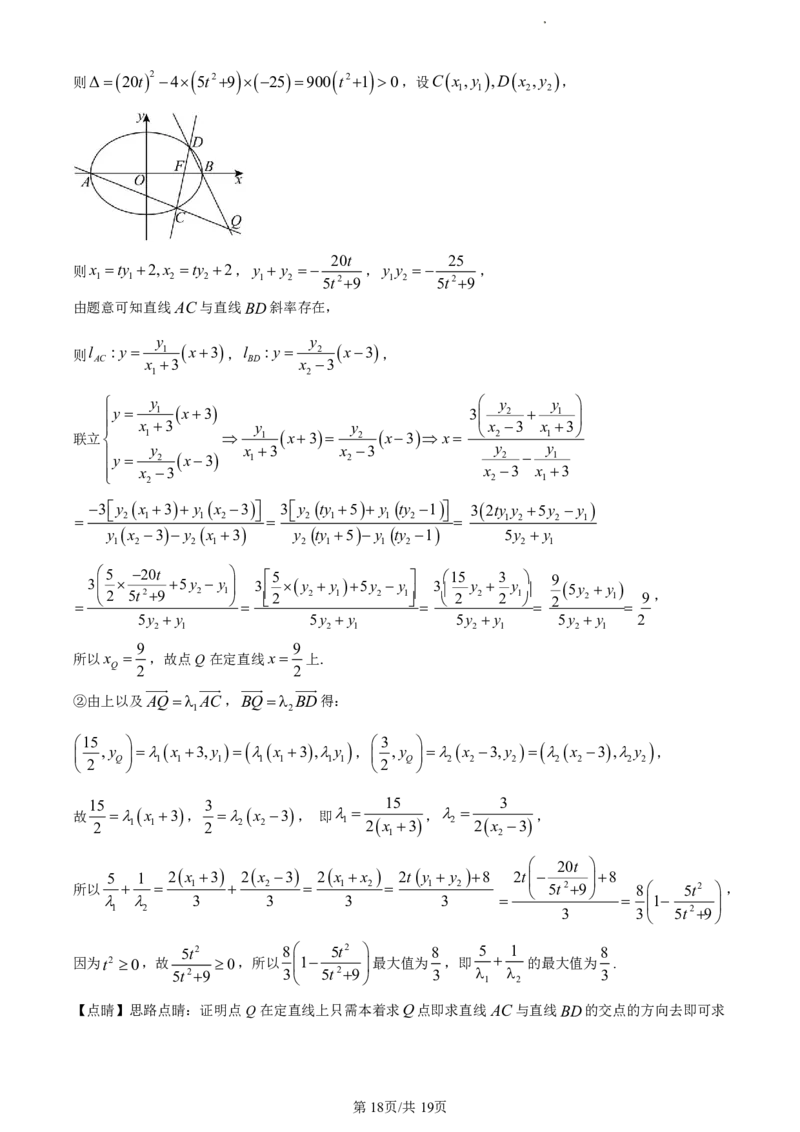
学科网（北京）股份有限公司则Δ 20t 2 4  5t29  25 900  t21  0，设C  x ,y  ,D  x ,y  ，
1 1 2 2
20t 25
则x ty 2,x ty 2，y  y  ，y y  ，
1 1 2 2 1 2 5t29 1 2 5t29
由题意可知直线AC与直线BD斜率存在，
y y
则l : y  1  x3  ，l : y  2  x3  ，
AC x 3 BD x 3
1 2
 y  y y 
 y  1  x3  3 2  1 
 x 3 y y  x 3 x 3
联立 1  1  x3  2  x3  x 2 1
y x 3 x 3 y y
 y  2  x3  1 2 2  1
  x 2 3 x 2 3 x 1 3
3  y  x 3  y  x 3   3  y  ty 5  y  ty 1   3  2ty y 5y y 
 2 1 1 2  2 1 1 2  1 2 2 1
y  x 3 y  x 3  y  ty 5 y  ty 1  5y  y
1 2 2 1 2 1 1 2 2 1
3    5 2  5  t 2 2 0  t 9 5y 2  y 1    3    5 2  y 2  y 1 5y 2  y 1   3    1 2 5 y 2  3 2 y 1   9 2  5y 2  y 1  9，
    
5y  y 5y  y 5y  y 5y  y 2
2 1 2 1 2 1 2 1
9 9
所以x  ，故点Q在定直线x 上.
Q 2 2
   
②由上以及AQ AC，BQ BD得：
1 2
15  3 
 ,y   x 3,y    x 3  ,y  ， ,y   x 3,y    x 3  ,y  ，
 2 Q  1 1 1 1 1 1 1 2 Q  2 2 2 2 2 2 2
15 3 15 3
故  x 3 ，  x 3 ， 即 ，  ，
2 1 1 2 2 2 1 2  x 3  2 2  x 3 
1 2
 20t 
5 1 2  x 3  2  x 3  2  x x  2t  y  y 8 2t 8
所以   1  2  1 2  1 2  5t29 8 5t2 ，
  3 3 3 3   1 
1 2 3 3 5t29
5t2 8 5t2  8 5 1 8
因为t2 0，故 0，所以 1 最大值为 ，即  的最大值为 .
5t29 3 5t29 3   3
1 2
【点睛】思路点睛：证明点Q在定直线上只需本着求Q点即求直线AC与直线BD的交点的方向去即可求
第18页/共19页
学科网（北京）股份有限公司解.
第19页/共19页
学科网（北京）股份有限公司