文档内容
2023-2024 学年度第一学期高三年级期中质量调查(数学)试卷
满分:150分 时长:120分钟
第I卷(选择题)
一、单选题(本大题共10小题,共50.0分.在每小题列出的选项中,选出符合题目的一项)
1. 已知全集 ,集合 , ,则 为
A. {1,2,4} B. {2,3,4} C. {0,2,4} D. {0,2,3,4}
2. “ ”是“ ”的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
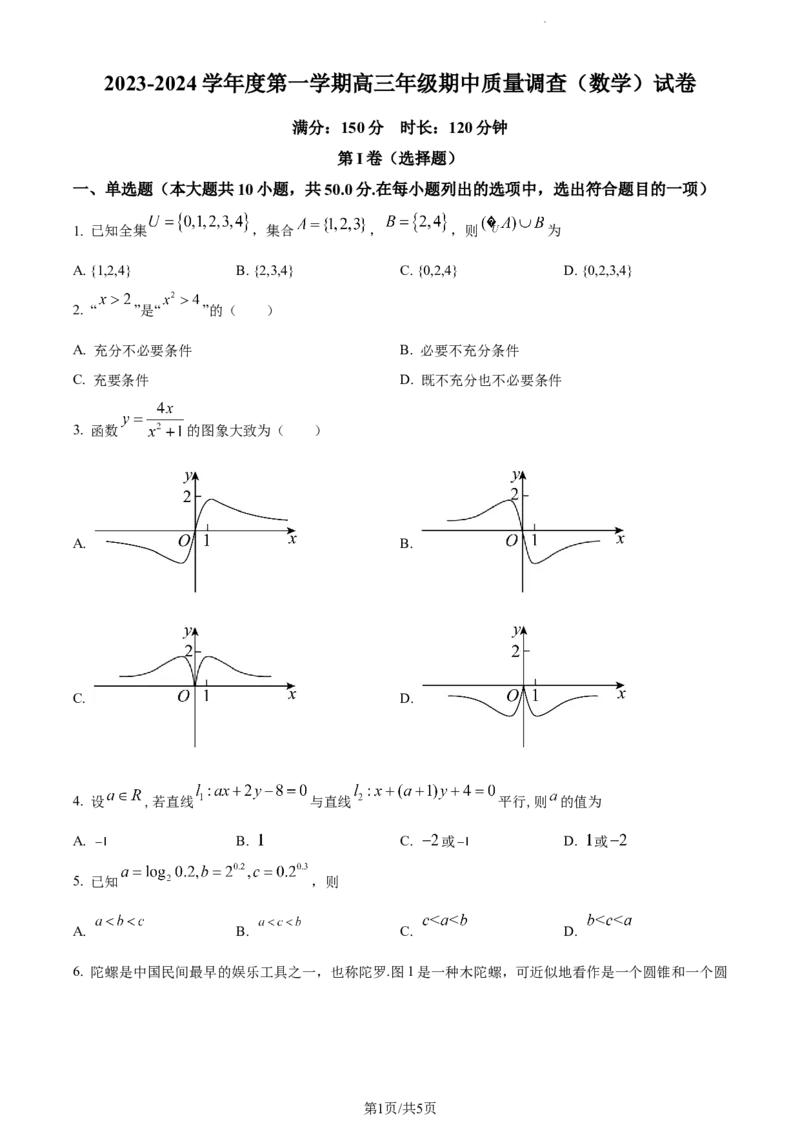
3. 函数 的图象大致为( )
A. B.
C. D.
4. 设 ,若直线 与直线 平行,则 的值为
A. B. C. 或 D. 或
5. 已知 ,则
A. B. C. D.
6. 陀螺是中国民间最早的娱乐工具之一,也称陀罗.图1是一种木陀螺,可近似地看作是一个圆锥和一个圆
第1页/共5页
学科网(北京)股份有限公司柱的组合体,其直观图如图2所示,其中 分别是上、下底面圆的圆心,且 ,底面圆的
半径为2,则该陀螺的体积是( )
A. B. C. D.
7. 设点 、 ,若直线l过点 且与线段AB相交,则直线l的斜率k的取值范围是(
)
A. 或 B. 或
C. D.
8. 已知函数 的图象向左平移 个单位长度后得到函数
的图象,则φ的可能值为( )
A. 0 B. C. D.
9. 已知双曲线 ( , )的左,右焦点分别为 , .若双曲线右支上存在点 ,使
得 与双曲线的一条渐近线垂直并相交于点 ,且 ,则双曲线的渐近线方程为( )
.
A B. C. D.
第2页/共5页
学科网(北京)股份有限公司10. 对 ,当 时, ,则实数 的取值范围是( )
A. B. C. D.
二、填空题(本大题共8小题,共40.0分)
11. 已知 (i为虚数单位),则 ___________.
12. 已知向量 , ,若 ,则实数k的值为______.
13. 已知 , ,则 的值为________.
14. 圆心在直线 上且与直线 相切于点 的圆的方程是________.
15. 以双曲线 的焦点为顶点,顶点为焦点的椭圆方程为________.
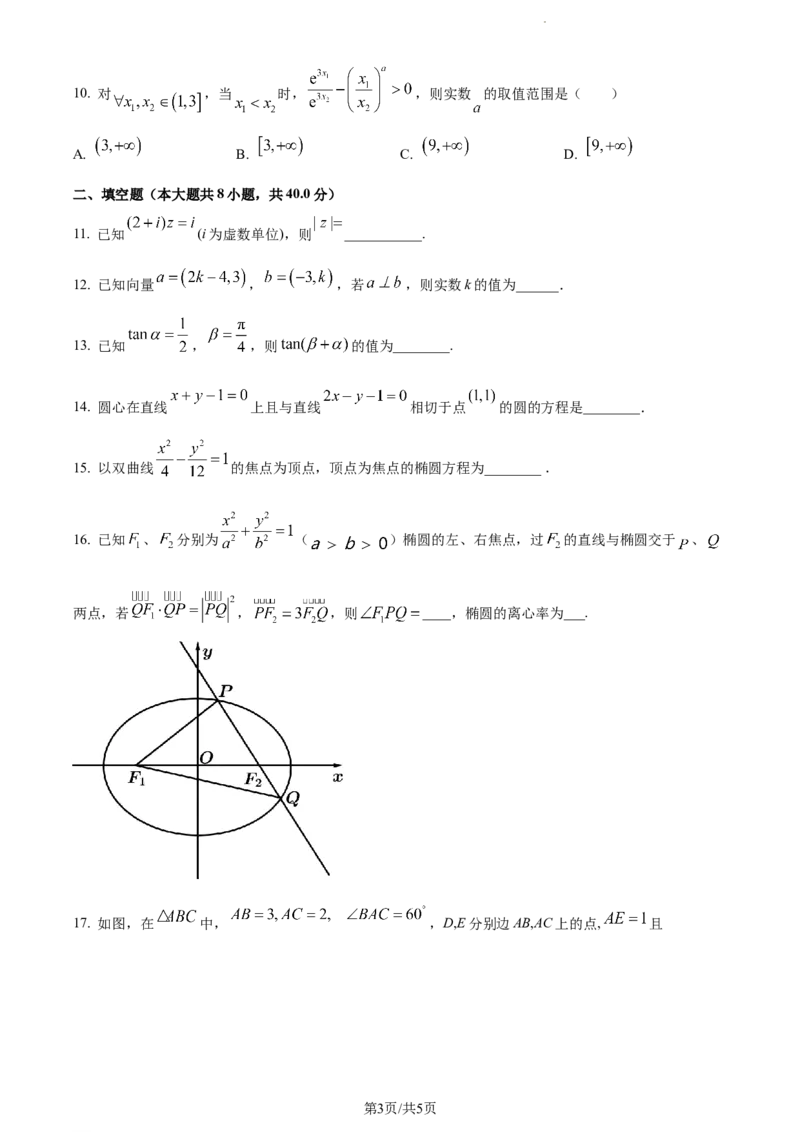
16. 已知 、 分别为 ( )椭圆的左、右焦点,过 的直线与椭圆交于 、
两点,若 , ,则 ____,椭圆的离心率为___.
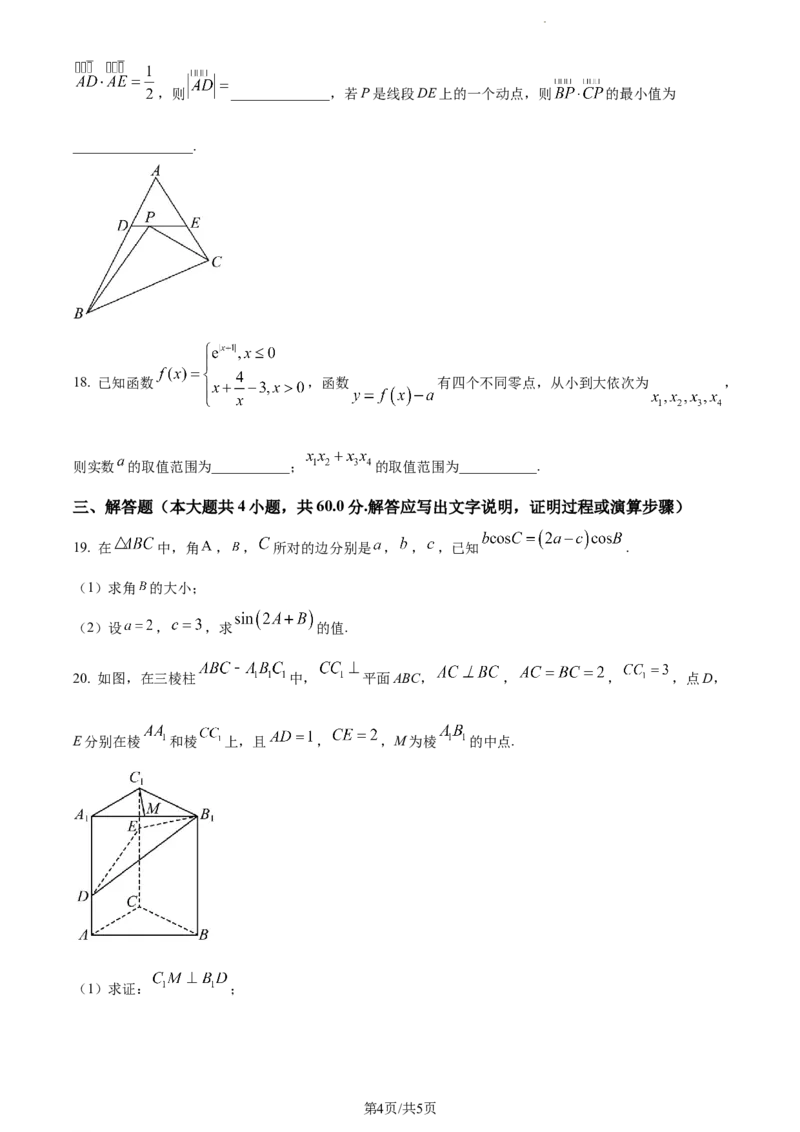
17. 如图,在 中, ,D,E分别边AB,AC上的点, 且
第3页/共5页
学科网(北京)股份有限公司,则 ______________,若P是线段DE上的一个动点,则 的最小值为
_________________.
18. 已知函数 ,函数 有四个不同零点,从小到大依次为 ,
则实数 的取值范围为___________; 的取值范围为___________.
三、解答题(本大题共4小题,共60.0分.解答应写出文字说明,证明过程或演算步骤)
19. 在 中,角 , , 所对的边分别是 , , ,已知 .
(1)求角 的大小;
(2)设 , ,求 的值.
20. 如图,在三棱柱 中, 平面ABC, , , ,点D,
E分别在棱 和棱 上,且 , ,M为棱 的中点.
(1)求证: ;
第4页/共5页
学科网(北京)股份有限公司(2)求直线AB与平面 所成角的正弦值.
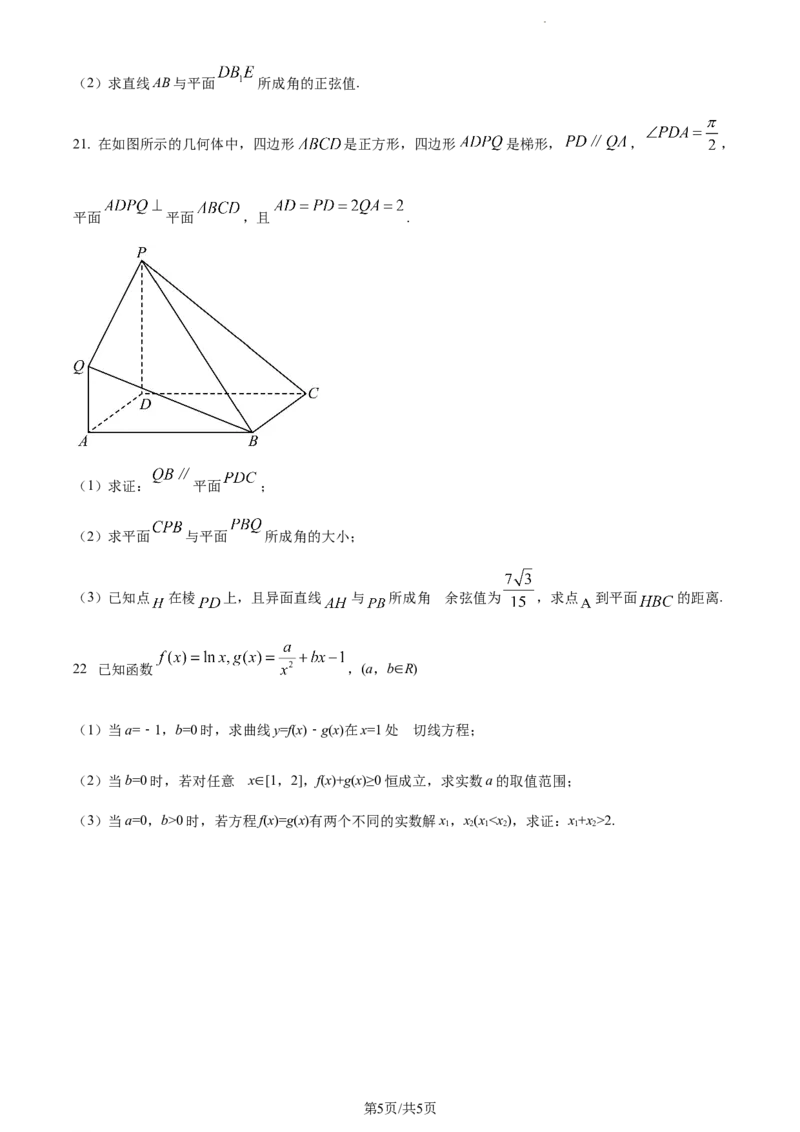
21. 在如图所示的几何体中,四边形 是正方形,四边形 是梯形, , ,
平面 平面 ,且 .
(1)求证: 平面 ;
(2)求平面 与平面 所成角的大小;
(3)已知点 在棱 上,且异面直线 与 所成角 的余弦值为 ,求点 到平面 的距离.
.
22 已知函数 ,(a,b∈R)
的
(1)当a=﹣1,b=0时,求曲线y=f(x)﹣g(x)在x=1处 切线方程;
的
(2)当b=0时,若对任意 x∈[1,2],f(x)+g(x)≥0恒成立,求实数a的取值范围;
(3)当a=0,b>0时,若方程f(x)=g(x)有两个不同的实数解x,x(x2.
1 2 1 2 1 2
第5页/共5页
学科网(北京)股份有限公司