文档内容
长春外国语学校2025-2026学年第一学期期中考试高二年级
数学试卷
出题人 :马竞 审题人:王先师
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共 2页。考试结束 A.2√(m+R)(n+R) B.√(m+R)(n+R) C.2√mn D.√mn
后,将答题卡交回。
注意事项:
.过点( , )的直线中,被圆 截得的弦长最大的直线方程是
1.答题前,考生先将自己的姓名、准考证号填写清楚,将条形码准确粘贴在考生信
息条形码粘贴区。 5 2 1
( )
2.选择题必须使用2B铅笔填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书写,
. . . .
字体工整、笔迹清楚。
3.请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效;在
A 3x-y-5=0 B 3x+y-7=0 C x+3y-5=0 D x+3y+5=0
.在下列等式中,使点 与点 一定共面的是( )
草稿纸、试题卷上答题无效。
4.作图可先使用铅笔画出,确定后必须用黑色字迹的签字笔描黑。
6
5.保持卡面清洁,不要折叠,不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。 . .
第I卷(选择题)
A B
一、单选题(本题共8小题,每题5分 ,共40分。在每小题列出的选项中,选出符合题 . .
目的一项) C D
.在空间直角坐标系中,点P , , 关于坐标平面xOy的对称点为( ) .已知 为椭圆 的焦点,P为椭圆上一动点, ,则 的
1 . , , . ,(1 ,2 -3) . , , . , , 7
最小值为( )
A (-1 -2 3) B (-1 -2 -3) C (-1 2 -3) D (1 2 3)
.过两点 的直线的倾斜角是 ,则 的值为( )
. . . .
2
. . . .
A B 1 C D
A 2 B C D 5
.在菱形 中若 是平面 的法向量则以下等式中可能不成立的是( )
.已知椭圆 的左右焦点分别是 , ,过 的直线与 相交
3 ABCD , ABCD ,
⃗PA⋅ ⃗AB=0 ⃗PC⋅⃗BD=0 ⃗PC⋅⃗AB=0 ⃗PA⋅C⃗D=0 8
. . . .
于A,B两点,若 , ,则 的离心率为( )
4.A我国发射的第一颗人B造地球卫星的运行轨道C是以地心(地球的中心D)F
2
为一个焦点
的椭圆.已知它的近地点(离地面最近的点)A距地面m千米,远地点(离地面最远
. . . .
的点)B距离地面n千米,并且F 、A、B在同一条直线上,地球的半径为R千米,
2
A B C D
则卫星运行的轨道的短轴长为( )千米 二、多选题(本题共3小题,每小题6分,共18分。在每小题给出的选项中,有多项符
合题目要求。全部选对的得6分,有选错的得0分。若只有2个正确选顶,每选对一个
得3分;若只有3个正确选项,每选对一个得2分。).已知平面 ,其中点 , ,则下列各点在平面内 ( 分)已知 且
9 15. 13
的是( ) 求实数 的值;
(1)
. . . . 若 ,求实数 的值.
A B C D (2)
.ΔABC
的三个顶点坐标为
A(4,0)
,
B(0,3), C(6,7)
,下列说法中正确的是( )
10
.边BC与直线 平行
A
.边BC上的高所在的直线的方程为
B
.过点A且平分ΔABC
面积的直线与边BC相交于点
D(3,5)
16.(15分)已知圆 : ,圆 : .
C
当 时,求圆 和圆 的公共弦长﹔
.过点C且在两坐标轴上的截距相等的直线方程一定是
(1)
D
是否存在实数a,使得圆 和圆 内含?若存在,求出实数a的取值范围,若不存
.已知直线 分别与 轴, 轴交于 , 两点,点 在圆 (2)
在,请说明理由.
11 AB
C:(x−1) 2 +(y+1) 2 =2 上,则ΔABP的面积可以是( )
. . . . 17.( 分)如图,在四棱锥 中,底面 为正方形, 平面 ,
A 7 B 8 C 9 D 15 ,E为 中点
第 Ⅱ 卷(非选择题)
三、填空题(本题共3小题,每小题5分,共15分) .
.经过A(0,2),B(1,0)两点的直线的方向向量为(1,k),则k的值是 .
12
⃗n
.已知直线l的方向向量 =(1,0,2),点A(0,1,1)在直线l上,则点P(1,2,2)
1到3直线l的距离为 .
.空间四边形 中, ,且异面直线 与 成 ,
14
求异面直线 与 所成角的余弦值为
求证: 平面 ;
四、解答题(本题共5小题,共77分。解答应写. 出文字说明,证明过程或演算步骤)
(1)求直线PC与平面 所成角的正弦值;
(2)求平面 与平面PAC夹角的余弦值 D B C A A C D B
9 10 11
(3) .
ABC BC BCD
18.( 分)在平面直角坐标系 中,已知圆 与 轴交于 ,
二.填空
17
12.-2 13. 14.
两点,圆 过 , 两点且与直线 相切.
/
三、解答题
( )求圆 的方程;
15.【答案】 ;
1
(1)2 (2) .
( )若直线 与圆 ,圆 的交点分别为点 , .求证:以线段 为直 【分析】( )根据空间向量平行的性质、空间向量线性运算公式进行求解即可;
2 ( )根据空1间向量垂直的坐标表示公式、空间向量线性运算公式即可求解
径的圆恒过点 .
2 .
【详解】( ) ,…………………… 分
1 ...1
, 设 ,…………………………………… 分
19.( 分)已知定圆 ,动圆N过点 且与圆M相切,记
2
17
动圆的圆心N的轨迹为E
, 的值为 .……… 分
求轨迹E的方程; .
2 5
(1)
已知两定点 和 ,过B的动直线 交轨迹E于P,Q两点若直线AP的斜
( )由( ) ,则 ,………… 分
(2) .
2 1 7
率为 ,直线AQ的斜率为 ,求证: 为定值 ,………………………… 分
. 9
,………… 分 .……… 分
长春外国语学校2025-2026学年第一学期期中考试高二年级 .11 13
16.【答案】 不存在,理由见解析
数学试卷答案
(1) (2)
【分析】( )两圆方程相减可得公共弦所在直线方程,再利用弦长公式求解;
一、 选择题
( )假设存1在实数a,根据两圆内含关系列不等式并求解,可判断a的存在性.
1 2 3 4 5 6 7 8 2
【详解】( )圆 : 即 ,…………… 分
1 1当 时,圆 : ,………………………… 分 又∵ , , 平面PAD,∴ 平面PAD,……… 分
2 2
又 平面PAD,∴ ,………………………………………………… 分
两圆方程相减可得公共弦所在直线方程为 ,…………… 分
∵ ,且E为 中点,∴ ,……………………… 分 3
3
圆 : 的圆心 ,半径 ,……………… 分 4
又 , 平面 ,
.5
∴ 平面 .…………………… 分
圆心 到公共弦所在直线的距离 ,…… 分
( )如图,以A为坐标原点,分别以A5B,AD,AP所在直线为x,y,z轴,
6
建2立空间直角坐标系,
则两圆的公共弦长为 ……………… 分
7
( )不存在,理由如下:
2
圆 : 可化为 ,
则圆心 ,半径 ,……………………………………… 分
9
又圆 : 的圆心 ,半径 ,…………… 分
则 , , , , ,P(0,0,2)
11
假设存在实数a,使得圆 和圆 内含,
⃗AC=(2,2,0),⃗AE=(0,1,1),⃗PC=(2,2,−2)
∴ ,………………… 分
则圆心距 ,……………………… 分
设平面 的法向量为 ,
6
13
即 ,此不等式无解,故不存在实数a,使得圆 和圆 内含…… 分
则 ,即 ,………………………… 分
.15
1 √6 7
17.【答案】 证明见解析
3 3
令 ,则 , ,∴ ,…………… 分
(1) (2) (3)
【分析】( )由线面垂直的判定定理可得 平面PAD,由线面垂直的性质定理得
8
2 1
,1进而利用线面垂直的判定定理得 平面 ; ∴cos< ⃗PC,⃗n>= = .
2√3×√3 3 分
( )以A为坐标原点,分别以AB,AD,AP所在直线为x,y,z轴,建立空间直角坐
………………………9
标2系,求出平面 的法向量、向量PC,由线面角公式可得答案.
sinθ=|cos< ⃗PC,⃗n>|=
1
PC 3
( )求出平面 的法向量、平面PAC的法向量,由向量的夹角公式可得答案.
设平面 与直线 所成的角为 ,则 ,
【3详解】( )∵ 平面 , 平面 ,∴ ,……… 分
1 11
所以平面 与直线PC所成角的正弦值为 .………………… 分 设圆 的方程为: ,圆心 坐标 , ,将 , 点代
3
10
( )∵ 平面 ,
BD⊂平面
,∴
PA⊥BD
………… 分
∵AC⊥BD,PA∩AC=A,PA,AC⊂平面PAC
3 11
入可得: ,解得: , ,……………………… 分
∴BD⊥平面PAC.∴平面PAC的法向量为⃗BD=(−2,2,0) 4
分
设平面 与平面PAC的夹角为α,则 …………13 由题意可得 ,所以 ,可得 ,……………… 分
4 √6 6
cosα=|cos< ⃗BD,⃗n>|= = ,
2√2×√3 3
所以圆 的方程为: ;……………………… 分
√6 8
所以平面 与平面PAC的夹角余弦值为 …………………… 分
3 ( )由题意可得 且 ,………………… 分
15
18.【答案】( ) ﹣ ﹣ ;( )证明见解析 2 9
2 2
1x y+ x2 y4 =0 2 . 联立与圆 的方程: ,整理得: ,可得
【分析】( )由圆 的方程求出 轴上的点 , 的坐标,设圆 的一般方程求出圆
1
心 坐标,由题意过 , 点代入圆的方程求出参数的值,又有与直线 相切,即 , ,………………………………… 分
11
联立与圆 的方程: ,整理得: ,可得
可得参数的值,进而求出圆 的方程;
( )由题意将直线 分别于两个圆联立求出 , 的坐标,注意不能相切,即 的值
, ,……………………………… 分
2
13
满足 且 ,进而求出直线 , 的斜率,可得两条直线的斜率为定值 ,
因为 , ,………………… 分
可得直线垂直,即可证明线段 为直径的圆恒过点 .
15
【详解】解:( )由题意令 ,代入圆 中可得 , ,可得: ,
,即 ,
1
所以以线段 为直径的圆恒过点 .…………………………… 分
,……………………………… 分
17
19.【答案】 证明见解析
..2
(1) (2)
【分析】( )结合椭圆定义,用定义法求轨迹E的方程即可;
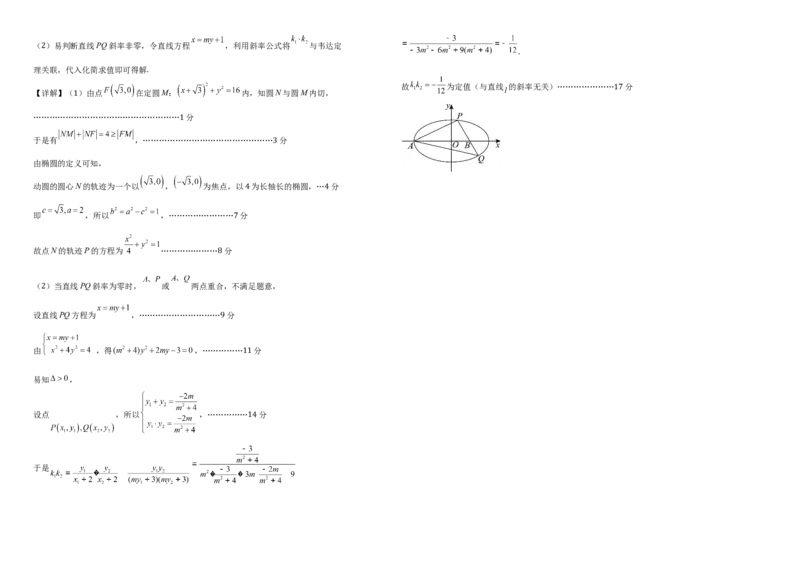
1( )易判断直线PQ斜率非零,令直线方程 ,利用斜率公式将 与韦达定
2
理关联,代入化简求值即可得解 .
. 故 为定值(与直线 的斜率无关)………………… 分
【详解】( )由点 在定圆M: 内,知圆N与圆M内切,
17
1
……………………………………………… 分
1
于是有 ,………………………………………… 分
3
由椭圆的定义可知,
动圆的圆心N的轨迹为一个以 , 为焦点,以 为长轴长的椭圆,… 分
4 4
即 ,所以 ,…………………… 分
7
故点N的轨迹P的方程为 ………………… 分
8
( )当直线PQ斜率为零时, 或 两点重合,不满足题意,
2
设直线PQ方程为 ,………………………… 分
9
由 ,得 ,…………… 分
11
易知 ,
设点 ,所以 ,…………… 分
14
于是