2004年云南高考文科数学真题及答案(1)_数学高考真题试卷_旧1990-2007·高考数学真题_1990-2007·高考数学真题·PDF_云南

2004 年云南高考文科数学真题及答案 本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。第Ⅰ卷1至2页，第Ⅱ卷3至10页。考试 结束后，将本试卷和答题卡一并交回。 第I卷 参考公式： 正棱台、圆台的侧面积公式 三角函数的和差化积公式 1 S  (cc)l 台侧 2 1 sincos [sin()sin()] 其中c′、c分别表示上、下底面周长，l表示 2 斜高或母线长 1 cossin [sin()sin()] 台体的体积公式 2 4 1 V  R3 coscos [cos()cos()] 球 3 2 其中R表示球的半径 1 sinsin [cos()cos()] 2 一、选择题 （1）设集合M  x,y x2  y2 1,xR,yR  ，N  x,y x2  y 0,xR,yR  ， 则集合M N中元素的个数为（ ）  A．1 B．2 C．3 D．4 x （2）函数y  sin 的最小正周期是（ ） 2  A． B． C．2 D．4 2 (3) 记函数y 13x的反函数为y  g(x)，则g(10)（ ） A． 2 B． 2 C． 3 D． 1 (4) 等比数列a 中，a 9, a 243，则a 的前4项和为（ ） n 2 5 n A． 81 B． 120 C．168 D． 192   (5) 圆x2  y2 4x0在点P 1, 3 处的切线方程是（ ） A． x 3y20 B． x 3y40 C． x 3y40 D． x 3y20 第1页 | 共11页6  1 (6)  x   展开式中的常数项为（ ）  x A． 15 B． 15 C． 20 D． 20 2 (7) 设复数z的幅角的主值为 ，虚部为 3，则z2 （ ） 3 A． 22 3i B． 2 32i C． 22 3i D． 2 32i 1 (8) 设双曲线的焦点在x轴上，两条渐近线为y  x，则双曲线的离心率e（ ） 2 5 5 A． 5 B． 5 C． D． 2 4 (9) 不等式1 x1 3的解集为（ ） A． 0,2 B． 2,0 2,4  C． 4,0 D． 4,2 0,2  (10) 正三棱锥的底面边长为2，侧面均为直角三角形，则此三棱锥的体积为（ ） 2 2 4 A． 2 B． 2 C． D． 2 3 3 3 (11) 在 ABC中，AB3,BC  13,AC 4，则边AC上的高为（ ）  2 2 3 A． 2 B． 3 C． D．3 3 3 3 2 (12) 4名教师分配到3所中学任教，每所中学至少1名教师，则不同的分配方案共有（ ） A． 12 种 B． 24 种 C 36 种 D． 48 种 第Ⅱ卷 二、填空题：本大题共4小题，每小题4分，共16分. 把答案填在题中横线上. (13) 函数y  log (x1) 的定义域是 . 1 2 R (14) 用平面α截半径为R的球，如果球心到平面α的距离为 ，那么截得小圆的面积与球 2 的表面积的比值为 . 第2页 | 共11页1 (15) 函数y sinx cosx(xR)的最大值为 . 2 (16) 设P为圆x2  y2 1上的动点，则点P到直线3x4y100的距离的最小值为 . 三、解答题：本大题共6小题，共74分. 解答应写出文字说明，证明过程或演算步骤. (17)（本小题满分12分） 解方程4x 2x2 120. (18) （本小题满分12分） 1 sin2cossin 已知α为锐角，且tan ,求 的值. 2 sin2cos2 第3页 | 共11页(19) （本上题满分12分） 设数列{a }是公差不为零的等差数列，S 是数列{a }的前n项和，且S2 9S , n n n 1 2 S  4S ，求数列{a }的通项公式. 4 2 n 第4页 | 共11页20．（本小题满分12分） 某村计划建造一个室内面积为800m2的矩形蔬菜温室，在温室内，沿左、右两侧与后侧 内墙各保留1m宽的通道，沿前侧内墙保留3m宽的空地。当矩形温室的边长各为多少 时，蔬菜的种植面积最大？最大种植面积是多少？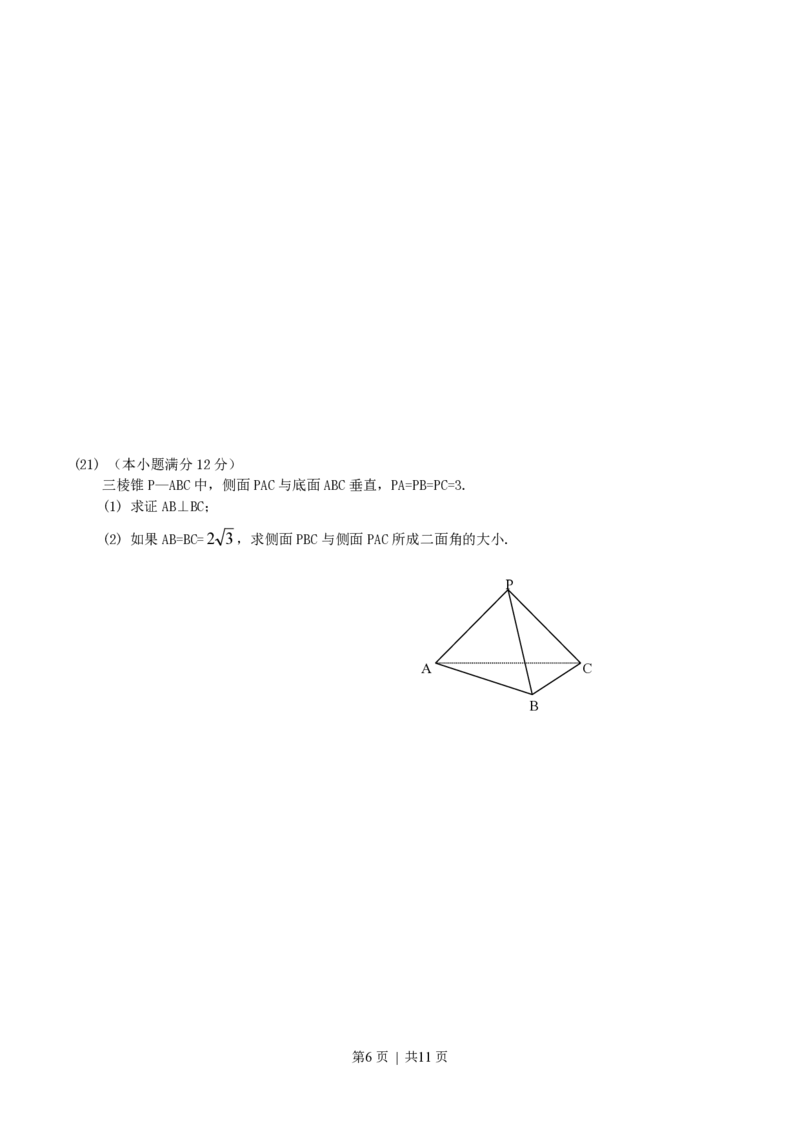 第5页 | 共11页(21) （本小题满分12分） 三棱锥P—ABC中，侧面PAC与底面ABC垂直，PA=PB=PC=3. (1) 求证AB⊥BC； (2) 如果AB=BC=2 3，求侧面PBC与侧面PAC所成二面角的大小. P A C B 第6页 | 共11页(22)（本小题满分14分） x2 设椭圆  y2 1的两个焦点是F (c,0)与F (c,0)(c 0)，且椭圆上存在点P， m1 1 2 使得直线PF 与直线PF 垂直. 2 2 （1）求实数m的取值范围； |QF | （2）设L是相应于焦点F 的准线，直线PF 与L相交于点Q. 若 2  2 3， 2 2 | PF | 2 求直线PF 的方程. 2 第7页 | 共11页2004年普通高等学校招生全国统一考试 数学（文史类）（老课程）参考答案 1—12 BCBBD AACDC BC 3 5 13．{x|1 x  2} 14． 15． 16．1 16 2 三、解答题 17．本小题主要考查指数和对数的性质以及解方程的有关知识. 满分12分. 解：(2x)2 4(2x)12 0. (2x 6)(2x 2) 0. 2x 6.2x  2（无解）. 所以x log 6. 2 18．本小题主要考查同角三角函数的基本关系式、二倍角公式等基础知识以及三角恒等变形 的能力. 满分12分. sincos2 解：原式 . 2sincoscos2 1 因为 tan 时,sin 0,cos2 0, 2 1 所以 原式 . 2cos 1 2 因为为锐角，由tan ,得cos . 2 5 5 所以 原式 . 4 1 2 因为为锐角，由tan 得cos . 2 5 5 所以 原式 . 4 第8页 | 共11页19．本小题主要考查等差数列的通项公式，前n项和公式等基础知识，根据已知条件列方程 以及运算能力.满分12分. n(n1) 解：设等差数列{a }的公差为d，由S  na  d及已知条件得 n n 1 2 (3a 3d)2 9(2a d)， ① 1 1 4a 6d  4(2a d), ② 1 1 4 由②得d  2a ，代入①有a2  a 1 1 9 1 4 解得 a 0或a  . 当a 0时,d 0,舍去. 1 1 9 1 4 8 因此 a  ,d  . 1 9 9 4 8 4 故数列{a }的通项公式a  (n1)  (2n1). n n 9 9 9 20．本小题主要考查把实际问题抽象为数学问题，应用不等式等基础知识和方法解决问题的 能力. 满分12分. 解：设矩形温室的左侧边长为a m，后侧边长为b m，则 ab 800. 蔬菜的种植面积 S (a4)(b2)  ab4b2a8 8082(a2b). 所以S 8084 2ab 648(m2). 当a2b,即a40(m),b  20(m)时,S 648(m2). 最大值 答：当矩形温室的左侧边长为40m，后侧边长为20m时，蔬菜的种植面积最大，最 大种植面积为648m2. 21．本小题主要考查两个平面垂直的性质、二面角等有关知识，以有逻辑思维能力和空间想 象能力. 满分12分. P （1）证明：如果，取AC中点D，连结PD、BD. E 因为PA=PC，所以PD⊥AC， 又已知面PAC⊥面ABC， 所以PD⊥面ABC，D为垂足. A D C 因为PA=PB=PC， 所以DA=DB=DC，可知AC为△ABC外接圆直径， B 因此AB⊥BC. （2）解：因为AB=BC，D为AC中点，所以BD⊥AC. 又面PAC⊥面ABC， 所以BD⊥平面PAC，D为垂足. 第9页 | 共11页作BE⊥PC于E，连结DE， 因为DE为BE在平面PAC内的射影， 所以DE⊥PC，∠BED为所求二面角的平面角. 在Rt△ABC中，AB=BC=2 3，所以BD= 6 . 在Rt△PDC中，PC=3，DC= 6 ，PD= 3， PDDC 3 6 所以DE    2. PC 3 6 因此，在Rt△BDE中，tanBED   3， 2 BED 60， 所以侧面PBC与侧面PAC所成的二面角为60°. 22．本小题主要考查直线和椭圆的基本知识，以及综合分析和解题能力. 满分14分. 解：（1）由题设有m 0,c  m. y y 设点P的坐标为（x ,y ），由PF  PF ，得 0  0  1， 0 0 1 2 x c x c 0 0 化简得 x2  y2  m. ① 0 0 x2 m2 1 1 将①与 0  y2 1联立，解得 x2  ,y2  . m1 0 0 m 0 m m2 1 由m 0,x2  0,得m1. 0 m 所以m的取值范围是m1. m1 m1 （2）准线L的方程为x  .设点Q的坐标为(x ,y )，则x  . 1 1 1 m m m1  m |QF | x c m 2  1  . ② | PF | cx m x 2 0 0 m2 1 |QF | 1 将x  代入②，化简得 2   m m2 1. 0 m | PF | m m2 1 2 |QF | 由题设 2  2 3，得 m m2 1  2 3，无解. | PF | 2 第10页 | 共11页m2 1 将x   代入②，化简得 0 m |QF | 1 2   m m2 1. | PF | m m2 1 2 |QF | 由题设 2  2 3，得 m m2 1  2 3. | PF | 2 解得m=2. 3 2 从而x   ,y   ,c  2,得到PF 的方程 0 2 0 2 2 y  ( 32)(x 2). 第11页 | 共11页