文档内容
济宁市实验中学 2025 届高三第一学期 10 月月考数学试题
一、单选题
1. 已知集合
或x>2},
,若 ,则实数 的取值范围是( )
A. B. C. D.
2. “ 或 ”是“幂函数 在 上是减函数”的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
3. 函数 ,若对任意 ,都有 成立,
则实数 的取值范围为( )
A. B.
C. D.
4. 已知 ,则 ( )
.
A B. C. D.
5. 函数y=lg 的大致图象为( )
A. B. C. D..
6 当 时,函数 取得最大值 ,则 ( )
A. B. C. D. 1
7. 已知函数 ,则使 有零点的一个充分条件是( )
A. B. C. D.
8. 已知函数 , , , ,则( )
A. B. C. D.
二、多选题
9. 设函数 ,则( )
A. 当 时, 有三个零点
的
B. 当 时, 是 极大值点
C. 存在a,b,使得 为曲线 的对称轴
D. 存在a,使得点 为曲线 的对称中心
10. 若正实数a,b满足 ,则下列说法错误的是( )
A. 有最小值 B. 有最大值
C. 有最小值4 D. 有最小值11. 函数 ,关于x的方程 ,则下列正确的是( )
A. 函数 的值域为R
B. 函数 的单调减区间为
C. 当 时,则方程有4个不相等的实数根
D. 若方程有3个不相等的实数根,则m的取值范围是
三、填空题
12. 设正实数 满足 ,则 __________.
13. 已知函数 的定义域为 ,且 为奇函数, 为偶函数, ,则
__________.
14. 已知函数 若存在实数 满足 ,且 ,则 的
取值范围为__________.
四、解答题
15. 函数 的定义域为集合A,函数 的值域为集合B.
(Ⅰ)求集合A,B;
(Ⅱ)若集合A,B满足 ,求实数a的取值范围.
16. 已知 ,(1)求 和 的值
(2)若 , ,求 大的小.
17. 已知函数 .
(1)当 时,求曲线 在点 处的切线方程;
(2)若 有极小值,且极小值小于0,求a的取值范围.
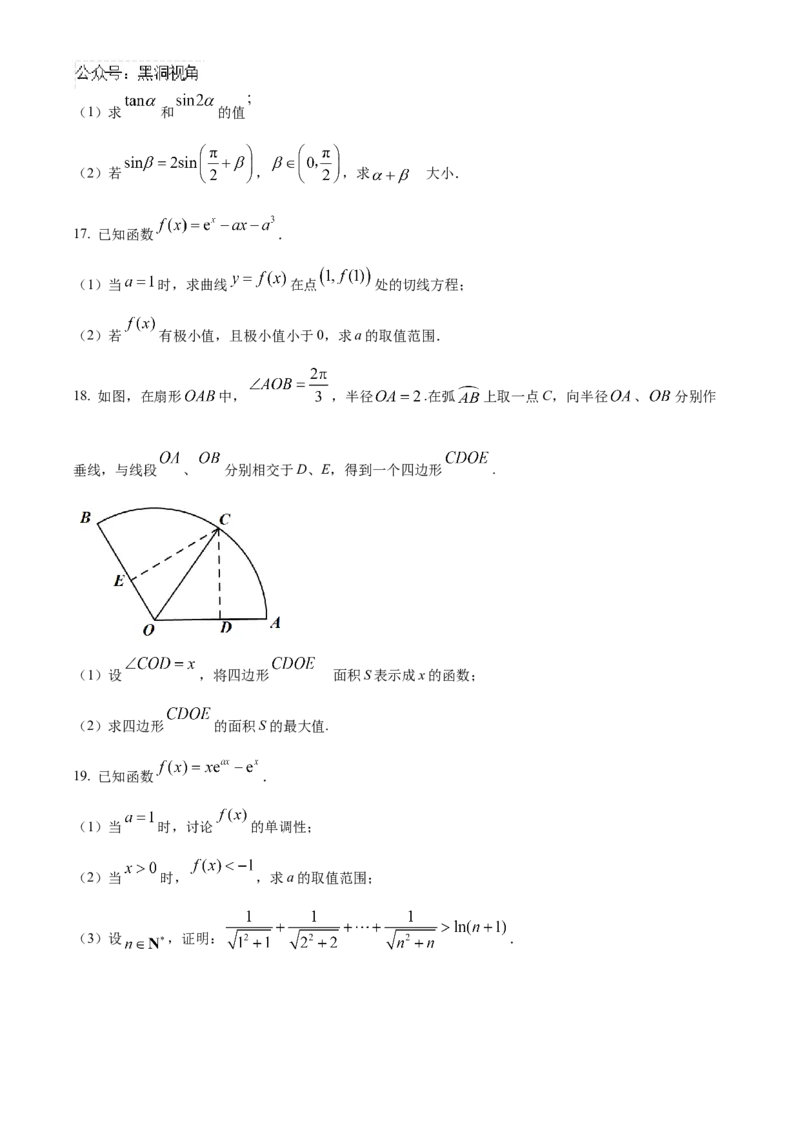
18. 如图,在扇形 中, ,半径 .在弧 上取一点C,向半径 、 分别作
垂线,与线段 、 分别相交于D、E,得到一个四边形 .
的
(1)设 ,将四边形 面积S表示成x的函数;
(2)求四边形 的面积S的最大值.
19. 已知函数 .
(1)当 时,讨论 的单调性;
(2)当 时, ,求a的取值范围;
(3)设 ,证明: .