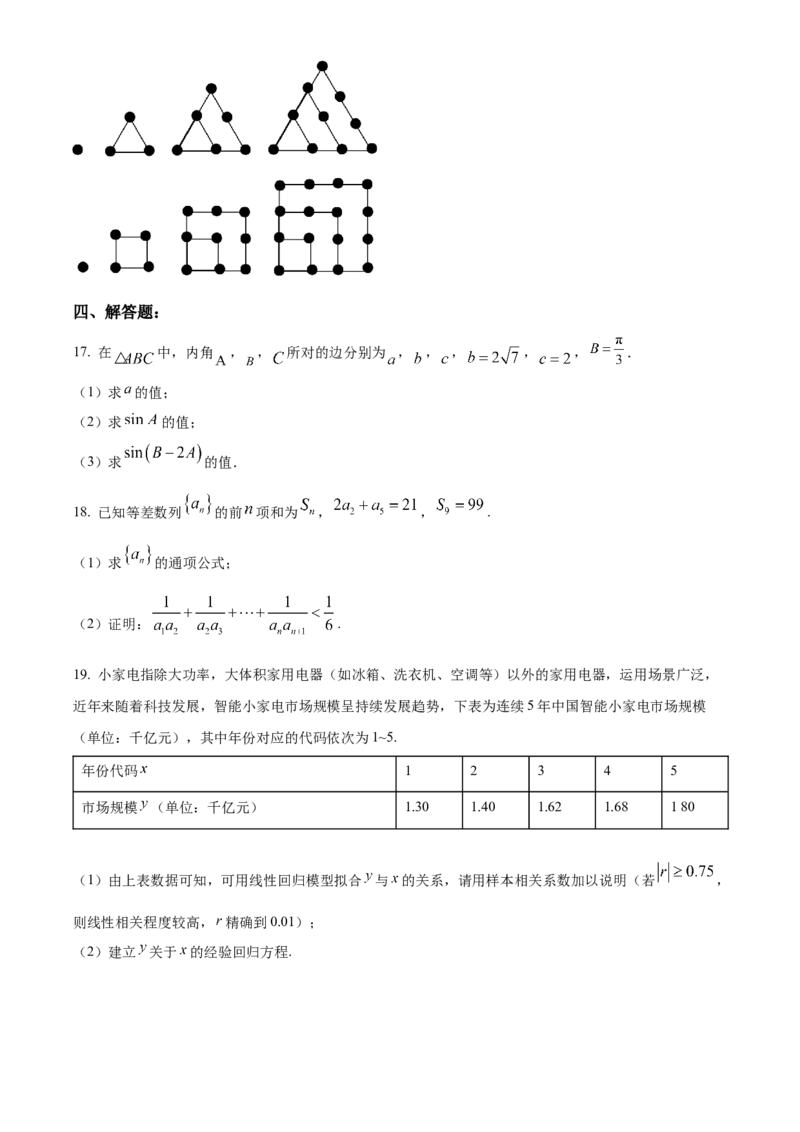文档内容
东莞四中 2023-2024 高三第一学期数学月考试题与答案
一、单项选择题:
1. 已知集合 , ,则 ( )
A. B. C. D.
2. 已知 , 是实数,则“ ”是“ ”的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
3. 下列函数既是偶函数,又在 上单调递增的是( )
A. B.
.
C D.
4. 在 的展开式中, 的系数是( )
A. B. 8 C. D. 4
5. 《九章算术》“竹九节”问题:现有一根9节的竹子,自上而下各节的容积成等差数列,上面4节的容积
共3升,下面3节的容积共4升,则第5节的容积为( )
A. 升 B. 升 C. 升 D. 升
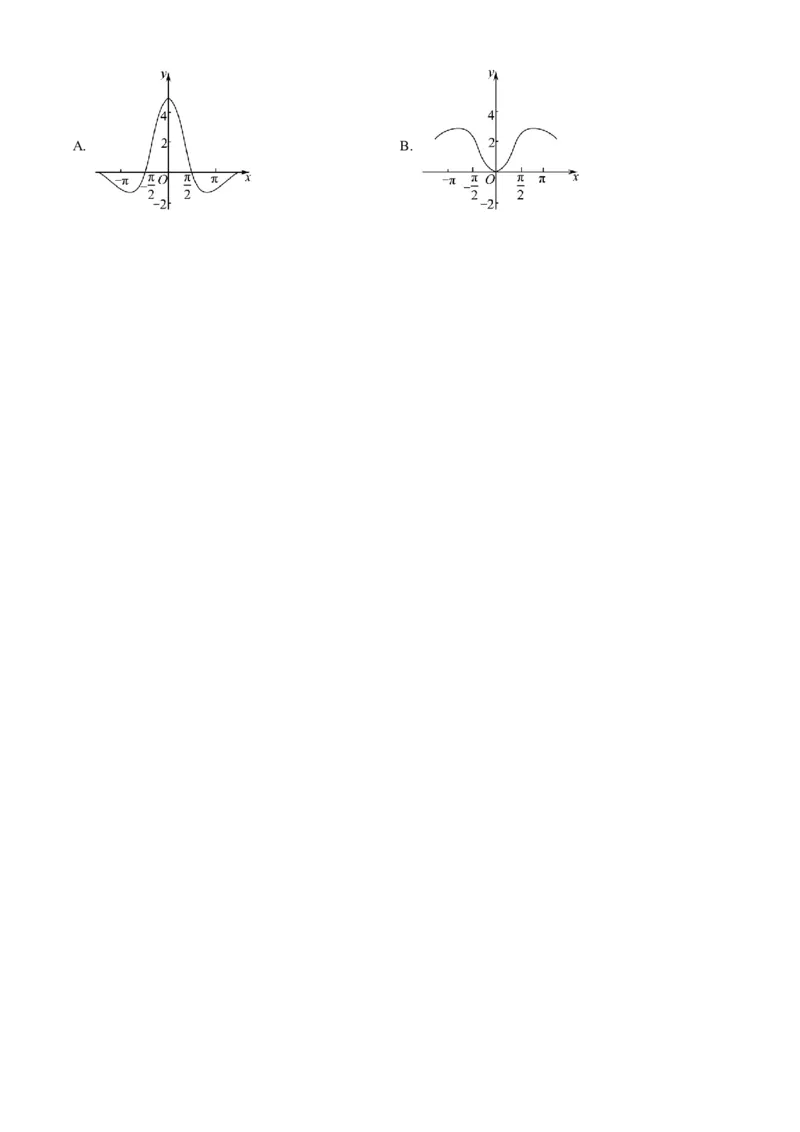
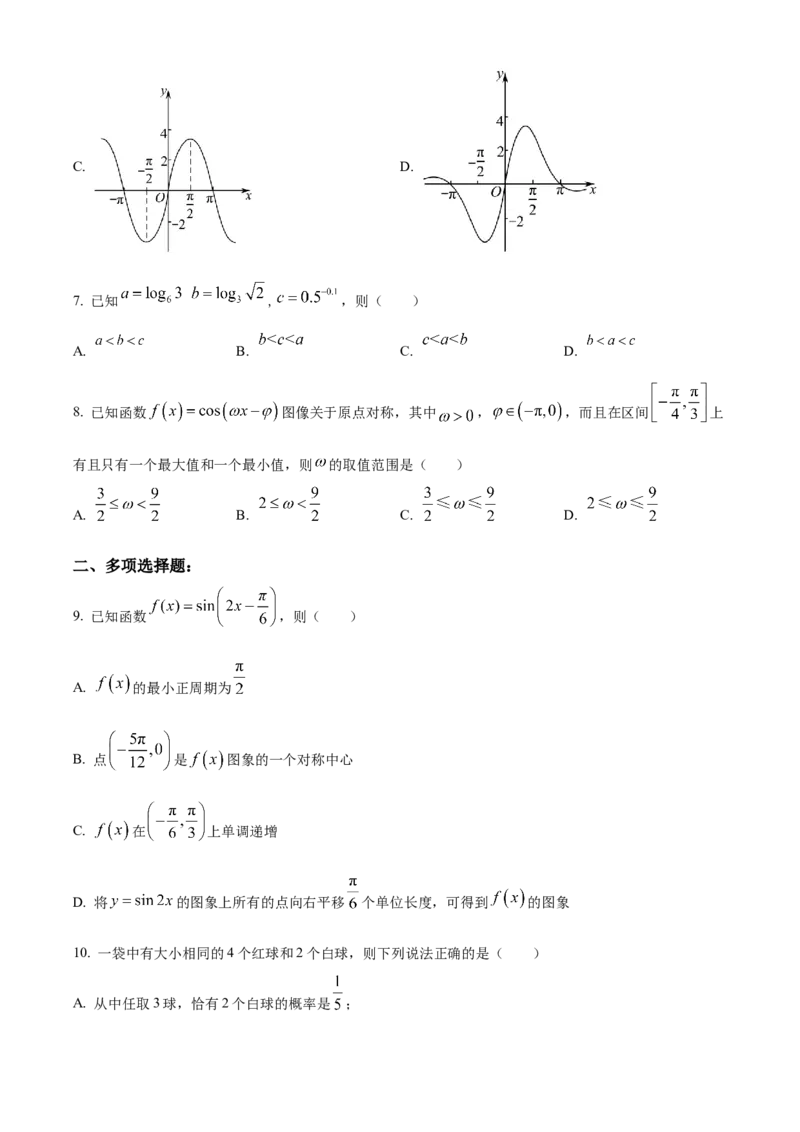
6. 函数 的大致图象为( )A. B.C. D.
,
7. 已知 , ,则( )
A. B. C. D.
8. 已知函数 图像关于原点对称,其中 , ,而且在区间 上
有且只有一个最大值和一个最小值,则 的取值范围是( )
A. B. C. D.
二、多项选择题:
9. 已知函数 ,则( )
A. 的最小正周期为
B. 点 是 图象的一个对称中心
C. 在 上单调递增
D. 将 的图象上所有的点向右平移 个单位长度,可得到 的图象
10. 一袋中有大小相同的4个红球和2个白球,则下列说法正确的是( )
A. 从中任取3球,恰有2个白球的概率是 ;B. 从中有放回的取球6次,每次任取一球,设取到红球次数为X,则 ;
C. 现从中不放回的取球2次,每次任取1球,则在第一次取到红球后,第二次再次取到红球的概率为 ;
D. 从中有放回的取球3次,每次任取一球,则至少有一次取到白球的概率为 .11. 已知函数 存在极值点,则实数a的值可以是( )
A. 0 B. C. D.
12. 生态学研究发现:当种群数量较少时,种群近似呈指数增长,而当种群增加到一定数量后,增长率就
会随种群数量的增加而逐渐减小,为了刻画这种现象,生态学上提出了著名的逻辑斯谛模型:
,其中 , , 是正数, 表示初始时刻种群数量, 叫做种群的内秉增
长率, 是环境容纳量. 可以近似刻画 时刻的种群数量.下面给出四条关于函数 的判断正确的
有( )
A. 如果 ,那么存在 , ;
B. 如果 ,那么对任意 , ;
C. 如果 ,那么存在 , 在 点处的导数 ;
D. 如果 ,那么 的导函数 在 上存在最大值.
三、填空题:
13. 在 中, , , ,则 ______.
14. 某中学为庆祝建校130周年,高二年级派出甲、乙、丙、丁、戊5名老师参加“130周年办学成果展”活动,
活动结束后5名老师排成一排合影留念,要求甲、乙两人不相邻且丙、丁两人必须相邻,则排法共有
__________种(用数字作答).
15. 已知角 的大小如图所示,则 的值为________16. 古希腊毕达哥拉斯学派的数学家用沙粒和小石子来研究数,他们根据沙粒或小石子所排列的形状,把
数分成许多类,如图,第一行图形中黑色小点个数:1,3,6,10,…称为三角形数,第二行图形中黑色
小点个数:1,4,9,16,…称为正方形数,记三角形数构成数列 ,正方形数构成数列 ,则
______; ______.四、解答题:
17. 在 中,内角 , , 所对的边分别为 , , , , , .
(1)求 的值;
(2)求 的值;
(3)求 的值.
18. 已知等差数列 的前 项和为 , , .
(1)求 的通项公式;
(2)证明: .
19. 小家电指除大功率,大体积家用电器(如冰箱、洗衣机、空调等)以外的家用电器,运用场景广泛,
近年来随着科技发展,智能小家电市场规模呈持续发展趋势,下表为连续5年中国智能小家电市场规模
(单位:千亿元),其中年份对应的代码依次为1~5.
年份代码 1 2 3 4 5
.
市场规模 (单位:千亿元) 1.30 1.40 1.62 1.68 180
(1)由上表数据可知,可用线性回归模型拟合 与 的关系,请用样本相关系数加以说明(若 ,
则线性相关程度较高, 精确到0.01);
(2)建立 关于 的经验回归方程.参考公式和数据:样本相关系数 , ,
, , , .
20. 设正项数列 的前 项和为 ,且 .
(1)求数列 的通项公式;
(2)记 的前 项和为 ,求证: .
21. 哈六中举行数学竞赛,竞赛分为初赛和决赛两阶段进行.初赛采用“两轮制”方式进行,要求每个学年派
出两名同学,且每名同学都要参加两轮比赛,两轮比赛都通过的同学才具备参与决赛的资格.高三学年派出
甲和乙参赛.在初赛中,若甲通过第一轮与第二轮比赛的概率分别是 , ,乙通过第一轮与第二轮比赛的
概率分别是 , ,且每名同学所有轮次比赛的结果互不影响.
(1)若高三学年获得决赛资格的同学个数为 ,求 的分布列和数学期望.
的
(2)已知甲和乙都获得了决赛资格.决赛 规则如下:将问题放入 两个纸箱中, 箱中有3道选择题
和2道填空题, 箱中有3道选择题和3道填空题.决赛中要求每位参赛同学在 两个纸箱中随机抽取两
题作答.甲先从 箱中依次抽取2道题目,答题结束后将题目一起放入 箱中,然后乙再抽取题目.已知乙
从 箱中抽取的第一题是选择题,求甲从 箱中抽出的是2道选择题的概率.
22. 已知函数 ,其中 为常数.
(1)当 时,判断 在区间 内的单调性;(2)若对任意 ,都有 ,求 的取值范围.