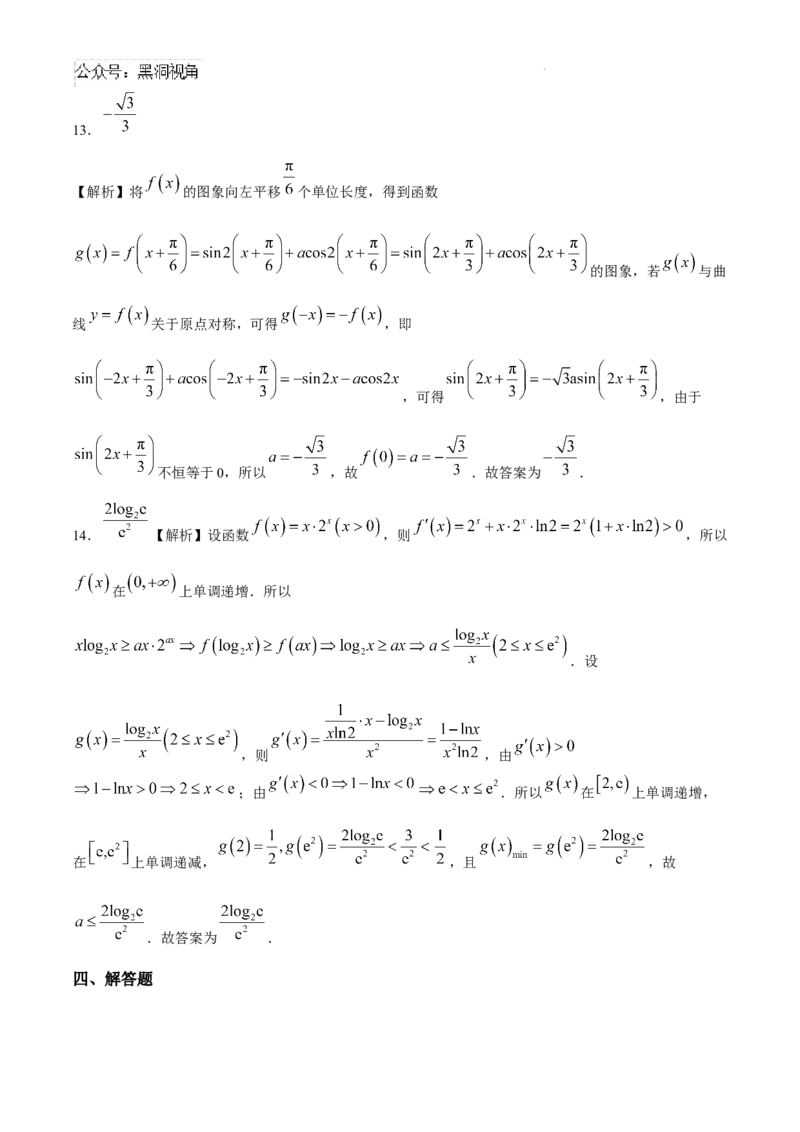文档内容
菏泽市 2024—2025 学年度第一学期期中考试
高三数学试题
本试卷共4页,19题。全卷满分150分。考试用时120分钟。
注意事项:
1.答题前,先将自己的姓名、准考证号填写在答题卡上,并将准考证号条形码粘贴在答题卡
上的指定位置。
2.选择题的作答:每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。写
在试题卷、草稿纸和答题卡上的非答题区域均无效。
3.非选择题的作答:用签字笔直接写在答题卡上对应的答题区域内。写在试题卷、草稿纸和
答题卡上的非答题区域均无效。
4.考试结束后,请将本试题卷和答题卡一并上交。
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项
是符合题目要求的.
1.已知集合 ,则 ( )
A. B. C. D.
2.已知函数 的定义域为 ,则函数 的定义域为( )
A. B. C. D.
3.已知 ,则 ( )
A. B. C.0 D.1
4.“函数 在 上单调递增”是“ ”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分又不必要条件
5.过曲线 上一点 作平行于两坐标轴的直线,分别交曲线 于点 ,若直线 过
原点,则其斜率为( )
A.1 B. C. D.
学科网(北京)股份有限公司6.函数 的零点个数为( )
A.1 B.0 C.3 D.2
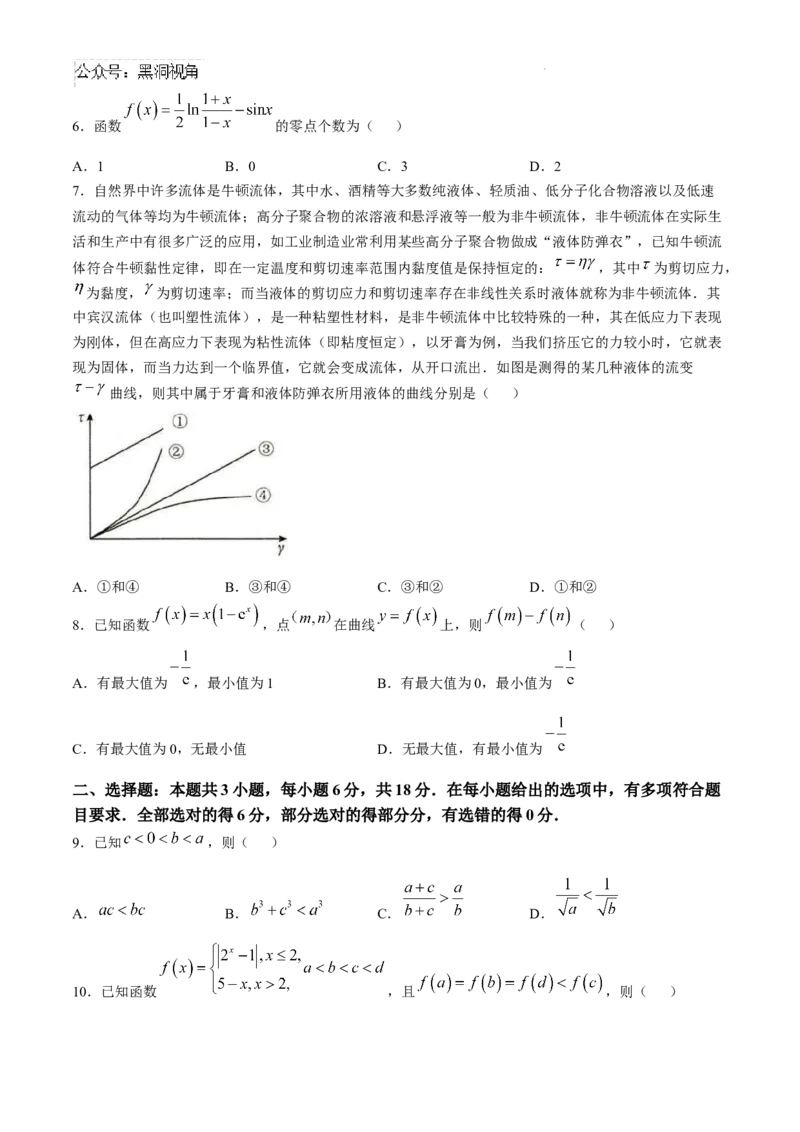
7.自然界中许多流体是牛顿流体,其中水、酒精等大多数纯液体、轻质油、低分子化合物溶液以及低速
流动的气体等均为牛顿流体;高分子聚合物的浓溶液和悬浮液等一般为非牛顿流体,非牛顿流体在实际生
活和生产中有很多广泛的应用,如工业制造业常利用某些高分子聚合物做成“液体防弹衣”,已知牛顿流
体符合牛顿黏性定律,即在一定温度和剪切速率范围内黏度值是保持恒定的: ,其中 为剪切应力,
为黏度, 为剪切速率;而当液体的剪切应力和剪切速率存在非线性关系时液体就称为非牛顿流体.其
中宾汉流体(也叫塑性流体),是一种粘塑性材料,是非牛顿流体中比较特殊的一种,其在低应力下表现
为刚体,但在高应力下表现为粘性流体(即粘度恒定),以牙膏为例,当我们挤压它的力较小时,它就表
现为固体,而当力达到一个临界值,它就会变成流体,从开口流出.如图是测得的某几种液体的流变
曲线,则其中属于牙膏和液体防弹衣所用液体的曲线分别是( )
A.①和④ B.③和④ C.③和② D.①和②
8.已知函数 ,点 在曲线 上,则 ( )
A.有最大值为 ,最小值为1 B.有最大值为0,最小值为
C.有最大值为0,无最小值 D.无最大值,有最小值为
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题
目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.已知 ,则( )
A. B. C. D.
10.已知函数 ,且 ,则( )
学科网(北京)股份有限公司A. B. C. D.
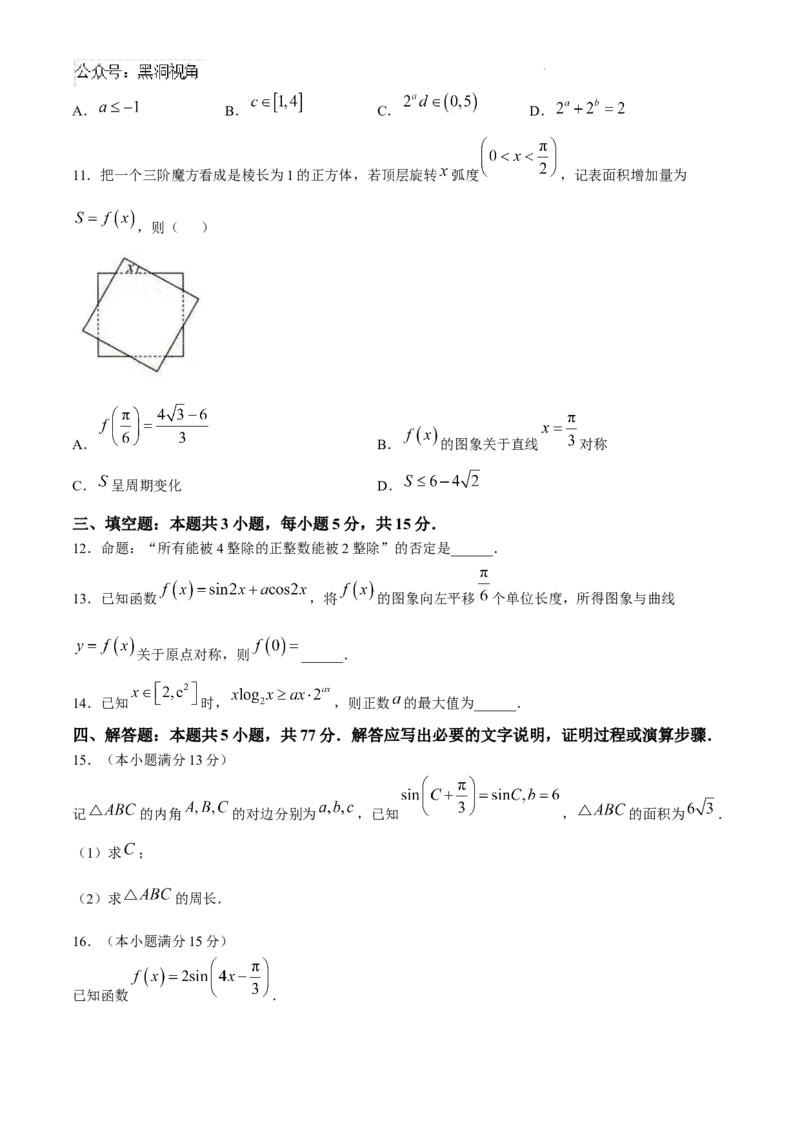
11.把一个三阶魔方看成是棱长为1的正方体,若顶层旋转 弧度 ,记表面积增加量为
,则( )
A. B. 的图象关于直线 对称
C. 呈周期变化 D.
三、填空题:本题共3小题,每小题5分,共15分.
12.命题:“所有能被4整除的正整数能被2整除”的否定是______.
13.已知函数 ,将 的图象向左平移 个单位长度,所得图象与曲线
关于原点对称,则 ______.
14.已知 时, ,则正数 的最大值为______.
四、解答题:本题共5小题,共77分.解答应写出必要的文字说明,证明过程或演算步骤.
15.(本小题满分13分)
记 的内角 的对边分别为 ,已知 , 的面积为 .
(1)求 ;
(2)求 的周长.
16.(本小题满分15分)
已知函数 .
学科网(北京)股份有限公司(1)求 的单调递减区间;
(2)若 ,求 的最大值.
17.(本小题满分15分)
记锐角 的内角 的对边分别为 ,已知 .
(1)求 ;
(2)延长 到 ,使 ,求 .
18.(本小题满分17分)
已知函数 .
(1)求 的单调区间;
(2)设 分别为 的极大值点和极小值点,记 .证明:直线 与曲
线 交于另一点 .
19.(本小题满分17分)
已知函数 ,其中 ,
(1)证明: ;
(2)探究 是否有最小值,如果有,请求出来;如果没有,请说明理由.
菏泽市 2024—2025 学年度第一学期期中考试
高三数学参考答案及解析
一、选择题
1.B【解析】 时,不等式 的解集为 ,即 ,不等式 ,解得
,即 ,故 .故选B.
2.B【解析】因为函数 的定义域为 ,即 ,所以 ,由 解
学科网(北京)股份有限公司得 ,所以函数 的定义域为 .故选B.
3.A【解析】由诱导公式可得 ,故 .
故选A.
4.A【解析】 在 上单调递增,则 ,即 在 上
恒成立,则必有 ,所以“函数 在 上单调递增”是“ ”的充分不必要条
件.故选A.
5.B【解析】设 ,则 , ,由题意可得 ,
解得 或 ,经检验, 不符合,故其斜率为 .故选B.
6.A【解析】由 ,可得 ,即定义域为 ,所以 ,即
在 上为单调递增函数,又 ,所以 仅有一个零点.故选A.
7.D【解析】由题意得牛顿流体黏度 恒定,即在 曲线中,图象为直线,即③为牛顿流体,④和②
为非牛顿流体,由题意可知牙膏是特殊的非牛顿流体,但挤压力达到一定值时变成流体其粘度不变,即此
时剪切应力与剪切速率成线性关系,故牙膏所对应的曲线为①,而液体防弹衣所用液体本身属于非牛顿流
体,且根据题意表述可知剪切应力随剪切速率的增大而增大且比正常条件下的牛顿流体所对应的剪切应力
大,故液体防弹衣所用液体对应曲线为2.故选D.
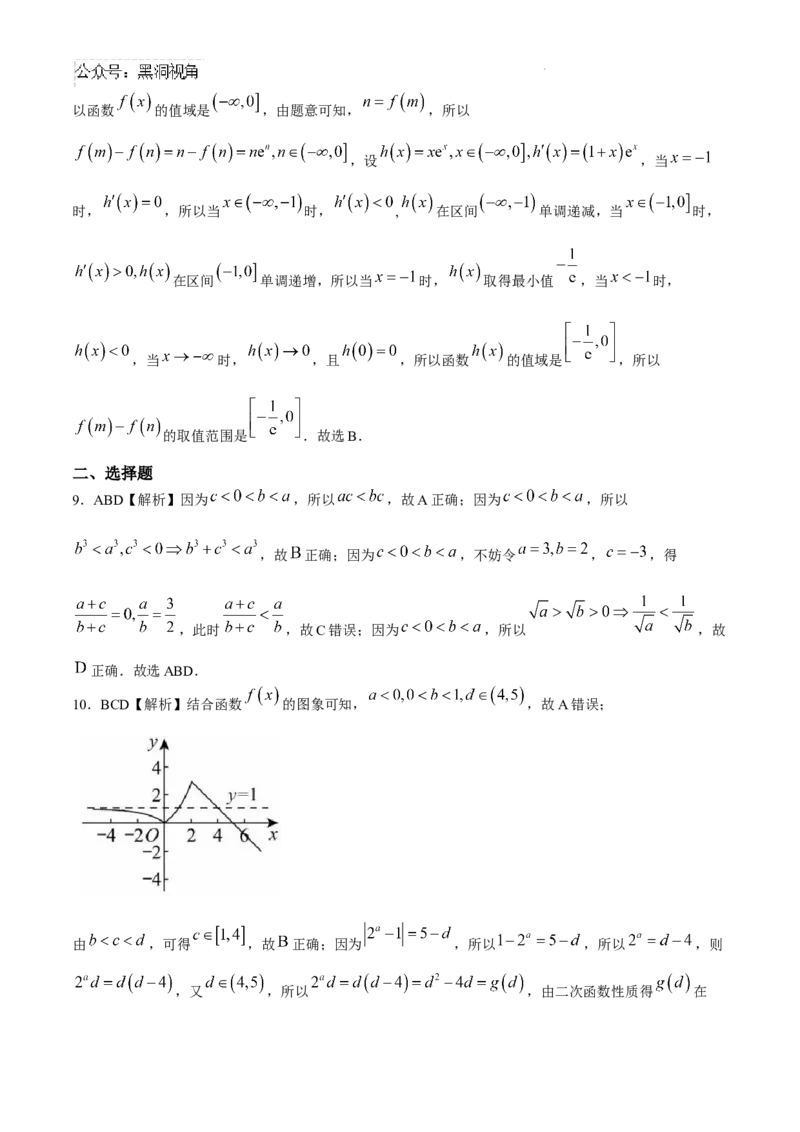
8.B【解析】 ,设 ,当 时,
在区间 单调递增,当 时, 在区间 单调递减,
所以当 时, 取得最大值, ,且 时, , ,所以
当 时, ,即 ,函数 在区间 上单调递增,当 时, ,
即 ,函数 在区间 上单调递减,所以当 时, 取得最大值 ,所
学科网(北京)股份有限公司以函数 的值域是 ,由题意可知, ,所以
,设 ,当
时, ,所以当 时, , 在区间 单调递减,当 时,
在区间 单调递增,所以当 时, 取得最小值 ,当 时,
,当 时, ,且 ,所以函数 的值域是 ,所以
的取值范围是 .故选B.
二、选择题
9.ABD【解析】因为 ,所以 ,故A正确;因为 ,所以
,故 正确;因为 ,不妨令 , ,得
,此时 ,故C错误;因为 ,所以 ,故
正确.故选ABD.
10.BCD【解析】结合函数 的图象可知, ,故A错误;
由 ,可得 ,故 正确;因为 ,所以 ,所以 ,则
,又 ,所以 ,由二次函数性质得 在
学科网(北京)股份有限公司上单调递增,故 ,故 正确;因为 ,所以
,故D正确.故选BCD.
11.AD【解析】设三角形的斜边长为 ,则 ①,所以
为锐角,故 不呈周期变化,故 错误;对于 ,当
时,由①式得, ,所以 ,故A正确;对于
B,由①可得 ,故 ,且
,即 的图象关于直线
对称,故 错误;对于D, ,因为 ,当且仅当
时,等号成立,又由①可得, ,所以
,所以 ,所以
,所以 ,所以 ,所以
,即 ,故D正确.故选AD.
三、填空题
12.存在能被4整除的正整数不能被2整除.
【解析】“所有能被4整除的正整数都能被2整除”是全称量词命题,其否定是存在量词命题,所以“所
有能被4整除的正整数都能被2整除”的否定是:“存在能被4整除的正整数不能被2整除”.故答案为
存在能被4整除的正整数不能被2整除.
学科网(北京)股份有限公司13.
【解析】将 的图象向左平移 个单位长度,得到函数
的图象,若 与曲
线 关于原点对称,可得 ,即
,可得 ,由于
不恒等于0,所以 ,故 .故答案为 .
14. 【解析】设函数 ,则 ,所以
在 上单调递增.所以
.设
,则 ,由
;由 .所以 在 上单调递增,
在 上单调递减, ,且 ,故
.故答案为 .
四、解答题
学科网(北京)股份有限公司15.解:(1)在 中,由 ,
即 ,
化简得 ,又 ,所以 .
(2)由 ,解得 ,
由余弦定理变形可得
故 的周长为 .
16.解:(1)令 ,
解得 ,
所以 的单调递减区间为 .
(2)
所以 ,设 ,则 ,
故 ,
所以
学科网(北京)股份有限公司当且仅当 ,即 或 时等号成立,故 的最大值为0.
17.解:(1)由条件及正弦定理得 ,
所以 ,而 ,
则 ,
即 ,
,
因此 或 (舍去).
(2)在 中,由正弦定理得 ①.
在 中,由正弦定理得 ②.
且 ,
由①②可得,
解得 .
18.解:(1)因为 ,则
令 得 或 ,
当 与 时, ;
当 时, ;故 的单调增区间为 ,单调减区间为 .
(2)由(1)得 ,则直线 的方程为
即 ,
学科网(北京)股份有限公司由 ,
得 ,
设 ,
则 ,
令 得 ,当 时, ;
当 时, ;所以 在 单调递减,在 单调递增,
因为 ,存在唯一的 ,使
,所以 有且仅有2个零点 ,其中 ,这表明方程
0的解集为 ,
即直线 与曲线 交于另一点 ,且 的横坐标为 .
19.解:(1)设函数 ,其中 ,则 ,
令 ,其中 ,
所以, ,
所以 在 上单调递增,故 ,
所以 在( 上单调递增,则 ,即 .
(2)由题意可得
因为 ,则 ,
由(1)可得,
学科网(北京)股份有限公司所以 ,
因为 ,
所以
所以对任意的 ,
故函数 在 上单调递减,无最小值.
学科网(北京)股份有限公司