重庆市主城区2024届高三下学期第二次学业质量抽测数学试题_2024年4月_01按日期_22号_2024届重庆主城高三学业质量调研抽测（第二次）

高 2024 届学业质量调研抽测（第二次） 数学试卷 本卷满分 150 分，考试时间 120 分钟。 注意事项： 1．答卷前，考生务必将自己的姓名、准考证号等填写在答题卡和试卷指定位置上。 2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。如需改动，用橡 皮擦干净后，再选涂其他答案标号。回答非选择题时，将答案写在答题卡上。写在本试卷上无效。 一、选择题：本大题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目 要求的。（ ） 1.设集合A x| y ln(2x) ，B   x|x23x40  ，则下列结论正确的是（ ） A.AB R B.AB  C.Bð A D.A ð B (1,2) R R z 2 2.已知复数z满足 2i，则复数z在复平面内的对应点在（ ） z1 A.第一象限 B.第二象限 C.第三象限 D.第四象限 3.设S 为正项等比数列 a 的前n项和，已知a 2，S a 2，则a 的值为（ ） n n 1 4 5 10 A.20 B.512 C.1024 D.2048 4.民间娱乐健身工具陀螺起源于我国，最早出土的石制陀螺在山西夏县的新石器时代遗址中发现.如图，是 一个陀螺的立体结构图（上端是圆柱，下端是圆锥），已知底面圆的直径AB 8，圆柱体部分的高BC 5， 圆锥体部分的高CD 3，则这个陀螺的表面积为（ ） A.60 B.76 C.92 D.96 5.过抛物线 y2 8x焦点F 的直线交该抛物线于点M ，N ，已知点M 在第一象限，过M 作该抛物线准线 的垂线，垂足为Q，若直线QF 的倾斜角为120，则|MN |的长度为（ ） 20 26 32 34 A. B. C. D. 3 3 3 3 Ck 6.有一组样本数据0，1，2，3，4，添加一个数X 形成一组新的数据，且P(X k) 4 (k{0,1,2,3,4})， 16 学学学科科科网网网（（（北北北京京京）））股股股份份份有有有限限限公公公司司司则新的样本数据的第25百分位数不变的概率为（ ） 1 5 11 15 A. B. C. D. 16 16 16 16     7.在△ABC中，角A，B，C所对的边分别为a，b，c，已知sinBsinC    cosBsinC   ，  6  3 21 b2，sinB  .则a的值为（ ） 7 7 21 A. 7 B. C. D. 21 2 3 8.已知函数 y  f (x)的定义域是(,0)(0,)，对任意的x ，x (0,)，x  x ，都有 1 2 1 2 x f  x x f  x  2 2 1 1 0，若函数 y  f (x1)的图象关于点(1,0)成中心对称，且 f(1)4，则不等式 x x 2 1 4 f(x) 的解集为（ ） x A.(1,0)(0,1) B.(1,0)(1,) C.(,1)(0,1) D.(,1)(1,) 二、选择题：本大题共 3小题，每小题6分，共18分.在每小题给出的四个选项中，有多项符 合题目要求，全部选对的得6分，部分选对的得部分分，有选错的得0分。 9.若bc1，0a1，则下列结论正确的是（ ） A.ba ca B.log a log a C.cba bca D.blog a clog a b c c b    5 10.已知函数 f(x)3sin(2x)   的图象关于直线x 对称，则下列说法正确的是  2 2 12 （ ）  A. 6  7 B. f x  为偶函数  12    C. f(x)在  ,  上单调递增 4 2  D.若 f  x  f  x   6，则 x x 的最小值为 1 2 1 2 2 x2 y2 11.已知F ，F 是双曲线  1(a0,b0)的左、右焦点，且 FF 4，点P是双曲线上位于第一 1 2 a2 b2 1 2 象限内的动点，FPF 的平分线交x轴于点M ，过点F 作F E垂直于PM 于点E.则下列说法正确的是 1 2 2 2 学学学科科科网网网（（（北北北京京京）））股股股份份份有有有限限限公公公司司司（ ） A.若点F 到双曲线的渐近线的距离为 3，则双曲线的离心率为2 2 B.当FPF 60时，△FPF 面积为4 3 1 2 1 2 C.当 PF 3a时，点M 的坐标为(1,0) 1 2 35 D.若 FE  11b ，则0a 1 7 三、填空题：本大题共3小题，每小题5分，共15分。 12.在平面直角坐标系xOy中，已知点M(1,0)，N(5,3)，P是直线4x3y120上任意一点，则   OPMN ______. 13.有4人到甲、乙、丙三所学校去应聘，若每人至多被一所学校录用，每所学校至少录用其中1人，则所 有不同的录用情况种数为______.（用数字作答） 14.若函数 f(x)在定义域内存在x  x 0 使得 f x f  x ，则称 f(x)为“函数”，x 为该函 0 0 0 0 0 x2ln2,x0  数的一个“点”.设g(x) ，若ln2是g(x)的一个“点”，则实数a的值为______； ln  aex ,x0  若g(x)为“函数”，则实数a的取值范围是______. 四、解答题：本大题共5小题，共77分。解答应写出文字说明、证明过程或演算步骤。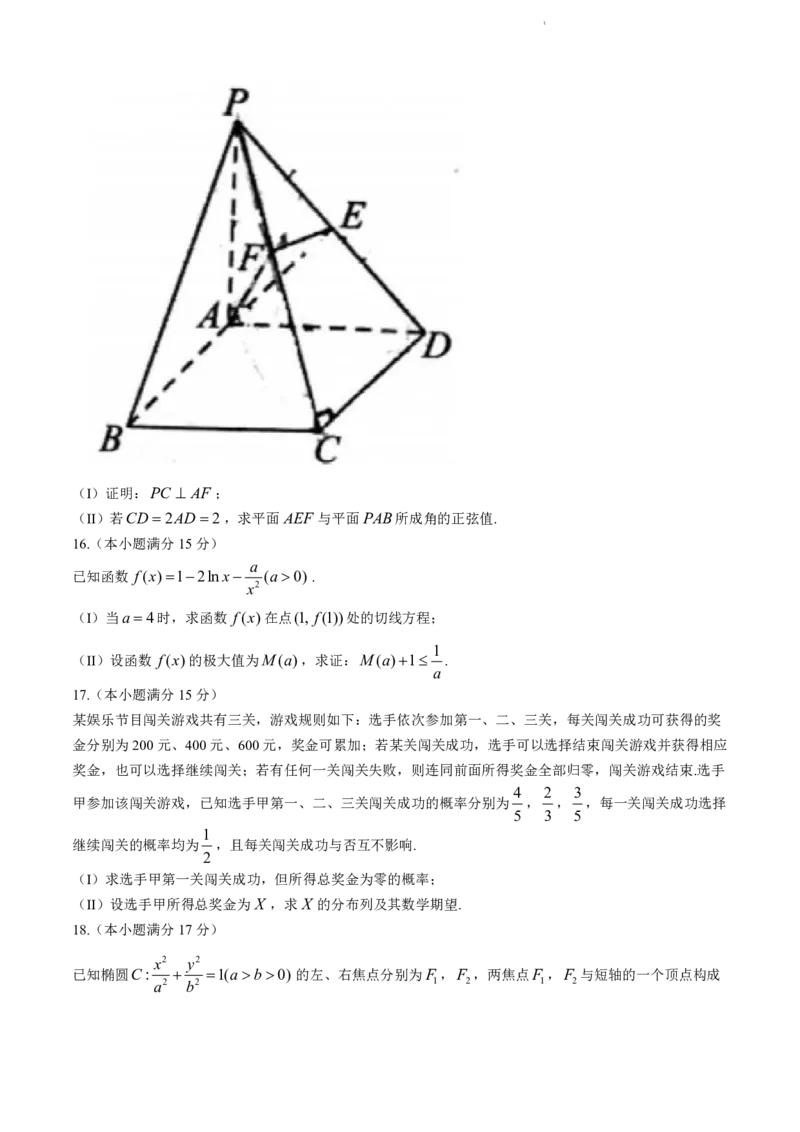 15.（本小题满分13分） 如图，在四棱锥PABCD中，PA平面ABCD，四边形ABCD是矩形，PA AD，过棱PD的中点E 作EF PC 于点F ，连接AF . 学学学科科科网网网（（（北北北京京京）））股股股份份份有有有限限限公公公司司司（I）证明：PC  AF ； （II）若CD 2AD 2，求平面AEF 与平面PAB所成角的正弦值. 16.（本小题满分15分） a 已知函数 f(x)12lnx (a 0) . x2 （I）当a 4时，求函数 f(x)在点(1, f(1))处的切线方程； 1 （II）设函数 f(x)的极大值为M(a)，求证：M(a)1 . a 17.（本小题满分15分） 某娱乐节目闯关游戏共有三关，游戏规则如下：选手依次参加第一、二、三关，每关闯关成功可获得的奖 金分别为200元、400元、600元，奖金可累加；若某关闯关成功，选手可以选择结束闯关游戏并获得相应 奖金，也可以选择继续闯关；若有任何一关闯关失败，则连同前面所得奖金全部归零，闯关游戏结束.选手 4 2 3 甲参加该闯关游戏，已知选手甲第一、二、三关闯关成功的概率分别为 ， ， ，每一关闯关成功选择 5 3 5 1 继续闯关的概率均为 ，且每关闯关成功与否互不影响. 2 （I）求选手甲第一关闯关成功，但所得总奖金为零的概率； （II）设选手甲所得总奖金为X ，求X 的分布列及其数学期望. 18.（本小题满分17分） x2 y2 已知椭圆C:  1(a b 0) 的左、右焦点分别为F ，F ，两焦点F ，F 与短轴的一个顶点构成 a2 b2 1 2 1 2 学学学科科科网网网（（（北北北京京京）））股股股份份份有有有限限限公公公司司司 6 等边三角形，点P 2, 在椭圆C上.   2   （I）求椭圆C的标准方程； （II）过点F 且斜率不为0的直线l与椭圆C交于A，B两点，与直线x3交于点D. 1 ①设△ABF 内切圆的圆心为I ，求tanIAB的最大值； 2     ②设AD AF ，BD BF ，证明：为定值. 1 1 2 1 1 2 19.（本小题满分17分） 高斯是德国著名的数学家，近代数学的奠基者之一，享有“数学王子”的称号，用其名字命名的“高斯函 数”定义为：对于任意实数x，记[x]表示不超过x的最大整数，则y [x]称为“高斯函数”.例如： y [3.5]4， y [2.1]2.  1 1 （I）设 f(x)[x]  x  [2x]，xR，求证： 是 f(x)的一个周期，且 f(x)0恒成立；  2 2 （II）已知数列 a 的通项公式为a  1  1  1  1  n N* ，设 n n n2 n2 1 n2 2 n2 2n b    1     1  1   nN* . n a  a 2 n n 2 ①求证：n n1； a n 1 1 1  ②求    的值. b b b  1 2 2024 学学学科科科网网网（（（北北北京京京）））股股股份份份有有有限限限公公公司司司