文档内容
2023 年下学期期中考试试卷
高三数学
本试卷分为问卷和答卷.考试时量120分钟,满分150分.请将答案写在答题卡上.
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一个选
项是符合题目要求的.
1. 已知集合 , ,则 ( )
A. B. C. D.
2. 已知 ,若复数 为纯虚数,则复数 在复平面内对应的点所在的象限为
( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
3. 若向量 ,则“ ”是“向量 的夹角为钝角”的( )
A. 充分不必要条件 B. 必要不充分条件
.
C 充要条件 D. 既不充分也不必要条件
4. 设等差数列 的公差为 ,前 项和为 ,若 ,且 ,则 ( )
.
A B. C. 1 D. 3
5. 已知某种垃圾的分解率为 ,与时间 (月)满足函数关系式 (其中 , 为非零常数),若经
过12个月,这种垃圾的分解率为10%,经过24个月,这种垃圾的分解率为20%,那么这种垃圾完全分解,
至少需要经过( )(参考数据: )
A. 48个月 B. 52个月 C. 64个月 D. 120个月
6. 已知函数 的部分图象如图所示,其中 .在已知 的条件
下,则下列选项中可以确定其值的量为( )
第1页/共6页
学科网(北京)股份有限公司A. B. C. D.
7. 已知向量 满足 ,且 ,则 ( )
A. B. C. D.
8. 已知函数 ,当 时, 恒成立,则m的取值范围为( )
A. B. C. D.
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目
要求.全部选对得5分,部分选对得2分,有选错的得0分.
的
9. 关于函数 ,下列结论正确 是( )
A. 的最小正周期为 B. 的最大值为2
C. 在 上单调递减 D. 是 的一条对称轴
10. 设等比数列 的公比为 ,其前n项和为 ,前n项积为 ,并满足 , ,
,下列结论正确的有( )
A. B.
第2页/共6页
学科网(北京)股份有限公司C. 是数列 中的最大项 D. 是数列 中的最大项
11. 已知过抛物线T: 的焦点F的直线l交抛物线T于A,B两点,交抛物线T的准线与点
M, , ,则下列说法正确的有( )
A. 直线l的倾斜角为150° B.
的
C. 点F到准线 距离为8 D. 抛物线T的方程为
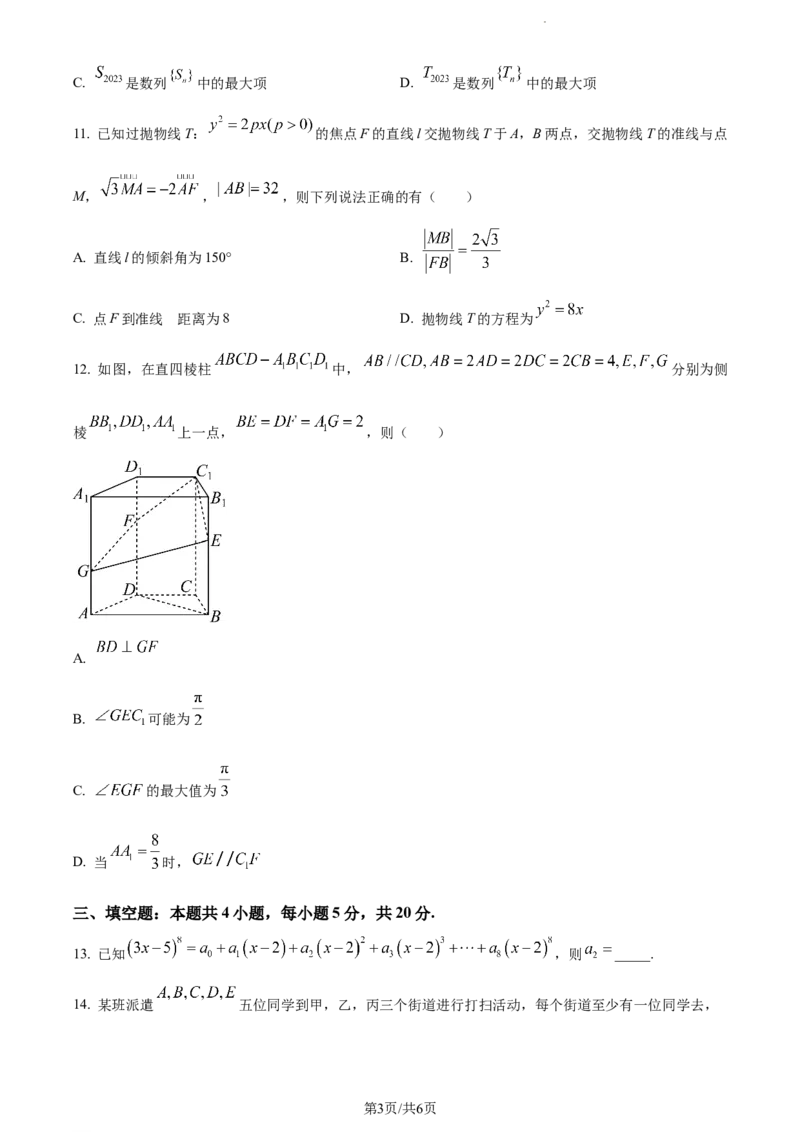
12. 如图,在直四棱柱 中, 分别为侧
棱 上一点, ,则( )
A.
B. 可能为
C. 的最大值为
D. 当 时,
三、填空题:本题共4小题,每小题5分,共20分.
13. 已知 ,则 _____.
14. 某班派遣 五位同学到甲,乙,丙三个街道进行打扫活动,每个街道至少有一位同学去,
第3页/共6页
学科网(北京)股份有限公司至多有两位同学去,且 两位同学去同一个街道,则不同的派遣方法有_________种.
15. 已知体积为96的四棱锥 的底面是边长为 的正方形,底面ABCD的中心为 ,四棱锥
的外接球球心O到底面ABCD的距离为2,则点P的轨迹的长度为_________.
16. 已知函数 有两个极值点 ,且 ,则实数m的取值范围是__________.
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17. 已知数列 满足
(1)令 ,求证:数列 为等比数列;
(2)求数列 的前 项和为 .
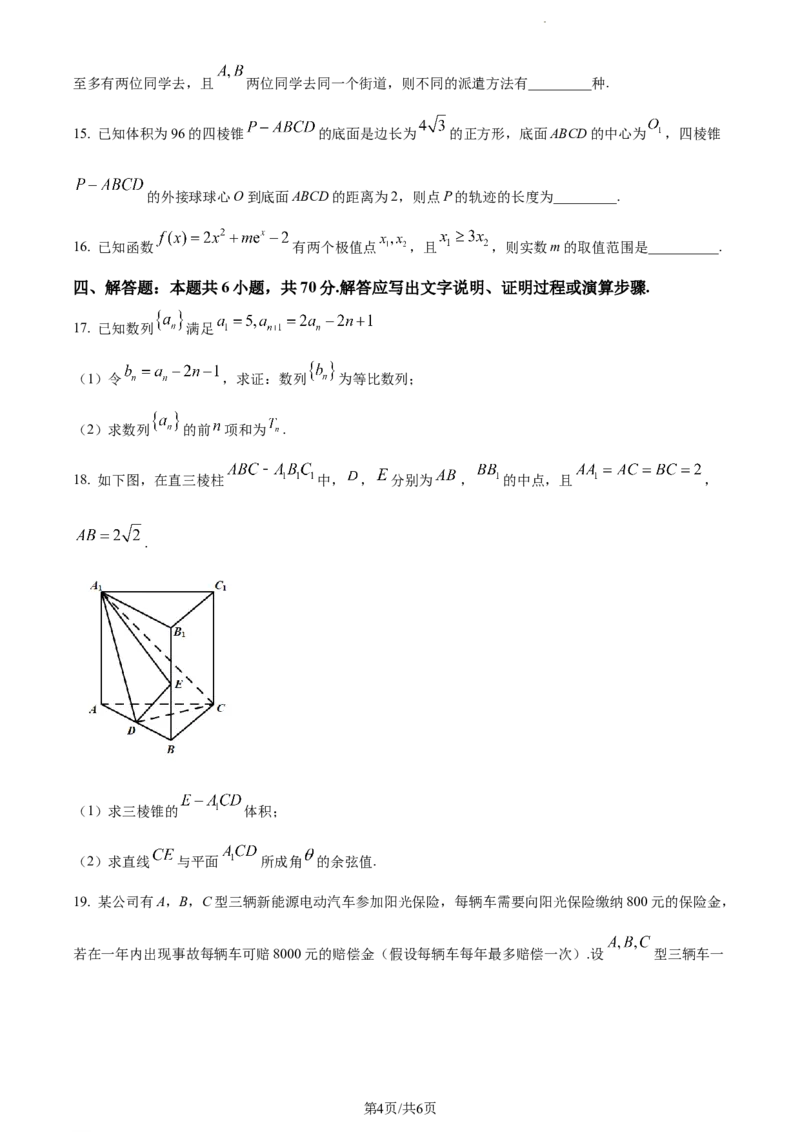
18. 如下图,在直三棱柱 中, , 分别为 , 的中点,且 ,
.
(1)求三棱锥的 体积;
(2)求直线 与平面 所成角 的余弦值.
19. 某公司有A,B,C型三辆新能源电动汽车参加阳光保险,每辆车需要向阳光保险缴纳800元的保险金,
若在一年内出现事故每辆车可赔8000元的赔偿金(假设每辆车每年最多赔偿一次).设 型三辆车一
第4页/共6页
学科网(北京)股份有限公司年内发生事故的概率分别为 , , ,且每辆车是否发生事故相互独立.
(1)求该公司获赔的概率;
(2)设获赔金额为X,求X的分布列和数学期望.
20. 在 中,a、b、c分别为角 所对的三边,若
(1)求角C;
(2)若 ,求 的最大值.
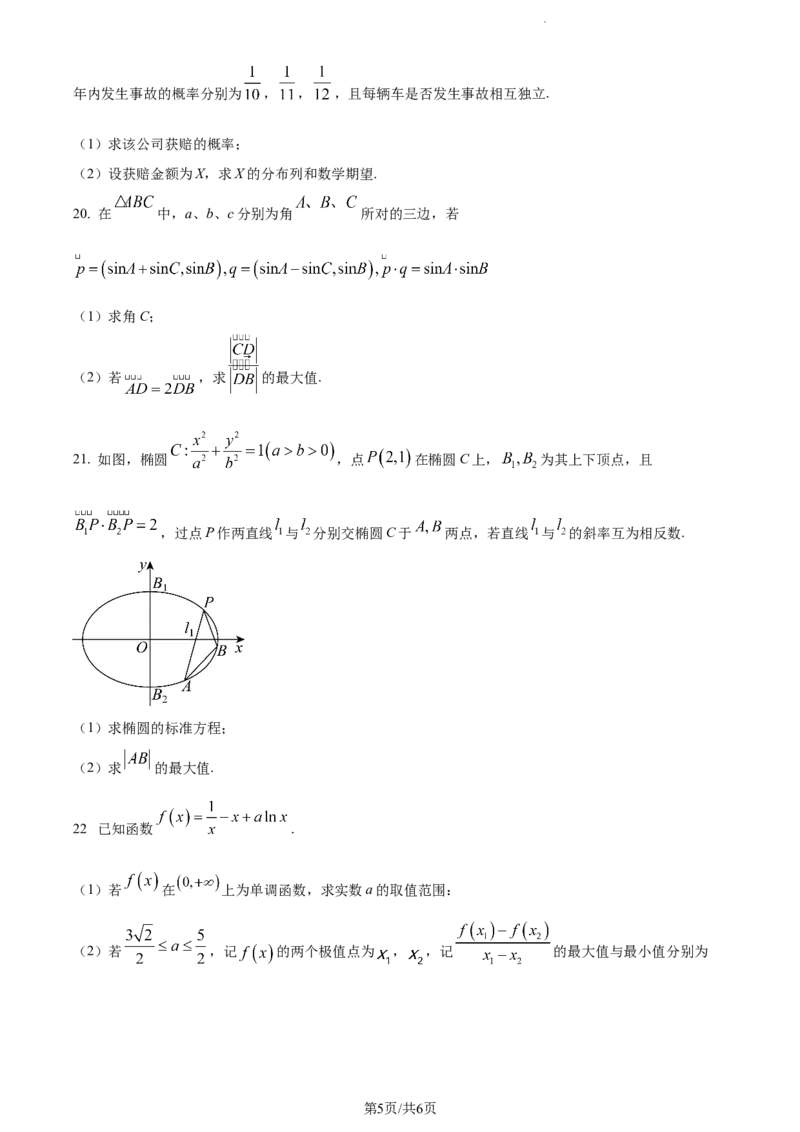
21. 如图,椭圆 ,点 在椭圆C上, 为其上下顶点,且
,过点P作两直线 与 分别交椭圆C于 两点,若直线 与 的斜率互为相反数.
(1)求椭圆的标准方程;
(2)求 的最大值.
.
22 已知函数 .
(1)若 在 上为单调函数,求实数a的取值范围:
(2)若 ,记 的两个极值点为 , ,记 的最大值与最小值分别为
第5页/共6页
学科网(北京)股份有限公司M,m,求 的值.
第6页/共6页
学科网(北京)股份有限公司